Задача 1
В группе из 15 человек 8 человек занимается спортом. Найти вероятность того, что из случайно выбранных 6 человек 5 человек занимаются спортом.
Решение
Найдем число сочетаний по 8 человек из 15:
![]()
![]() - число сочетаний из
15 по 8
- число сочетаний из
15 по 8
Пусть А0 – {среди 6 человек нет занимающихся спортом}
А1 – {среди 6 человек 1 занимается спортом}
А2 – {среди 6 человек 2 занимаются спортом}
А3 – {среди 6 человек 3 занимаются спортом}
А4 – {среди 6 человек 4 занимаются спортом}
А5 – {среди 6 человек 5 занимаются спортом}
Тогда событие А = {6 человек из 5 занимаются спортом} можно
представить в виде: ![]() . Так как эти события несовместны, то
. Так как эти события несовместны, то ![]() .
.
Отобрать 6 человек из 15 можно 6435 способами (см. выше).
Событию ![]() благоприятствует
благоприятствует ![]() случаев.
Следовательно,
случаев.
Следовательно, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Задача 2
Найти вероятность того, что дни рождения 12 человек будут в разные месяцы года.
Решение
Т.к. в году 12 месяцев, то вероятность рождения в каждом месяце будет равна p=1/12.
Задача 3
На одной полке наудачу расставляется 15 книг. Найти вероятность того, что определенные 3 книги окажутся поставленными рядом.
Решение
Вероятность того, что каждая из 15 книг окажется на определенном месте, равна 1/15. Найдем число сочетаний по 3 книги из 15
![]()
![]()
Так как порядок в тройках книг не важен, то возможное число троек книг равно 455 / 3 ≈ 151.
Следовательно, вероятность того, что 3 книги будут рядом равна 15/151≈0,0989
Задача 5
На каждой из семи одинаковых карточек написана одна из следующих букв: А, А, Е, Н, С, Т, Т. Карточки перемешаны. Определить вероятность того, что из вынутых и положенных в ряд карточек а) можно составить слово «СТЕНА»; б) из трех карточек можно составить слово «НЕТ».
Решение
Найдем сколько можно составить 5-ти буквенных слов из 7 букв:
![]()
![]() - количество
5-тибуквенных комбинаций
- количество
5-тибуквенных комбинаций
Так как слово «СТЕНА» можно составить единственным способом, то вероятность Р этого события = 1/21.
Теперь найдем число комбинаций 3 букв из 7:
![]() - количество
3-хбуквенных комбинаций
- количество
3-хбуквенных комбинаций
Так как слово «НЕТ» составляется только одним способом, то вероятность Р этого событии – 1/35.
Задача 7
Найти вероятность того, что наудачу взятое двухзначное число кратно трем или пяти.
Решение
Всего есть 90 двухзначных чисел.
Перечислим двухзначные числа кратные трем или пяти; 10, 12, 15, 18, 20, 21, 24, 25, 27, 30, 33, 35, 36, 39, 40, 42, 45, 48, 50, 51, 54, 55, 57, 60, 63, 65, 66, 69, 70, 72, 75, 78, 80, 81, 84, 85, 87, 90, 93, 95, 96, 99.
Всего 42 двухзначных чисел, которые делятся на 3 или на 5.
Следовательно, вероятность того, что взятое двухзначное число кратно 3 или 5 равна Р = 42 / 90 = 7/15.
Задача 9
В первом ящике из 6 шаров 4 красных и 2 черных, во втором ящике из 7 шаров 2 красных и 5 черных. Из первого ящика во второй переложили один шар, затем из второго в первый переложили один шар. Найти вероятность того, что шар, извлеченный после этого из первого ящика будет черным.
Решение
Всего имеется 6 красных и 7 черных шаров. Т.е. всего 13 шаров.
Вероятность извлечения черного шара из 1-го ящика = ![]()
После перекладывания из первого во второй, вероятность
извлечения черного шара из второго ящика = ![]()
Следовательно, после перекладывания шара из второго ящика в
первый, вероятность извлечения черного шара = ![]()
Задача 11
В семье 10 детей. Считая вероятность рождения девочки и мальчика равными 0,5, определить вероятность того, что в данной семье: а) пять мальчиков; б) мальчиков не менее трех, но не более восьми.
Решение
а) вероятность того, что в семье 5 мальчиков = 5 / 10 = 0,5
б) вероятность рождения 3-х мальчиков = 3 / 10 = 0,3
вероятность рождения 4-х мальчиков = 4 / 10 = 0,4
вероятность рождения 5-ти мальчиков = 5 / 10 = 0,5
вероятность рождения 6-ти мальчиков = 6 / 10 = 0,6
вероятность рождения 7-и мальчиков = 7 / 10 = 0,7
вероятность рождения 8-и мальчиков = 8 / 10 = 0,8
Следовательно, вероятность рождения от 3-х до 8-ми мальчиков составляет:
0,3 × 0,4 × 0,5 × 0,6 × 0,7 × 0,8 = 0,,02016
Задача 13
В автопарке 100 машин. Вероятность поломки машины равна 0,2. Найти наивероятнейшее число исправных автомобилей и вероятность этого числа.
Решение
Вероятное число поломанных машин = 100 × 0,2 = 20
Наивероятнейшее число исправных автомобилей = 100 – 20 = 80
Вероятность числа исправных автомобилей = 80 / 100 = 0,8
Задача 15
Вероятность работы каждого из 4 комбайнов без поломки в
течение определенного времени равна 0,9. Составить закон распределения
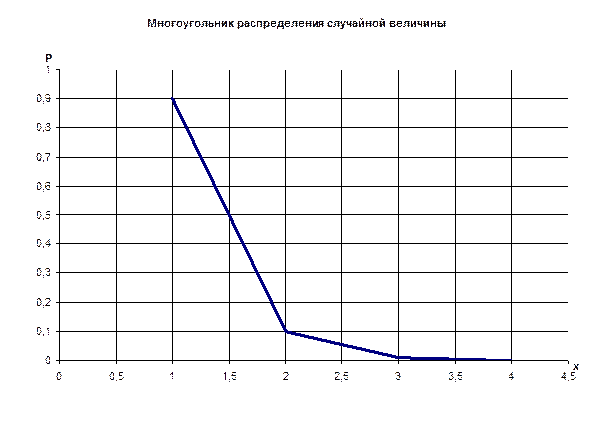
случайной величины Х – числа комбайнов, работавших безотказно. Построить
многоугольник распределения вероятностей, найти М(Х), D(X) и ![]() (х).
(х).
Решение
Вероятность
работы 4-х комбайнов = 1 - 0,9 / 4 = 0,225
работы 3-х комбайнов = 0,9 / 3 = 0,3
работы 2-х комбайнов = 0,9 / 2 = 0,45
работы 1-го комбайна = 1 – 0,45 – 0,3 – 0,225 = 0,025
Таким образом, ряд распределения случайной величины Х имеет вид
|
xi |
1 |
2 |
3 |
4 |
|
pi |
0,9 |
0,1*0,9=0,098 |
0,12*0,9=0,009 |
0,13*0,9=0,0009 |
Построим многоугольник распределения случайной величины:
120
Найдем математическое ожидание ![]() , дисперсию
, дисперсию ![]() и среднее квадратичное
отклонение
и среднее квадратичное
отклонение ![]()
![]()
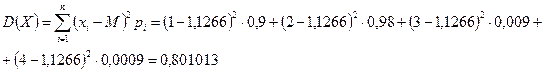
![]()
Задача 17
Х – нормально распределенная случайная величина с
параметрами ![]() и
и ![]() . Найти
. Найти ![]() ,
, ![]() .
.
Решение
Вероятность попадания нормально распределенной случайной
величины в заданный интервал ![]() определяется формулой
определяется формулой
![]() , где
, где ![]() - функция Лапласа
- функция Лапласа
1) 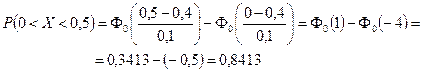
2) ![]()
Чтобы найти данную вероятность предварительно нужно найти
пределы случайной величины. Для этого решим неравенство ![]()
Возведем обе части неравенства в квадрат, получим ![]() =>
=> ![]() . Решив данное неравенство, получим интервал
. Решив данное неравенство, получим интервал ![]() .
.
Теперь найдем