Задача 2

Имеются следующие данные по предприятиям отрасли:

Предприятие	Среднегодовая стоимость основных производственных фондов млн. руб.	Объем произведенной продукции млн. руб.
1-е	3,5	2,5
2-е	1,0	1,6
3-е	4,0	2,8
4-е	4,9	4,4
5-е	7,0	10,9
6-е	2,3	2,8
7-е	6,6	10,2
8-е	2,0	2,5
9-е	4,7	3,5
10-е	5,6	8,9
11-е	4,2	3,2
12-е	3,0	3,2
13-е	6,1	9,6
14-е	2,0	3,5
15-е	3,9	4,2
16-е	3,8	4,4
17-е	3,3	4,3
18-е	3,0	2,4
19-е	3,1	3,2
20-е	4,5	7,9

Для получения зависимости между стоимостью основных производственных фондов и объемов продукции произведите группировку предприятий по стоимости основных производственных фондов, образовав четыре группы с равными интервалами. По каждой группе и в целом по совокупности посчитайте:

число предприятий;

стоимость основных производственных фондов – всего и в среднем на одно предприятие;

стоимость продукции – всего и в среднем на одно предприятие;

фондоотдачу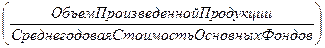

Результаты представьте в разработочной и групповой таблицах. Дайте анализ показателей таблицы и сделайте краткие выводы.

Решение

Минимальное значение: 1,0

Максимальное значение: 7,0

Размах: 7 – 1 = 6

Размах (интервал) одной группы: 6 / 4 = 1,5

Разработочная таблица распределения предприятий по группам стоимости основных производственных фондов

Интервалы групп	№ предприятия	Среднегодовая стоимость основных производственных фондов млн. руб.	Объем произведенной продукции млн. руб.
1 – 2,5	2	1	1,6
6	2,3	2,8
8	2	2,5
14	2	3,5
Итого первая группа	4 предприятия	7,3	10,4
Среднее по 1-ой группе		1,825	2,6
2,5 – 4,0	1	3,5	2,5
3	4	2,8
12	3	3,2
15	3,9	4,2
16	3,8	4,4
17	3,3	4,3
18	3	2,4
19	3,1	3,2
Итого вторая группа		27,6	27
Среднее по 2-ой группе	8 предприятий	3,45	3,375
4,0 – 5,5	4	4,9	4,4
9	4,7	3,5
11	4,2	3,2
20	4,5	7,9
Итого третья группа	4 предприятия	18,3	19
Среднее по 3-ой группе		4,575	4,75
5,5 – 7,0	5	7	10,9
7	6,6	10,2
10	5,6	8,9
13	6,1	9,6
Итого 4-ая группа	4 предприятия	25,3	39,6
Среднее по 4-ой группе		6,325	9,9
Итого	20 предприятий	78,5	96

По каждой группе и в целом по совокупности подсчитаем:

1. Число предприятий

Группа 1 – 2,5: 4

Группа 2,5 – 4,0: 8

Группа 4,0 – 5,5: 4

Группа 5,5 – 7,0: 4

В целом 20 предприятий

2. Стоимость продукции – всего и в среднем на одно предприятие:

Общая стоимость продукции

2,5 + 1,6 + 2,8 + 4,4 + 10,9 + 2,8 + 10,2 + 2,5 + 3,5 + 8,9 + 3,2 + 3,2 +

+9,6 + 3,5 + 4,2 + 4,4 + 4,3 + 2,4 + 3,2 + 7,9 = 96

Средняя стоимость продукции на одно предприятие

96 / 20 = 4,8

4. Фондоотдача

Фондоотдача = объем произведенной продукции /

среднегодовая стоимость основных фондов

Среднегодовая стоимость основных фондов:

3,5 + 1,0 + 4,0 + 4,9 + 7,0 + 2,3 + 6,6 + 2,0 + 4,7 + 5,6 + 4,2 +

+ 3,0 + 6,1 + 2,0 + 3,9 + 3,8 +3,3 + 3,0 + 3,1 + 4,5 = 78,5

Фондоотдача = 96 / 78,5 ≈ 1,223

Групповая таблица распределения предприятий по группам стоимости основных производственных фондов

Группа	Кол-во пред-й	Стоимость продукции	Стоимость основных фондов	Фондо-отдача
всего	в среднем на 1 пр-е	всего	в среднем на 1 пр-е
1	4	10,4	2,6	7,3	1,825	1,42465753
2	8	27	3,375	27,6	3,45	0,97826087
3	4	19	4,75	18,3	4,575	1,03825137
4	4	39,6	9,9	25,3	6,325	1,56521739
Всего:	20	96	4,8	78,5	3,925	5,00638716

Вывод: Большее число предприятия (8) попадает во вторую группу с интервалом 2,5 – 4,0 млн. руб. основных производственных фондов.

Задача 13

Производство однородной продукции предприятиями объединения составила:

Предприятие	Фактически произведено продукции млн.руб.	Выполнение плана, %	Удельный вес продукции первого сорта, %
1-е	41,2	103	85
2-е	20,9	95	80
3-е	32,1	107	90

Вычислить:

1) процент выполнения плана выпуска продукции в среднем по объединению;

2) средний процент выпуска продукции первого сорта по объединению.

Дать обоснование применения формул средних для расчета показателей. Сделать выводы.

Решение

1) Процент выполнения плана в среднем по объединению

1-е предприятие:

41,2 – 103%

х - 100% => х = 40

2-е предприятие:

20,9 – 95%

х - 100% => х = 22

3-е предприятие:

32,1 – 107%

х - 100% => х = 30

Средний процент выполнения плана по объединению

(40 + 22 + 30) / (41,2 + 20,9 + 32,1) × 100% ≈ 97,6%

2) Средний процент выпуска продукции первого сорта по объединению

(85*103 + 80*95 + 90*107) / (85 + 80 + 90) = 101,902

Выводы. В среднем по объединению план выполнен на 97,6%. Средний процент выпуска продукции первого сорта по объединению составляет 101,902%.

Задача 23

Данные об объеме розничного товарооборота на душу населения Новосибирской области:

Год	Продажа на душу населения, руб
1995	2974
1996	4496
1997	6902
1998	7932
1999	11031

Определить:

1) вид динамического ряда;

2) средний уровень динамического ряда;

3) абсолютные приросты, темпы роста и прироста, цепные и базисные, абсолютно содержание 1% прироста;

4) средний абсолютный прирост, средний темп роста и прироста уровней динамического ряда.

Результаты расчетов представьте в таблице. Изобразите динамический ряд на графике. Сделайте выводы.

Решение.

1. Вид динамического ряда: интервальный

2. Средний уровень ряда:

(2974 + 4496 + 6902 +7952 + 11031)/5 = 6667 млн. руб.

3. Рассчитаем абсолютные приросты, темпы роста и прироста (цепные и базисные), абсолютное содержание 1% прироста:

Абсолютным показателем анализа динамического ряда служит абсолютный прирост 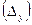, представляющий собой разность двух уровней ряда. Он может иметь положительный и отрицательный знак и измеряется в тех же единицах, что и уровни ряда:

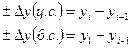например, для 1997 г.

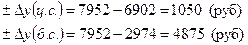
Результаты расчетов занесем в таблицу (графы 2 и 3)

За весь анализируемый период рассчитывается средний абсолютный прирост. Можно предложить две формулы, которые дают одинаковый результат:

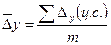или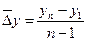

где m – число цепных абсолютных приростов, m = n - 1;

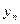- последний уровень динамического ряда

Среднегодовой абсолютный прирост продажи на душу населения равен:

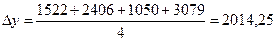(млн. руб.) или

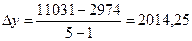(млн. руб.)

В среднем за год выпуск товаров и услуг увеличился на 2014,25 млн. руб.

Относительный показатель анализа ряда динамики – темп роста, выраженный в процентах 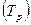или коэффициентах 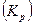представляет собой отношение двух уровней ряда:

, ,

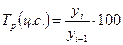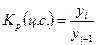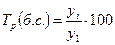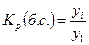Например, для 1996 г. он составил: к 1995 г.: ;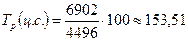

к 1994 г.: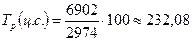

Результаты занесем в таблицу в графы 4, 5.

Между цепными и базисными темпами роста существует взаимосвязь: произведение последовательных цепных темпов роста (в коэффициентах) равно заключительному базисному темпу:

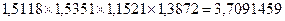
За весь анализируемый период рассчитывается средний (или среднегодовой) темп роста по формуле средней геометрической:

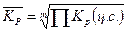, где

П – знак произведения;

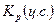- темп роста, исчисленный по цепной системе, в коэффициентах;

m – число цепных этапов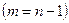

В нашем примере средний темп роста составил:

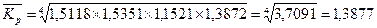или 138,77%

Так как произведение последовательных цепных темпов роста дает последний базисный, формула среднегодового темпа роста принимает вид:

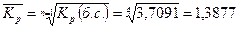или 138,77%

Наконец, расчет среднего темпа роста можно выполнить по исходным уровням ряда:

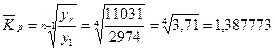или 138, 77%

Следующий показатель анализа ряда динамики – темп прироста (Тпр). Это – отношение абсолютного прироста к предыдущему или к базисному уровню, выраженному в процентах:

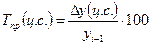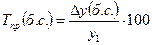
Темп прироста можно также рассчитать по данным о темпе роста, как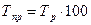

Для 1996 г. цепной темп прироста составил:

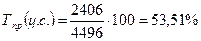или 153,51 – 100 = 53,51%

базисный темп прироста:

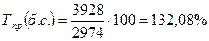или 132,08 – 100 = 32,08%

Результаты расчетов занесем в таблицу в графы 6 и 7.

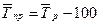, где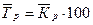

Среднегодовой темп прироста продажи на душу населения составил: 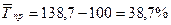, т.е. ежегодно уровни ряда возрастали в среднем на 38,7%.

В графе 8 таблицы рассчитаем содержание 1% прироста, показывающее, какая абсолютная величина скрывается за каждым процентом прироста. Оно определяется делением абсолютного прироста на соответствующий темп прироста (показатель исчисляется только по цепной системе):

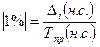или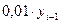

Например, для 1997 г. 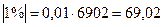(чел.)

Год	Продажа на душу населения, руб	Абсолютный прирост	Темп роста	Темп прироста	Значение 1% прироста
К предыду-щему году	К базисно-му году	К предыду-щему году	К базисно-му году	К предыду-щему году	К базисно-му году
А	1	2	3	4	5	6	7	8
1994	2974	Х	Х	Х	100	Х	Х	Х
1995	4496	1522	1522	151,18	151,18	150,18	51,18	29,74
1996	6902	2406	3928	153,51	232,08	152,51	132,08	44,96
1997	7952	1050	4978	115,21	267,38	114,21	167,38	69,02
1998	11031	3079	8057	138,72	370,91	137,72	270,91	79,52
Итого	33355	8057	18485	Х	Х	Х	Х	Х

Для наглядного изображения динамики построим линейную диаграмму. При построении диаграммы в прямоугольной системе координат на оси абсцисс будем откладывать периоды времени, а на оси ординат – уровни динамического ряда.

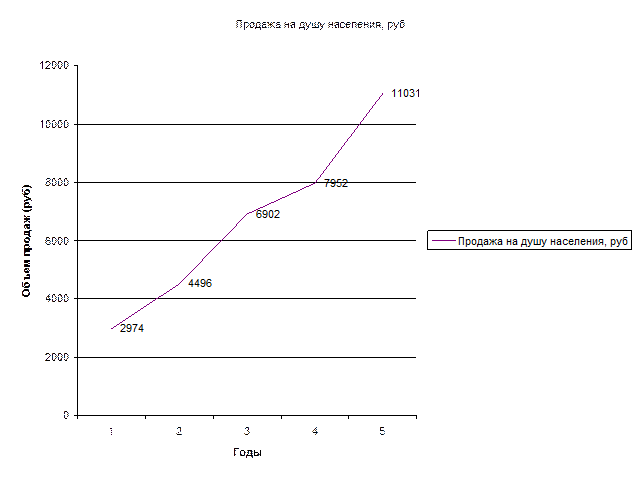
Анализируя исчисленные показатели, делаем вывод, что объем продаж на душу населения возрастает.

Задача 44

Производство продукции и ее себестоимости на предприятии за два периода составили:

Наименование продукции	Себестоимость единицы продукции, руб	Произведено продукции, тыс. шт.
Базисный период	отчетный период	базисный период	отчетный период
	Z₀	Z₁	q₀	q₁
А	82	105	121	97
Б	110	97	86	132
В	173	158	73	72

Определить:

1) индивидуальные индексы себестоимости и количества произведенной продукции;

2) общий индекс затрат на производство;

3) общий индекс себестоимости;

4) общий индекс физического объема произведенной продукции;

5) абсолютный размер изменения затрат производства – всего, в том числе за счет изменения себестоимости продукции и физического объема продукции

Показать взаимосвязь индексов. Сделать выводы.

Решение.

1. Взаимосвязь индексов себестоимости и количества произведенной продукции

себестоимость продукции «А»: 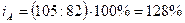, т.е. себестоимость продукции «А» увеличилась в отчетном периоде по сравнения с базисным на 28% или на 105-82=23 рубля;

количество продукции «А»: 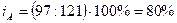, т.е. количество выпускаемой продукции «А» уменьшилось в отчетном периоде по сравнению с базисным на 20% или на 121-97=24 штуки;

себестоимость продукции «Б»: 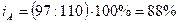, т.е. себестоимость продукции «Б» уменьшилась в отчетном периоде по сравнению с базисным на 12% или 110-97=13 рублей;

количество продукции «Б»: 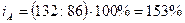, т.е. количество выпускаемой продукции «Б» увеличилось в отчетном периоде по сравнению с базисным на 53% или 132-86=46 штук;

себестоимость продукции «В»: 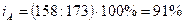, т.е. себестоимость продукции «В» уменьшилась в отчетном периоде по сравнению с базисным на 9% или 173 – 158 = 15 рублей;

количество продукции «В»: 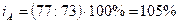, т.е. количество выпускаемой продукции «В» увеличилось в отчетном периоде по сравнению с базисным на 5% или 77-73=4 штуки.

2. Общий индекс затрат на производство

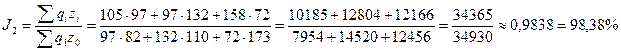
3. Общий индекс себестоимости

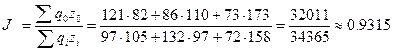Себестоимость всех видов продукции в отчетном периоде по сравнению с базисным увеличилась в 0,9315 раза или на 2354 тысячи рублей (34365 - 32011).

4. Общий индекс физического объема произведенной продукции

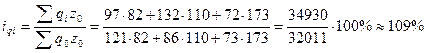Объем всех видов продукции в отчетном периоде по сравнении с базисным возрос на 9% или на 2919 тыс. штук.

5. Абсолютный размер изменения затрат производства:

всего: (105*97 + 97*132 + 158*77) – (82*121 + 110*86 + 173*73) = 3144

за счет изменения себестоимости: (105+97+158)/(82+110+173)=1,157556

за счет изменения объема: (97+132+72)/(121+86+77)=1,06

ВЫВОДЫ: Затраты на производство возросли преимущественно за счет изменения себестоимости.

Задача 76

Численность работников торговли сократилась на 5%, а средняя выработка возросла на 30%.

Определить, как изменился объем оборота. Привести формулы используемых индексов. Показать их взаимосвязь.

Решение

Оборот =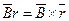

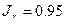
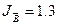
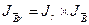= 0.95 × 1.3 = 1.235

ВЫВОД. Объем оборота возрос в 1.235 раза.

Задача 98

Имеются следующие данные об обороте розничной торговли и численности населения района, обслуживаемого потребительской кооперацией, за два года:

Показатели	Базисный год	Отчетный год
Оборот, млн. руб.	226,8	266,4
Среднегодовая численность обслуживаемого населения, тыс. чел.	36	37

Определить:

1) оборот на душу населения;

2) общую сумму прироста оборота в отчетном году по сравнению с базисным – всего, в том числе за счет изменения продажи на душу населения и численности населения;

3) долю прироста оборота за счет каждого фактора.

Сделать выводы.

Решение.

1) оборот на душу населения

в базисном году: 226800000 / 36000 = 6300 (руб / чел)

в отчетном году: 266400000 / 37000 = 7200 (руб / чел)

средний оборот: 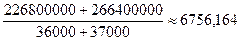(руб / чел)

2) сумма прироста оборота в отчетном году по сравнению с базисным

всего: 266400000 – 226800000 = 39600000 (руб)

за счет изменения продажи на душу:

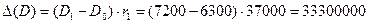
за счет изменения численности населения:

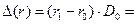(37000-36000)∙6300 = 6300000

3) доля прироста оборота за счет каждого фактора

за счет изменения продажи на душу населения: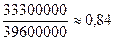

за счет изменения численности населения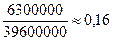

Выводы: Оборот на душу населения возрос, главным образом, за счет изменения продажи на душу населения.

Задача 116

Сведения об обороте, издержках обращения в действующих ценах и изменение цен на товары, тарифов и ставок на услуги торговой организации:

Показатели	Сумма, тыс.руб.	Индексы цен, тарифов и ставок
базисный период p₀q₀	отчетный период p₁q₁
Оборот	18408	22090	1,15
Издержки обращения	4050	5081	1,2

Рассчитать относительный уровень издержек обращения в отчетном и базисном периодах в действующих и сопоставимых ценах, тарифах и ставках. Разложить абсолютное изменение суммы издержек по факторам: за счет динамики физического объема оборота, уровня издержек и цен, тарифов, ставок.

Решение.

Относительный уровень издержек обращения:

- в действующих ценах в базисном периоде

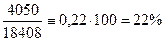
- в действующих ценах в отчетном периоде:

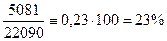
Относительный уровень издержек в сопоставимых ценах:

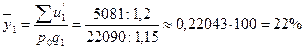
Разложение абсолютного изменения суммы издержек по факторам:

- общее изменение оборота

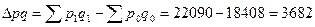
- за счет динамики физического объема оборота

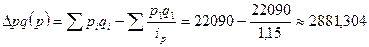
- за счет изменения издержек обращения

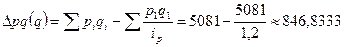
- за счет изменения цен, тарифов и ставок

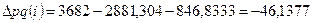
Задача 66

Данные о численности работников университета, начавшего свою работу 22 января (чел):

Число месяца	Списочная численность	Явочная численность
А	1	2
Январь
22	65	65
23	65	63
24	67	63
25	68	65
26	68	66
27	68	67
29	70	68
30	69	69
31	70	66
Март
1	72	70
2	72	70
3	71	68
5	71	67
6	70	67
7	69	68
9	69	65
10	70	68
12	70	69
13	73	70
14	73	71
15	73	71
16	73	73
17	72	70
19	72	72
20	72	71
21	73	70
22	73	72
23	72	71
24	72	69
26	71	70
27	71	69
28	71	68
29	71	70
30	69	66
31	69	67

Рассчитать:

1) среднеявочную численность работников за январь и март

2) среднесписочную численность работников за январь, март и за первый квартал

Решение

1) Среднеявочную численность работников найдем как среднее арифметическое.

За январь (65 + 63 + 63 + 65 + 66 + 67 + 68 + 69 + 66) / 9 = 592 / 9 ≈ 65, 78

За март (70 + 70 + 68 + 67 + 67 + 68 + 65 + 68 + 69 + 70 + 71 + 71 + 73 + 70 + 72 + 71 + 70 + 72 + 71 + 69 + 70 + 69 + 68 + 70 + 66 + 67) / 31 = 58,13

2) Среднесписочная численность за январь:

(65 + 65 + 67 + 68 + 68 + 68 + 70 + 69 + 70) / 31 = 19,67742 ≈ 19,7

Среднесписочная численность за март:

(72 + 72 + 71 +71 + 70 + 69 + 69 + 70 + 70 + 73 + 73 + 73 + 73 + 72 + 72 +

+ 72 + 73 + 73 + 72 + 72 + 71 + 71 + 71 + 71 + 69 + 69) / 31 =

= 59,80645 ≈ 60

Среднесписочная численность за 1 квартал:

(19,7 + 64 + 60) / 3 = 47,9