Министерство общего и
профессионального образования
Российской Федерации
Южно-Уральский
Государственный Университет
Кафедра АиУ.
Реферат
по математическим
основам теории систем
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ
АЛГЕБРЫ И МАТРИЧНОГО МНОЖЕСТВА
Выполнил: Подрезов Сергей
Валерьевич
Группа: ПС-243
Преподаватель: Разнополов Олег
Александрович
Челябинск, 2005
Содержание.
Содержание. 2
1. Введение. 3
2.
Основные понятия. 3
1.1. Основные типы матриц. 3
1.2. Простейшие операции над матрицами. 4
2. Определители. 5
2.1. Миноры и алгебраические дополнения. 6
2.2. Союзная и обратная матрицы. 6
3. Вектор. Линейное пространство. 7
3.1. Линейное пространство. 8
3.2. Правило Крамера для решения
линейных уравнений. 8
3.3. Однородная система уравнений. 8
4. Собственные числа. 9
4.1. Характеристическое уравнение. 9
5. Билинейная и квадратичная форма. 9
6. Матричные многочлены. 9
7. Функциональное пространство. 11
8. Метрическое пространство. 12
Заключение. 14
Используемая литература. 14
1.
Введение.
Одной из важнейших задач математики является исследование и
решение систем уравнений первой степени. Как само существование решений
системы, так и возможные числовые значения элементов решения полностью
определяются матрицами. В реферате я рассмотрел некоторые общие вопросы, касающиеся
матриц:
Þ
определители квадратных матриц второго,
третьего и высших порядков;
Þ
минор матрицы;
Þ
ранг матрицы;
Þ
операции над матрицами;
Þ
собственные числа;
Þ
функциональное пространство.
2. Основные понятия.
Система линейных уравнений
а11х1 + а12х2 + а13х3 +…+ а1nхn = у1
а21х1 + а22х2 + а23х3 +…+ а2nхn = у2
…………………………………………………………
аm1х1 + аm2х2 + аm3х3 +…+ аmnхn = уm
будет некоторое множество связей между переменными х1, х2,…,хn и у1, у2,…, уm. Эти связи, или
линейное преобразование переменных х в
переменные у, полностью характеризуются
упорядоченным набором коэффициентов aij. Если это множество коэффициентов обозначить через A и записать в виде
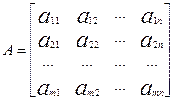 ,
,
то, как будет показано, посредством введения определения
«произведение Ах» систему линейных уравнений можно записать в виде: Ах = у.
Несомненно, приведенное выражение по виду значительно проще, чем соответствующая
система линейных уравнений. Это одна из соответствующих причин использования
матриц.
Столбцы
матриц называются векторами-столбцами,
а строки матрицы - векторами-строками.
Матрица, содержащая m строк и n столбцов,
называется (m×n) матрицей.
Квадратная матрица (m = n), является
матрица n-го
порядка.
1.1. Основные
типы матриц.
·
Матрица типа (m×1)
называется матрицей-столбцом или вектором-столбцом, т.к. она состоит из
одного столбца и m строк.

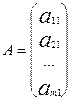 .
.
·
Матрица типа (1×n),
содержащая одну строку элементов, называется матрицей строкой.
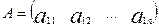 .
.
·
Диагональной
матрицей называется квадратная матрица, элементы которой, не лежащие на
главной диагонали, равны нулю.
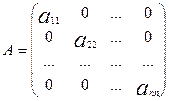 .
.
·
Единичной
матрицей называется диагональная матрица, диагональные элементы которой
равны единице.
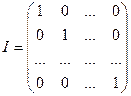 .
.
·
Транспонирование
матрицы А – операция, при которой ее строки и столбцы меняются местами (Ат).
·
Матрица, все элементы которой тождественно равны
нулю, называется нулевой матрицей.
1.2. Простейшие
операции над матрицами.
Если матрицы А и В одного порядка
(m×n), то
суммой служит матрица С = А + В, элемент которой определяется как cij = aij + bij, 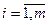 ;
; 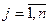 .
.
Свойства: А + В = В + А (коммутативность);
А + (В + С) =
(А + В) + С (ассоциативность).
Разность матриц одного порядка (m×n) равна
матрице D = А – В,
элементы которой определяются как: dij = aij - bij, 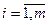 ;
; 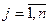 .
.
- Матрицы
А и В одинакового порядка равны, если равны их соответствующие элементы: a =
b.
- Произведение матриц.
Произведение матриц А и В может
рассматриваться как матрица С, где С = АВ, или [Сik] = [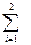 aijbjk]. В общем случае: С
= АВ = [
aijbjk]. В общем случае: С
= АВ = [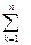 aikbjk].
aikbjk].
Если число столбцов матрицы А
равно числу строк матрицы В, то матрицы А и В согласованы по форме, а если
матрицы А и В равны (А = В), т.е. АВ = ВА, то говорят, что эти матрицы
коммутативны.
- Умножение матриц на скалярную величину.
При левом или правом умножении
матрицы на скалярную величину R, каждый элемент данной
матрицы умножается на этот скаляр R. Произвольный элемент
произведения RA равен Raij.
- Умножение транспонированных матриц.
ВтАт
= (АВ)т.
В общем случае: Ст =
(АВ)т = ВтАт.
- Дифференцирование матриц.
Производная от А(t) по переменной t определяется как:
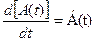 =
=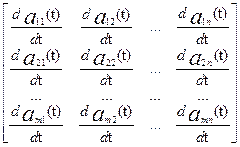 .
.
Производная от суммы двух матриц: 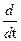 [A(t) + B(t)] =
[A(t) + B(t)] =  (t) +
(t) +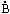 (t).
(t).
Производная от произведения двух
матриц: 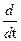 [A(t)B(t)] =
[A(t)B(t)] =  (t)B(t) + A(t)
(t)B(t) + A(t)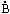 (t).
(t).
Подобно определению производной
от матрицы, интеграл от матрицы определяется как матрица, образованная из
интеграла от элементов исходной матрицы.
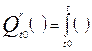 dt.
dt.
2. Определители.
Определителем, или детерминантом второго порядка матрицы А записывается как 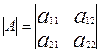 и его значение считается
равным (а11а22 – а12а21). Его порядок равен числу строк
квадратной матрицы или столбцов.
и его значение считается
равным (а11а22 – а12а21). Его порядок равен числу строк
квадратной матрицы или столбцов.
Определителем, или детерминантом третьего порядка, соответствующим матрице
А, называют число, полученное по
правилу
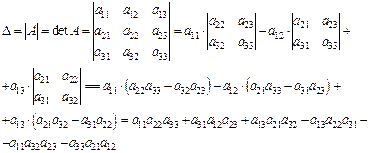
Схематически правило вычисления
определителя можно изобразить следующим образом:

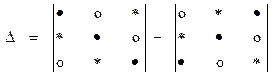 .
.
Свойства определителя:
- Определитель
равен единице, если все элементы на главной диагонали (а11, а22, а33,…,
аnn) равны единице, а остальные
нулю.
- Определитель
равен нулю, если равны нулю все элементы какой-либо строки или если равны
или пропорциональны соответствующие элементы произведения двух строк.
- Величина
определителя остается постоянной по модулю при перестановке его строк.
- Знак
определителя изменяется при перестановке двух его строк.
- Если
элементы некоторого ряда имеют общий множитель, то этот множитель можно
вынести за знак определителя.
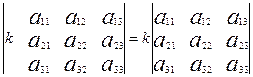 .
.
- Определитель
не изменяется, если к элементам некоторого ряда прибавить соответствующие
элементы параллельного ряда, умноженные на одно и тоже число.
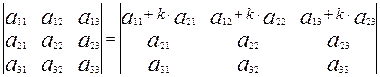 .
.
2.1. Миноры
и алгебраические дополнения.
Минором порядка S данной матрицы А (М) называется определитель, составленный
из элементов, стоящих на пересечении выбранных S строк и S столбцов.
Если
матрица А квадратная матрица, то вводится определение дополнительного минора.
Дополнительным минором ( ) называется определитель матрица, оставшийся после
вычеркивания S строк и S столбцов.
) называется определитель матрица, оставшийся после
вычеркивания S строк и S столбцов.
Пр.: 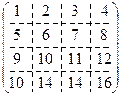
М =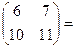 -4;
-4;  =
=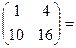 -24
-24
Алгебраическое дополнение минора – это
дополнительный минор, умноженный на (-1)р.
А = (-1)рּ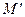 ,
,
где Р – сумма номеров строк и
столбцов данной матрицы, входящих в минор М.
Р = 2 + 3 + 2 + 3 = 10,
А = (-1)10ּ(-24) = -24.
Каждый
элемент aij матрицы, является
минором первого порядка, а дополнительным минором является определитель (n-1)-го
порядка, который называется минором aij и обозначается Мij.
2.2. Союзная
и обратная матрицы.
Союзной или
присоединенной матрицей называют квадратную матрицу, составленную из
алгебраических дополнений элементов и транспонирования.
А*= 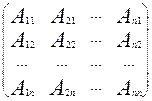 .
.
Матрица А-1
называется обратной матрицей к матрице А,
необходимо и достаточно, чтобы матрица была невырожденной и выполнялось условие
АА-1 = А-1А = I.
Невырожденной или несобственной матрицей называется матрица, определитель которой
отличен от нуля.
Производная от обратной матрицы.
Для
значения t,
при котором А(t)
дифференцируема и существует обратная матрица:
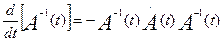 .
.
Специальные обратные матрицы:
а) АА-1 = 1 (матрица совпадает со
своей обратной матрицей).
б) А – ортогональная матрица, если А-1
= Ат.
в) А – унитарная, если А = {(А*)т}-1
(матрица, обратная матрице А, равная матрице, сопряженной с матрицей А).
3. Вектор.
Линейное пространство.
Скалярные
произведение:
Для
действительных х и у запишем как: <х, у>
= хт у = ут х = <у, x>.
Векторное произведение:
x><у = х(у*)т
= 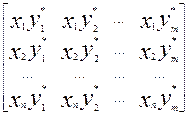 ,
,
если вектор-столбец х
(n×1) обозначить
через х>; вектор-строку (у*)т
(1×m) – через <y.
Ортогональные вектора:
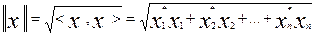
Единичные векторы.
Вектор
называется единичным, если его длина
равна единице так, что <
 > = 1.
> = 1.
Линейная зависимость.
Вектор хi
(i = 1, 2,…,m) с составляющими х1i, х2i,…, хni называются линейно независимыми, если не существует таких постоянных k1,
k2,…,
km, что
k1х1 + k2х2 +…+ kmхm = 0.
Квадратная
матрица называется особенной, если ее
столбцы или строки не являются линейно-независимыми (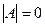 , а если
, а если 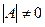 , то матрица неособенная). Если строки особенной матрицы
линейно связаны одним соотношением, то матрица – просто вырожденная. Если
более, чем одним соотношением, то – многократно вырожденной.
, то матрица неособенная). Если строки особенной матрицы
линейно связаны одним соотношением, то матрица – просто вырожденная. Если
более, чем одним соотношением, то – многократно вырожденной.
Рангом (r)
матрицы (А) является наивысший порядок миноров матрицы А, отличных от нуля: r = n – g (n – порядок).
Определитель Грамма:
Система
однородных уравнений имеет нетривиальное решение для ki только в
том случае, если определитель матрицы с коэффициентами [<xi; xj>] равен нулю. Этот определитель
называется определителем Грама и
равен:
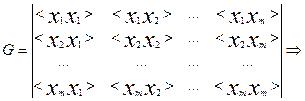 система векторов линейно независимая тогда и только тогда,
когда определитель Грама ≠ 0.
система векторов линейно независимая тогда и только тогда,
когда определитель Грама ≠ 0.
3.1. Линейное пространство.
Наиболее простым примером линейного векторного пространства служит множество
векторов, принадлежащих трехмерному пространству (эвклидову). Если система векторов х1, х2,…,
хm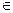 S, то и множество векторов (у), являющихся линейной комбинацией этих
векторов, т.е. у = k1х1 + k2х2 +…+ kmхm,
образующееся векторное пространство.
S, то и множество векторов (у), являющихся линейной комбинацией этих
векторов, т.е. у = k1х1 + k2х2 +…+ kmхm,
образующееся векторное пространство.
Базисом пространства называется такая
система векторов, что произвольный вектор пространства выражается единственным
образом в виде линейной комбинации этих векторов.
Если
задана система, состоящая из m линейно независимых векторов, то при помощи
исходной системы векторов можно построить ортогональную систему из m линейно
независимых векторов. Если длина каждого вектора в ортогональной системе равна
единице, то такая система называется ортонормированной.
3.2. Правило
Крамера для решения линейных уравнений.
Правило Крамера.
Задана
исходная система:
а11х1 + а12х2
+…+ а1nхn = у1
а21х1 + а22х2
+…+ а2nхn = у2
……………………………….
аn1х1 + аn2х2
+…+ аnnхn = уn
В более компактной форме: 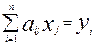 (i = 1, 2,…, n), или Ах = у, где
(i = 1, 2,…, n), или Ах = у, где
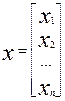 ,
, 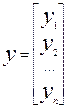 .
.
Итак,
правило Крамера для построения решения при помощи определителей можно
сформулировать следующим образом: система (n) линейных алгебраических уравнений с (n) неизвестными х1, х2,…,
хn имеет решение, если матрица А несобственная.
Значение
искомой переменной равно постоянному значению от деления двух определителей.
Знаменатель равен определителю матрицы коэффициентов системы, а числитель равен
определителю матрицы коэффициентов, k-й столбец в которой заменим столбцом,
содержащие члены из правой части системы уравнений.
3.3. Однородная
система уравнений.
Если члены в правой части
уравнения равны нулю, то система уравнений называется однородной.
Предположим,
что ранг матрицы коэффициентов равен r.
1)
Опускаем q = n – r уравнений так, чтобы определитель матрицы
коэффициентов относительно r неизвестных
отличался от нуля.
2)
Образуем r уравнений с r неизвестными в левой части
уравнения и оставшимся
q = n – r неизвестными в правой части. r неизвестных выражается через q = n – r неизвестных (q деферент А).
Получаем q независимых решений в
результате указанных этапов решения.
4. Собственные
числа.
От характеристических
значений системы зависит ее динамические свойства.
у = Ах, где у и х – векторы столбцы, а А – квадратная матрица (n×n).
у = Ах = λх, где λ –
скалярный коэффициент пропорциональности.
Значение λ (λi), для
которого уравнение у = Ах имеет решение xi ≠ 0 называется собственным или характеристическим числом А. Соответственный вектор
решения xi ≠ 0 называется собственным или характеристическим вектором
А.
4.1. Характеристическое
уравнение.
Многочлен n-й
степени относительно А, определенный уравнением 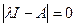 , называется характеристическим
уравнением А.
, называется характеристическим
уравнением А.
Р(λ) = λn + a1
λn-1 + a2
λn-2 +…+ an-1
λ + an = 0. Корни характеристического уравнения равны
собственным или характеристическим значениям А.
5. Билинейная
и квадратичная форма.
Билинейной формой относительно переломных хi, уi, называется выражение
вида:
В = a11x1y1 + a12x1y2 +…+ a1nx1yn + a21x2y1 + a22x2y2 +…+a2nx2yn+…+ an1xny1
+…+annxnyn, где все составляющие – действительные величины.
Комплексная форма: 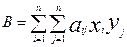 , или в матричной форме:
, или в матричной форме:
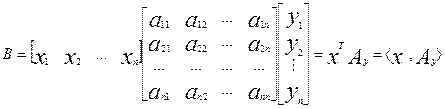
Матрица А – матрица
коэффициентов формы, ранг А – ранг формы. Если х = у, то предыдущее уравнение превратится в: Q = xTAx = <x, Ax>.
Q называется квадратичной
формой x1, x2,…,
xn.
Или: 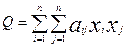 .
.
Преобразование переменных.
Линейное преобразование х
= Ву, где В – произвольная неособенная матрица (n×n), преобразует Q в квадратичную форму относительно у1,
у2,…,
уn: Q = yTBTABy или Q = утСу,
где С = ВтАВ.
6. Матричные
многочлены.
Степени матрицы.
AkAm = Ak+m
(Ak)m = Akm
A0 = In
(A-1)m =
A-m
Если Am = В, где А –
квадратная матрица, то A – корень m-той степени В.
Матричные многочлены.
N(x) = Pnxn + Pn-1xn-1 +…+ P1x + P0 (х – скалярная переменная).
х заменяем
квадратной матрицей А, то:
N(A) = PnAn
+ Pn-1An-1 +…+ P1A + P0In.
Бесконечные ряды матриц.
Запишем:
S(A) = a0In + a1A
+ a2A2 +…+ anAn +…= 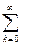 akAk, тогда геометрический ряд:
akAk, тогда геометрический ряд:
G(A) = I + aA +
a2A2 +…= 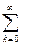 akAk.
akAk.
Экспоненциальная функция:
eA = expA = I +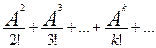
Синусоидальная функция:
sinA = A - 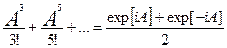 .
.
Косинусоидальная функция:
cosA = I -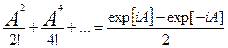 .
.
Гиперболический синус:
shA = A + .
.
Гиперболический косинус:
chA = I +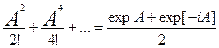 .
.
Теорема Кэли-Гамеильтона.
I0
= 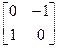 - действительная матрица (2×2) (аналог j =
- действительная матрица (2×2) (аналог j = 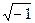 ).
).
sin aI0 = aI0
+ 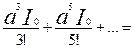 I0 sha. Обобщим: Ар = МАрМ-1.
I0 sha. Обобщим: Ар = МАрМ-1.
Если N(λ) – многочлен от λ вида: N(λ) = λn + C1 λn-1 +…+ Cn-1 λ + Cn, то
N(A) = An + C1An-1
+…+ Cn-1A + CnI = MN(λ)M-1 = M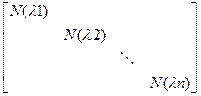 M-1, где λ1, λ2,…,
λn – не нули N(λ).
M-1, где λ1, λ2,…,
λn – не нули N(λ).
Если N(λ) = Р(λ1),
то N(λ1) = N(λ2) =…= N(λn) = 0  Р(А) = [0], где
Р(А) = [0], где
Р(λ) = |λI –A|  матрица А удовлетворяет своему характеристическому уравнению.
матрица А удовлетворяет своему характеристическому уравнению.
Теорема Сельвестра.
Если N(A) –
матричный многочлен от А и если квадратная матрица А содержит n различных характеристических
чисел, то многочлен от А можно записать в виде:
 , где
, где 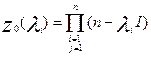
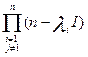 .
.
Согласно теореме
Кэли-Гамильтона:
N(A)=a1An-1 + a2An-2 +…+ an-1A + anI (произвольный матричный многочлен N(A))
запишется многочленом А с наивысшей степенью n–1.
Теорема Сельвестра. Вырожденная
форма.
Если модифицировать
уравнение: N(A) = 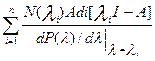 (в том случае, когда А
содержит кратные характеристические числа), тогда она (модификация) будет называться
вырожденной формой теоремы Сильвера.
(в том случае, когда А
содержит кратные характеристические числа), тогда она (модификация) будет называться
вырожденной формой теоремы Сильвера.
Если характеристический
корень имеет порядок S, то можно
показать, что N(A), обусловленная I корнем λi, равно:
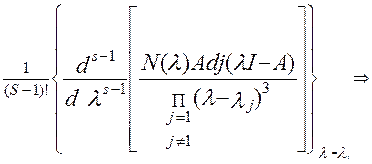
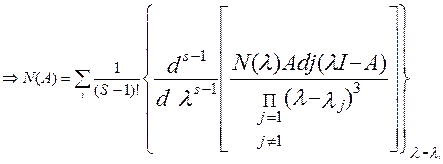
Метод Кэли-Гамильтона.
Рассмотрим случай, когда степень матричного многочлена N(A) выше,
чем порядок А.
Делим N(λ) на характеристический многочлен А:
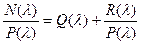 , R(λ) – остаточный член. Затем умножаем Р(λ):
, R(λ) – остаточный член. Затем умножаем Р(λ):
N(λ) = Р(λ)Q(λ) + R(λ). Если
Р(λ) = 0, то N(λ) = R(λ).
Т.к. P[A] = [0], то матричная функция N(A) = R(A).
А если Q(λ) – аналитическая функция в области, то F(λ) = Q(λ)Р(λ) + R(λ)
(*), где Р(λ) – характеристический многочлен А, а R(λ) –
многочлен вида:
Р(λ) = а0 + а1λ +
а2 λ2 +…+ аn-1 λn-1.
 Т.к.
Р(λi)=0, то F(λ1) = R(λ1)
Т.к.
Р(λi)=0, то F(λ1) = R(λ1)
F(λ2) = R(λ2)
…………….
F(λ2) = R(λn)
Покажем, что 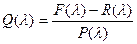 - аналитическая
функция λ. Нули знаменателя служат нулями и числителя, то Q(λ) – аналитическая функция. Поэтому
уравнение (*) справедливо для всех λ. Вместо λ можно подставить А: F(А) = Q(А)Р(А)
+ R(А). По теореме Кэли-Гамильтона:
Р(А) = 0
- аналитическая
функция λ. Нули знаменателя служат нулями и числителя, то Q(λ) – аналитическая функция. Поэтому
уравнение (*) справедливо для всех λ. Вместо λ можно подставить А: F(А) = Q(А)Р(А)
+ R(А). По теореме Кэли-Гамильтона:
Р(А) = 0 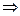 F(А) = R(А).
F(А) = R(А).
7. Функциональное
пространство.
Здесь рассмотрим такую
систему из n функций
f1(t),…, fn(t), определенных на интервале (а,
b), что ни одна функция fi(t) не
является линейной комбинацией любых других (n-1) функций из этого интервала.
Скалярное произведение.
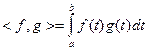 . Для комплексных функций действительного переменного t:
. Для комплексных функций действительного переменного t: 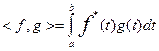 .
.
Норма функция.
Норма f = || f ||1/2 = <f, f>1/2
= [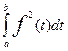 ]1/2. Нормированной функцией называется
функция, норма которой равна единице.
]1/2. Нормированной функцией называется
функция, норма которой равна единице.
Ортогональные функции.
Две функции f(t) и g(t),
ортогональны на (а, b), если <f, g> =
0. Система нормированных функций φ1(t), φ2(t) называется ортонормированной,
если < φi, φj> = δij.
Ортогональные функции в качестве базиса функционального пространства.
Рассмотрим бесконечную ортогональную систему функций φ1(t), φ2(t),… в
качестве координатных векторов, то по аналогии f(t) вектор
этого пространства, а разложение:
Сk =
<f, φk>.
Если F(t)
апроксимируется линейной комбинацией n нормированных
функций
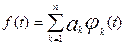 (a < t < b), то получится аппроксимация: ak = ck. Затем
(a < t < b), то получится аппроксимация: ak = ck. Затем 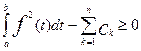 (*) – неравенство Бесселя.
(*) – неравенство Бесселя.
Заданная ортонормированная
система φ1(t), φ2(t),…, φn(t)
называется полной, если производная
кусочно-непрерывная f(t) может апроксимироваться в среднем этой системы
со сколь угодно малой ошибкой при большом количестве ее членов, т.е.
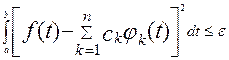 или
или 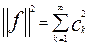
Ортогональная система с «весом».
Вводим весовую функцию ω(t): 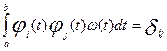 . Эта функция выбирается для выделения области на (a, b).
Говорят, что φk(t)
ортонормированны относительно данной «весовой» функции. Коэффициенты Фурье f(t)
определяются как:
. Эта функция выбирается для выделения области на (a, b).
Говорят, что φk(t)
ортонормированны относительно данной «весовой» функции. Коэффициенты Фурье f(t)
определяются как:

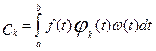 .
.
8. Метрическое пространство.
Пусть X
– произвольное множество. Понятие расстояния между элементами из X получается путем обобщения
фундаментальных свойств, которые можно интуитивно ожидать от понятия
расстояния.
Свяжем с каждой парой элементов из X некоторое вещественное неотрицательное
число 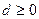 . Это число называется расстоянием
или метрикой в X, если для любых
. Это число называется расстоянием
или метрикой в X, если для любых  оно удовлетворяет
следующим трем условиям:
оно удовлетворяет
следующим трем условиям:
- d(x, y)=0 тогда и только тогда, когда
х=у (аксиома идентичности);
- d(x, y)=d(y, x) (аксиома симметрии);
- для
любой тройки
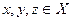 имеет место d(x,
у) ≤ d(x, z)+d(z, у) (аксиома треугольника).
имеет место d(x,
у) ≤ d(x, z)+d(z, у) (аксиома треугольника).
Метрическим пространством называется пара (X, d), т. е. множество X с определенной на нем метрикой d. Элементы множества X называют точками
метрического пространства (X,
d).
Из данного определения следует, что множество X только тогда превращается в
метрическое пространство, когда в него введена соответствующая метрика d(x, у). Если в одном и том же множестве X ввести различные метрики,
то получатся и различные пространства.
Заключение.
В данном реферате я
рассмотрел основные понятия линейной алгебры и матричного множества, что
необходимо для успешного освоения курса математических основ теории систем.
Используемая
литература.
- Беклемишев
Д.В. Курс аналитической геометрии и линейной алгебры. М., 1975.
- Чемоданов
Б.К. «Математические основы теории автоматического регулирования», Москва
1977 г.
- Коршунов
Ю.М. «Математические основы кибернетики», Москва 1987 г.
- Пискунов
Н.С. Дифференциальное и интегральное исчисления. М., 1978, Т. 1, Т. 2.