ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ И НАУКЕ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ГОУ ВПО

ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

СЕРПУХОВСКОЕ ПРЕДСТАВИТЕЛЬСТВО



       ФАКУЛЬТЕТ: финансово-кредитный

      КАФЕДРА: высшей математики




КОНТРОЛЬНАЯ РАБОТА №2

ПО ДИСЦИПЛИНЕ: «Теория вероятностей и математическая статистика»

 

                                                                    Исполнитель:                   Жмыхова Юлия Николаевна

                                      Специальность:              финансы и кредит

                                                                    Курс:                                  2

                                                                    Группа:                              255

                             № зачётной книжки:      05УБД71019

                                               Руководитель:                Борисова Вера Ионовна

Г. Серпухов

2007

Задание №1. Чтобы установить содержание золы в каменном угле из очень большой партии было взято 500 проб. Результаты анализа приведены в таблице:

Содержание золы,%

5-7

7-9

9-11

11-13

13-15

15-17

17-19

19-21

Итого

Число проб

33

71

107

119

92

50

21

7

500

Найти:

а) вероятность того, что процент зольности всей партии отличается от среднего выборочного не более чем на 0,5% (по абсолютной величине);

б) границы, в которых с вероятностью 0,95 заключена доля проб угля этой партии, содержащего не более 13% золы;

в) объём бесповоротной выборки, при котором те же границы для указанной доли (см. п. б) можно гарантировать с вероятностью 0,9876.


Решение:

а) среднеквадратичекое оклонение выборочного среднего находим по формуле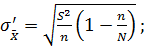  

Вероятность оклонения от среднего значения будет равна



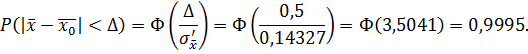
б) определяем выборочную долю банков по формуле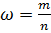

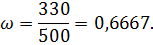
Среднеквадратичное отклолнение выборочной доли при больших N найдём по формуле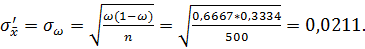

Вероятность отклонения выборочной доли от генеральной доли находим по формуле  .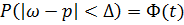

Квантиль уровня надёжности 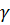 находим из условия

Ф(t)=0,95;

Построим доверительный интервал:

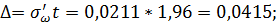
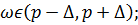
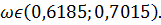
в) находим t: Ф(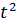)=0,9876,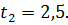

Определим 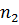 из пропорции

;

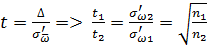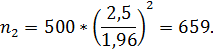
Ответ: а) 0б9995; б) (0,6185;0,7015); в) 659.

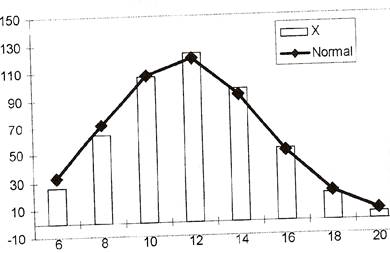
Задание №2. По данным задачи 1, используя х2-критерий Пирсона, при уровне значимости а=0,05 проверить гипотезу о том, что случайная величина Х – процент зольности угля – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соотетствующую нормальную кривую.

Решение:

i

Xi,

Xi+1

середина Xi

Ni

XiNi

NiXi^2

Pi

NPi

(Ni-NPi)^2

(Ni-NPi)^2/NPi

1

5

7

6

33

198

1188

0,051

25,68

53,51

2,08

2

7

9

8

71

568

4544

0,127

63,27

59,73

0,94

3

9

11

10

107

1070

10700

0,213

106,53

0,22

0

4

11

13

12

119

1428

17136

0,245

122,62

13,12

0,11

5

13

15

14

92

1288

18032

0,193

96,5

20,26

0,21

6

15

17

16

50

800

12800

0,104

51,92

3,68

0,07

7

17

19

18

21

378

6804

0,038

19,09

3,65

0,19

8

19

21

20

7

140

2800

0,01

4,79

4,86

1,01

Σ

 

 

 

500

5870

74004

 

 

 

4,6233

           

               Вычислиим необходимые суммы. Параметры нормального закона рапределения заменим наилучшими оценками по выборке

 .

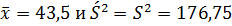Находим критическое значение 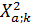 при числе степеней свободы k=m-r-1:

k=8-2-1=5;

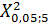=11,1;

наблюдаемое значение Х2=4,6233;

т.к. 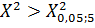, то гипотеза о нормальном распределени процента зольности угля принимается.


Ответ: гипотеза принимается.














Задание №3. Рапределение 100 семей по доходу на члена домохозяйства Х(тыс.руб.) и потребления мяса Y(кг) за месяц дано в таблице:

 

2

4

6

8

10

Итого

0,5

10

4

 

 

14

1

6

10

2

 

18

1,5

 

15

12

 

27

2

 

14

2

1

17

2,5

 

9

3

1

13

3

 

 

5

6

11

Итого

16

29

37

10

8

100

               Необходимо:

1)    Вычислить групповые средние  и  и 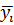построить эмпирические линии регрессии.

2)    Предпологая, что между переменными X иY существует линейная корреляционная зависимость:

а) найти уравнения прямых регрессий, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпритацию полученных уравнений;

б) вычислить коэффициент корреляции, на уровне а=0,05 оценить его значимость, сделать вывод о тесноте и направлении связи между переменными X и Y;

в) используя соответствующее уравнение регрессии, оценить среднемесячное потребление мяса, если доход на члена семьи составляет тысячу рублей.







Решение:

Xi/Yj

2

4

6

8

10

Итого

Yi

NiXi

NiXi2

Xcp

1,65

0,5

10

4

 

 

 

14

2,571

7

3,5

Ycp

5,3

1

6

10

2

 

 

18

3,556

18

18

S2X

0,583

1,5

 

15

12

 

 

27

4,889

40,5

60,75

S2Y

4,91

2

 

 

14

2

1

17

6,471

34

68

µ

1,455

2,5

 

 

9

3

1

13

6,769

32,5

81,25

bxy

0,657

3

 

 

 

5

6

11

9,091

33

99

byx

1, 906

Итого

16

29

37

10

8

100

 

165

330,5

r=

0,86

Xj

0,688

1,19

1,905

2,65

2,813

 

 

1,65

0,583

t=

20,282

NjYj

32

116

222

80

50

530

5,3

 

 

 

 

NjYj2

64

464

1332

640

800

3300

4,91

 

 

 

 

ΣNijXiYj

22

138

423

212

225

1020

1,455

 

 

 

 

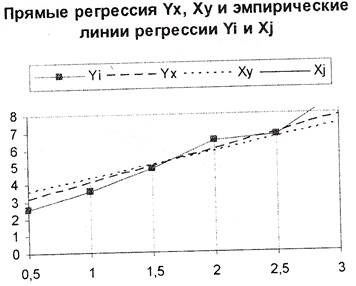
               Сделаем необходимые вычисления. Найдём групповые средние значения и дисперсию переменных X и Y, их ковариацию. Итоговые результаты сгруппируем в крайнем правом столбце. Построим эмпирическими линиями регрессии .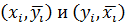

Найдём средние значения дохода на члена домохозяйства M(X)=1,6500 (тыс.руб.) и потребления мяса M(Y)=5,3000(кг), выборочные дисперсии  S2(X)=0,5825; S2(Y)=4,9100 и ковариацию K=M(XY)-M(X)M(Y)=1,4550.

Найдём коэффициенты регрессии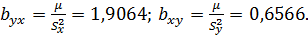

Коэффициент 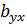 показывает, что при увеличении дохода на члена домохозяйства на 1 тыс.руб. потребление мяса увеличивается в среднем на 1,9 кг за месяц.

Коэффициент 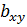 показывает, что для увеличения потребления мяса на 1 кг за месяц надо увеличить доход на члена домохощяйства в среднем на 0,66 тыс. руб.


Составим уравнение прямых регрессии Yx и Xy и построим эти линии

Yx – 5,3=1,9064(х-1,65);

Xy – 1,65=0,6566(y-5,3).

               б) Выборочный коэффициент корреляции равен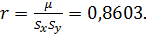

Связь между перемнными X и Y тесная прямая, т.к.

Оценим значимость r:

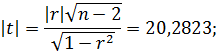
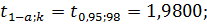
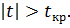
Между переменными X и Y существует линейная корреляционная связь.

               в) При доходе на члена семьи X в тысячу руьлей потребление мяса  Y в месяц будет равно в среднем

yx - 5,3=1,9064(x-1,65);

yx = 5,3+1,9064(1-1,65);

yx = 4,0608 (кг).


Ответ:  yx - 5,3=1,9064(x-1,65); Xy – 1,65=0,6566(y-5,3); ;

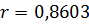       при Х=1 тыс.руб. Y=4,0608 кг.


 

 

 

 

 

 

 

 

 

 

Список литературы.


Кремер Н.Ш. «Теория вероятностей и математическая статистика»

«ЮНИТИ-ДАНА», Москва, 2002