Содержание
Введение. 3
1. Понятие ценных
бумаг и их виды.. 4
2. Портфель ценных
бумаг. 6
3. Методики
формирования оптимальной структуры портфеля. 6
Заключение. 17
Список литературы.. 18
Введение
Ценные
бумаги - необходимый атрибут развития рыночного оборота. Эффективное управление
движением капитала в рамках фирмы предполагает вложение временно свободных
средств в ценные бумаги для извлечения дополнительной прибыли от роста курсовой
стоимости ценной бумаги. Безусловно, в настоящее время, вложения денежных
средств в российские ценные бумаги являются достаточно рискованным способом
приращения капитала, в связи с неразвитостью фондового рынка России, который
характеризуется:
Многие
коммерческие организации в настоящее время имеют достаточно большой объем
свободных средств, которые возможно как инвестировать в различные виды
деятельности, так и направить на приобретение ценных бумаг. При осуществлении
инвестирования в ценные бумаги организация, как и любой другой инвестор,
сталкивается с различными целями инвестирования.
Именно
портфель ценных бумаг является тем инструментом, с помощью которого может быть
достигнуто требуемое соотношение всех инвестиционных целей, которое недостижимо
с позиции отдельно взятой ценной бумаги, и возможно только при их комбинации. Функционирование
всей системы портфелей подчинено интересам обеспечения устойчивости и
рентабельности института, обеспечения устойчивости всей финансовой системы.
Этими
факторами обусловлен выбор темы курсовой работы – формирование портфеля ценных
бумаг.
Цель
работы – рассмотрение вопроса связанного с формированием портфеля ценных бумаг
1.
Понятие ценных бумаг и их виды
Объектами современного гражданского и хозяйственного оборота являются,
помимо материальных, движимых вещей, так
же и имущественные права, выраженные в определенной объективной форме - форме
документов. Эти документы в большинстве стран именуются ценными бумагами.
В большинстве стран под
ценными бумагами понимают документ, определяющий взаимоотношения между лицом,
выпустившим такой документ, и его владельцем и закрепляющий за владельцем
определенный набор имущественных прав, реализация которых возможна лишь при
предъявлении самого документа.
Из развития товарно-денежных
отношений видно, что ценная бумага - неизбежный результат развития торговых
отношений, не стесненных рамками излишней государственной и иной регламентацией.
Ценные бумаги воплощают права на определенные ресурсы, которые окружают
людей и могут являться объектом собственности, саму деятельность людей,
проявляющуюся в различного рода отношениях, урегулированных нормами права и
становящимися правоотношениями.
Существуют определенные
критерии разграничения, которые можно обозначить как признаки ценных бумаг:
обращаемость, гражданско-правовая обороноспособность, стандартность, документальность,
признание государством, рисковость, серийность, ликвидность.
Исходя
из рассуждений очевидно, что ценную бумагу делает ценной тот объем прав,
которые она удостоверяет. Отсюда следует, что ценными бумагами в юридическом
смысле являются различного рода ценные документы, которые представляют собой
ценность не сами по себе как объект материального мира в силу своих естественных
свойств, а именно в силу воплощенных в них права на определенные ценности -
товары, услуги, права, деньги и т. д.
На
сегодняшний день в мировой практике существует более 20 видов ценных бумаг. В
российской практике их несколько меньше - более 10.
В соответствии со ст. 143 ГК РФ: “К ценным
бумагам относятся: государственная облигация, облигация, вексель, чек,
депозитный и сберегательный сертификаты, банковская сберегательная книжка на
предъявителя, коносамент, акция, приватизационные ценные бумаги и другие
документы, которые законами о ценных бумагах или в установленных ими порядке отнесены
к числу ценных бумаг.”
Наиболее
распространенные виды:
-
акции. Это ценные бумаги, выпускаемые акционерными обществами без
установленного срока обращения. Акция удостоверяет внесение ее владельцем доли
в акционерный капитал (уставный фонд) общества. Акция дает следующие права: на
получение части прибыли в виде дивидендов; на продажу на рынке ценных бумаг; на
участие в управлении акционерным обществом; имущественное право. Привилегированные
акции дают право на получение заранее установленных дивидендов, но лишают права
участвовать в управлении. Простые (обыкновенные) акции позволяют получать
дивиденды, определяемые по итогам хозяйственной деятельности года, и дают право
голоса на собрании акционеров.
-
облигации. Облигация подтверждает, что ее владелец внес денежные средства на
приобретение ценной бумаги и тем самым вправе предъявить ее затем к оплате как
долговое обязательство, которое организация, выпустившая облигацию, обязана
возместить по номинальной стоимости, указанной на облигации. Такое возмещение
называют погашением облигации. Кроме выкупа в течение заранее обусловленного
при выпуске облигации срока, эмитент облигации обязан выплачивать их обладателю
фиксированный процент от номинальной стоимости облигации либо доход в виде
выигрышей или оплаты купонов к облигации. Облигации вправе выпускать
государство, местные органы (муниципалитеты), предприятия, компании, корпорации
на самые разные сроки (от года до двадцати пяти лет). Облигации выпускаются с
целью привлечения денежных средств, то есть представляют форму кредитования их
эмитентов лицами, купившими облигации. Облигации могут продаваться и покупаться
по свободному курсу на биржах.[1]
2.
Портфель ценных бумаг
Вложения юридических и физических
лиц в ценные бумаги требуют эффективного управления. В этой связи существует
понятие управления портфелем ценных бумаг.
В сложившейся мировой практике
фондового рынка под инвестиционным портфелем понимается некая совокупность
ценных бумаг, принадлежащих физическому или юридическому лицу, выступающая как
целостный объект управления. Смысл портфеля – улучшить условия инвестирования,
придав совокупности ценных бумаг такие инвестиционные характеристики, которые недостижимы
с позиции отдельно взятой ценной бумаги и возможны только при их комбинации.
Содержание управления портфелем
ценных бумаг – это планирование, анализ и регулирование состава портфеля,
осуществление деятельности по его формированию и поддержанию в целях достижения
поставленных задач обеспечения его доходности, эффективности при сохранении необходимого
уровня ликвидности и минимизации расходов на обслуживание. Портфель ценных бумаг
является инструментом, с помощью которого инвестору обеспечивается требуемая
устойчивость дохода при минимальном риске.
Наиболее важными параметрами
планирования и контроля в рамках управления портфелем ценных бумаг являются:
доходность портфеля, риск портфеля, определение стратегии в управлении портфелем.[2]
3. Методики формирования оптимальной структуры портфеля
На практике
используют множество методик формирования оптимальной структуры портфеля ценных
бумаг. Большинство из них основано на методике Марковица. Он впервые предложил
математическую формализацию задачи нахождения оптимальной структуры портфеля
ценных бумаг в 1951 году, за что позднее был удостоен Нобелевской по экономике.
Основными
постулатами, на которых построена классическая портфельная теория, являются
следующие:
1.
Рынок состоит из конечного числа активов, доходности
которых для заданного периода считаются случайными величинами.
2.
Инвестор в состоянии, например, исходя из
статистических данных, получить оценку ожидаемых (средних) значений доходностей
и их попарных ковариаций и степеней возможности диверсификации риска.
3.
Инвестор может формировать любые допустимые (для данной
модели) портфели. Доходности портфелей являются также случайными величинами.
4.
Сравнение выбираемых портфелей основывается только на
двух критериях – средней доходности и риске.
5.
Инвестор не склонен к риску в том смысле, что из двух
портфелей с одинаковой доходностью он обязательно предпочтет портфель с меньшим
риском.
Рассмотрим
подробнее сформировавшиеся на данный момент портфельные теории, некоторые из
которых будут применены далее при проведении практического расчета оптимального
портфеля ценных бумаг.
Модель Марковица
Основная идея
модели Марковица заключается в том, чтобы статистически рассматривать будущий
доход, приносимый финансовым инструментом, как случайную переменную, то есть
доходы по отдельным инвестиционным объектам случайно изменяются в некоторых
пределах. Тогда, если неким образом случайно определить по каждому
инвестиционному объекту вполне определенные вероятности наступления, можно
получить распределение вероятностей получения дохода по каждой альтернативе
вложения средств. Это получило название вероятностной модели рынка. Для
упрощения модель Марковица полагает, что доходы распределены нормально.
По модели Марковица определяются показатели,
характеризующие объем инвестиций и риск что позволяет сравнивать между собой
различные альтернативы вложения капитала с точки зрения поставленных целей и
тем самым создать масштаб для оценки различных комбинаций.
В модели
Марковица допустимыми являются только стандартные портфели (без коротких позиций).
Использую более техническую терминологию, можно сказать, что инвестор по
каждому активу находится в длинной позиции. Длинная позиция – это обычно
покупка актива с намерением его последующей продажи (закрытие позиции). Такая
покупка обычно осуществляется при ожидании повышения цены актива в надежде
получить доход от разности цен покупки и продажи.
Из-за
недопустимости коротких позиций в модели Марковица на доли ценных бумаг в
портфели накладывается условие неотрицательности. Поэтому особенностью этой
модели является ограниченность доходности допустимых портфелей, т.к. доходность
любого стандартного портфеля не превышает наибольшей доходности активов, из
которых он построен.
Для выбора наиболее приемлемого для инвестора портфеля
ценных бумаг можно использовать кривые безразличия. В данном случае эти кривые
отражают предпочтение инвестора в графической форме. Предположения, сделанные
относительно предпочтений, гарантируют, что инвесторы могут указать на
предпочтение, отдаваемое одной из альтернатив или на отсутствие различий между
ними.
Если же
рассматривать отношение инвестора к риску и доходности в графической форме,
откладывая по горизонтальной оси риск, мерой которого является
среднеквадратическое отклонение (sp), а по
вертикальной оси – вознаграждение, мерой которого является ожидаемая доходность
(rp), то можно получить семейство кривых
безразличия.
Располагая
информацией об ожидаемой доходности и стандартных отклонениях возможных
портфелей ценных бумаг, можно построить карту кривых безразличия, отражающих
предпочтения инвесторов. Карта кривых безразличия – это способ описания
предпочтений инвестора к возможному риску полностью или частично потерять
вкладываемые в портфель ценных бумаг деньги или получить максимальны доход.
Различные позиции инвесторов по отношению к риску можно
представить в виде карт кривых, отражающих полезность вложений в те или иные
инвестиционные портфели. Каждая из указанных на рисунке 3 позиций инвестора к
риску характерна тем, что любое уменьшение им риска сказывается на сокращении
доходности и стандартном отклонении каждого из портфелей. И поскольку портфеля
включает в себя набор различных бумаг, то вполне объяснимым является
зависимость его от ожидаемой доходности и стандартного отклонения его от
ожидаемой доходности и стандартного отклонения каждой ценной бумаги, входящей в
портфель.
Поэтому, с
точки зрения методологии модель Марковица можно определить как
практически-нормативную, что не означает навязывания инвестору определенного
стиля поведения на рынке ценных бумаг. Задача модели заключается в том, чтобы
показать, как поставленные цели достижимы на практике.[3]
Модель
Блека
Модель Блека
аналогична модели Марковица, но в отличии от последней в ней отсутствует
условие неотрицательности на доли активов портфеля. Это означает, что инвестор
может совершать короткие продажи, т.е. продавать активы, предоставленные ему в
виде займа. В этом случае инвестор рассчитывает на снижение курса ценной бумаги
и планирует вернуть заем теми же ценными бумагами, но приобретенными по более
низкому курсу.
В следствии
отсутствия ограничений на доли активов в портфеле потенциальная прибыль
инвестора не ограничена максимальной доходностью одного из активов, входящих в
портфель.[4]
Индексная
модель Шарпа
Как следует из
модели Марковица, задавать распределение доходов отдельных ценных бумаг не
требуется. Достаточно определить только величины, характеризующие это
распределение: математическое ожидание, среднеквадратическое отклонение и
ковариацию между доходностями отдельных ценных бумаг. На практике для сравнительно
небольшого числа ценных бумаг произвести такие расчеты по определению
ожидаемого дохода и дисперсии возможно. При определении же коэффициента
корреляции трудоемкость весьма велика.
В 1960-х годах
Уильям Шарп первым провел регрессионный анализ рынка акций США. Для избежания
высокой трудоемкости Шарп предложил индексную модель. Причем он не разработал
нового метода составления портфеля, а упростил проблему таким образом, что
приближенное решение может быть найдено со значительно меньшими усилиями.
В индексной
модели Шарпа используется тесная корреляция между изменением курсов отдельных
акций. Предполагается, что необходимые входные данные можно приблизительно
определить при помощи всего лишь одного базисного фактора и отношений,
связывающих его с изменением курсов отдельных акций. Как правило, за такой
фактор берется значение какого-либо индекса.
Модель
Тобина с безрисковым активом
В отличие от моделей Марковица и Блека, которые связаны с
выбором класса допустимых портфелей, модель Тобина в большей степени относится
к структуре рынка, нежели к структуре допустимых портфелей. В этой модели
предполагается существование безрискового актива, доходность которого не зависит
от состояния рынка и всегда имеет одно и то же значение. Поскольку неопределенность
конечной стоимости безрискового актива отсутствует, то стандартное отклонение
для этого актива равно нулю. Это означает, что корреляция между ставкой
доходности по безрисковому активу и ставкой доходности по любому рисковому
активу равна нулю.
Дж. Тобин
показал, что если Q = (pi, …, pn) –
некоторый портфель (pi – доля i-го актива в портфеле), а f – безрисковый актив, то все портфели
вида
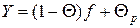
лежат на
прямой, проходящей через точки (0, rf) и (sp, rp), где rf и rp – безрисковая и рисковая доходности
соответственно. Среди всех таких прямых нужно выбрать самую крутую (более
крутая дает большую доходность при заданном риске), т.е. ту, которая проходит
через точку (0, rp) и точку касания T к эффективной границе.
В модели
оценки финансовых активов новую эффективную границу, полученную с учетом
безрискового актив, называют рыночной линией (Capital Market Line, CML), а портфель Т – рыночным портфелем.[5]
Алгоритм Элтона-Грубера-Падберга
При определении
структуры касательного портфеля Т в
модели с безрисковым активом можно также воспользоваться методом критических
линий, как и в модели Марковица. Но имеется и другой метод определения
структуры этого портфеля, который не требует определения «угловых» портфелей и,
следовательно, является более простым.
Предполагается,
что доходности ценной бумаги могут быть описаны рыночной моделью (индексной
моделью Шарпа), а также, что существует возможность безрискового заимствования
и кредитования по ставке rf. Метод разработан
Элтоном, Грубером и Падбергом.
Алгоритм
начинается с замечания, что наклон линии, выходящей из точки rf и проходящей через любой конкретный портфель
равен:
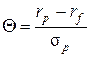 .
.
«Касательный»
портфель Т определяется как имеющий
максимальную тхэту (Q).
Для поиска портфеля, имеющего максимальную Q, применяется следующий
пятишаговый алгоритм:
1. Упорядочить ценные бумаги в порядке убывания отношений
доходности к систематическому риску (reward-to-volatility ratio):
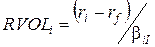 ,
,
где ri
– ожидаемая доходность i-й ценной
бумаги;
rf –
безрисковая ставка;
biI – коэффициент «бета».
Числитель этого выражения представляет собой ожидаемое
«вознаграждение» за приобретение ценной бумаги, а знаменателем является
соответствующий ей b-коэффициент.
Это отношение иногда называют отношением Трейнора.
2. Начиная с ценной бумаги, имеющей наибольшее RVOLi, добавлять ценные
бумаги одну за другой и вычислять Fi:
 ,
,
где s2I – систематический риск – дисперсия рыночного индекса;
s2eI
– несистематический риск – дисперсия случайной ошибки.
3. Сравнивать величины Fi с соответствующими RVOLi
до тех пор, пока Fi меньше RVOLi. С некоторого момента это соотношение изменится на
противоположное. Пусть k –
максимальный номер, для которого это соотношение еще не выполнено. Тогда ценные
бумаги с 1 по k будут иметь не
нулевые веса в портфеле Т, а
остальные – нулевые. Таким образом, Fk
является «ставкой отсечения» для RVOL.
4. Вычислить величины Zi,
чтобы определить, с какими весами будут входить в портфель первые k ценных бумаг:
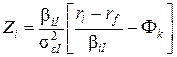 .
.
Значения Zi для i =
k + 1, ..., N
полагаются равными нулю.
5. Разделить каждую Zi на сумму Zi для получения весов
для ценной бумаги:
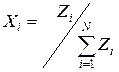
Это сделать необходимо, так как сумма Zi обычно не равна единиц.
Полученные
значения Xi и являются долями
ценных бумаг в портфеле Т.[6]
Модель
оценки финансовых активов
Некоторые из предположений, на которых основывается модель
оценки финансовых активов (Capital Asset Prising Model, CAPM), совпадают с
предположениями нормативного подхода к инвестированию, описанного в предыдущих
разделах. Эти предположения дополняются следующими:
1.
Для всех инвесторов период вложения одинаков.
2.
Безрисковая процентная ставка одинакова для всех
инвесторов.
3.
Информация свободно и незамедлительно доступна для всех
инвесторов.
4.
Инвесторы имеют однородные ожидания, т.е. они одинаково
оценивают ожидаемые доходности, среднеквадратичные отклонения и ковариации
доходностей ценных бумаг.
Как вытекает
из этих предположений, в модели оценки финансовых активов рассматривается
предельный случай. Все инвесторы обладают одной и той же информацией и
по-одинаковому оценивают перспективы ценных бумаг. Неявно это означает, что они
одинаковым образом анализируют получаемую информацию. Рынки ценных бумаг
являются совершенными рынками в том смысле, что в них нет факторов, которые бы
препятствовали инвестициям. Это позволяет сместить фокус рассмотрения с того,
как следует инвестору размещать свои средства, на то, что произойдет с курсами
ценных бумаг, если все инвесторы будут поступать одинаково. Исследуя
коллективное поведение всех инвесторов на рынке, можно выявить характер
конечной равновесной зависимости между риском и доходностью каждой ценной
бумаги.
Сначала инвесторы анализируют ценные бумаги и определяют
структуру «касательного» портфеля. В итоге, в равновесном случае все инвесторы
выбирают один и тот же «касательный» портфель, т.к. оценки инвесторов относительно
ожидаемых доходностей бумаг, их дисперсий и ковариаций, а также величины безрисковой
процентной ставки полностью совпадают. К тому же линейное эффективное множество
является одним и тем же для всех инвесторов, так как оно состоит из комбинаций
согласованного «касательного» портфеля и безрискового заимствования или
кредитования.
В связи с тем
что все инвесторы имеют одно и то же эффективное множество, единственной
причиной, по которой они предпочтут различные портфели, является то, что они
характеризуются различными кривыми безразличия. Хотя выбранные портфели будут
различными, каждый инвестор выберет одну и ту же комбинацию рискованных бумаг,
обозначенных на рисунке 2.5 через Т.
Это означает, что каждый инвестор распределит свои средства среди рискованных
бумаг в одной и той же относительной пропорции, увеличивая безрисковое заимствование
или кредитование с целью достижения предпочтительной для него комбинации риска
и дохода. Это свойство модели оценки финансовых активов часто называют теоремой
разделения: «Оптимальная для инвестора комбинация активов не зависит от его
предпочтения относительно риска и дохода».
Другими
словами, оптимальная комбинация рискованных активов может быть определена без
построения кривых безразличия каждого инвестора.
Объяснением теоремы разделения служит то, что все
портфели, расположенные на линейном эффективном множестве, включают в себя
инвестирование в «касательный» портфель в сочетании с различным уровнем
безрискового заимствования или кредитования. В модели оценки финансовых активов
каждый инвестор сталкивается с одним и тем же линейным эффективным множеством.
Это означает, что все будут инвестировать в один и тот же «касательный»
портфель (в сочетании с определенным объемом безрискового заимствования и
кредитования, который определяется кривой безразличия каждого инвестора). Из
этого следует, что доля рискованных ценных бумаг в портфеле каждого инвестора будет
одной и той же.
Другим важным
свойством модели оценки финансовых активов является то, что в состоянии
равновесия каждый вид ценных бумаг имеет ненулевую долю в «касательном»
портфеле. Основанием этого свойства является теорема разделения, которая
утверждает, что доля рискованных активов в портфеле каждого инвестора не
зависит от предпочтения инвестора относительно риска и доходности. Эта теорема
основывается на том, что рискованная доля портфеля каждого инвестора
представляет собой просто инвестирование в Т.
Если каждый инвестор приобретает Т и
при этом Т не включает в себя
инвестиций в каждый вид бумаг, то получается, что никто не инвестировал в те
бумаги, которые имели нулевую долю в Т.
Это должно привести к тому, что курсы ценных бумаг с нулевой долей в Т упадут, вызвав рост их ожидаемой
доходности до тех пор, пока в «касательном» портфеле их доля станет отличной от
нуля.
В результате
соотношение долей каждой бумаги в «касательном» портфеле в состоянии равновесия
будет соответствовать соотношению долей бумаг в так называемом рыночном
портфеле. Рыночный портфель – это портфель, состоящий из всех ценных бумаг, в
котором доля каждой соответствует ее относительной рыночной стоимости.
Относительная рыночная стоимость ценной бумаги равна ее совокупной рыночной
стоимости, деленной на сумму совокупных рыночных стоимостей всех ценных бумаг.
Индексная
модель Шарпа была описана выше В ней предполагалось, что доход по обыкновенной
акции связан с доходом по рыночному индексу.
Естественно
задаться вопросом о взаимосвязи индексной модели рынка и модели оценки
финансовых активов. Прежде всего следует заметить, что в обеих моделях величина
наклона именуется как «бета» и обе каким-то образом связаны с рынком. Однако
между ними существует два значительных различия.
Первое
заключается в том, что индексная модель рынка является факторной моделью. И в
отличие от модели оценки финансовых активов она не является равновесной
моделью, описывающей процесс формирования курсов ценных бумаг.
Второе состоит
в том, что рыночная модель использует рыночный индекс, в то время как САРМ-модели – рыночный портфель. Рыночный
портфель сочетает в себе все обращающиеся на рынке бумаги, а рыночный индекс –
только ограниченное их число. Поэтому концептуально коэффициент biI из рыночной модели отличается от коэффициента biM из модели оценки финансовых активов. Это связано с
тем, что «бета» в рыночной модели измеряется относительно рыночного индекса, а
«бета» в САРМ-модели – относительно рыночного портфеля. На практике, однако, в
связи с тем, что точно определить структуру рыночного портфеля не удается,
используют рыночный индекс. Поэтому «бету», определенную с помощью рыночного
индекса, несмотря на концептуальное различие, принимают в качестве оценки
«беты» в модели оценки финансовых активов.[7]
Заключение
Под ценными
бумагами понимают документ, определяющий взаимоотношения между лицом,
выпустившим такой документ, и его владельцем и закрепляющий за владельцем
определенный набор имущественных прав, реализация которых возможна лишь при
предъявлении самого документа. Вложения в ценные бумаги требуют эффективного
управления. В этой связи существует понятие управления портфелем ценных бумаг,
который представляет собой некую совокупность ценных бумаг, выступающую как
целостный объект управления. Наиболее важными параметрами в управлении
портфелем ценных бумаг являются: доходность портфеля и его риск. Доходность
портфеля зависит от ожидаемых доходностей входящих в него различных активов.
Риск портфеля ценных бумаг зависит от сочетания стандартных отклонений
(дисперсий) активов и степени взаимосвязи и направления изменения доходностей
(ковариаций) активов, входящих в его состав.
В данной
работе представлена статическая модель оптимального портфеля ценных бумаг. Эта
модель может быть использована при инвестировании, управлении портфелем ценных
бумаг отдельным предпринимателем или инвестором для более успешной предпринимательской
деятельности. Недостатком данной модели является то, что она не учитывает
влияние всех факторов, влияющих на риск портфеля ценных бумаг. Также к
недостатку данной модели можно отнести и тот факт, что не для всех ценных бумаг
можно составить статистический ряд доходности актива за предыдущие периоды.
Существуют
различные модели оптимизации портфеля ценных бумаг (такие как модель Марковица,
индексная модель Шарпа, модель выравненной цены и др.). Все они, так или иначе,
имеют некоторые недостатки, но применение их на практике дает значительные
преимущества при управлении портфелем ценных бумаг.
Список
литературы
1.
Буренин А.Н. Рынок ценных бумаг и производных
финансовых инструментов: Учеб. пособие. – М.: Открытое общество, 2002. – 347 с.
2.
Галанов В.А., Басов А.И. Рынок ценных бумаг. - М.:, Финансы и статистика, 2002. – 388 с..
3.
Касимов Ю.Ф. Основы теории оптимального портфеля ценных
бумаг. – М.: Филинъ, 2002. – 144 с.
4.
Миркин Я.М. Ценные бумаги и фондовый рынок. –
М.: Перспектива, 2000. – 368 с.
5.
Рынок ценных бумаг: Учебник / Под ред. В.А. Галанова,
А.И. Басова. – М.: Финансы и статистика, 2002. – 352 с.
6.
Рэй К.И. Рынок ценных бумаг / Пер. с англ. – М.: Дело,
2001. – 587 с.
7.
Фадеев А. Формирование портфеля ценных бумаг. – М.:
ИНФРА-М, 2002. – 391 с.
8.
Ценные бумаги: Учебник / Под ред. В.И. Колесникова,
В.С. Торкановского. – 2-е изд., перераб. и доп. – М.: Финансы и статистика,
2004. – 448 с.
9.
Ценные бумаги:
Учеб. пособие / Н.И. Берзон, М.А. Кожевников, С.Е. Гуськов и др. – М.:
ВШЭ, 2002. – 253 с.
10.
Шихвердиев А.П. Основы рынка ценных бумаг. – Сыктывкар:
Пролог, 2001. – 412 с.
[1] Галанов В.А., Басов А.И. Рынок
ценных бумаг. - М.: Финансы и статистика, 2002. – С. 109
[2] Ценные бумаги: Учебник / Под ред.
В.И. Колесникова. – М.: Финансы и статистика, 2004. – С. 25
[3] Миркин Я.М. Ценные бумаги и фондовый
рынок. – М.: Перспектива, 2000. – С. 96
[4] Буренин А.Н. Рынок ценных бумаг и
производных финансовых инструментов: Учеб. пособие. – М.: Открытое общество,
2002. – С. 133
[5] Рынок ценных бумаг: Учебник / Под
ред. В.А. Галанова, А.И. Басова. – М.: Финансы и статистика, 2002. – С. 189
[6] Рэй К.И. Рынок ценных бумаг/ Пер. с
англ. – М.: Дело, 2001. – С. 215
[7] Ценные бумаги: Учеб. пособие / Н.И.
Берзон, М.А. Кожевников, С.Е. Гуськов и др. – М.: ВШЭ, 2002. – С. 105.