7. Годовая эффективная ставка процента по срочным рублевым вкладам – 11%. Ожидаемый рост курса доллара в течение ближайших 12 месяцев – 13%. Определите, при каких относительных различиях между ценами покупки и продажи в обменных пунктах имеющему доллары и нуждающемуся через год в долларах целесообразно: а) продолжать хранить их в банке, б) закрыть вклад, купить доллары, а через год поменять их на рубли.

Решение.

Пусть n – отношение курса продажи к курсу покупки, k₁ – курс доллара при покупке в начале срока. Тогда курс доллара при продаже в конце срока (через год) будет равен k₁∙n∙1.13.

S – Исходная сумма в долларах. Продав их, мы получим S∙k₁ рублей. Положив их на срочный вклад, в конце года получим S∙k₁∙1.11 рублей. Поменяв рубли на доллары мы получим (S∙k₁∙1.11)/(k₁∙n∙1.13)=(S∙1.11)/(n∙1.13) =S∙0.9823/n долларов.

Т.к. полученное соотношение меньше единицы, то ни при каких условиях данная сделка выгодной не будет, это означает, что выгоднее продолжать хранить деньги в банке.

14. Банк предоставляет рублевые кредиты сроком на 2 года на следующих условиях: расчетная ставка составляет 24% годовых, основной долг необходимо погашать ежемесячно двадцатью четырьмя равными частями с одновременной уплатой процентов за пользование той суммой денег, которую заемщик был должен в течении последнего месяца. На аналогичных условиях, исходя из ставки 12% годовых, предоставляются кредиты в долларах США. Определите денежные суммы, которые: а) необходимо ежемесячно возвращать банку получившему рублевый кредит в размере 1.2 млн. руб.; б) необходимо ежемесячно возвращать банку получившему кредит в долларах на такую же сумму в 1.2 млн. руб.

В случае б) рассчитайте рублевые эквиваленты возвращаемых сумм. В обоих случаях рассчитайте величины 2 первых и двух последних платежей.  На момент получения кредита курс доллара составляет 30 руб., ежемесячно он увеличивается на 0.5%.

Решение.

а) Рассчитаем сумму, которую необходимо вернуть в банк в конце каждого месяца. Эта сумма состоит из двух частей. Первая – часть долга. Она постоянна и составляет 1200000/24=50000 рублей. Вторая – проценты за пользование той суммой денег, которую заемщик был должен в течении последнего месяца. Эта сумма составляет (1200000–50000·(N–1))·0.02, где N – номер прошедшего месяца.

Таким образом, величина платежа после первого месяца составит 50000+1200000·0.02=50000+24000=74000 рублей.

Величина второго платежа составит

50000+(1200000–50000)·0.02=50000+(24000–1000)=73000 рублей.

Величина предпоследнего платежа составит

50000+(1200000–50000·22)·0.02=50000+100000·0.02=52000 рублей.

Величина последнего платежа составит

50000+(1200000–50000·23)·0.02=50000+50000·0.02=51000 рублей.

б) Переведя сумму заема в доллары по начальному курсу получим сумму  в 40000 долларов. Рассчитаем сумму, которую необходимо вернуть в банк в конце каждого месяца. Эта сумма состоит из двух частей. Первая – часть долга. Она постоянна и составляет 40000/24=1666.67 долларов. Вторая – проценты за пользование той суммой денег, которую заемщик был должен в течении последнего месяца. Эта сумма составляет (40000–1666.67·(N–1))·0.01, где N – номер прошедшего месяца.

Для нахождения рублевого эквивалента отдаваемых сумм необходимо умножить сумму в долларах на курс доллара в текущем месяце. Он будет равен 30·(1+0.005)^N, где N – номер прошедшего месяца. Таким образом рублевый эквивалент суммы, отдаваемой после N-го месяца будет равен (1666.67+(40000–1666.67·(N–1))·0.01) ·30·(1+0.005)^N.

Таким образом, величина платежа после первого месяца составит

(1666.67+40000·0.01) = 2066.67 долларов или 2066.67·30·(1+0.005) = 62310.10 рублей

Величина второго платежа составит

(1666.67 + ((40000–1666.67)·0.01)) = 1666.67+383.33 = 2050 долларов или 2050·30·(1+0.005)² = 62116.54 рублей

Величина предпоследнего платежа составит

(1666.67 + ((40000–1666.67·22)·0.01)) = 1666.67+33.33 = 1700 долларов или 1700·30·(1+0.005)²³ = 57199.15 рублей

Величина последнего платежа составит

(1666.67 + ((40000–1666.67·23)·0.01)) = 1666.67+16.67 = 1683.34 долларов или 1683.34·30·(1+0.005)²⁴ = 56921.79 рублей

15. Фирме Х была предоставлена кредитная линия на 2 млн. рублей – в течение 10 месяцев по 1-м числам она брала в банке по 200 тыс. руб. Погашение долга предусматривалось единовременным платежом ровно через 7 месяцев после получения последних 200 тысяч. Сколько должна вернуть фирма банку, если для соизмерения денежных сумм во времени используется годовая эффективная ставка 16%.

Решение.

После получения последнего кредита задолженность фирмы перед банком составляла:

200000∙(1+(1+0.16/12)+(1+0.16/12)²+…+(1+0.16/12)⁹) = по формуле суммы геометрической прогрессии = 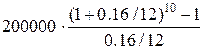 = 2124367.83

После 7 месяцев задолженность составит

2124367.83*(1+0.16/12)⁷=2124367.83*1.097=2330431.51 руб.

17. Рассчитайте формальную рыночную стоимость акций, по которым ежегодно выплачиваются дивиденды в размере 250 руб. на одну акцию. Годовая эффективная ставка процента составляет 13%. Цену рассчитать для момента, когда до получения очередного дивиденда остается ровно 7 месяцев.

Решение.

Стоимость акции сразу после выплаты дивидендов – 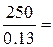1923.08 руб.

В день выплаты дивидендов стоимость акции будет равна 1923.08+250=2173.08 руб.

Для момента, когда до уплаты дивиденда остается семь месяцев, т.е. через 5 месяцев после выплаты стоимость акции составит

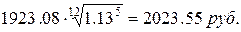
18. При какой годовой эффективной ставке процента на денежном рынке максимальная рыночная стоимость консоли, позволяющей ее владельцу получать ежегодно получать 500 рублей, составит 6000 рублей.

Решение.

Обозначим искомую ставку x. Получим:

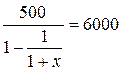
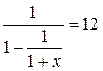
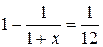
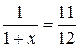
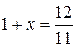
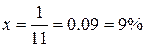
19. С каким дисконтом банк должен учесть вексель, срок погашения которого – через 4.5 месяца, чтобы доходность этой операции была такой же, как при выдаче кредита на такой же срок, исходя из расчетной ставки 18% годовых?

Решение.

Рассчитаем доходность кредита на на 4.5 месяца при расчетной ставке 18% годовых.

0.18∙4.5/12=0.0675=6.75%.

Доходность вексельной операции будет также 6.75%, следовательно с таким дисконтом банк и должен учесть вексель в предлагаемых условиях.