Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное профессиональное учреждение

Высшего профессионального образования

Всероссийский заочный финансово-экономический институт

Филиал в городе Туле

ЛАБОРАТОРНАЯ РАБОТА

По дисциплине: экономико-математические методы и прикладные модели.

Вариант 4

 

          

                                         Выполнил:   студент 3 курса  факультета

                                                                       Менеджмента и маркетинга

                                                                       специальность ГМУ

                                                                       группы дневной

                                                                       

                                                                       № личного дела:        

                                                     

                                                       

                                               Проверил:    

Тула 2009г.

Задача.

     На складах А, В, С и Д находятся соответственно 50т, 40, 40 и 70т муки, которую нужно доставить четырем хлебозаводам. Первому хлебозаводу требуется 50т муки, второму - 40т, третьему - 50т и четвертому - 60т муки. Стоимости доставки одной тонны муки со склада А каждому хлебозаводу соответственно равны 8, 3, 5 и 2 ден. единиц, со склада В - 7, 4, 9, и 8, со склада С - 6, 3, 3 и 1, со склада Д - 2, 4, 1 и 5 ден. единиц. Составить план перевозки муки, обеспечивающий минимальные транспортные расходы.

     Решение:

Поставщики (склады)	Потребители (Хлебозаводы)	Запасы
B1	B2	B3	B4
A	8	3	5	2	50
В	7	4	9	8	40
С	6	3	3	1	40
D	2	4	1	5	70
Потребности	50	40	50	60	200 200

Транспортная задача является закрытой, т.к. потребности потребителей равны объему поставщиков.

Сформулируем экономико-математическую модель исходной транспортной задачи.

F(x) = 8x₁₁ + 3x₁₂ + 5x₁₃ + 2x₁₄ + 7x₂₁ + 4x₂₂ + 9x₂₃ + 8x₂₄ + 6x₃₁ + 3x₃₂ + 3x₃₃ + 1x₃₄ + 2x₄₁ + 4x₄₂ + 1x₄₃ + 5x₄₄  →  min

          Функциональные ограничения для поставщиков:

8x₁₁ + 3x₁₂ + 5x₁₃ + 2x₁₄ ≤ 50

7x₂₁ + 4x₂₂ + 9x₂₃ + 8x₂₄ ≤ 40

6x₃₁ + 3x₃₂ + 3x₃₃ + 1x₃₄ ≤ 40

2x₄₁ + 4x₄₂ + 1x₄₃ + 5x₄₄ ≤ 70

       x _ij ≥ 0

   Функциональные ограничения для потребителей:

8x₁₁ + 7x₂₁ + 6x₃₁ + 2x₄₁ ≤ 50

3x₁₂ + 4x₂₂ + 3x₃₂ + 4x₄₂ ≤ 40

5x₁₃ + 9x₂₃ + 3x₃₃ + 1x₄₃ ≤ 50

2x₁₄ + 8x₂₄ + 1x₃₄ + 5x₄₄ ≤ 60

x _ij ≥ 0

Для получения начального опорного плана воспользуемся методом наименьших стоимостей (наименьшего элемента). В различных модификациях этого метода заполнение клеток матрицы перевозок проводится с учетом значений величин с_ij. Так, в модификации «двойного предпочтения» отмечают клетки с наименьшими стоимостями перевозок сначала по каждой строке, а затем по каждому столбцу. Клетки, имеющие две отметки, заполняют в первую очередь, затем заполняют клетки с одной отметкой, а данные о нераспределенном грузе записывают в неотмеченные клетки с наименьшими стоимостями. При этом из двух клеток с одинаковой стоимостью перевозок предпочтение отдается клетке, через которую осуществляется больший объем перевозок.

Поставщики (склады)	Потребители (Хлебозаводы)	Запасы
B1	B2	B3	B4
A	8	3 30	5	2 20	50
В	7 30	4 10	9	8	40
С	6	3	3	1 40	40
D	2 20	4	1 50	5	70
Потребности	50	40	50	60	200 200

Суммарные затраты на перевозки, представленные в данной таблице составляют: F(x) = 3*30 + 2*20 + 7*30 + 4*10 + 1*40 + 2*20+ 1*50 = 510

Проверим полученный план на оптимальность. Для этого рассчитаем потенциалы поставщиков и потребителей (v_j, u_i) по формуле: v_j = u_i + с_ij следующим образом: задавая u₁ = 0, находим по клетке (1;2) v₂ = 3, по клетке (2;2) u₂ = -1, а по (2;1) v₁ = 6; затем по клетке (1;4) v₄ = 2, а по (3;4) u₃ = 1, по (4;1) находим u₄ = 4 и наконец, по клетке (3;3) находим v₃ = 5.

Поставщики (склады)	Потребители (Хлебозаводы)	Запасы	ui
B1	B2	B3	B4
A	8	-       3 30	5	+     2 20	50	0
В	-       7 30	+       4 10	9	8	40	-1
С	6	3	+      3	-     1 40	40	1
D	+     2 20	4	-       1 50	5	70	4
Потребности	50	40	50	60	200 200
vj	6	3	5	2

На основании рассчитанных потенциалов определяем оценки для всех клеток матрицы перевозок по следующей формуле:

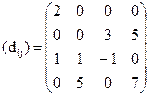
Условием оптимальности распределения служит условие неотрицательности оценок свободных клеток матрицы перевозок. Поскольку в нашем случае имеется отрицательное значение, то это говорит о неоптимальности плана. Для улучшения плана воспользуемся методом потенциалов.

Чтобы улучшить неоптимальный план перевозок, выбирается клетка матрицы перевозок с отрицательной оценкой (в данном случае клетка (3,3)). Для выбранной клетки строим замкнутый контур, начальная вершина которого лежит в выбранной клетке, а все остальные вершины находятся в занятых клетках. В вершинах контура расставляем поочередно знаки «+» и «–», начиная со знака «+» в выбранной свободной клетке.

Величина перераспределяемой поставки определяется как наименьшая из величин поставок в вершинах контура со знаком «–» (клетка (1,2)). На эту величину (30) увеличиваются поставки в вершинах «+» и уменьшаются поставки в вершинах со знаком «–». Если величина перераспределяемой поставки равна поставкам не в одной, а в нескольких вершинах контура со знаком «–», то освобождается только одна клетка, обычно с наибольшей стоимостью перевозки, а все другие такие клетки остаются занятыми с нулевой поставкой.

Результат указанных операций:

Поставщики (склады)	Потребители (Хлебозаводы)	Запасы	ui
B1	B2	B3	B4
A	8	3 0	5	2 50	50	0
В	7	4 40	9	8	40	-1
С	6	3	3 30	1 10	40	1
D	2 50	4	1 20	5	70	3
Потребности	50	40	50	60	200 200
vj	5	3	4	2

Аналогично с первым планом определим  оценки для всех клеток матрицы перевозок:

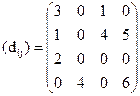
Поскольку отрицательных оценок нет, то план перевозок является оптимальным.

Суммарные затраты на перевозки, при оптимальном плане составляют:

F(x) = 2*50 + 4*40 + 3*30 + 1*10 + 2*50 + 1*20 = 480

Наличие нулевых оценок свободных клеток в оптимальном плане перевозок свидетельствует о неединственности оптимального плана.

Решаем в MS Excel

1.Создаем форму:

Для этого необходимо выполнить резервирование изменяемых ячеек: в блок ячеек В3:Е6 вводится «1». Таким образом, резервируется место, где после решения задачи будет находиться распределение поставок, обеспечивающее минимальные затраты  на перевозку груза.

2.Вводим граничные условия.

Введение условия реализации мощностей поставщиков, т.е.

аi=∑хij

где аi – мощность i-го поставщика

xij – объем поставки груза от i-го поставщика к j-му потребителю

n – количество потребителей.

Для этого необходимо выполнить следующие операции:

- курсор в ячейку А3

- щелкнуть знак «∑»

- выделить необходимые для суммирования ячейки В3:Е3

- нажать ENTER – подтверждение ввода формулы для суммирования.

Аналогичные действия выполняем для ячеек А4, А5, А6.

Введение условия удовлетворения запросов потребителей, т.е.

bj=∑xij

где b – мощность j-го потребителя

m – количество поставщиков.

Для этого необходимо выполнить следующие операции:

- курсор в В7

- щелкнуть знак «∑». При этом автоматически выделяется весь столбец В3:В6

- ENTER – подтверждение суммирования показателей выделенного столбца.

Последовательность этих действий выполнить для ячеек С7 – Е7.

3.Вводим исходные данные.

4.Назначаем целевую функцию.

Для вычисления значения целевой функции необходимо зарезервировать ячейку и ввести формулу для ее вычисления:

F=∑∑CijXij

где Сij – стоимость доставки единицы груза от i-го поставщика к j-му потребителю

Хij – объем поставки груза от i-го поставщика к j-му потребителю.

Для этого:

- курсор в ячейку В15. В данную ячейку будет помещаться значение целевой функции после решения задачи

- щелкнуть Мастер функций

- в окне Категория выбрать Математические

- в окне Функция выбрать СУММПРОИЗВ

- ОК

- в окне СУММПРОИЗВ указать адреса массивов, элементы которых обрабатываются этой функцией.

- в поле Массив 1 указать адреса В11:Е14

- в поле Массив 2 указать адреса В3:Е6

- ОК

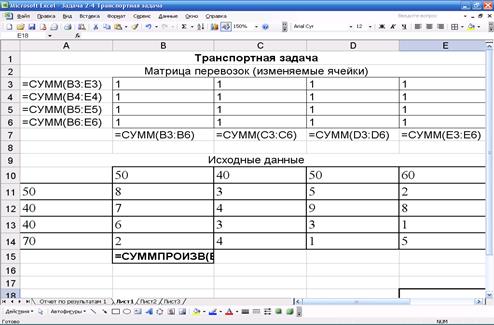
Получаем:

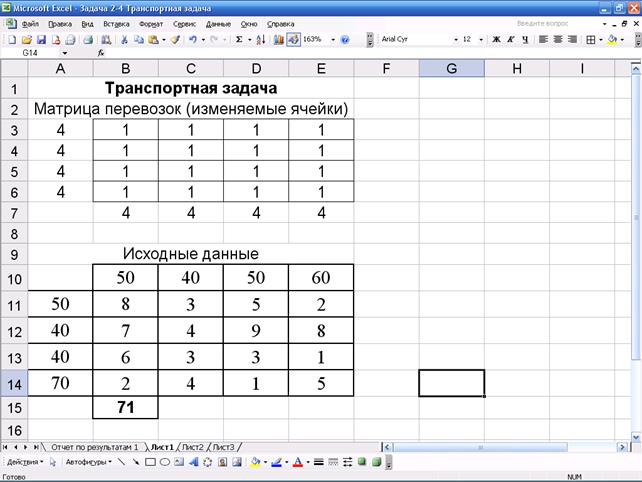
 5.Вводим зависимости из математической модели.

- щелкнуть Сервис – Поиск решения

- курсор подвести в поле Установить целевую (ячейку)

- ввести адрес $B$15

- установить направление изменения целевой функции, равное минимальному значению

- ввести адреса изменяемых ячеек В3:Е6.

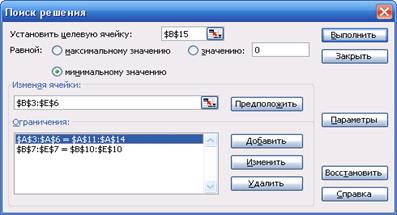
         6.Вводим ограничения:

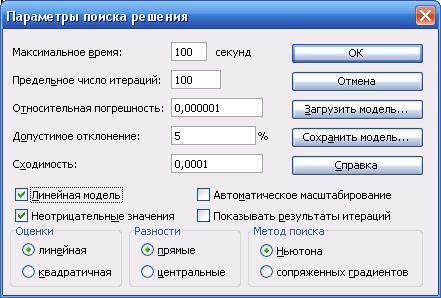
- щелкнуть Параметры

- установить Линейная модель

- установить Неотрицательные значения

- ОК. После этого осуществляется выход в поле Поиска решений

- нажать Выполнить.

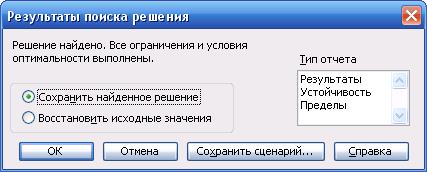
После выполнения всех вышеуказанных действий на экран выводится окно Результаты поиска решения.

В матрице перевозок содержатся оптимальные объемы поставок грузов от поставщика потребителям, дающие минимум затрат на доставку. Значение целевой функции содержится в ячейке В15 и равно 480.

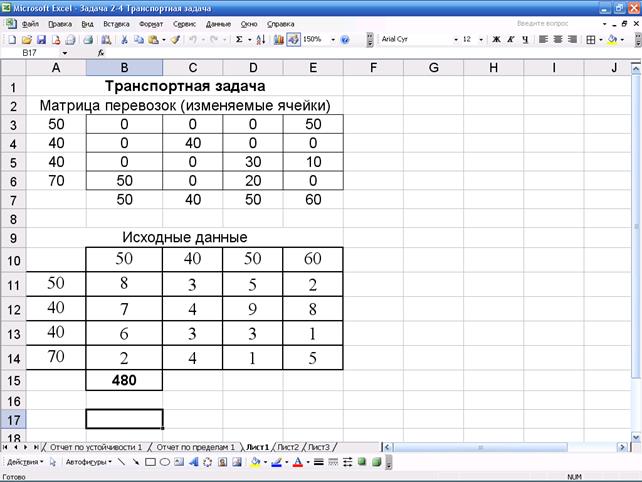
Ответ: Суммарные затраты на перевозки, при оптимальном плане составляют: F(x) = 480