Министерство образования РФ
Всероссийский заочный финансово – экономический институт
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Финансовая
математика»
Вариант №8
Исполнитель: Мартынова Е.И.
Специальность: Финансы и
кредит
Группа: Вечер
№ зачетной книжки:
05ФФБ01928
Руководитель: Филонова Е.С.
Орел
2008
Задание 1.
Приведены поквартальные данные о кредитах от коммерческого банка на
жилищное строительство (в условных единицах) за 4 года (всего 16 кварталов,
первый столбец соответствует первому кварталу первого года).
|
Квартал
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
Данные о кредитах
|
39
|
50
|
59
|
38
|
42
|
54
|
66
|
40
|
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
|
45
|
58
|
69
|
42
|
50
|
62
|
74
|
46
|
Требуется:
1) Построить адаптивную мультипликативную модель Хольта-Уинтерса с
учетом сезонного фактора, приняв параметры сглаживания  = 0,3;
= 0,3;  = 0,6;
= 0,6; 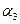 = 0,3.
= 0,3.
2) Оценить точность построенной модели с использованием средней относительной
ошибки аппроксимации.
3) Оценить адекватность построенной модели на основе исследования:
- случайности остаточной компоненты по критерию пиков;
- независимости уровней ряда остатков по d-критерию (критические значения 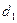 = 1,10 и
= 1,10 и
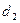 = 1,37)
и по первому коэффициенту автокорреляции при критическом значении
= 1,37)
и по первому коэффициенту автокорреляции при критическом значении 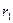 = 0,32;
= 0,32;
- нормальности распределения остаточной компоненты по R/S-критерию с критическими
значениями от 3 до 4,21.
4) Построить точечный прогноз на 4 шага вперед, т.е. на 1 год.
5) Отразить на графике фактические, расчетные и прогнозные данные.
Решение:
1) Построим адаптивную мультипликативную модель Хольта-Уинтерса:
а) Оценка начальных параметров модели –  и
и 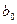 :
:
Для этого применим МНК к первой половине уровней ряда.
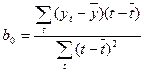 ;
; 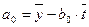
Для удобства расчетов построим таблицу.
Таблица 1.1
|

|
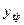
|
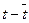
|
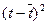
|
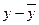
|

|
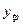
|
|
1
|
39
|
-3,5
|
12,25
|
-9,5
|
33,25
|
45,3
|
|
2
|
50
|
-2,5
|
6,25
|
1,5
|
-3,75
|
46,2
|
|
3
|
59
|
-1,5
|
2,25
|
10,5
|
-15,75
|
47,1
|
|
4
|
38
|
-0,5
|
0,25
|
-10,5
|
5,25
|
48
|
|
5
|
42
|
0,5
|
0,25
|
-6,5
|
-3,25
|
48,9
|
|
6
|
54
|
1,5
|
2,25
|
5,5
|
8,25
|
49,8
|
|
7
|
66
|
2,5
|
6,25
|
17,5
|
43,75
|
50,7
|
|
8
|
40
|
3,5
|
12,25
|
-8,5
|
-29,75
|
51,6
|
|
36
|
388
|
-
|
42
|
-
|
38
|
-
|
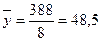 ;
; 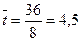
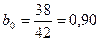 ;
; 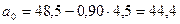
Линейная модель 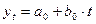 принимает вид:
принимает вид:  .
.
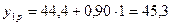 ;
; 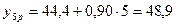 ;
;
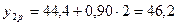 ;
; 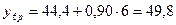 ;
;
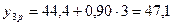 ;
; 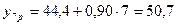 ;
;
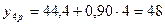 ;
;  .
.
б) Оценка начального
массива сезонных коэффициентов:
Для четырех
кварталов первого года (t = 1) необходимы четыре начальных
значения сезонных коэффициентов. Для их расчета используем формулу:
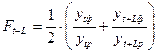
Получаем:
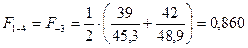 ;
;
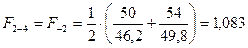 ;
;
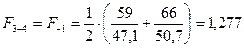 ;
;
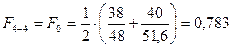 .
.
в) Корректировка
параметров 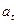 и
и 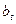 от уровня к уровню:
от уровня к уровню:
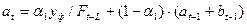 ;
;
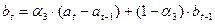 ;
;
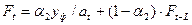 ;
;
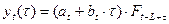 ;
;
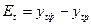 .
.
Для удобства
расчетов построим таблицу.
Таблица
1.2
|
t
|
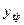
|
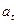
|
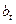
|
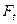
|
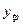
|
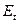
|
|
0
|
-
|
44,40
|
0,90
|
-
|
-
|
-
|
|
1
|
39
|
45,31
|
0,90
|
0,86
|
39,75
|
-0,75
|
|
2
|
50
|
46,20
|
0,90
|
1,08
|
51,01
|
-1,01
|
|
3
|
59
|
46,83
|
0,82
|
1,27
|
60,85
|
-1,85
|
|
4
|
38
|
47,92
|
0,90
|
0,79
|
38,22
|
-0,22
|
|
5
|
42
|
48,81
|
0,90
|
0,86
|
42,77
|
-0,77
|
|
6
|
54
|
49,76
|
0,91
|
1,08
|
54,86
|
-0,86
|
|
7
|
66
|
51,11
|
1,04
|
1,28
|
66,05
|
-0,05
|
|
8
|
40
|
51,71
|
0,91
|
0,78
|
41,52
|
-1,52
|
|
9
|
37
|
49,74
|
0,05
|
0,79
|
42,83
|
-5,83
|
|
10
|
48
|
48,13
|
-0,45
|
1,03
|
51,69
|
-3,69
|
|
11
|
57
|
46,72
|
-0,74
|
1,24
|
58,93
|
-1,93
|
|
12
|
35
|
45,65
|
-0,84
|
0,77
|
34,94
|
0,06
|
|
13
|
42
|
47,31
|
-0,09
|
0,85
|
37,33
|
4,67
|
|
14
|
52
|
48,17
|
0,20
|
1,06
|
49,92
|
2,08
|
|
15
|
62
|
48,80
|
0,33
|
1,26
|
61,15
|
0,85
|
|
16
|
39
|
49,55
|
0,45
|
0,78
|
38,59
|
0,41
|
Для t = 1:
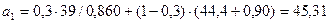 ;
;
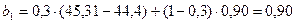 ;
;
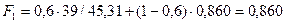 ;
;
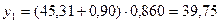 ;
;
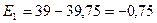 .
.
Для t = 2:
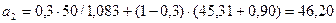 ;
;
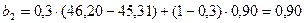 ;
;
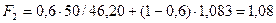 ;
;
 ;
;
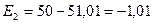 .
.
Для t = 3:
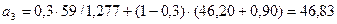 ;
;
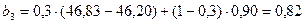 ;
;
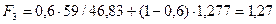 ;
;
 ;
;
 .
.
Для t = 4:
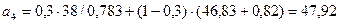 ;
;
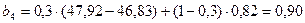 ;
;
 ;
;
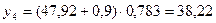 ;
;
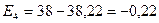 .
.
Для t = 5:
 ;
;
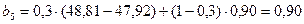 ;
;
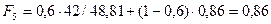 ;
;
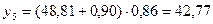 ;
;
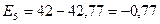 .
.
и т.д.
Таблицу расчетных значений
показателя и ошибок, полученную в результате обработки данных в ППП Олимп см. в
Приложение 1.
Таким образом, на
последнем шаге получаем адаптивную мультипликативную модель Хольта-Уинтерса
вида: 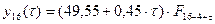
2) Оценим точность построенной модели с
использованием средней относительной ошибки аппроксимации:
Для удобства расчетов построим таблицу.
Таблица
2.1
|
t
|
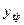
|
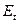
|
Точки поворота
|
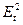
|
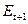
|
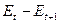
|
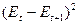
|
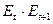
|
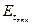
|
|
1
|
39
|
-0,75
|
-
|
0,56
|
-1,01
|
0,26
|
0,07
|
0,76
|
1,9
|
|
2
|
50
|
-1,01
|
1
|
1,02
|
-1,85
|
0,84
|
0,71
|
1,87
|
2
|
|
3
|
59
|
-1,85
|
0
|
3,42
|
-0,22
|
-1,63
|
2,66
|
0,41
|
3,1
|
|
4
|
38
|
-0,22
|
1
|
0,05
|
-0,77
|
0,55
|
0,30
|
0,17
|
0,6
|
|
5
|
42
|
-0,77
|
1
|
0,59
|
-0,86
|
0,09
|
0,01
|
0,66
|
1,8
|
|
6
|
54
|
-0,86
|
0
|
0,74
|
-0,05
|
-0,81
|
0,66
|
0,04
|
1,6
|
|
7
|
66
|
-0,05
|
0
|
0,00
|
-1,52
|
1,47
|
2,16
|
0,08
|
0,1
|
|
8
|
40
|
-1,52
|
1
|
2,31
|
-5,83
|
4,31
|
18,58
|
8,86
|
3,8
|
|
9
|
37
|
-5,83
|
0
|
33,99
|
-3,69
|
-2,14
|
4,58
|
21,51
|
15,8
|
|
10
|
48
|
-3,69
|
1
|
13,62
|
-1,93
|
-1,76
|
3,10
|
7,12
|
7,7
|
|
11
|
57
|
-1,93
|
1
|
3,72
|
0,06
|
-1,99
|
3,96
|
-0,12
|
3,4
|
|
12
|
35
|
0,06
|
1
|
0,00
|
4,67
|
-4,61
|
21,25
|
0,28
|
0,2
|
|
13
|
42
|
4,67
|
0
|
21,81
|
2,08
|
2,59
|
6,71
|
9,71
|
11,1
|
|
14
|
52
|
2,08
|
1
|
4,33
|
0,85
|
1,23
|
1,51
|
1,77
|
4
|
|
15
|
62
|
0,85
|
1
|
0,72
|
0,41
|
0,44
|
0,19
|
0,35
|
1,4
|
|
16
|
39
|
0,41
|
-
|
0,17
|
-
|
-
|
-
|
-
|
1,1
|
|
Сумма
|
|
-10,41
|
р=9
|
87,06
|
|
|
66,44
|
53,47
|
59,6
|
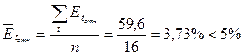 , следовательно, уровень точности модели является
достаточным. Фактические данные отличаются от расчетных, в среднем, на 3,73%.
, следовательно, уровень точности модели является
достаточным. Фактические данные отличаются от расчетных, в среднем, на 3,73%.
3) Оценим адекватность построенной модели:
а) Свойство случайности уровней
в ряде остатков:
Для проверки данного
свойства используют критерий поворотных точек. Общее число поворотных точек
равно p = 9 (см. Таблицу 2.1). Свойство случайности
выполняется если количество поворотных точек р удовлетворяет неравенству р
> [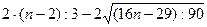 ].
].
9 > [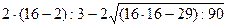 ]
]
9 > [6,2]
p = 9 > 6, следовательно, свойство
случайности уровней в ряде остатков выполняется.
б) Свойство независимости уровней в ряде
остатков или отсутствия автокорреляции:
Данное свойство
проверим двумя методами:
I) по d-критерию
Дарбина-Уотсона;
II) по первому коэффициенту
автокорреляции r(1).
I) 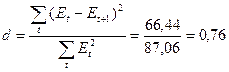
При  и
и  :
:
d 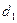
| |
| |
| | 
0 0,76 1,10 1,37 2 4
Так как d попало в промежуток (0;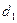 ), то свойство независимости уровней в ряде остатков не выполняется,
остатки автокоррелируют.
), то свойство независимости уровней в ряде остатков не выполняется,
остатки автокоррелируют.
II) 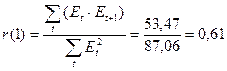
Так как 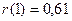 >
> 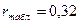 , то свойство независимости уровней в ряде остатков не
выполняется, остатки автокоррелируют.
, то свойство независимости уровней в ряде остатков не
выполняется, остатки автокоррелируют.
в) Свойство соответствия ряда остатков
нормальному закону распределения:
Для проверки данного
свойства применяют RS-критерий.
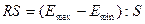 ;
; 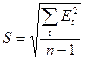
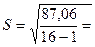
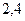
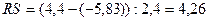
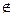 (3; 4,21), следовательно, свойство соответствия ряда
остатков нормальному закону распределения не выполняется.
(3; 4,21), следовательно, свойство соответствия ряда
остатков нормальному закону распределения не выполняется.
г) Свойство равенства нулю математического
ожидания:
Так как  (см. Таблицу 2.1), следовательно, свойство равенства нулю
математического ожидания не выполняется.
(см. Таблицу 2.1), следовательно, свойство равенства нулю
математического ожидания не выполняется.
Вывод: так как не
все свойства выполнены, то построенная модель является не адекватной.
4) Построим точечный
прогноз на 4 шага вперед, т.е. на 1 год:
Прогноз выполняется
по формуле: 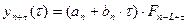 . Для прогноза используем модель полученную на последнем шаге
расчетов, то есть
. Для прогноза используем модель полученную на последнем шаге
расчетов, то есть 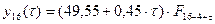 .
.
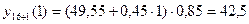
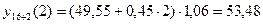


5) Отразим на
графике фактические, расчетные и прогнозные данные:
Для построения
графика используем ППП Олимп (см. Приложение 2).
Задание 2.
Выполнить различные коммерческие расчеты, используя данные, приведенные
в таблице. В условии задачи значения
параметров приведены в виде переменных. Например, S означает некую сумму средств в рублях,  – время
в годах, i –
ставку в процентах и т.д. По именам переменных из таблицы необходимо выбрать
соответствующие численные значения параметров и выполнить расчеты.
– время
в годах, i –
ставку в процентах и т.д. По именам переменных из таблицы необходимо выбрать
соответствующие численные значения параметров и выполнить расчеты.
|
Сумма
|
Дата
начальная
|
Дата конечная
|
Время в
днях
|
Время в
годах
|
Ставка
|
Число начислений
|
|
S
|
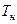
|
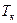
|
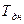
|
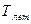
|
i
|
m
|
|
4000000
|
10.01.02
|
20.03.02
|
90
|
5
|
45
|
4
|
2.1. Банк выдал ссуду, размером S руб. Дата выдачи ссуды – 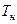 , возврата –
, возврата – 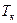 . День
выдачи и день возврата считать за 1 день. Проценты рассчитываются по простой
процентной ставке i% годовых. Найти:
. День
выдачи и день возврата считать за 1 день. Проценты рассчитываются по простой
процентной ставке i% годовых. Найти:
2.1.1) точные проценты с точным
числом дней ссуды;
2.1.2) обыкновенные проценты с точным числом дней ссуды;
2.1.3) обыкновенные проценты с приближенным числом дней ссуды.
2.2. Через 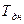 дней после подписания договора
должник уплатит S руб. Кредит выдан
под i% годовых (проценты
обыкновенные). Какова первоначальная сумма и дисконт?
дней после подписания договора
должник уплатит S руб. Кредит выдан
под i% годовых (проценты
обыкновенные). Какова первоначальная сумма и дисконт?
2.3. Через 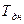 дней предприятие должно получить по
векселю S руб. Банк приобрел этот
вексель с дисконтом. Банк учел вексель по учетной ставке i% годовых (год равен 360 дням).
Определить полученную предприятием сумму и дисконт.
дней предприятие должно получить по
векселю S руб. Банк приобрел этот
вексель с дисконтом. Банк учел вексель по учетной ставке i% годовых (год равен 360 дням).
Определить полученную предприятием сумму и дисконт.
2.4. В кредитном договоре на сумму S
руб. и сроком на 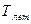 лет, зафиксирована ставка сложных
процентов, равная i% годовых.
Определить наращенную сумму.
лет, зафиксирована ставка сложных
процентов, равная i% годовых.
Определить наращенную сумму.
2.5. Ссуда, размером S руб.
предоставлена на 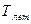 . Проценты
сложные, ставка – i% годовых. Проценты
начисляются т раз в году. Вычислить наращенную сумму.
. Проценты
сложные, ставка – i% годовых. Проценты
начисляются т раз в году. Вычислить наращенную сумму.
2.6. Вычислить эффективную ставку процента, если банк начисляет проценты
т раз в году, исходя из номинальной ставки i% годовых.
2.7. Определить, какой должна быть номинальная ставка при начислении
процентов т раз в году, чтобы обеспечить эффективную ставку i% годовых.
2.8. Через Тлет предприятию будет выплачена сумма S
руб. Определить ее современную стоимость при условии, что применяется
сложная процентная ставка i% годовых.
2.9. Через Тлет
по векселю должна быть выплачена сумма S руб. Банк учел вексель по
сложной учетной ставке i% годовых.
Определить дисконт.
2.10. В течение Тлеm лет
на расчетный счет в конце каждого года поступает по S руб., на которые т раз в году начисляются проценты по
сложной годовой ставке i%. Определить сумму
на расчетном счете к концу указанного срока.
Решение:
 2.1. Дано: Решение:
2.1. Дано: Решение:
Р
= 4000000 руб. Используем формулу для расчета процентов (процентных
денег): 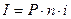 .
.
 10.01.02 Так как продолжительность ссуды
менее года
10.01.02 Так как продолжительность ссуды
менее года 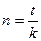 .
.
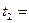 20.03.02 Получаем:
20.03.02 Получаем: 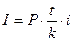 .
.
i = 45% = 0,45 

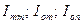 - ?
- ? 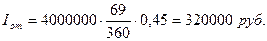
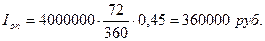
Ответ: 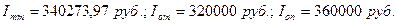
 2.2. Дано:
Решение:
2.2. Дано:
Решение:
S = 4000000 руб. Используем формулу математического
дисконтирования
 90 по простым процентным
ставкам:
90 по простым процентным
ставкам: 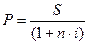 .
.
 i = 45% = 0,45 Так как продолжительность ссуды
менее года
i = 45% = 0,45 Так как продолжительность ссуды
менее года 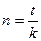 .
.
 - ? Получаем:
- ? Получаем: 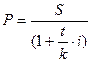 . а) Для k = 360:
. а) Для k = 360: 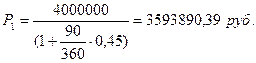
б) Для k =
365: 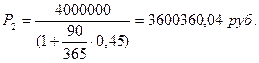
Для
расчета дисконта используем формулу:  .
.
а) 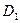 = 4000000-3593890,39 =
406109,61 руб.
= 4000000-3593890,39 =
406109,61 руб.
б)  = 4000000-3600360,04 =
399639,96 руб.
= 4000000-3600360,04 =
399639,96 руб.
Ответ: 
 2.3. Дано:
Решение:
2.3. Дано:
Решение:
S = 4000000 руб. Используем формулу банковского учета по
простым
 90 процентным
ставкам:
90 процентным
ставкам: 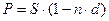 .
.
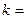 360 Так как продолжительность
ссуды менее года
360 Так как продолжительность
ссуды менее года 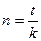 .
.
d = 45% = 0,45 Получаем: 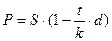 .
.

 - ?
- ? 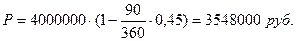
Для
расчета дисконта используем формулу:  .
.
D
= 4000000 – 3548000 = 452000 руб.
Ответ: 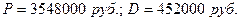
 2.4. Дано: Решение:
2.4. Дано: Решение:
P = 4000000 руб.
Используем формулу наращения по сложным процентам:  .
.
 5
5 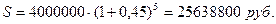
 i = 45% = 0,45
i = 45% = 0,45
S - ?
Ответ: 
 2.5. Дано:
Решение:
2.5. Дано:
Решение:
Используем формулу начисления процентов по номи-
P = 400000 руб нальной
процентной ставке:  .
.
 5
5 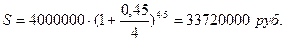
j = 45% = 0,45
 m = 4
m = 4
S - ?
Ответ: 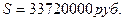
 2.6. Дано:
Решение:
2.6. Дано:
Решение:
m = 4 Используем формулу для расчета
эффективной ставки
 j = 45% = 0,45 процента:
j = 45% = 0,45 процента:
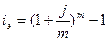 .
.
 -
?
-
? 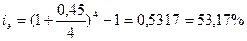
Ответ: 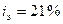
 2.7. Дано:
Решение:
2.7. Дано:
Решение:
m = 4 Используем формулу для
расчета номинальной ставки
 = 45% = 0,45
процента:
= 45% = 0,45
процента:  .
.
 j - ?
j - ?
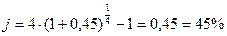
Ответ: 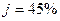
 2.8. Дано:
Решение:
2.8. Дано:
Решение:
S = 4000000 руб.
Используем формулу математического дисконтирования
 5
по сложным процентным
ставкам:
5
по сложным процентным
ставкам: 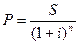 .
.
 i = 45% =
0,45
i = 45% =
0,45 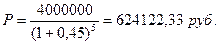
P - ?
Ответ: 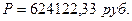
 2.9. Дано:
Решение:
2.9. Дано:
Решение:
S = 4000000 руб.
Используем формулу банковского учета по сложным
 5 процентным ставкам:
5 процентным ставкам: 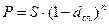 .
.

 = 45% = 0,45
= 45% = 0,45 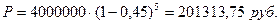
D - ? Для
расчета дисконта используем формулу:  .
.
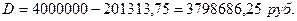
Ответ: 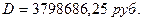
 2.10. Дано:
Решение:
2.10. Дано:
Решение:
R = 4000000 руб. Используем формулу для расчета годовой
ренты с начис-
n = 5 лением процентов m раз в
году: 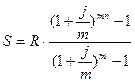 .
.
j = 45% = 0,45 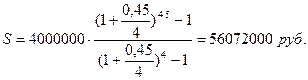
 m=4
m=4
S - ?
Ответ: 
Приложение 1
Таблица расчетных значений показателя и
ошибок, полученная в результате обработки данных в ППП Олимп
|
Номер
|
Факт
|
Расчет
|
Ошибка
абс.
|
Ошибка
относит.
|
|
1
|
39,000
|
39,513
|
-0,513
|
-1,316
|
|
2
|
50,000
|
50,280
|
-0,280
|
-0,560
|
|
3
|
59,000
|
59,044
|
-0,044
|
-0,075
|
|
4
|
38,000
|
37,924
|
0,076
|
0,199
|
|
5
|
42,000
|
40,639
|
1,361
|
3,240
|
|
6
|
54,000
|
53,150
|
0,850
|
1,574
|
|
7
|
66,000
|
63,521
|
2,479
|
3,756
|
|
8
|
40,000
|
41,995
|
-1,995
|
-4,988
|
|
9
|
45,000
|
44,907
|
0,093
|
0,208
|
|
10
|
58,000
|
57,413
|
0,587
|
1,011
|
|
11
|
69,000
|
69,196
|
-0,196
|
-0,284
|
|
12
|
42,000
|
42,664
|
-0,664
|
-1,581
|
|
13
|
50,000
|
47,468
|
2,532
|
5,064
|
|
14
|
62,000
|
62,603
|
-0,603
|
-0,973
|
|
15
|
74,000
|
74,429
|
-0,429
|
-0,580
|
|
16
|
46,000
|
45,592
|
0,408
|
0,887
|
|
Период сезонности =
4
|
|
|
|
|
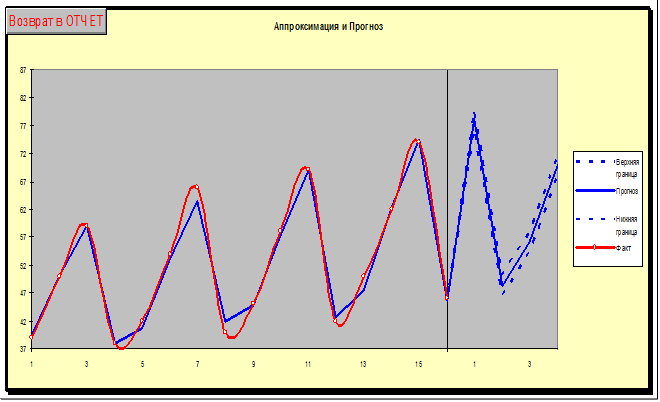
Приложение 2
График фактических, расчетных и
прогнозных данных
Дата сдачи:
Подпись: