Содержание
Задание
1. 2
Задание 2. 3
Задание 3. 4
Задание 4. 5
Задание 5. 8
Задание 6. 11
Список
использованной литературы.. 16
ВАРИАНТ 6
Задание 1
Вероятность того, что студент сдаст в сессию первый экзамен
равна 0.93, второй – 0.83, третий – 0.87. Найти вероятность того, что данный
студент:
а) сдаст только один экзамен; b) сдаст два экзамена;
с) сдаст не менее двух экзаменов; d) сдаст хотя бы один экзамен;
е) все экзамены либо сдаст, либо завалит.
Решение:
p1=0,93; p2=0,83; p3=0,87
Соответственно:
q1=0,07;
q2=0,17; q3=0,13
k –
число сданных экзаменов
а) Студент сдаст только один
экзамен, если не сдаст два других. Таких случаев три, значит вероятность равна:
Р(k=1)=0,93*0,17*0,13+0,07*0,83*0,13+0,07*0,17*0,87=0,03846
b) сдаст
два экзамена:
Р(k=2)=0,93*0,83*0,13+0,07*0,83*0,87+0,93*0,17*0,87=0,28844
с) сдаст не менее двух экзаменов:
Р(k>=2)=
Р(к=2)+Р(к=3)=0,28844+0,93*0,83*0,87=0,95999
d) сдаст хотя бы один экзамен:
Р(k>=1)=1-
Р(к=0)=1-0,07*0,17*0,13=0,99845
е) все экзамены либо сдаст, либо
завалит:
Р(k=3
или k=0)=1- Р(k=1)- Р(k=2)=1-0,03846-0,28844=0,6731
Задание 2
Имеются две партии, содержащие 13 и 18 одинаковых изделий. В
первой партии 6, во второй – 9 бракованных изделий, а остальные изделия
стандартные. Из первой партии во вторую наудачу перекладывают два изделия.
после чего из второй партии также наудачу одновременно берут два изделия.
1.
Определить вероятность того, что, по крайней мере, одно
изделие, взятое из второй партии, окажется стандартным.
2.
Из двух изделий, взятых из второй партии, одно
оказалось бракованным, а другое – стандартным. Какие изделия вероятнее всего
переложили из первой партии во вторую?
Решение:
N1=13, N2=18 – всего
изделий;
m1=6, m2=9 – число
бракованных изделий;
n1=7, n2=9 – число
стандартных изделий;
Рассчитаем вероятность попадания
стандартного изделия из второй партии после перекладывания:
p=2/13 * 7/13 + 9/18=0,583
Вероятность обратного (попадания
бракованного изделия):
q=1-p=0,417
k – число стандартных изделий среди 2-х
выбранных из второй партии
Используя формулу Бернулли Pn(k)=Ckn*pk*qn-k рассчитаем:
1. вероятность того, что, по крайней
мере, одно изделие, взятое из второй партии, окажется стандартным:
P(k>=1)=1-P(k=0)=1-C20*0,5830*0,4172=0,826
2. вероятность того, что из двух
изделий, взятых из второй партии, одно оказалось бракованным, а другое –
стандартным:
P(k=1)= C21*0,5831*0,4171=0,486
Вероятность того, что переложили
из первой партии во вторую стандартную деталь, равная 7/13, больше вероятности
того, что переложили бракованную, равной 6/13.
Задание 3
В некотором автопарке ежедневно в среднем 97% автомобилей
исправны.
1. Какова
вероятность того, что среди 8 наудачу выбранных автомобилей неисправных будет:
а) ровно 6;
b)
не менее 6;
с) не более 6;
d)хотя
бы один автомобиль?
2. Вычислить
вероятность того, что в данном автопарке, имеющем сто автомобилей, в наудачу
выбранный день неисправным будет:
а) 3;
b) более
3;
с) менее 3;
d) хотя
бы один автомобиль.
Решение:
р=1-0,97=0,03 – вероятность попадания неисправного
автомобиля
1. n=8 – число выбранных
автомобилей
k – число неисправных среди выбранных
Используя формулу Бернулли Pn(k)=Ckn*pk*qn-k рассчитаем
вероятности:
а) Р(k=6)= C86*0,036*0,972=0,01921*10-6
b) Р(k>=6)= Р(k=6)+
Р(k=7)+ Р(k=8)=
=0,01921*10-6 +C87*0,037*0,971+
C88*0,038*0,970=0,01938*10-6
с) Р(k<=6)=1- Р(k>=6)+ Р(k=6)=1-0,01938*10-6 +0,01921*10-6=0,99983
d) P(k>=1)=1- P(k=0)=1- C80*0,030*0,978=0,21626
2. .
n=100– число выбранных
автомобилей
k – число неисправных среди выбранных
a) Р(k=3)= C1003*0,033*0,9797=0,227
b) Р(k>3)=1-( Р(k=3)+
Р(k=2)+ Р(k=1)+ Р(k=0))=
=1- (Р(k=3)+ C1002*0,032*0,9798 +
C1001*0,031*0,9799 +C1000*0,030*0,97100)
=1-0,647=0,353
c) Р(k<3)=1- Р(k>3)- Р(k=3)=1-0,353-0,227=0,42
d) P(k>=1)= 1-
P(k=0) = 1- C1000*0,030*0,97100=0,952
Задание 4
В рекламных целях торговая фирма вкладывает в каждую 6-ю
единицу товара денежный приз размером 100 руб. Рассматривается случайная
величина (с.в.) ξ – размер выигрыша при четырех покупках продукции данной
фирмы.
1. Составить ряд распределения с.в. ξ и представить его
графически.
2. Найти функцию распределения с.в. ξ и построить его
график.
3. Вычислить математическое ожидание (среднее значение) М
ξ, дисперсию D
ξ и среднее квадратическое (стандартное) отклонение σ (ξ).
4. Определите вероятности:
а) Р {ξ < М ξ };
b) Р
{ξ < М ξ +1};
c) Р
{|ξ - М ξ| < σ (ξ)}.
Решение:
1. n=4 – число купленных товаров
k – число выигрышных товаров среди
купленных
p=1/6
– вероятность попадания выигрышного товара
q=5/6
– вероятность не попадания выигрышного товара
Р (k=0)
= C40*(1/6)0*(5/6)4=0,4823
Р (k=1)
= C41*(1/6)1*(5/6)3=0,3858
Р (k=2)
= C42*(1/6)2*(5/6)2=0,1157
Р (k=3)
= C43*(1/6)3*(5/6)1=0,0154
Р (k=4)
= C44*(1/6)4*(5/6)0=0,0008
Ряд распределения с.в. ξ:
|
ξ
|
Р
|
|
0
|
0,4823
|
|
100
|
0,3858
|
|
200
|
0,1157
|
|
300
|
0,0154
|
|
400
|
0,0008
|
|
|
1
|
и его графическое представление:
2. Функция распределения с.в. ξ:
F(x)=P(X-x)
|
F(x)
|
x
|
|
0
|
x<=0
|
|
0,4823
|
0<x<=100
|
|
0,8681
|
100<x<=200
|
|
0,9838
|
200<x<=300
|
|
0,9992
|
300<x<=400
|
|
1
|
x>400
|
Его графическое представление:
3.
|
ξ
|
Р
|
ξ *Р
|
ξ2
|
ξ2* Р
|
|
0
|
0,4823
|
0
|
0
|
0
|
|
100
|
0,3858
|
38,58
|
10000
|
3858
|
|
200
|
0,1157
|
23,14
|
40000
|
4628
|
|
300
|
0,0154
|
4,62
|
90000
|
1386
|
|
400
|
0,0008
|
0,32
|
160000
|
128
|
|
Сумма:
|
1
|
66,66
|
-
|
10000
|
Математическое ожидание (среднее значение):
М ξ=∑ξ *Р=66,66
Дисперсия:
D
ξ= М (ξ2) – (М ξ)2=∑ ξ2* Р - (М ξ)2=10000-66,662=5556,44
Среднее квадратическое (стандартное отклонение):
σ(ξ)=√Dξ=√5556,44=74,54
4. а) Р {ξ < М ξ }= Р
{ξ < 66,66}= Р (ξ =0)= 0,4823
b) Р
{ξ < М ξ +1}= Р {ξ < 166,66}= Р (ξ =0)+ Р (ξ
=100)=
=0,4823+0,3858=0,8681
c) Р
{|ξ - М ξ| < σ (ξ)}= Р {|ξ – 66,66| < 74,54}= Р
(ξ =0)+ Р (ξ =100)=
=0,4823+0,3858=0,8681
Задание 5
Время ξ (в годах) безотказной работы электроннолучевой
трубки телевизора является случайным с плотностью распределения:
p(x)=
c*e-x/17, если x>=0
0, если x<0
1. Установить неизвестную постоянную
С и построить график функции p(x).
2. Найти функцию распределения с.в.
ξ и построить ее график.
3. Вычислить математическое ожидание
(среднее значение) М ξ, дисперсию D ξ и среднее квадратическое
(стандартное) отклонение σ (ξ).
4. Во сколько раз число
электроннолучевых трубок со временем безотказной работы больше среднего
превышает число трубок со временем безотказной работы меньше среднего?
Решение:
1. Для определения коэффициента С
воспользуемся формулой:
-∞+∞∫f(x)dx=1
Так как f(x) на разных интервалах задана различными выражениями, то
интеграл -∞+∞∫f(x)dx
разбиваем на два интервала:
-∞+∞∫f(x)dx=-∞0∫0dx+0+∞∫С*e-x/17dx=1
Отсюда 0+∞∫С*e-x/17dx=1
-17*С* e-x/17│0+∞=1
17*С=1
Следовательно: С=1/17
В силу этого плотность
вероятности запишется:
p(x)=
e-x/17/17, если x>=0
0, если x<0
2. Чтобы найти функцию распределения
с.в. ξ используем формулу:
F(x)= -∞x∫f(x)dx
Если x<=0, то f(x)=0, следовательно,
F(x)= -∞x∫0dx=0
Если x>0, то
F(x)= -∞0∫0dx + 0x∫ e-x/17/17
dx= 0x∫e-x/17/17
dx= -e-x/17│0x=1- e-x/17
Итак:
F(x)= 1- e-x/17, если x>=0
0, если x<0
3. Воспользуемся формулами:
M(X)= -∞+∞∫x*f(x) dx и D(X)= -∞+∞∫x2*f(x) dx – [M(X)]2;
M(X)= -∞+∞∫x*f(x) dx=-∞0∫0dx+0+∞∫x*e-x/17 /17dx= -x*e-x/17 -17*e-x/17│0+∞=17
D(X)= -∞+∞∫x2*f(x) dx – 172=-∞0∫x2*0dx+0+∞∫x2*e-x/17 /17dx-172=
-x2*e-x/17 -34x*e-x/17 - 578e-x/17│0+∞-172=578-172=289
Cреднее квадратическое (стандартное) отклонение σ (ξ):
σ
(x)= √D(X)=17
4. Вероятность того, что время
безотказной работы будет меньше среднего:
р(x<17)= -∞17∫f(x)dx=017∫ e-x/17/17
dx =-e-x/17│017=1-е-1
и больше среднего:
р(x>17)= -∞17∫f(x)dx=17∞∫ e-x/17/17
dx = -e-x/17│17∞= е-1
Значит, число электроннолучевых
трубок со временем безотказной работы больше среднего превышает число трубок со
временем безотказной работы меньше среднего в:
р(x>17)/ р(x<17)=
(1-е-1)/ е-1=е-1=1,71828 раз
Задание 6
Исследуется диаметр горошин перед контрольными посевами.
Выборочное обследование горошин дало следующие результаты (в мм):
9.409, 8.642, 9.575, 9.078, 8.505, 10.902, 8.205, 7.836, 9.512, 8.050,
8.869, 9.904, 8.742, 8.467, 8.502, 10.083, 8.377, 8.193, 9.703, 8.607, 9.636,
9.735, 9.619, 9.317, 9.159.
Необходимо:
1. Определить
исследуемый признак и его тип (дискретный или непрерывный).
2. В зависимости
от типа признака построить полигон или гистограмму относительных частот.
3. На основе
визуального анализа полигона (гистограммы) сформулировать гипотезу о законе
распределения признака.
4. Вычислить
выборочные характеристики изучаемого признака: среднее, дисперсию, среднее
квадратическое (стандартное) отклонение.
5. Используя
критерий согласия «хи-квадрат» Пирсона, проверить соответствие выборочных
данных выдвинутому в п.3 закону распределения при уровне значимости 0,01.
6. Для
генеральной средней и дисперсии построить доверительные интервалы,
соответствующие доверительной вероятности 0,99.
7. С надежностью
0,99 проверить гипотезу о равенстве:
а) генеральной
средней значению 9,2;
б) генеральной
дисперсии значению 1,653.
Решение:
1. Тип исследуемого признака непрерывный, т.к. все значения
встречаются ровно по одному разу и распределены в интервале от 7 до 11мм
2. Т.к. тип признака непрерывный, то весь интервал, в
котором заключены все наблюдаемые значения признака разобьем на ряд частичных
интервалов длины h=1 и
найдем mi – сумму частот вариант, попавших в i-й интервал:
|
Номер интервала
i
|
Частичный
интервал
xi-1 - xi
|
Частоты
mi
|
Относительные
частоты
wi= mi /∑mi
|
|
1
|
7,000-8,000
|
1
|
0,04
|
|
2
|
8,001-9,000
|
11
|
0,44
|
|
3
|
9,001-10,000
|
11
|
0,44
|
|
4
|
10,001-11,000
|
2
|
0,08
|
|
Сумма:
|
-
|
25
|
1
|
Т.к. h=1,
то плотности частот равны соответствующим относительным частотам. Построим
гистограмму:
3. На основе визуального
анализа гистограммы можно сделать предположение
о нормальном распределении признака, т.е.:
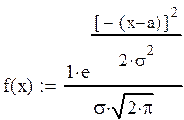
где а –
математическое ожидание, σ
– среднее квадратическое ожидание.
4. Серединные
значения интервалов рассчитаны как xi*= (xi+ xi-1)/2
|
Номер интервала
i
|
Середины частичных интервалов
xi*
|
Сумма частот вариант частичного интервала
mi
|
xi**mi
|
xi* 2
|
xi* 2* mi
|
|
1
|
7,5
|
1
|
7,5
|
56,25
|
56,25
|
|
2
|
8,5
|
11
|
93,5
|
72,25
|
794,75
|
|
3
|
9,5
|
11
|
104,5
|
90,25
|
992,75
|
|
4
|
10,5
|
2
|
21
|
110,25
|
220,5
|
|
Сумма:
|
-
|
25
|
226,5
|
-
|
2064,25
|
Вычислим выборочные характеристики изучаемого
признака: среднее значение (MX)
, дисперсию, среднее квадратическое (стандартное) отклонение:
xсрвыб = ∑ xi**mi /n=226,5/25=9,06
Dвыб= x*2cp
-xсрвыб 2=∑ xi*2* mi / n - xсрвыб 2=82,57-9,062=0,49
σвыб=√0,49=0,70
5. Найдем
исправленную выборочную дисперсию s2:
s2=n/n-1 * Dвыб=25/24 * 0,49=0,507
и исправленное
выборочное среднее квадратическое отклонение:
s=0,712
Найдем
теоретические частоты mi′:
mi′=n*h/s *φ(ti*)=25*1/0,71*φ(ti*)=35,12*φ(ti*),
где ti*= (xi*- xсрвыб)/s
Составим расчетную таблицу
для нахождения теоретических частот:
|
i
|
xi*
|
ti*= (xi*- xсрвыб)/s
|
φ(ti*)[1]
|
mi′=n*h/s *φ(ti*)
|
|
1
|
7,5
|
-2,19
|
0,0363
|
1,27
|
|
2
|
8,5
|
-0,79
|
0,292
|
10,26
|
|
3
|
9,5
|
0,62
|
0,3312
|
11,63
|
|
4
|
10,5
|
2,02
|
0,0519
|
1,82
|
Затем составим расчетную таблицу для вычисления наблюдаемого
значения критерия χ2набл.:
|
i
|
mi
|
mi′
|
mi - mi′
|
(mi - mi′)2
|
(mi - mi′)2/ mi′
|
|
1
|
1
|
1,27
|
-0,27
|
0,08
|
0,06
|
|
2
|
11
|
10,26
|
0,74
|
0,55
|
0,05
|
|
3
|
11
|
11,63
|
-0,63
|
0,40
|
0,03
|
|
4
|
2
|
1,82
|
0,18
|
0,03
|
0,02
|
|
∑
|
-
|
-
|
-
|
-
|
χ2набл=0,16
|
По таблице критических точек распределения χ2кр(α,s)[2] при заданном уровне
значимости α=0,01 и числе степеней свободы s=k-3=4-3=1 находим критическую точку правосторонней критической
области:
χ2кр=
χ2кр(0,01;1)=6,6
Так как χ2набл < χ2кр,
то по данным выборки нет оснований отвергать гипотезу о нормальном
распределении признака X
в генеральной совокупности.
6. Т.к.
генеральная совокупность распределена нормально, то для построения
доверительного интервала генеральной средней можно воспользоваться формулой:
xсрвыб - tγ(s/√n)< xсрген< xсрвыб + tγ(s/√n),
где
s - исправленное выборочное среднее квадратическое
отклонение, равное 0,712 (см. п.5);
tγ находят по таблице[3] по заданным n и γ
γ=0,99 (по условию)
t(0.99, 25)=2,797
tγ(s/√n)=
2,797*0,712/√25=0,4
xсрвыб = 9,06 (см. п.4)
Тогда искомый интервал имеет
вид:
9,06-0,4< xсрген<9,06+0,4
8,66<
xсрген<9,46
Чтобы построить доверительный интервал генеральной дисперсии
сначала найдем доверительный интервал среднего квадратического отклонения по
формуле:
s(1-q) <σген< s(1+q) (при q<1),
0< σген< s(1+q) (при q>1),
где q
находят по таблице[4]
по данным n и γ
q(0.99, 25)=0,49
Доверительный интервал среднего квадратического отклонения:
0,712*(1-0,49) <σген<0,712*(1+0,49)
0,363<σген<1,061
Тогда доверительный интервал генеральной дисперсии имеет
вид:
0,363<Dген<1,061
0,132<Dген<1,125
7. а) Т.к. доверительный интервал генеральной средней 8,66< xсрген<9,46
включает значение
9,2, то с надежностью 0,99 можно утверждать о правильности гипотезы.
б) Т.к. доверительный интервал генеральной дисперсии
0,132<Dген<1,125
не включает
значение 1,653, то с надежностью 0,99 можно отвергнуть гипотезу.
Список использованной литературы
1.
Гмурман В.Е./ Теория вероятностей и математическая
статистика. М.: Высшая школа, 2002
2.
Гмурман В.Е./ Руководство к решению задач по теории
вероятностей и математической статистике. М.: Высшая школа, 2002
3.
Колемаев В.А., Староверов О.В., Турундаевский В.Б./
Теория вероятностей и математическая статистика. М.: Высшая школа, 1991
4.
Семенов А.Т. /Теория вероятностей и математическая
статистика: Учебно-методический комплекс. – Новосибирск: НГАЭиУ, 2003
5.
Семенов А.Т. /Теория вероятностей: Учебное пособие. –
Новосибирск: НГАЭиУ, 2003
[1]
Гмурман В.Е. Руководство к решению задач по теории вероятностей и
математической статистике. М.: Высшая школа, 2002. Прил. 1, С. 388.
[2]
Гмурман В.Е. Руководство к решению задач по теории вероятностей и
математической статистике. М.: Высшая школа, 2002. Прил. 5, С. 393.
[3]
Гмурман В.Е. Руководство к решению задач по теории вероятностей и
математической статистике. М.: Высшая школа, 2002. Прил. 3, С. 392.
[4]
Гмурман В.Е. Руководство к решению задач по теории вероятностей и
математической статистике. М.: Высшая школа, 2002. Прил. 4, С. 392.