ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ ГОУ ВПО
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА СТАТИСТИКИ
КОНТРОЛЬНАЯ РАБОТА
ПО ДИСЦИПЛИНЕ
«СТАТИСТИКА»
ВАРИАНТ № 12
Исполнитель:
Специальность:
финансы и кредит
Группа:
№ зачетной книжки:
Преподаватель:
Голикова А. В.
Москва
2008
ОГЛАВЛЕНИЕ
1. Условие задачи ……………………………………………….. 3
2. Задание 1………………………………………………………. 4
3. Задание 2……………………………………………………….10
4. Задание 3……………………………………………………….19
5. Задание 4……………………………………………………….24
6. Список использованной литературы ………………………...29
Имеются следующие выборочные данные (выборка 25 % -
ная механическая) о доходах[1] и
расходах бюджетов субъектов РФ за полугодие, млн. руб.:
Таблица 1
|
№ региона
п/п
|
Доходы бюджета
|
Расходы
бюджета
|
|
1
|
4,2
|
4,9
|
|
2
|
3,8
|
4,7
|
|
3
|
6,4
|
7,0
|
|
4
|
4,4
|
5,0
|
|
5
|
4,7
|
4,2
|
|
6
|
2,0
|
1,9
|
|
7
|
4,0
|
4,7
|
|
8
|
3,7
|
4,3
|
|
9
|
7,1
|
6,8
|
|
10
|
4,2
|
4,6
|
|
11
|
2,6
|
3,1
|
|
12
|
4,5
|
4,8
|
|
13
|
5,5
|
7,1
|
|
14
|
5,0
|
5,5
|
|
15
|
1,5
|
1,8
|
|
16
|
1,6
|
1,7
|
|
17
|
3,4
|
3,6
|
|
18
|
4,0
|
4,5
|
|
19
|
3,5
|
3,6
|
|
20
|
2,3
|
2,0
|
|
21
|
3,5
|
3,9
|
|
22
|
4,4
|
5,8
|
|
23
|
4,8
|
4,4
|
|
24
|
7,5
|
8,7
|
|
25
|
4,6
|
4,6
|
|
26
|
3,1
|
3,3
|
|
27
|
4,0
|
4,6
|
|
28
|
5,2
|
6,0
|
|
29
|
5,3
|
5,8
|
|
30
|
5,2
|
5,1
|
Задание 1
Признак – доходы бюджета.
Число групп – пять.
РЕШЕНИЕ:
Для выполнения Задания 1 по исходным данным необходимо:
1. Построить статистический ряд распределения регионов
по признаку доходы бюджета, образовав пять групп с равными интервалами;
2. Построить график полученного ряда распределения,
графически определить значение моды и медианы;
3. Рассчитать характеристики интервального ряда
распределения (среднюю арифметическую, среднее квадратическое отклонение,
коэффициент вариации, моду, медиану);
4. Вычислить среднюю арифметическую по исходным
данным, сравнить ее с аналогичным показателем, рассчитанным в пункте 3 для
интервального ряда распределения; объяснить причину их расхождения;
5. Сделать выводы по результатам выполнения задания 1.
ПОСТРОЕНИЕ СТАТИСТИЧЕСКОГО
РЯДА РАСПРЕДЕЛЕНИЯ РЕГИОНОВ ПО ПРИЗНАКУ ДОХОДЫ
БЮДЖЕТА, С ОБРАЗОВАНИЕМ ПЯТИ ГРУПП С РАВНЫМИ ИНТЕРВАЛАМИ.
Сначала необходимо определить длину интервала (шаг
интервала) по формуле: 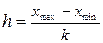 ,
,
где
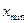 и
и 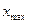 - максимальное и минимальное значения ряда распределения;
- максимальное и минимальное значения ряда распределения;
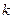 - число групп в группировке (из условия
- число групп в группировке (из условия 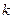 =5).
=5).
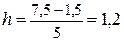 млн.руб.
млн.руб.
При h = 1,2 млн. руб. границы интервалов ряда распределения
имеют следующий вид (табл.2)
Таблица 2
|
Номер группы
|
Нижняя граница
|
Верхняя граница
|
|
1
|
1,5
|
2,7
|
|
2
|
2,7
|
3,9
|
|
3
|
3,9
|
5,1
|
|
4
|
5,1
|
6,3
|
|
5
|
6,3
|
7,5
|
Для построения интервального ряда необходимо
подсчитать число предприятий, входящих в каждую группу (частоты групп). Для этого
будем использовать принцип полуоткрытого интервала [ ), то есть верхние границы
интервалов не принадлежат данным интервалам, а соответствующие им единицы
совокупности включаются не в данную группу, а в следующую.
Таблица 3
|
Группы доходов бюджета
|
Номера регионов
|
Доходы бюджета, млн. руб.
|
|
1,5 – 2,7
|
15
|
1,5
|
|
16
|
1,6
|
|
6
|
2,0
|
|
20
|
2,3
|
|
11
|
2,6
|
|
Всего:
|
5
|
10
|
|
2,7 – 3,9
|
26
|
3,1
|
|
17
|
3,4
|
|
19
|
3,5
|
|
21
|
3,5
|
|
8
|
3,7
|
|
2
|
3,8
|
|
Всего:
|
6
|
21
|
|
3,9 – 5,1
|
7
|
4,0
|
|
18
|
4,0
|
|
27
|
4,0
|
|
1
|
4,2
|
|
10
|
4,2
|
|
4
|
4,4
|
|
22
|
4,4
|
|
12
|
4,5
|
|
25
|
4,6
|
|
5
|
4,7
|
|
23
|
4,8
|
|
14
|
5,0
|
|
Всего:
|
12
|
52,8
|
|
5,1 – 6,3
|
28
|
5,2
|
|
30
|
5,2
|
|
29
|
5,3
|
|
13
|
5,5
|
|
Всего:
|
4
|
21,2
|
|
6,3 – 7,5
|
3
|
6,4
|
|
9
|
7,1
|
|
24
|
7,5
|
|
Всего:
|
3
|
21
|
На основе данных таблицы 3 строим таблицу 4, в которой
отражаем интервальный ряд распределения регионов по доходам бюджета.
Таблица 4
|
Номер группы
|
Группы регионов по доходам бюджета, х
|
Число регионов в группе, f
|
|
1
|
1,5 – 2,7
|
5
|
|
2
|
2,7 – 3,9
|
6
|
|
3
|
3,9 – 5,1
|
12
|
|
4
|
5,1 – 6,3
|
4
|
|
5
|
6,3 – 7,5
|
3
|
|
Всего:
|
30
|
Однако кроме групп в абсолютном выражении в анализе
интервальных рядов также используют частоты
групп в относительном выражении, накопленные (кумулятивные) частоты Sj, значения которых получают путем последовательного
суммирования частот всех предшествующих (j-1) интервалов, и накопленные
частости, рассчитываемые по формуле: 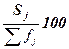 .
.
Структуру регионов по доходам бюджетов представляем в
таблице 5.
Таблица 5
|
Номер группы
|
Группы регионов по доходам бюджета, млн.
руб.
|
Число регионов, 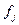
|
Накопленная частота, Sj
|
Накопленная частость, %
|
|
в абсолютном
выражении
|
в % к итогу
|
|
1
|
1,5 – 2,7
|
5
|
16, 7
|
5
|
16,7
|
|
2
|
2,7 – 3,9
|
6
|
20,0
|
11
|
36,7
|
|
3
|
3,9 – 5,1
|
12
|
40,0
|
23
|
76,7
|
|
4
|
5,1 – 6,3
|
4
|
13,3
|
27
|
90
|
|
5
|
6,3 – 7,5
|
3
|
10,0
|
30
|
100,0
|
|
Итого:
|
30
|
100,0
|
|
|
Вывод.
Анализируя интервальный ряд распределения изучаемой
совокупности регионов делаем вывод о том, что распределение регионов по доходам
бюджета не является равномерным. Преобладают регионы с доходами от 3,9
до 5,1 млн. руб. (таких регионов 12, доля их составляет 40%). Пять регионов или 16, 7 % имеют доходы от 1,5
до 2,7 млн. руб., а доходность бюджета от 6,3 до 7,5 млн. руб. зафиксирована
только в 3 регионах (они составляют 10 % от общего числа).
ПОСТРОЕНИЕ
ГРАФИКА РЯДА ПОЛУЧЕННОГО РЯДА РАСПРЕДЕЛЕНИЯ, ГРАФИЧЕСКОЕ И МАТЕМАТИЧЕСКОЕ ОПРЕДЕЛЕНИЯ
ЗНАЧЕНИЙ МОДЫ И МЕДИАНЫ
Мода и медиана - это структурные
средние величины, которые наряду со средней арифметической характеризуют
центр распределения единиц совокупности по изучаемому признаку.
Моду Мо можно определить графическим методом
по гистограмме ряда (рис.1).
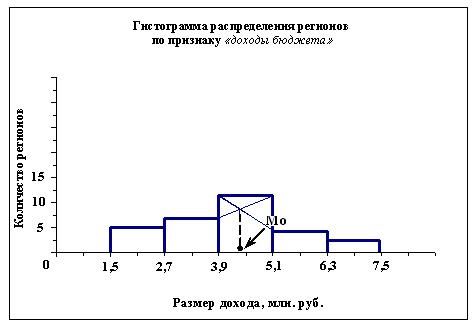
Рис. 1.
Определение моды графическим методом
Конкретное значение моды
для интервального рассчитывают по формуле:
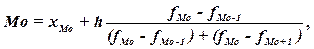
где: хМo –
нижняя граница модального интервала, h –величина модального интервала, fMo
– частота модального интервала, fMo-1 – частота
интервала, предшествующего модальному, fMo+1 –
частота интервала, следующего за модальным.
В нашем случае модальным
интервалом построенного ряда является интервал 3,9 – 5,1 млн. руб., поскольку
частота именно этого интервала составляет 12 регионов и является максимальной.
Рассчитаем моду по
вышеприведенной формуле и получим:
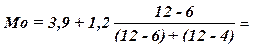 4,41 млн. руб.
4,41 млн. руб.
Вывод.
Для рассматриваемой
совокупности регионов наиболее распространенным доходом в среднем является 4,
41 млн. руб.
Медиану Ме
также можно определить как графическим методом, так и с помощью формулы.
Графическим методом
медиана строиться по кумулятивной кривой (рис. 2). Кумулята строиться по накопленным
частотам.
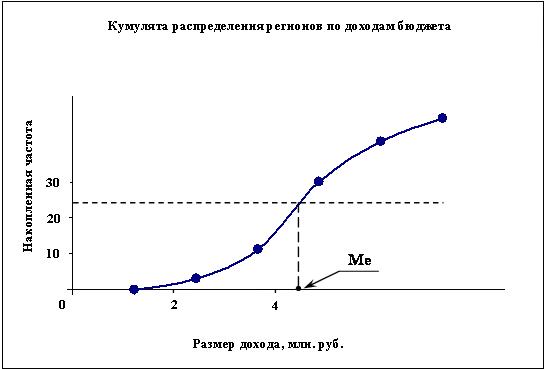
Рис. 2.
Определение медианы графическим методом
Конкретное значение
медианы для интервального ряда рассчитываем по формуле:
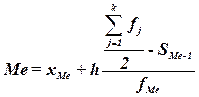 ,
,
где
хМе– нижняя граница медианного интервала,
h – величина медианного интервала,
fМе – частота медианного интервала,
SMе-1 – кумулятивная (накопленная) частота
интервала, предшествующего медианному;
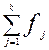 - сумма всех частот.
- сумма всех частот.
Медианный
интервал определим с помощью
использования накопленных частот.
Поскольку Sj = 23 впервые превышает величину,
равную половине численности единиц совокупности (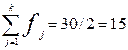 ), поэтому медианным интервалом является интервал 3,9 – 5,1
млн. руб.
), поэтому медианным интервалом является интервал 3,9 – 5,1
млн. руб.
Теперь
рассчитаем значение медианы по вышеприведенной формуле:
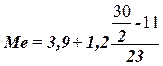 = 4,1 млн.руб.
= 4,1 млн.руб.
Вывод.
В
рассматриваемой совокупности регионов одна половина регионов в среднем имеют
доход не менее 4,1 млн. руб., а другая – не более 4,1 млн. руб.
РАСЧЕТ
ХАРАКТЕРИСТИК ИНТЕРВАЛЬНОГО РЯДА РАСПРЕДЕЛЕНИЯ (СРЕДНЕЙ АРИФМЕТИЧЕСКОЙ ВЗВЕШЕННОЙ,
СРЕДНЕГО КВАДРАТИЧЕСКОГО ОТКЛОНЕНИЯ, КОЭФФИЦИЕНТА ВАРИАЦИИ)
Для расчета характеристик ряда
распределения 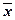 , σ, σ2, Vσ на основе ранее уже известных
значений построим расчетную таблицу для нахождения характеристик ряда
распределения – таблицу 6.
, σ, σ2, Vσ на основе ранее уже известных
значений построим расчетную таблицу для нахождения характеристик ряда
распределения – таблицу 6.
Таблица 6
|
Группы регионов по доходам бюджета
|
Середина интервала,
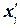
|
Число регионов,
fj
|
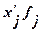
|
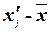
|
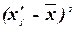
|
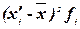
|
|
1,5-2,7
|
2,1
|
5
|
10,5
|
-2,12
|
4,4944
|
22,4720
|
|
2,7-3,9
|
3,3
|
6
|
19,8
|
-0,92
|
0,8464
|
5,0784
|
|
3,9-5,1
|
4,5
|
12
|
54,0
|
0,28
|
0,0784
|
0,9408
|
|
5,1-6,3
|
5,7
|
4
|
22,8
|
1,48
|
2,1904
|
8,7616
|
|
6,3-7,5
|
6,9
|
3
|
20,7
|
2,68
|
7,1824
|
21,5472
|
|
Всего:
|
|
30
|
127,8
|
|
|
58,80
|
Среднюю арифметическую взвешенную
рассчитаем по формуле:
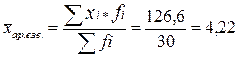 млн.руб.,
млн.руб.,
а по формуле 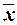 =
= 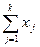 /n = 4,2 млн. руб.
/n = 4,2 млн. руб.
По формуле 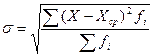 рассчитаем среднее
квадратическое отклонение:
рассчитаем среднее
квадратическое отклонение: 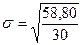 = 1,96
млн.руб.
= 1,96
млн.руб.
Дисперсию рассчитаем по формуле: 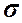 2 = 3, 8416
2 = 3, 8416
Расчет коэффициента вариации проведем
по формуле:
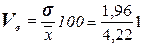 00 = 46,4 %
00 = 46,4 %
Вывод.
Анализируя полученные значения
показателей 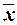 и
и 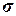 я делаю вывод о том, что средняя величина дохода бюджета
регионов составляет 4,2 млн. руб., отклонение от средней величины в среднем
составляет 1,96 млн. руб. или 46,4 %. Наиболее характерные значения дохода
бюджета региона находятся в пределах от 2,24 до 6,16 млн. руб. (диапазон
я делаю вывод о том, что средняя величина дохода бюджета
регионов составляет 4,2 млн. руб., отклонение от средней величины в среднем
составляет 1,96 млн. руб. или 46,4 %. Наиболее характерные значения дохода
бюджета региона находятся в пределах от 2,24 до 6,16 млн. руб. (диапазон 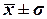 ).
).
Значение Vσ = 46,4 % и превышает 33%, следовательно,
вариация дохода бюджета региона в исследуемой совокупности предприятий значительна,
а совокупность по данному признаку качественно неоднородна. Расхождение между
значениями 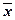 , Мо и Ме незначительно (
, Мо и Ме незначительно (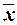 = 4,2 млн. руб., Мо = 4,41 млн. руб., Ме = 4,1 млн. руб.), что подтверждает
вывод об однородности совокупности регионов. Следовательно, найденное среднее
значение дохода бюджета представленных регионов (4,22 млн. руб.) является
типичной, надежной характеристикой исследуемой совокупности регионов.
= 4,2 млн. руб., Мо = 4,41 млн. руб., Ме = 4,1 млн. руб.), что подтверждает
вывод об однородности совокупности регионов. Следовательно, найденное среднее
значение дохода бюджета представленных регионов (4,22 млн. руб.) является
типичной, надежной характеристикой исследуемой совокупности регионов.
Задание 2
Связь между признаками – доходы и расходы
бюджета.
РЕШЕНИЕ:
Для решения данного задания необходимо по исходным
данным установить наличие и характер связи между признаками – доходами и
расходами бюджета – методам аналитической группировки и методом корреляционной
таблицы; измерить между ними тесноту корреляционной связи с использованием
коэффициентов детерминации и эмпирического корреляционного отношения; а также
сделать выводы по результатам выполнения задания.
УСТАНОВЛЕНИЕ НАЛИЧИЯ И ХАРАКТЕРА СВЯЗИ МЕЖДУ
ПРИЗНАКАМИ МЕТОДОМ АНАЛИТИЧЕСКОЙ ГРУППИРОВКИ
Сначала составим вспомогательную таблицу 7 для
построения аналитической группировки.
Таблица 7
|
Номер группы
|
Группы регионов по доходу бюджета,
млн. руб.
|
Номер региона
|
Доход бюджета, млн. руб.
|
Расход бюджета, млн. руб.
|
|
1
|
1,5 – 2,7
|
15
|
1,5
|
1,8
|
|
16
|
1,6
|
1,7
|
|
6
|
2,0
|
1,9
|
|
20
|
2,3
|
2,0
|
|
11
|
2,6
|
3,1
|
|
Всего:
|
5
|
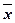 1= 10/5 = 2 1= 10/5 = 2
|
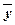 1 = 10,5/5 = 2,1 1 = 10,5/5 = 2,1
|
|
2
|
2,7 – 3,9
|
26
|
3,1
|
3,3
|
|
17
|
3,4
|
3,6
|
|
19
|
3,5
|
3,6
|
|
21
|
3,5
|
3,9
|
|
8
|
3,7
|
4,3
|
|
2
|
3,8
|
4,7
|
|
Всего:
|
6
|
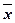 2 = 21/6 = 3,5 2 = 21/6 = 3,5
|
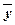 2 = 23,4/6 = 3,9 2 = 23,4/6 = 3,9
|
|
3
|
3,9 – 5,1
|
7
|
4,0
|
4,7
|
|
18
|
4,0
|
4,5
|
|
27
|
4,0
|
4,6
|
|
1
|
4,2
|
4,9
|
|
10
|
4,2
|
4,6
|
|
4
|
4,4
|
5,0
|
|
22
|
4,4
|
5,8
|
|
12
|
4,5
|
4,8
|
|
25
|
4,6
|
4,6
|
|
5
|
4,7
|
4,2
|
|
23
|
4,8
|
4,4
|
|
14
|
5,0
|
5,5
|
|
Всего:
|
12
|
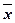 3 = 52,8/12 = 4,4 3 = 52,8/12 = 4,4
|
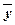 3 = 57,8/12 = 4,8 3 = 57,8/12 = 4,8
|
|
4
|
5,1 – 6,3
|
28
|
5,2
|
6,0
|
|
30
|
5,2
|
5,1
|
|
29
|
5,3
|
5,8
|
|
13
|
5,5
|
7,1
|
|
Всего:
|
4
|
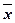 4 = 21,2/4 = 5,3 4 = 21,2/4 = 5,3
|
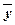 4 = 24/4 = 6 4 = 24/4 = 6
|
|
5
|
6,3 – 7,5
|
3
|
6,4
|
7,0
|
|
9
|
7,1
|
6,8
|
|
24
|
7,5
|
8,7
|
|
Всего:
|
3
|
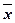 5 = 21/3 = 7 5 = 21/3 = 7
|
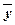 5 = 22,5/3 = 7,5 5 = 22,5/3 = 7,5
|
|
Всего по всем группам:
|
30
|
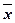 = 4,2 = 4,2
|
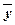 = 4,6 = 4,6
|
Строим аналитическую группировку и представляем ее в таблице
8
Таблица 8
|
Номер группы
|
Доход бюджетов по группам,
млн. руб., хi
|
Средний доход, млн. руб., 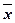 i i
|
Количество регионов, ед., fi
|
Средний расход,
млн. руб., 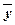 i i
|
|
1
|
1,5 – 2,7
|
2
|
5
|
2,1
|
|
2
|
2,7 – 3,9
|
3,5
|
6
|
3,9
|
|
3
|
3,9 – 5,1
|
4,4
|
12
|
4,8
|
|
4
|
5,1 – 6,3
|
5,3
|
4
|
6
|
|
5
|
6,3 – 7,5
|
7
|
3
|
7,5
|
|
Всего:
|
4,2
|
30
|
4,6
|
Вывод.
Анализируя данные, представленные в таблице 8 можно
сделать вывод о наличии прямой связи между доходом бюджета и его расходом,
поскольку с увеличением дохода увеличивается и расход.
УСТАНОВЛЕНИЕ НАЛИЧИЯ И ХАРАКТЕРА СВЯЗИ МЕЖДУ
ПРИЗНАКАМИ МЕТОДОМ КОРРЕЛЯЦИОННОЙ ТАБЛИЦЫ
Корреляционная таблица представляет собой комбинацию
двух рядов распределения. Строки таблицы соответствуют группировке единиц
совокупности по факторному признаку Х, а графы – группировке по результативному
признаку Y. На пересечении i-ой строки
и k-ой графы укажем число единиц совокупности, которые
входят в i-ый интервал по факторному признаку и в k-ый интервал по признаку результативному.
Построим еще один интервальный ряд распределения, в
котором переменная y
представлена как расход бюджета. Для этого необходимо знать величины и границы интервалов по двум признакам Х и Y. Величину интервала и его границы для факторного признака доход бюджета возьмем их
таблицы 2, также из решения Задания 1 мы знаем, что величина интервала по
признаку доход бюджета составляет 1,2 млн. руб.
Для результативного признака расход бюджета,
представленного Y, величину интервала определим по
формуле 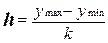 , где k = 5.
, где k = 5.
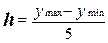 =
= 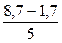 = 7/5 = 1,4 млн. руб.
= 7/5 = 1,4 млн. руб.
Зная шаг интервала по результативному признаку расход
бюджета, определяем границы интервалов ряда распределения
результативного признака Y и отражаем
полученные значения в таблице 9.
Таблица 9
|
Номер группы
|
Нижняя граница, млн. руб.
|
Верхняя граница, млн. руб.
|
|
1
|
1,7
|
3,1
|
|
2
|
3,1
|
4,5
|
|
3
|
4,5
|
5,9
|
|
4
|
5,9
|
7,3
|
|
5
|
7,3
|
8,7
|
Используя принцип полуоткрытого интервала [ ),
подсчитываем количество регионов, входящих в каждую группу (частоты групп) и
получаем интервальный ряд распределения результативного признака, который
отражен в таблице распределения регионов по расходу бюджета, что представлена
ниже.
Таблица 10
Распределение регионов по расходу бюджета
|
Группы регионов по расходу бюджета, млн.
руб. , х
|
Число регионов, fi
|
Номера регионов
|
Расход бюджета,
млн. руб.
|
1,7 – 3,1
|
4
|
16
|
1,7
|
|
15
|
1,8
|
|
6
|
1,9
|
|
20
|
2,0
|
3,1 – 4,5
|
8
|
11
|
3,1
|
|
26
|
3,3
|
|
17
|
3,6
|
|
19
|
3,6
|
|
21
|
3,9
|
|
5
|
4,2
|
|
8
|
4,3
|
|
23
|
4,4
|
4,5 – 5,9
|
13
|
18
|
4,5
|
|
27
|
4,6
|
|
10
|
4,6
|
|
25
|
4,6
|
|
2
|
4,7
|
|
7
|
4,7
|
|
12
|
4,8
|
|
1
|
4,9
|
|
4
|
5,0
|
|
30
|
2,1
|
|
14
|
5,5
|
|
22
|
5,8
|
|
29
|
5,8
|
5,9 – 7,3
|
4
|
28
|
6,0
|
|
9
|
6,8
|
|
3
|
7,0
|
|
13
|
7,1
|
|
7,3 – 8,7
|
1
|
24
|
8,7
|
|
Всего:
|
30
|
|
138
|
Используя группировки по факторному и результативному
признакам, строим корреляционную таблицу.
Таблица 11
Корреляционная таблица зависимости расхода бюджета от
его дохода
|
Группы регионов по доходу бюджета, млн.
руб.
|
Группы регионов по расходу бюджета, млн.
руб.
|
|
1,7-3,1
|
3,1-4,5
|
4,5-5,9
|
5,9-7,3
|
7,3-8,7
|
Всего:
|
|
1,5-2,7
|
4
|
1
|
|
|
|
5
|
|
2,7-3,9
|
|
5
|
1
|
|
|
6
|
|
3,9-5,1
|
|
2
|
10
|
|
|
12
|
|
5,1-6,3
|
|
|
2
|
2
|
|
4
|
|
6,3-7,5
|
|
|
|
2
|
1
|
3
|
|
Всего:
|
4
|
8
|
13
|
4
|
1
|
30
|
Вывод.
Анализ данных таблицы 11 показывает, что распределение
частот групп произошло вдоль диагонали, идущей из левого верхнего угла в правый
нижний угол таблицы. Это свидетельствует о наличии прямой корреляционной связи
между доходам бюджета и его расходом.
ИЗМЕРЕНИЕ ТЕСНОТЫ КОРРЕЛЯЦИОННОЙ СВЯЗИ
МЕЖДУ ПРИЗНАКАМИ
Тесноту корреляционной связи между названными
признаками измерим с использованием коэффициентов детерминации и эмпирического
корреляционного отношения.
Эмпирический
коэффициент детерминации (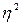 ) определяется как
доля межгрупповой дисперсии в общей дисперсии, характеризует силу влияния
факторного (группировочного) признака на результативный.
) определяется как
доля межгрупповой дисперсии в общей дисперсии, характеризует силу влияния
факторного (группировочного) признака на результативный.
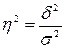
Эмпирическое
корреляционное отношение характеризует
тесноту связи; рассчитывается как корень квадратный из эмпирического
коэффициента детерминации.
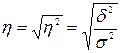
Оба показателя находятся в пределах от 0 до 1.
При этом чем ближе показатели к единице, тем связь
между изучаемыми признаками теснее:
0 – связь отсутствует;
1 –
связь функциональная.
Для оценки тесноты связи с помощью
корреляционного отношения 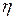 можно воспользоваться
шкалой Чеддока:
можно воспользоваться
шкалой Чеддока:
0,1-0,3 – связь слабая;
0,3-0,5 – связь умеренная;
0,5-0,7 – связь заметная;
0,7-0,9 – связь тесная;
0,9-0,99 – связь весьма тесная.
На основании данных таблицы 7 строим вспомогательную
таблицу для расчета межгрупповой дисперсии
Таблица 12
|
№ гр.
|
Доход бюджета,
млн.руб., 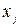
|
Число
регионов, ед.,
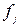
|
Расход бюджета,
млн.руб.
|
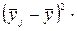 f f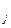
|
|
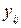
|
в среднем на 1 регион
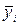
|
|
1
|
1,5-2,7
|
5
|
1,7; 1,8; 1,9; 2,0;
3,1
|
2,1
|
31,25
|
|
2
|
2,7-3,9
|
6
|
3,3; 3,6; 3,6; 3,9;
4,3; 4,7
|
3,9
|
2,94
|
|
3
|
3,9-5,1
|
12
|
4,7; 4,5; 4,6: 4,9;
4,6; 5,0; 5,8; 4,8; 4,6; 4,2; 4,4; 4,5
|
4,8
|
0,48
|
|
4
|
5,1-6,3
|
4
|
6,0; 5,1; 5,8; 7,1
|
6
|
7,84
|
|
5
|
6,3-7,5
|
3
|
7,0; 6,8; 8,7
|
7,5
|
25,23
|
|
Всего:
|
30
|
|
4,6
|
67,74
|
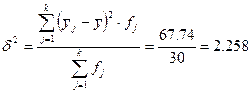
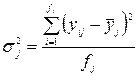 .
.
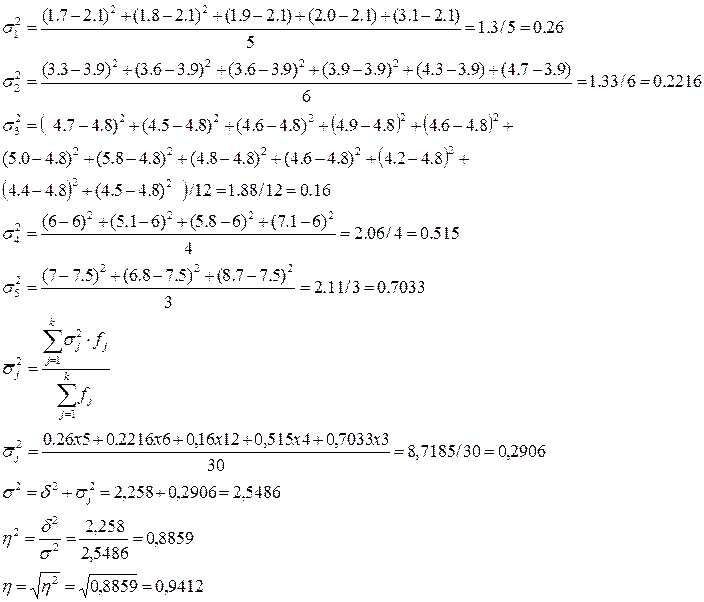
Вывод.
Используя шкалу Чеддока,
можно сделать вывод о том, что связь между доходом бюджета и его расходом
является весьма тесной, так как 0,9412 находится в пределах от 0,9 до 0,99.
Задание 3
По результатам выполнения задания 1 с вероятностью
0,683 определить:
1. Ошибку выборки среднего дохода бюджета и границы, в
которых он будет находиться в генеральной совокупности.
2. Ошибку выборки доли регионов со средним доходом
бюджета 5,1 и более млн. руб. и границы, в которых будет находиться генеральная
доля.
РЕШЕНИЕ:
При выполнении данного задания необходимо определить
ошибку выборки среднего дохода бюджета и долю регионов с уровнем дохода бюджета
не менее 5,1 млн. руб., а также границы, в которых в генеральной совокупности они
будут находиться.
ОПРЕДЕЛЕНИЕ ОШИБКИ ВЫБОРКИ ДЛЯ ВЕЛИЧИНЫ ДОХОДА
БЮДЖЕТА, А ТАКЖЕ ГРАНИЦ, В ПРЕДЕЛАХ КОТОРЫХ БУДЕТ НАХОДИТЬСЯ ГЕНЕРАЛЬНАЯ
СРЕДНЯЯ
Применяя
выборочный метод наблюдения, необходимо рассчитать ошибки выборки (ошибки
репрезентативности), т.к. генеральные и выборочные характеристики, как правило,
не совпадают, а отклоняются на некоторую величину ε.
Принято вычислять два вида
ошибок выборки – среднюю 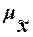 и предельную
и предельную 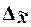 .
.
Для расчета средней ошибки выборки 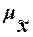 применяются различные формулы в зависимости от вида и способа отбора единиц
из генеральной совокупности в выборочную.
применяются различные формулы в зависимости от вида и способа отбора единиц
из генеральной совокупности в выборочную.
Для собственно-случайной
и механической выборки с бесповторным способом отбора средняя ошибка 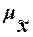 для выборочной средней
для выборочной средней 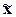 определяется по
формуле:
определяется по
формуле:
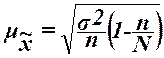 ,
,
где 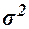 – общая дисперсия изучаемого признака,
– общая дисперсия изучаемого признака,
N – число единиц в генеральной совокупности,
n – число единиц в выборочной совокупности.
Предельная ошибка выборки 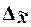 определяет границы, в пределах
которых будет находиться генеральная средняя:
определяет границы, в пределах
которых будет находиться генеральная средняя:
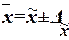 ,
,
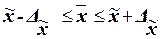 ,
,
где 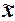 – выборочная средняя,
– выборочная средняя,
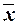 – генеральная средняя.
– генеральная средняя.
Предельная
ошибка выборки 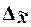 кратна средней ошибке
кратна средней ошибке 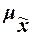 с коэффициентом кратности t (или коэффициент доверия):
с коэффициентом кратности t (или коэффициент доверия):
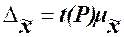
Коэффициент
кратности t зависит от
значения доверительной вероятности
Р, гарантирующей вхождение генеральной средней в интервал 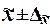 , называемый доверительным интервалом.
, называемый доверительным интервалом.
Наиболее
часто используемые доверительные вероятности Р и соответствующие им
значения t отразим в таблице 13:
Таблица 13
|
Доверительная вероятность P
|
0,683
|
0,866
|
0,954
|
0,988
|
0,997
|
0,999
|
|
Значение t
|
1,0
|
1,5
|
2,0
|
2,5
|
3,0
|
3,5
|
По условию задачи выборочная совокупность насчитывает 30 регионов,
выборка 25% механическая.
Поскольку Р составляет
0,683, то 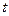 = 1 ,
= 1 ,
В результате решения
задания 2 были определены: дисперсия выборочной совокупности: 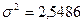 , генеральная средняя:
, генеральная средняя:
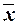 = 4,2 млн. руб.
= 4,2 млн. руб.
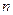 – численность выборки, составляет:
– численность выборки, составляет: 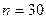 ,
,
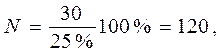
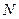 – общее количество регионов, т.к. выборка 25%-ная,
то:
– общее количество регионов, т.к. выборка 25%-ная,
то:
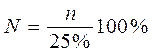
Значения параметров, необходимых для решения задачи,
представим в таблице 14:
Таблица 14
|
Р
|
t
|
n
|
N
|
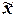
|
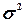
|
|
0,683
|
1
|
30
|
120
|
4,2
|
2,5486
|
Следовательно,
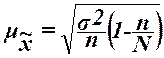 =
= 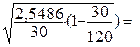
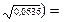 0,2522 млн. руб.
0,2522 млн. руб.
Определяем предельную
выборку:
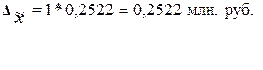
и
доверительный интервал для генеральной средней:
4,2 -0,2522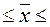 4,2 +0,2522
4,2 +0,2522
3,9478 млн. руб. 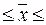 4,4522 млн. руб.
4,4522 млн. руб.
Вывод.
На основании проведенного выборочного обследования региональных бюджетов с
вероятностью 0,683 можно утверждать, что для генеральной совокупности регионов
величина среднего дохода бюджета находится в пределах от 3, 9478 млн. руб. до 4, 4522 млн. руб.
ОПРЕДЕЛЕНИЕ ОШИБКИ ВЫБОРКИ ДОЛИ РЕГИОНОВ СО СРЕДНИМ ДОХОДОМ БЮДЖЕТА 5,1
МЛН. РУБ. И ГРАНИЦ, В КОТОРЫХ БУДЕТ НАХОДИТЬСЯ ГЕНЕРАЛЬНАЯ ДОЛЯ.
Доля
единиц выборочной совокупности, обладающих тем или иным заданным свойством,
выражается формулой:
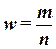 ,
,
где
m – число
единиц совокупности, обладающих заданным свойством;
n – общее число единиц в совокупности.
Для
собственно-случайной и механической выборки с бесповторным способом отбора предельная ошибка выборки 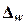 доли единиц,
обладающих заданным свойством, рассчитывается по формуле:
доли единиц,
обладающих заданным свойством, рассчитывается по формуле:
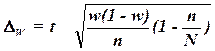 ,
,
где
w – доля
единиц совокупности, обладающих заданным свойством;
(1-w) – доля единиц совокупности, не
обладающих заданным свойством,
N – число единиц в генеральной
совокупности,
n– число единиц в выборочной
совокупности.
Определим долю регионов с
доходом бюджета 5,1 и более млн. руб. в выборке; она равна отношению количеству
регионов с указанной величиной дохода бюджета (7 шт.) ко всему количеству предприятий
в выборке (30 шт.):
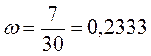
Определим предельную
ошибку выборки для доли (выборка 25%-ная механическая):
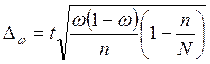 ,
,
где 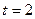 , так как Р = 0, 683,
, так как Р = 0, 683, 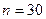 регионов, а
регионов, а 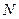 = 120 регионов.
= 120 регионов.
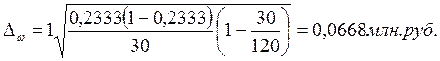
Границы, в которых будет
находиться генеральная доля:
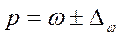 ,
,
следовательно: 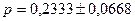 ;
; 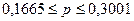
или 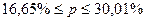
Вывод. С вероятностью 0,683 можно утверждать, что в
генеральной совокупности регионов доля регионов с доходом бюджета 5,1 млн. руб и
выше будет находиться в пределах от 16,65 % до 30,01 %.
Задание 4
Налоговые поступления в региональный бюджет
характеризуются следующими данными, млн. руб.:
Таблица 15
|
Год
Месяц
|
Налоговые поступления
|
|
1-й
|
2-й
|
3-й
|
|
Январь
|
0,62
|
0,72
|
0,74
|
|
Февраль
|
0,65
|
0,75
|
0,77
|
|
Март
|
0,70
|
0,76
|
0,78
|
|
Апрель
|
0,72
|
0,77
|
0,82
|
|
Май
|
0,74
|
0,80
|
0,84
|
|
Июнь
|
0,76
|
0,82
|
0,85
|
|
Июль
|
0,71
|
0,78
|
0,80
|
|
Август
|
0,70
|
0,75
|
0,78
|
|
Сентябрь
|
0,82
|
0,88
|
0,90
|
|
Октябрь
|
0,85
|
0,89
|
0,96
|
|
Ноябрь
|
0,88
|
0,94
|
0,99
|
|
Декабрь
|
0,90
|
0,98
|
1,05
|
Для
анализа сезонности налоговых поступлений в бюджет региона:
-
рассчитать индексы сезонности методом простой средней;
-
построить график сезонной волны;
-
осуществить прогноз поступления налогов в бюджет региона по месяцам, используя
индексы сезонности и исходя из того, что общий объем налоговых поступлений в
следующем (4-м) году составит 11, 4 млн. руб.
РЕШЕНИЕ:
Индекс
сезонности считаем по формуле: 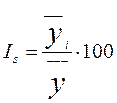 ,
,
где:
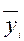 - средняя для каждого месяца за три года;
- средняя для каждого месяца за три года;
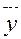 -среднемесячный уровень для всего ряда.
-среднемесячный уровень для всего ряда.
Для
упрощения расчетов при выполнении здания построим расчетную таблицу 16:
Таблица 16
|
Месяц
|
1-ый год
|
2-ой год
|
3-ий год
|
Среднемесячная
|
Is
|
|
Январь
|
0,62
|
0,72
|
0,74
|
0,693333
|
85, 5674
|
|
Февраль
|
0,65
|
0,75
|
0,77
|
0,723333
|
89, 269842
|
|
Март
|
0,70
|
0,76
|
0,78
|
0,746666
|
92, 149474
|
|
Апрель
|
0,72
|
0,77
|
0,82
|
0,77
|
95, 02923
|
|
Май
|
0,74
|
0,80
|
0,84
|
0,793333
|
97, 908863
|
|
Июнь
|
0,76
|
0,82
|
0,85
|
0,81
|
99, 965814
|
|
Июль
|
0,71
|
0,78
|
0,80
|
0,763333
|
94, 206425
|
|
Август
|
0,70
|
0,75
|
0,78
|
0,743333
|
91, 783133
|
|
Сентябрь
|
0,82
|
0,88
|
0,90
|
0,866666
|
106, 959225
|
|
Октябрь
|
0,85
|
0,89
|
0,96
|
0,9
|
111, 073126
|
|
Ноябрь
|
0,88
|
0,94
|
0,99
|
0,936666
|
115, 598246
|
|
Декабрь
|
0,90
|
0,98
|
1,05
|
0,976666
|
120, 534829
|
|
Всего:
|
|
|
|
9,723329
|
1200, 045607
|
|
В среднем:
|
|
|
|
0,810277
|
100, 0038
|
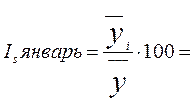
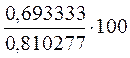 = 85, 5674
= 85, 5674
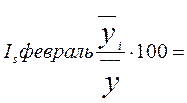
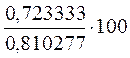 = 89, 269842
= 89, 269842
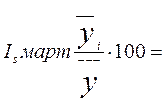
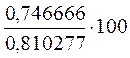 = 92, 149474
= 92, 149474
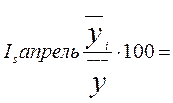
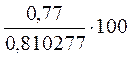 = 95, 02923
= 95, 02923
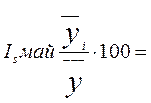
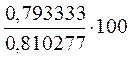 = 97, 908863
= 97, 908863
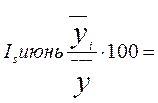
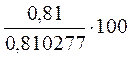 = 99, 965814
= 99, 965814
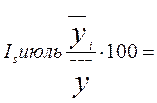
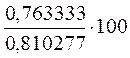 = 94, 206425
= 94, 206425
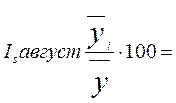
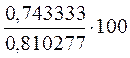 = 91, 738133
= 91, 738133
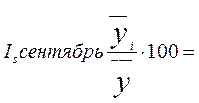
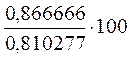 = 106, 959225
= 106, 959225
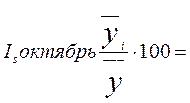
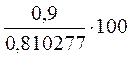 = 111, 073126
= 111, 073126
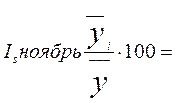
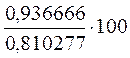 = 115, 598246
= 115, 598246
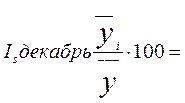
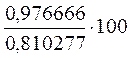 = 120, 534829
= 120, 534829
Отобразим
сезонные поступления налогов в бюджет региона графически:
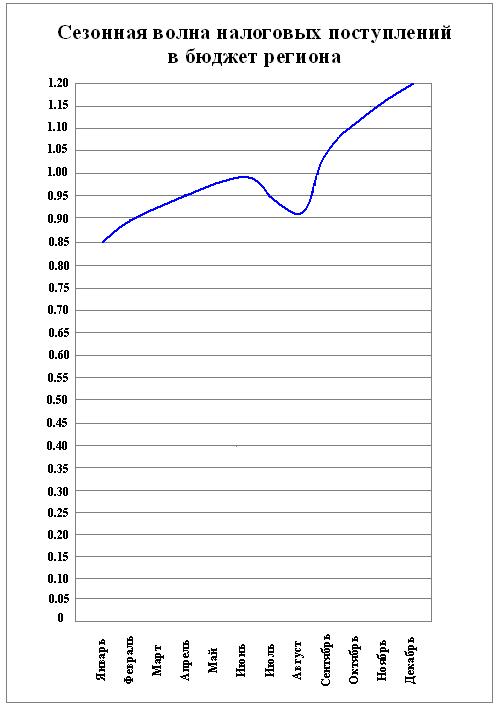
Для
осуществления прогноза поступления налогов в бюджет региона по месяцам,
используя индексы сезонности и исходя из того, что общий объем налоговых
поступлений в следующем (4-м) году составит 11, 4 млн. руб. необходимо найти
среднее значение объема налоговых поступлений по 12 месяцам:
11,
4 млн. руб./12 мес. = 0,95 млн. руб.
Для
определения прогноза поступления налогов в бюджет региона по месяцам построим
таблицу 17 и спрогнозируем объем налоговых поступлений путем умножения средней
величины на сезонный индекс:
Таблица 17
|
Месяц
|
Is
|
Прогноз
|
|
Январь
|
0,855674
|
0,8128903
|
|
Февраль
|
0,89269842
|
0,848063499
|
|
Март
|
0,92149474
|
0,875420003
|
|
Апрель
|
0,9502923
|
0,902777685
|
|
Май
|
0,97908863
|
0,9301341985
|
|
Июнь
|
0,99965814
|
0,949675233
|
|
Июль
|
0,94206425
|
0,8949610375
|
|
Август
|
0,91783133
|
0,8719397635
|
|
Сентябрь
|
1,06959225
|
1,0161126375
|
|
Октябрь
|
1,11073126
|
1,055194697
|
|
Ноябрь
|
1,15598246
|
1,098183337
|
|
Декабрь
|
1,20534829
|
1,1450808755
|
|
Всего:
|
12,
00045607
|
11,4004332665
|
|
В среднем:
|
1, 000038
|
0,95003610554
|
Список
использованной литературы
1.
Громыко Г.Л. Теория статистики: Учебник. - М.:
ИНФРА-М, 2006.
2.
Громыко Г.Л. Теория статистики: Практикум. - М.:
ИНФРА-М, 2003.
3.
Гусаров
В.М. Статистика: Учеб пособие/ В.М. Гусаров, Е.И. Кузнецова. – 2-е изд.,
перераб. и доп. – М.: ЮНИТИ-ДАНА, 2007.
4.
Ефимов
М.Р., Петрова Е.В., Румянцев В.Н., Общая теория статистики: Учебник. – М.:
ИНФРА – М, 2004
5. Общая теория статистики:
Статистическая методология в изучении коммерческой деятельности: Учебник / Под.
ред. Башиной О.Э., Спирина А.А. – М.: Финансы и статисика, 2005.
6.
Практикум
по статистике: Учебное пособие / Под ред. В.М. Симчеры- М.: Финстатинформ, 1999 г.
7.
Статистика
финансов: Учебник/ Под редакцией М.Г. Назарова-М.: Омега-Л , 2005 г. ,с.168.
8. Теория статистики: Учебник/Под. ред.
Шмойловой Р.А. – М.: Финансы и статистика, 2001; 2003; 2006.
[1] Доходы включают в себя
поступления от налога на прибыль организаций, налога на физических лиц,
акцизов; налогов на имущество, платежей за пользование природными ресурсами.