ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КОНТРОЛЬНАЯ РАБОТА
студента
3 курса
по
дисциплине «Эконометрика»
Вариант № 22
Задание
I.
|
Номер
|
Номер
наблюдения, t
|
|
показателя
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
42:
Y(t)
|
65
|
67
|
63
|
60
|
56
|
63
|
57
|
53
|
51
|
Требуется:
1) определить
наличие тренда Y(t);
2) построить
линейную модель Y(t) = a0 + a1 * t, параметры которой
оценить с помощью МНК;
3) оценить
адекватность построенных моделей на основе исследования:
а) случайности остаточной компоненты
по критерию пиков;
б) независимости уровней ряда
остатков по d-критерию (в качестве критических использовать уровни d1
= 1,08 и d2 = 1,36 ) или по первому коэффициенту корреляции,
критический уровень которого r(1) = 0,36;
в) нормальности распределения
остаточной компоненты по R/S-критерию с критическими уровнями 2,7 – 3,7;
4) для оценки
точности использовать среднеквадратическое отклонение и среднюю по модулю
относительную ошибку;
5) построить
точечный и интервальный прогнозы на два шага вперед (для вероятности
Р = 70% использовать коэффициент t a,n
= 1,11).
Решение:
1) Наличие тренда
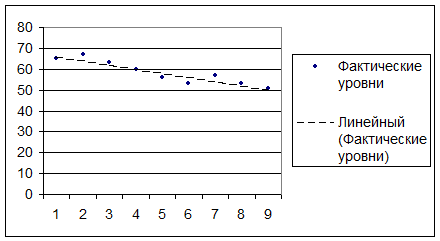
Визуальный анализ графика динамики ряда показывает
наличие убывающей тенденции (пунктир). Вывод: возможно существование линейного
тренда (тенденции среднего текущего значения).
Для проверки
этого предположения воспользуемся методом Фостера-Стьюарта:
а) построим
ряды дополнительных переменных сравнения
Ut
= 1, если текущее значение Yt больше всех предыдущих членов ряда;
иначе Ut = 0
Lt
= 1, если текущее значение Yt меньше всех предыдущих членов ряда;
иначе Lt = 0
а также: St = Ut + Lt
и Dt
= Ut - Lt
|
t
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
|
Yt
|
65
|
67
|
63
|
60
|
56
|
53
|
57
|
53
|
51
|
сумма
|
|
Ut
|
—
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
уровней
|
|
Lt
|
—
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
S,
D
|
|
St
|
—
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
6
|
|
Dt
|
—
|
1
|
-1
|
-1
|
-1
|
-1
|
0
|
0
|
-1
|
-4
|
б) вычислим
значения t-статистик Стьюдента для величин S и D
t S = | S - m | / s1
t
D = | D | / s2
где m
, s1
и s2
– табличные значения для соответственно математического ожидания величины S и
среднеквадратических отклонений для величин S и D.
Принимая m =
3,858; s1
= 1,288 и s2
= 1,964 (из курса лекций) получим t S = 1,663 и
t D = 2,037
в) сравним полученные
значения с табличным значением t-критерия Стьюдента
Принимая табличное
значение критерия Стьюдента t (1-a)=0,9 k=8 = 1,8595
получим
t D
= 2,037 >1,8595 - тренд есть;
t S = 1,663 < 1,8595 -
тенденция в дисперсии отсутствует (т.е. дисперсия остатков гомоскедастична,
следовательно, выполняется предпосылка для использования традиционного метода
наименьших квадратов).
2) Линейная модель тренда
Так как модель Y(t) = a0
+ a1 * t линейна относительно параметров a0 и a1
, то для их оценки применим метод наименьших квадратов (традиционный):
a0
= yср – a1
* tср
a1
= ånt=1 ( Yt - yср ) * ( t - tср ) / ånt=1 ( t - tср ) 2
yср = ( ånt=1 Yt ) / n
tср = ( ånt=1 t ) / n
где: yср, tср – средние
значения;
Yt, t – текущие значения;
n – длина (количество уровней) ряда.
ånt=1
– операция суммирования значений уровней с номером t в диапазоне от 1 до n.
Результаты
промежуточных расчетов приведены в таблице 1.
Таблица 1
|
t
|
Yt
|
t
- tср
|
(
t
– tср )2
|
Yt
-Yср
|
(t
- tср)*( Yt -Yср)
|
|
1
|
65
|
-4
|
16
|
6.67
|
-26.67
|
|
2
|
67
|
-3
|
9
|
8.67
|
-26.00
|
|
3
|
63
|
-2
|
4
|
4.67
|
-9.33
|
|
4
|
60
|
-1
|
1
|
1.67
|
-1.67
|
|
5
|
56
|
0
|
0
|
-2.33
|
0.00
|
|
6
|
53
|
1
|
1
|
-5.33
|
-5.33
|
|
7
|
57
|
2
|
4
|
-1.33
|
-2.67
|
|
8
|
53
|
3
|
9
|
-5.33
|
-16.00
|
|
9
|
51
|
4
|
16
|
-7.33
|
-29.33
|
|
5
|
58.33
|
|
60
|
|
-117.00
|
|
tср
|
Yср
|
|
сумма
|
|
сумма
|
Тогда
a1
= -117 / 60 = -1,95 a0
= 58,33 – (-1,95) * 5 = 68,08
Таким
образом, искомая линейная модель имеет вид:
<Y(t)>
= 68,08 – 1,95 * t
где:
<Y(t)> - расчетное значение признака Y.
3) Оценка
адекватности построенной модели.
Для оценки адекватности построенной
модели исследуем ряд остатков отклонений расчетных значений <Y(t)> от
фактических Yt (здесь и далее расчеты сведены в
таблицу 2):
et = Yt – <Y(t)>
Таблица 2
|
t
|
Y(t)
|
<Y(t)>
|
et
|
точка
поворота
|
et
2
|
et
- et-1
|
( et
- et-1
) 2
|
|
1
|
65
|
66.13
|
-1.13
|
-
|
1.28
|
-
|
-
|
|
2
|
67
|
64.18
|
2.82
|
1
|
7.93
|
3.95
|
15.60
|
|
3
|
63
|
62.23
|
0.77
|
0
|
0.59
|
-2.05
|
4.20
|
|
4
|
60
|
60.28
|
-0.28
|
0
|
0.08
|
-1.05
|
1.10
|
|
5
|
56
|
58.33
|
-2.33
|
0
|
5.44
|
-2.05
|
4.20
|
|
6
|
53
|
56.38
|
-3.38
|
1
|
11.45
|
-1.05
|
1.10
|
|
7
|
57
|
54.43
|
2.57
|
1
|
6.59
|
5.95
|
35.40
|
|
8
|
53
|
52.48
|
0.52
|
0
|
0.27
|
-2.05
|
4.20
|
|
9
|
51
|
50.53
|
0.47
|
-
|
0.22
|
-0.05
|
0.00
|
|
|
|
0.00
|
3
|
33.85
|
|
65.82
|
|
|
|
eср
|
всего
|
сумма
|
|
сумма
|
а) случайность
остаточной компоненты по критерию пиков
Определим количество поворотных точек (т.е. таких точек,
значение уровня в которой одновременно больше соседних с ним или, наоборот,
одновременно меньше предыдущего и последующего за ним уровня).
Обозначения: 1 – точка поворота; 0 –
в противном случае.
Критическое число поворотных точек
определяется по формуле:
ркр
= 2/3 * ( n – 2) – 1,96 * SQR[(16 * n – 29) / 90],
где: SQR[ ] –
операция извлечение квадратного корня.
Подставив значение n = 9, получим ркр
= 2,4511. Так как суммарное количество поворотных точек больше критического значения,
то гипотеза о случайности остаточной
компоненты принимается.
б) независимость уровней ряда остатков друг от друга по d-критерию
Значение d-критерия Дарбина-Уотсона
(на отсутствие автокорреляции между уровнями или, другими словами, зависимости
последующих значений от предыдущих) определяется по формуле:
d = ånt=2 ( et
- et-1
) 2 / ånt=1 et 2
Из таблицы 2:
d = 65,82 / 33,85 = 1,94
Вычисленное
значение d = 1,94 попадает в интервал d2 = 1,36 < d < 2,
следовательно, гипотеза о независимости
уровней ряда остатков друг от друга принимается.
Так как с помощью d-критерия
Дарбина-Уотсона получено вполне определенно суждение, то нет необходимости в
применении дополнительного критерия адекватности модели по первому коэффициенту
корреляции.
в) нормальность распределения остаточной компоненты по R/S-критерию
Значение R/S-критерия определяется
по формуле:
R/S = ( emax – emin ) / Se
Se = SQR[ ånt=1 ( et - eср ) 2 / ( n – 1 ) ]
eср = ( ånt=1
et
) / n
где: emax
и emin
– максимальный и минимальный уровни ряда остатков;
eср – среднее значение ряда остатков;
Se - среднеквадратическое отклонение;
n – длина (количество уровней) ряда.
Значения из таблицы 2: emax = 2,82 emin = -3,38
Так как eср
= 0, то ånt=1
( et
- eср
) 2 = ånt=1 et 2
= 33,85
Тогда
R/S = (2,82 – (-3,38)) / SQR[ 33,85 / (9-1)] = 3,014
Так как значение R/S-критерия
попадает в интервал между критическими уровнями 2,7 и 3,7 – то гипотеза о нормальном распределении ряда
остатков принимается.
Общие выводы: поскольку все три
критерия выполняются, а также среднее значение ряда остатков равно нулю
(следовательно, расчетное значение t-критерия Стьюдента
t расч = | eср | * SQR[ n ] / Se = 0 ,
т.е.
критерий Стьюдента tрасч < tтабл выполняется), то
– линейная трендовая модель является адекватной фактическому ряду динамики;
– модель может быть использована для построения прогнозных оценок.
4) Оценка
точности модели.
Стандартная ошибка оценки (или среднеквадратическое
отклонение от линии тренда) определяется по формуле
S<Y(t)>
= SQR[ ånt=1 ( Yt - <Y(t)> )
2 / ( n – m ) ]
где: m – число параметров модели ( в данном случае m=2 ).
Так как et
= Yt
– <Y(t)>, то из таблицы 2 видно, что ånt=1
( Yt - <Y(t)> ) 2 = 33,85
Тогда
S<Y(t)>
= SQR[33,85 / ( 9 – 2 )] = 2,199
Средняя
относительная ошибка аппроксимации (по модулю) определяется по формуле
Еотн = ( ånt=1
| et
/ Yt | ) / n * 100%
Промежуточные расчетные
данные приведены в таблице 3.
Таблица 3
|
t
|
Yt
|
<Y(t)>
|
et
|
et
/ Yt
|
| et
/ Yt |
|
|
1
|
65
|
66,13
|
-1,13
|
-0,017
|
0,017
|
|
2
|
67
|
64,18
|
2,82
|
0,042
|
0,042
|
|
3
|
63
|
62,23
|
0,77
|
0,012
|
0,012
|
|
4
|
60
|
60,28
|
-0,28
|
-0,005
|
0,005
|
|
5
|
56
|
58,33
|
-0,33
|
-0,042
|
0,042
|
|
6
|
53
|
56,38
|
-3,38
|
-0,064
|
0,064
|
|
7
|
57
|
54,43
|
2,57
|
0,045
|
0,045
|
|
8
|
53
|
52,48
|
0,52
|
0,01
|
0,01
|
|
9
|
51
|
50,53
|
0,47
|
0,009
|
0,009
|
|
|
|
|
|
0,246
|
|
|
|
|
|
сумма
|
Окончательно: Еотн = 0,246 / 9 * 100% =
2,73%
Так как Еотн <
5%, то модель считается точной.
5)
Точечный и интервальный прогнозы.
Для периода упреждения на k = 2 шага вперед значение tпрогноз
= n + k = 9 + 2 = 11. Подставив полученное значение t в линейную модель,
получим точечный прогноз
<Y(t=11)>
= 68,08 – 1,95 * 11 = 46,63
Интервальный прогноз
рассчитывается с помощью доверительных интервалов по формуле
<Y(tпрогноз)> ± t a,n
* Sпрогноз
где для линейной
модели
Sпрогноз= S<Y(t)> * SQR[ (1 +
1 / n + (n+k- tср)2) / ånt=1
( t - tср ) 2]
В таблице 1 рассчитано tср
=5 и ånt=1
( t - tср ) 2 = 60, а из предыдущего раздела S<Y(t)>
= 2,199.
Тогда
Sпрогноз= 2,199 * SQR[ (1 + 1 / 9 + (9+2-5)2)
/ 60 ] = 1,7294 »
1,73
Так как по условию ta,n
= 1,11 интервальный прогноз на 2 шага
вперед имеет следующий вид:
46,63
±
1,92 (при уровне доверительной вероятности P = 0,7)
Задание
II.
|
Номер
|
Номер
наблюдения, t
|
|
показателя
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
42:
Y(t)
|
65
|
67
|
63
|
60
|
56
|
53
|
57
|
53
|
51
|
|
43:
X1(t)
|
29
|
33
|
32
|
36
|
38
|
41
|
44
|
42
|
46
|
|
44:
X2(t)
|
35
|
40
|
44
|
50
|
53
|
57
|
56
|
60
|
62
|
Требуется:
1) построить матрицу коэффициентов парной корреляции Y(t) с X1(t)
и X2(t) и выбрать фактор, наиболее тесно связанный с зависимой
переменной Y(t);
2)
построить линейную однопараметрическую модель регрессии Y(t) = a0 +
a1 * Х(t);
3)
оценить качество построенной модели, исследовав ее адекватность и точность;
4) для
модели регрессии рассчитать коэффициент эластичности и b-коэффициент;
5) построить точечный и
интервальный прогнозы на два шага вперед по модели регрессии (для вероятности Р
= 70% использовать коэффициент n = 1,11). Прогнозные оценки фактора X(t) на два шага
вперед получить на основе среднего прироста от фактически достигнутого уровня).
Решение:
1)
Матрица коэффициентов парной корреляции.
Выборочный парный линейный коэффициент корреляции
рассчитывается по формуле
ry,x = ånt=1
( Yt - yср ) * (Xt - xср ) / SQR[ ånt=1
( Yt - yср ) 2 * ånt=1
(Xt - xср ) 2 ]
Промежуточные
результаты расчетов для коэффициента ry,x1 приведены в таблице 4
Таблица
4
|
t
|
Y(t)
|
X1(t)
|
Y(t) - yср
|
X1(t) - x1cр
|
(Yt - yср)2
|
(X1t - x1cр) 2
|
(Y(t) - yср)*( X1t - x1cр)
|
|
1
|
65
|
29
|
6,67
|
-8,89
|
44,44
|
79,01
|
-59,23
|
|
2
|
67
|
33
|
8,67
|
-4,89
|
75,11
|
23,90
|
-42,31
|
|
3
|
63
|
32
|
4,67
|
-5,89
|
21,78
|
34,68
|
-27,46
|
|
4
|
60
|
36
|
1,67
|
-1,89
|
2,78
|
3,57
|
-3,14
|
|
5
|
56
|
38
|
-2,33
|
0,11
|
5,44
|
0,01
|
-0,28
|
|
6
|
53
|
41
|
-5,33
|
3,11
|
28,44
|
9,68
|
-16,63
|
|
7
|
57
|
44
|
-1,33
|
6,11
|
1,78
|
37,35
|
-8,14
|
|
8
|
53
|
42
|
-5,33
|
4,11
|
28,44
|
16,90
|
-21,96
|
|
9
|
51
|
46
|
-7,33
|
8,11
|
53,78
|
65,79
|
-59,52
|
|
58,33
|
37,89
|
|
|
262,00
|
270,89
|
-238,67
|
|
yср
|
x1cр
|
|
|
сумма
|
сумма
|
сумма
|
Тогда
ry,x1 = -238,67 / SQR[ 262,00 *270,89] =
-238,67 / 266,41= -0,9
Промежуточные результаты
расчетов для коэффициента ry,x2 приведены в таблице 5
Таблица
5
|
t
|
Y(t)
|
X2(t)
|
Y(t) - yср
|
X2(t) – x2cр
|
(Yt - yср)2
|
(X2t - x2cр) 2
|
(Y(t) - yср)*( X2t - x2cр)
|
|
1
|
65
|
35
|
6,67
|
-15,78
|
44,44
|
248,94
|
-105,2
|
|
2
|
67
|
40
|
8,67
|
-10,78
|
75,11
|
116,16
|
-93,41
|
|
3
|
63
|
44
|
4,67
|
-6,78
|
21,78
|
45,94
|
-31,63
|
|
4
|
60
|
50
|
1,67
|
-0,78
|
2,78
|
0,60
|
-1,296
|
|
5
|
56
|
53
|
-2,33
|
2,22
|
5,44
|
4,94
|
-5,185
|
|
6
|
53
|
57
|
-5,33
|
6,22
|
28,44
|
38,72
|
-33,19
|
|
7
|
57
|
56
|
-1,33
|
5,22
|
1,78
|
27,27
|
-6,963
|
|
8
|
53
|
60
|
-5,33
|
9,22
|
28,44
|
85,05
|
-49,19
|
|
9
|
51
|
62
|
-7,33
|
11,22
|
53,78
|
125,94
|
-82,3
|
|
58,33
|
50,78
|
|
|
262,00
|
693,56
|
-408,33
|
|
yср
|
x2cр
|
|
|
сумма
|
сумма
|
сумма
|
Тогда
ry,x2 = -408,33 / SQR[ 262,00 * 693,56 ] =
-408,33 / 426,28 = -0,96
Для построения полной матрицы коэффициентов
парной корреляции необходимо вычислить коэффициент rx1,x2 (таблица
6)
Таблица 6
|
t
|
X1(t)
|
X2(t)
|
X1(t) – x1cр
|
X2(t) – x2cр
|
(X1t - x1cр) 2
|
(X2t - x2cр) 2
|
(X1t - x1cр)*(X2t - x2cр)
|
|
1
|
29
|
15
|
-8,89
|
-15,78
|
79,01
|
248,94
|
140,13
|
|
2
|
33
|
20
|
-4,89
|
-10,78
|
23,90
|
116,16
|
52,61
|
|
3
|
32
|
24
|
-5,89
|
-6,78
|
34,68
|
45,94
|
39,87
|
|
4
|
36
|
30
|
-1,89
|
-0,78
|
3,57
|
0,60
|
1,466
|
|
5
|
38
|
33
|
0,11
|
2,22
|
0,01
|
4,94
|
0,266
|
|
6
|
41
|
37
|
3,11
|
6,22
|
9,68
|
38,72
|
19,416
|
|
7
|
44
|
36
|
6,11
|
5,22
|
37,35
|
27,27
|
31,95
|
|
8
|
42
|
40
|
4,11
|
9,22
|
16,90
|
85,05
|
37,99
|
|
9
|
46
|
42
|
8,11
|
11,22
|
65,79
|
125,94
|
91,11
|
|
37,89
|
50,78
|
|
|
270,89
|
693,56
|
414,80
|
|
x1cр
|
x2cр
|
|
|
сумма
|
сумма
|
сумма
|
Тогда
rx1,x2 = 414,78 / SQR[270,89* 693,56 ] = 414,78
/433,45 =0,9569 »
0,96
И матрица коэффициентов
парной корреляции, построенная по вычисленным значениям, имеет вид:
|
1
|
ry,x1
= -0,9
|
ry,x2
= -0,96
|
|
rx1,y
= -0,9
|
1
|
rx1,x2
= 0,96
|
|
rx2,y
= -0,96
|
rx2,x1
= 0,96
|
1
|
Вывод: среди двух факторов X1(t) и X2(t) наиболее тесно связанным с
зависимой переменной Y(t) является фактор X1(t), так как в абсолютном выражении коэффициент ry,x1
наиболее близок к 1. Отрицательное значение коэффициента корреляции означает
обратную (разнонаправленную) линейную связь между Y(t) и X1(t).
2) Линейная однопараметрическая (однофакторная) модель регрессии.
Так как модель Y(t) = a0
+ a1 * X(t) линейна относительно параметров a0 и a1
, то для их оценки применим метод наименьших квадратов (традиционный):
a0
= yср – a1
* xср
a1
= ånt=1 ( Yt - yср ) * ( Xt - xср ) / ånt=1 (Xt - xср ) 2
yср = ( ånt=1 Yt ) / n
xср = ( ånt=1 Xt ) / n
где: yср, xср – средние
значения переменных;
Yt, Xt –
текущие значения переменных в момент наблюдения t;
n – длина (количество уровней) ряда
наблюдений;
ånt=1
– операция суммирования значений уровней с номером t в диапазоне от 1 до n.
Промежуточные результаты расчетов для зависимой переменной Y(t) и фактора
X1(t), приведены в
таблице 7
Таблица 7
|
t
|
Y(t)
|
Yt
- yср
|
X1(t)
|
X1t
- x1ср
|
(Yt
- yср)*(X1t
- x1ср)
|
(X1t
- x1ср) 2
|
|
1
|
65
|
6,67
|
29
|
-8,89
|
-59,23
|
79,01
|
|
2
|
67
|
8,67
|
33
|
-4,89
|
-42,31
|
23,90
|
|
3
|
63
|
4,67
|
32
|
-5,89
|
-27,46
|
34,68
|
|
4
|
60
|
1,67
|
36
|
-1,89
|
-3,14
|
3,57
|
|
5
|
56
|
-2,33
|
38
|
0,11
|
-0,28
|
0,01
|
|
6
|
53
|
-5,33
|
41
|
3,11
|
-16,63
|
9,68
|
|
7
|
57
|
-1,33
|
44
|
6,11
|
-8,14
|
37,35
|
|
8
|
53
|
-5,33
|
42
|
4,11
|
-21,96
|
16,90
|
|
9
|
51
|
-7,33
|
46
|
8,11
|
-59,52
|
65,79
|
|
58,33
|
|
37,89
|
|
-238,67
|
270,89
|
|
yср
|
|
x1ср
|
|
сумма
|
сумма
|
Тогда
a1
= -238,67 / 270,89= -0,88 a0
= 58,33 – (-0,881) * 37,89 = 91,72
Таким
образом, искомая линейная модель имеет вид:
<Y(t)>
=91,72– 0,881 * X1(t)
где:
<Y(t)> - расчетное значение зависимой переменной Y.
3) Оценка адекватности и точности линейной однофакторной модели
регрессии.
Для оценки адекватности и точности линейной однофакторной
модели регрессии необходимо убедиться в следующем:
- в адекватности вида
уравнения модели;
- в статистической значимости
модели регрессии в целом (F-критерий Фишера);
- в статистической значимости
коэффициентов уравнения регрессии и коэффициента корреляции;
- в точности модели (в
качестве меры точности используют оценки значений ошибок).
3.1.
Оценка адекватности уравнения модели
Уравнение модели является адекватным, если:
- математическое ожидание
значений остаточного ряда равно или близко нулю (t-критерий Стьюдента);
- значения остаточного ряда
случайны (критерий пиков);
- значения остаточного ряда
независимы (d-критерий Дарбина-Уотсона);
-
значения остаточного ряда подчинены нормальному закону (R/S-критерий).
а)
t-критерий Стьюдента:
Проверка равенства математического ожидания уровней ряда
остатков нулю осуществляется в ходе проверки статистической нулевой гипотезы Н0
: | eср
| = 0. С этой целью строится t-статистика
t = | eср | * SQR[ n ] / Se
Se = SQR[ n * ånt=1 et2 – ( ånt=1 et ) 2 / ( n * ( n – 1 )) ]
где: eср – среднеарифметическое значение уровней
ряда остатков
et – текущие
значения уровней ряда остатков;
n – длина (количество уровней) ряда;
ånt=1
– операция суммирования значений уровней с номером t в диапазоне от 1 до n;
SQR[ ] – операция извлечения квадратного корня.
Если рассчитанное значение t
< tтабл , то гипотеза Н0 принимается.
Промежуточные результаты расчетов, проведенных для
t-критерия Стьюдента, а также остальных критериев адекватности (рассчитанных в
порядке аналогичном описанному в Задании I), приведены в таблице 8
Таблица 8
|
t
|
Y(t)
|
X1(t)
|
<Y(t)>
|
et
|
точка
поворота
|
et2
|
et
- et-1
|
(et
- et-1
)2
|
et
* et-1
|
et
- eср
|
(et
- eср
)2
|
|
1
|
65
|
29
|
65,34
|
-0,34
|
-
|
0,12
|
-
|
-
|
-
|
-0,48
|
0,23
|
|
2
|
67
|
33
|
62,18
|
4,82
|
1
|
23,23
|
5,16
|
26,63
|
-1,64
|
4,68
|
21,90
|
|
3
|
63
|
32
|
62,97
|
0,03
|
1
|
0,00
|
-4,97
|
22,94
|
0,14
|
-0,11
|
0,01
|
|
4
|
60
|
36
|
59,81
|
0,19
|
1
|
0,04
|
0,16
|
0,03
|
0,01
|
0,05
|
0.00
|
|
5
|
56
|
38
|
58,23
|
-2,23
|
0
|
4,97
|
-2,42
|
5,86
|
-0,42
|
-2,37
|
5,62
|
|
6
|
53
|
41
|
55,86
|
-2,86
|
1
|
8,18
|
-0,63
|
0,4
|
6,38
|
-3
|
9
|
|
7
|
57
|
44
|
53,49
|
3,51
|
1
|
12,32
|
6,37
|
40,58
|
-10,04
|
3,37
|
11,36
|
|
8
|
53
|
42
|
55,07
|
-2,07
|
1
|
4,28
|
-5,58
|
31,14
|
-7,27
|
-2,21
|
4,88
|
|
9
|
51
|
46
|
51,91
|
-0,91
|
-
|
0,83
|
1,16
|
1,35
|
1,88
|
-1,05
|
1,10
|
|
|
|
|
0.14
|
6
|
53,97
|
|
128,93
|
-10,9
|
|
54,1
|
|
|
|
|
eср
|
всего
|
сумма
|
|
сумма
|
сумма
|
|
сумма
|
Se = SQR[ 9 * 53,97 – ( 0,14 ) 2 / ( 9 *
( 9 – 1 )) ] = SQR[485,73 – 0,0196/ 72] = 22,04
t = | 0,14 | * SQR[ 9 ] / 22,04 = 0,0191
Так как рассчитанное значение
t близко к нулю и меньше табличного, например
tтабл (1-a)=0,9 m=7 = 1, 8946, то гипотеза о равенстве нулю математического ожидания значений остаточного
ряда принимается.
б)
критерий пиков:
ркр = 2/3 * ( n – 2) – 1,96 * SQR[(16 * n – 29)
/ 90]
Подставив значение n = 9, получим ркр
= 2,4511. Так как суммарное количество поворотных точек больше критического
значения, то гипотеза о случайности
остаточной компоненты принимается.
в)
d-критерий Дарбина-Уотсона:
d = ånt=2 ( et
- et-1
) 2 / ånt=1 et 2
= 128,93/ 53,97 = 2,39
Так как 2
< d < 4, вычисляем
d` = 4 - d = 1,61
Вычисленное значение d` = 1,61
попадает в зону определенности и модель считается адекватной процессу по
данному критерию.
г) R/S-критерий:
R/S = ( emax – emin ) / Se
Se = SQR[ ånt=1 ( et - eср ) 2 / ( n – 1 ) ]
eср = ( ånt=1
et
) / n
Подставив значения из таблицы
8: emax = 4,82 emin = -2,86 eср
= 0,14 для n = 9 получим
Se = SQR[ 54,1 / 8 ] = 6,7625 » 2,60
R/S = (4,82 – (-2,86)) / 2,60 = 2,95
Так как значение R/S-критерия
попадает в интервал между критическими уровнями 2,7 и 3,7 – то гипотеза о нормальном распределении ряда
остатков принимается.
3.2.
Статистическая значимость модели регрессии в целом (F-критерий Фишера)
F-критерий (F-отношение) Фишера применяется для
установления истинности статистической гипотезы о том, что фактор регрессии
X(t) действительно влияет на зависимую переменную Y(t) или, точнее,
действительно ли часть дисперсии зависимой переменной Y(t) объясняется влиянием
фактора X(t). F-отношение Фишера рассчитывается по формуле
R2 / k
F = ------------------------------------
( 1 – R2 ) / ( n – k – 1 )
где: R2 – коэффициент детерминации;
k – число параметров при переменных, включенных в модель;
n – длина (количество уровней) ряда.
Используя введенные ранее
обозначения, коэффициент детерминации можно записать в виде
R2
= ånt=1
( <Y(t)> – yср ) 2 / ånt=1
( уt – yср ) 2
однако, для однофакторной
модели значение R совпадает с ry,x1 , рассчитанном в первом пункте
задания. Тогда, подставив значения R2 = r2y,x1
= (-0,9) 2 = 0,81 при k = 1 (линейная однофакторная модель) и n = 9,
получим
F =
0,81 / [ ( 1 – 0,81) / ( 9 – 1 –1 ) ] = 0,81 / 0,027 = 30
Табличное значение критерия
Фишера при a
= 0,05 и при степенях свободы k1 = k = 1 и
k2 = n – k – 1 = 7
Fтабл = 5,59
Так как расчетное значение F
> Fтабл , то модель
считается значимой, при этом коэффициент детерминации R2
показывает долю вариации результативного признака под воздействием изучаемого
фактора, т.е. в данном случае ~81% вариации зависимой переменной Y учтено в модели и
обусловлено влиянием включенного фактора X1(t).
3.3.
Статистическая значимость коэффициентов регрессии и корреляции
Оценка значимости коэффициентов регрессии и корреляции
проводится с помощью
t-критерия Стьюдента путем сопоставления значений коэффициентов с величиной
случайной ошибки m
t a1 = a1
/ m a1 t
a0 = a0 / m a0 t
r = r / m r
где
ånt=1 ( Yt –<Y(t)> )
2 / ( n – 2 )
m a1 = SQR [
---------------------------------------------- ]
ånt=1 ( Xt – xср ) 2
ånt=1 ( Yt –<Y(t)> )
2 * ånt=1 Xt 2
m a0 = SQR [
---------------------------------------- ]
( n – 2 )
* n * ånt=1 ( Xt – xср ) 2
1 – r xy 2
m
r = SQR [ ----------------------- ]
n – 2
Промежуточные результаты
вычислений приведены в таблице 9
Таблица 9
|
t
|
Yt
|
Xt
|
<Y(t)>
|
Yt
- <Y(t)>
|
(Yt
- <Y(t)>) 2
|
Xt
- xср
|
(Xt
– xср) 2
|
Xt
2
|
|
1
|
65
|
29
|
65,34
|
-0,34
|
0,12
|
-8,89
|
79,01
|
841
|
|
2
|
67
|
33
|
62,18
|
4,82
|
23,23
|
-4,89
|
23,90
|
1089
|
|
3
|
63
|
32
|
62,97
|
0,03
|
0,00
|
-5,89
|
34,68
|
1024
|
|
4
|
60
|
36
|
59,81
|
0,19
|
0,04
|
-1,89
|
3,57
|
1296
|
|
5
|
56
|
38
|
58,23
|
-2,23
|
4,97
|
0,11
|
0,01
|
1444
|
|
6
|
53
|
41
|
55,86
|
-2,86
|
8,18
|
3,11
|
9,68
|
1681
|
|
7
|
57
|
44
|
53,49
|
3,51
|
12,32
|
6,11
|
37,35
|
1936
|
|
8
|
53
|
42
|
55,07
|
2,07
|
4,28
|
4,11
|
16,90
|
1764
|
|
9
|
51
|
46
|
51,91
|
-0,91
|
0,83
|
8,11
|
65,79
|
2116
|
|
|
37,89
|
|
|
53,97
|
|
270,89
|
13191
|
|
|
xср
|
|
|
сумма
|
|
сумма
|
сумма
|
Тогда при n = 9
m a1 = SQR[53,97/ ( 9 – 2 ) /270,89] = 0,17
m a0 = SQR[53,97/ ( 9 – 2 ) * 13191/ 9 /270,89]
= 6,46
m r = SQR[ ( 1 – 0,81 ) / ( 9 – 2 ) ] = 0,16
и значения t-статистик (по
модулю)
t a1 = 0,881 / 0,17 = 5,18
t a0 = 91,72 / 6,46=14,2
t r = 0,9 / 0,16 = 5,63
Табличное значение t-критерия
Стьюдента при a
= 0,1 и числе степеней свободы n – 2 = 7 составит 1,8946. Так как все
фактические значения t-статистик превышают табличное значение, то коэффициенты регрессии и корреляции
статистически значимы.
3.4.
Оценка точности модели
В качестве меры точности модели регрессии применяют
несмещенную оценку дисперсии остаточной компоненты, т. е. части дисперсии
фактического явления, “не объясненную” включенными в модель факторами.
Стандартная ошибка оценки определяется по формуле
S<Y(t)> = SQR[ ånt=1
( Yt - <Y(t)> ) 2 / ( n – k – 1 ) ]
где: k – количество факторов, включенных в модель ( в данном случае
k=1 );
n – количество уровней ряда.
Из таблицы 9 видно, что ånt=1
( Yt - <Y(t)> ) 2 = 53,97
Тогда
S<Y(t)>
= SQR[53,97 / ( 9 – 2 )] = 2,78
Средняя
относительная ошибка аппроксимации (по модулю), т.е. среднее отклонение
расчетных значений от фактических, определяется по формуле
Еотн
= ( ånt=1
| ( Yt - <Y(t)> ) / Yt | ) / n * 100%
Промежуточные расчетные
данные приведены в таблице 10.
Таблица 10
|
t
|
Yt
|
Xt
|
<Y(t)>
|
Yt -
<Y(t)>
|
(Yt -
<Y(t)>) / Yt
|
| (Yt -
<Y(t)>) / Yt |
|
|
1
|
65
|
29
|
65,34
|
-0,34
|
-0,005
|
0,005
|
|
2
|
67
|
33
|
62,18
|
4,82
|
0,078
|
0,078
|
|
3
|
63
|
32
|
62,97
|
0,03
|
0,00
|
0,00
|
|
4
|
60
|
36
|
59,81
|
0,19
|
0,003
|
0,003
|
|
5
|
56
|
38
|
58,23
|
-2,23
|
-0,038
|
0,038
|
|
6
|
53
|
41
|
55,86
|
-2,86
|
-0,051
|
0,051
|
|
7
|
57
|
44
|
53,49
|
3,51
|
0,066
|
0,066
|
|
8
|
53
|
42
|
55,07
|
2,07
|
0,038
|
0,038
|
|
9
|
51
|
46
|
51,91
|
-0,91
|
-0,018
|
0,018
|
|
|
|
|
|
|
0,297
|
|
|
|
|
|
|
сумма
|
Окончательно: Еотн = 0,297 / 9 * 100% =
3,3%
Так как Еотн <
5%, то модель считается точной.
4) Коэффициент эластичности и b-коэффициент.
Коэффициент эластичности (т.е. коэффициент, показывающий
на сколько процентов изменится результат, если фактор изменится на 1%) в общем
виде определяется как
x
Э = ƒ΄(x) * ------
y
где: ƒ΄(x) – первая производная функции y = ƒ(x).
Так как для линейной функции
коэффициент эластичности зависит от значения фактора Х, то воспользуемся
формулой среднего коэффициента эластичности
x ср
Э ср = а1 * ---------------------
а0 + а1 * х ср
Подставив
вычисленные ранее значения, получим
Э ср = -0,881* 37,89/ (91,72– 0,881 *37,89) = - 0,27 %
Стандартизованный b-коэффициент линейной
регрессии определяется из общего уравнения множественной регрессии в
стандартизованном масштабе
t y = b 1 * t x1 + b 2 * t x2 + … + b N * t xN
где: t y = ( y - y ср ) / s
y , t Xj = ( x j
- x j ср ) / s Xj - стандартизованные переменные;
b j - стандартизованные коэффициенты
регрессии, определяемые из системы уравнений
r y x1 = b 1 +
b 2 * r x2 x1
+ … + b N * r xN x1
r y x2 = b 1 * r x2 x1 + b 2 + … + b N * r xN x1
………………………………………………………….
r y xN = b 1 * r xN
x1 + b 2 * r xN
x2 + … + b
N
где: r y Xj – парные коэффициенты корреляции.
Для однопараметрической (однофакторной) линейной модели
регрессии система уравнений сводится к тождеству
r y x1 = b 1
отсюда значение b-коэффициента
линейной однофакторной регрессии: b
1 = -0,9.
2-й способ:
из сопоставления систем уравнений множественной регрессии
(для метода наименьших квадратов) в нормальной линейной и стандартизованной
формах также известно, что связь между коэффициентами b i и
коэффициентами множественной регрессии b i выражается соотношением
b
i = b i * s x / s y
где: s - среднеквадратическое отклонение.
Для линейной однопараметрической регрессии коэффициент b 1
совпадает с коэффициентом а 1 линии регрессии.
Эмпирическое среднеквадратическое
отклонение вычисляется по формуле
S z = SQR[ ånt=1 ( z t – z cp ) 2
/ ( n – 1 ) ]
где: n – длина эмпирического ряда.
Тогда, используя данные из
таблицы 4
ånt=1
( X 1t – x cp ) 2 = 270,89и ånt=1 ( z t – z
cp ) 2 = 262,00
для
n = 9 получим
S x = SQR[270,89/ 8 ] = 5,82
S y = SQR[
262,00 / 8 ] = 5,72
b 1 = а 1 * S x / S y = -0,881 *
5,82/ 5,72 = -0,895»-0,9
5) Точечный и интервальный прогнозы.
Прогнозируемое точечное значение переменной Y(t) для
периода упреждения на k = 2 шага вперед получается при подстановке в уравнение
регрессии ожидаемой величины фактора X1(t) при tпрогноз =
n + k , т.е.
<Y(t=
tпрогноз)> =91,72– 0,881* X1(t= tпрогноз)
Получим прогнозные оценки фактора
X1(t) на основе величины его среднего абсолютного прироста (САП)
САП = [ X1(t=n) – X1(t=1) ] / ( n –
1 )
X1 прогноз (t=n+k) = X1(t=n) + k *
САП
Подставив соответствующие
значения, получим
САП
= ( 46 – 29) / 8 = 2,125
Тогда
прогнозные значения фактора X1(t)
X1
прогноз(10) = X1(9) + 1 * САП = 46 + 2,125 = 48,125
X1 прогноз(11) = X1(9) + 2 * САП =
46 + 4,25 = 50,25
И
прогнозные значения зависимой переменной
<Y(10)> = 91,72– 0,881 * 48,125 = 49,32
<Y(11)>
= 91,72– 0,881 * 50,25 = 47,45
Интервальный прогноз
рассчитывается с помощью доверительных интервалов по формуле
<Y(tпрогноз)> ± U(k)
где: U(k)
– средняя стандартная ошибка прогноза
( x прогноз (n+k) – x ср )
2
U(k) = S<Y(t)> * t a * SQR[ 1 + 1/n +
----------------------------- ]
ånt=1
( x t – x ср ) 2
S<Y(t)> -
стандартная ошибка оценки;
t a
– табличное значение критерия Стьюдента для числа степеней свободы ( n – 2 ).
Подставив известные (по
условию задачи) значения n = 9 и t 0,7 = 1,11 ; а также вычисленные
ранее значения S<Y(t)> = 2,78 (пункт 3.4) ; x1ср =
37,88 и ånt=1
(X1t - x1ср) 2 = 270,89(таблица 4), получим
U(1) = 2,78* 1,11 * SQR[ 1 + 1/9 + (48,125 – 37,89) 2 /270,89]
= 3,76
U(2) = 2,78* 1,11 * SQR[ 1 + 1/9 + (50,25 –37,89) 2 /270,89] =
3,98
Результаты прогнозных оценок
по линейной однофакторной модели регрессии представлены в таблице 11
Таблица 11
|
t
|
шаг k
|
прогноз <Y(tпрогноз
)>
|
нижняя граница
|
верхняя граница
|
|
10
|
1
|
49,32
|
45,56
|
53,08
|
|
11
|
2
|
47,45
|
43,47
|
51,43
|
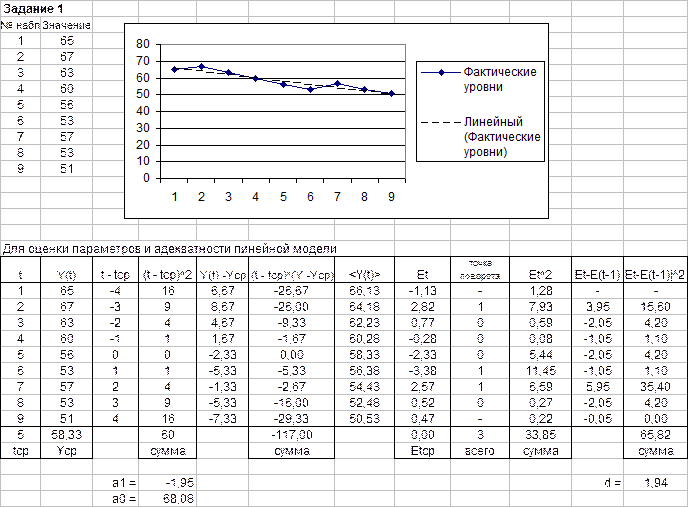
Рис.1Б. График линейной модели тренда с результатами
прогнозирования
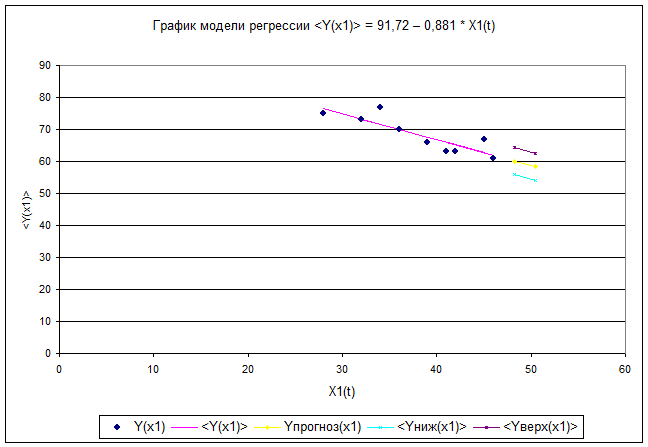
Рис.2 График линейной однофакторной модели регрессии с
результатами прогнозирования