Федеральное агентство по образованию
Всероссийский заочный
финансово-экономический институт
Кафедра экономико-математических методов и моделей
Контрольная
работа по дисциплине
«Финансовая математика»
Вариант № 4
Волгоград 2009
Задание 1.
Приведены поквартальные
данные о кредитах от коммерческого банка на жилищное строительство (в условных
единицах) за 4 года (всего 16 кварталов, первая строка соответствует первому
кварталу первого года).
|
Квартал
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
|
Данные о кредитах,
у.е.
|
33
|
42
|
50
|
33
|
36
|
46
|
56
|
34
|
39
|
50
|
59
|
37
|
44
|
54
|
65
|
40
|
Требуется:
1). Построить адаптивную
мультипликативную модель Хольта-Уинтерса с учетом сезонного фактора, приняв
параметры сглаживания 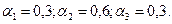
2). Оценить точность
построенной модели с использованием средней относительной ошибки аппроксимации.
3). Оценить адекватность
построенной модели на основе исследования:
ü Случайности остаточной компоненты по
критерию пиков;
ü Независимости уровней ряда остатков
по d-критерию (критические
значения 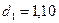 и
и 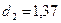 ) и по первому коэффициенту автокорреляции при критическом
значении
) и по первому коэффициенту автокорреляции при критическом
значении  .
.
ü Нормальности распределения остаточной
компоненты по R/S-критерию с критическими значениями от 3 до 4,21.
4). Построить точечный
прогноз на 4 шага вперед, то есть на 1 год.
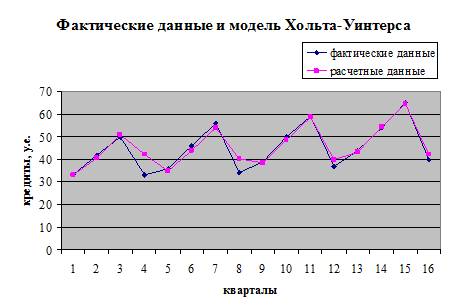
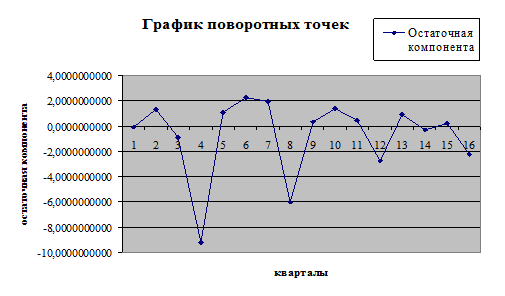
5). Отразить на графике
фактические, расчетные и прогнозные данные.
1. 1).
Построим адаптивную модель Хольта-Уинтерса.
Для первых восьми
наблюдений построим график, добавим линейный тип тренда и в параметрах поставим
галочку «Показывать уравнение»:
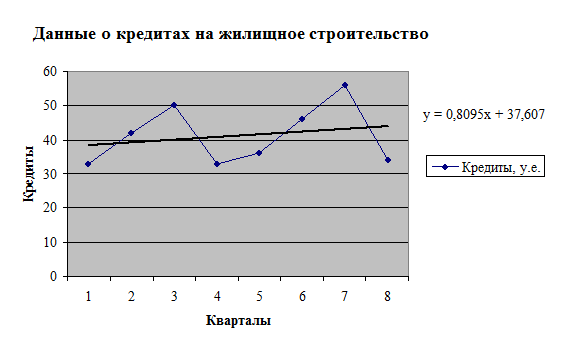
Таким
образом мы получили 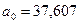 и
и 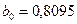 .
.
Подставив
эти значения в формулу 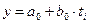 , рассчитаем первые 7
значений линейной функции.
, рассчитаем первые 7
значений линейной функции.
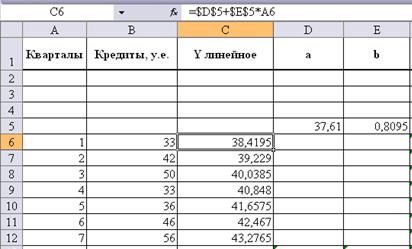
Далее
заполняем первую строку столбца значений коэффициентов сезонности 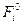 , скопировав ее затем еще на три строки:
, скопировав ее затем еще на три строки:
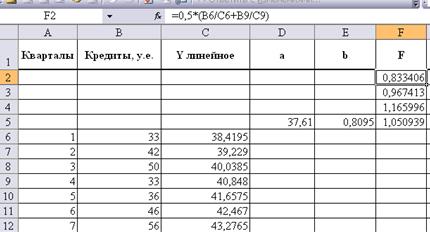
Затем
заполняем формулами шестые строки столбцов параметров модели 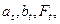 Y (Хольта-Уинтерса),
Y (Хольта-Уинтерса), 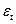 :
:
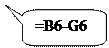
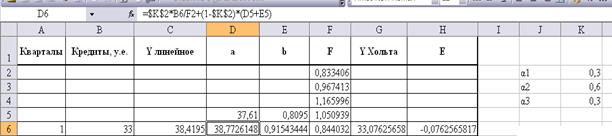



Затем, выделив интервал D6:H6, копируем все вместе до 21 строки:
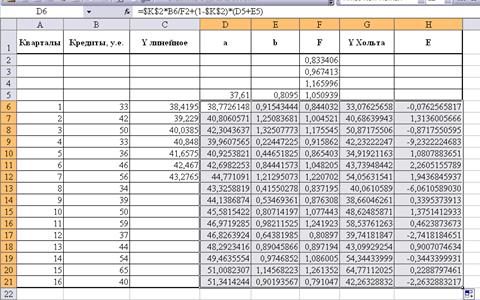
2). Оценим точность построенной модели:
Рассчитаем среднюю
относительную ошибку аппроксимации. Для этого найдем сумму значений 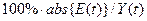 :
:
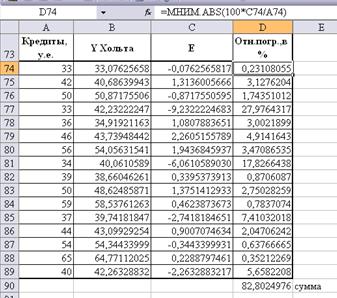
82,8024976/16=5,18%>5%,
значит условие точности не выполнено и модель построена не совсем точно.



3). Оценим адекватность
построенной модели:
Исследуем случайность
остаточной компоненты по критерию пиков.
Сравнивая каждое значение
остаточной компоненты с рядом стоящими, ставим 1, если оно больше или меньше
обоих значений, в противном случае 0:
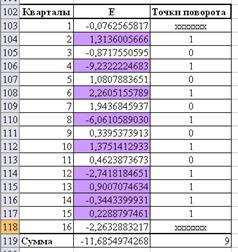
Таким образом, мы
получили 9 поворотных точек, то есть p=9. Рассчитаем q:
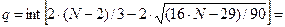
 .
.
Итак, p=9, q=6, 9>6, значит условие
случайности уровней ряда остатков выполнено.
Оценим адекватность
построенной модели Хольта-Уинтерса по d-критерию и по первому коэффициенту
автокорреляции.
Для вычисления этих
показателей, осуществим следующие расчеты:
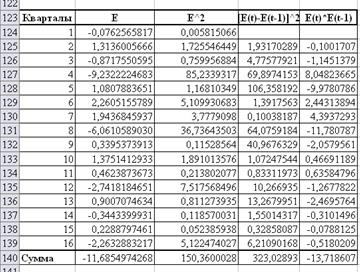
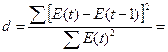
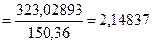 .
.
2,148>2,значит имеет место отрицательная
автокорреляция
То есть d = 4 – 2,148 = 1,852.
Итак, 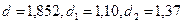 .
.
1,37<1,85<2, то есть 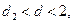 значит уровни ряда
остатков являются независимыми.
значит уровни ряда
остатков являются независимыми.
Далее рассчитаем значение
первого коэффициента автокорреляции по следующей формуле:
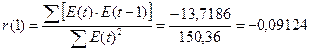 .
.
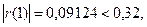 значит уровня ряда
остатков независимы.
значит уровня ряда
остатков независимы.
Исследуем нормальность
распределения остаточной компоненты по R/S-критерию.
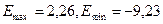 ,
, 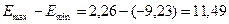 .
.
 .
.
R/S=11,49 / 3,16607 = 3,62996/
Так как
3<3,63<4,21, то полученное значение R/S попало в заданный интервал. Значит,
уровни ряда остатков подчиняются нормальному распределению.
4). Построим точечный
прогноз на 4 шага вперед, то есть на год:
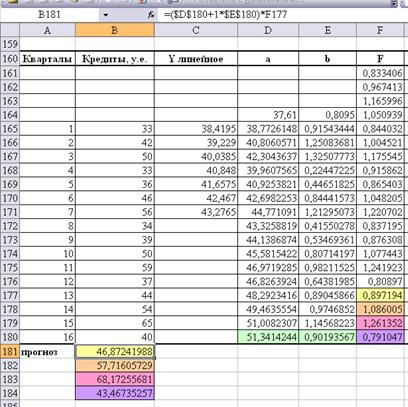 Таким образом, прогнозное значение
Таким образом, прогнозное значение 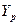 =
=
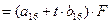 , где t=1,…4, а F=
, где t=1,…4, а F=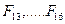 .
.
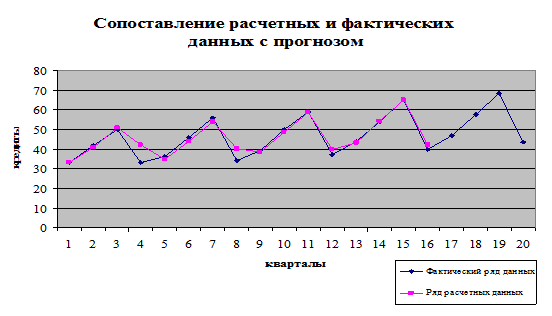
Изобразим на графике
расчетные, фактические данные и прогнозные значения.
Задание 2.
Даны цены за 10 дней.
Интервал сглаживания принять равным пяти дням. Рассчитать:
ü Экспоненциальную скользящую среднюю;
ü Момент;
ü Скорость изменения цен;
ü Индекс относительной силы;
ü %R, %K и %D.
|
Дни
|
Цены
|
|
макс
|
мин
|
закр
|
|
1
|
744
|
705
|
709
|
|
2
|
743
|
675
|
738
|
|
3
|
750
|
700
|
735
|
|
4
|
759
|
707
|
751
|
|
5
|
770
|
740
|
755
|
|
6
|
776
|
661
|
765
|
|
7
|
756
|
715
|
720
|
|
8
|
745
|
685
|
739
|
|
9
|
758
|
725
|
740
|
|
10
|
730
|
673
|
678
|
Чтобы рассчитать ЕМА,
воспользуемся формулой:
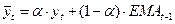
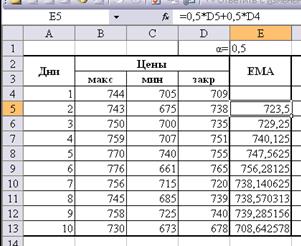
Далее по соответствующим
формулам вычисляем момент и скорость изменения цен:

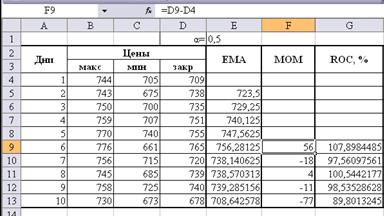
Чтобы рассчитать индекс
относительной силы, необходимо для начала найти прибыли, убытки, а затем их суммы:
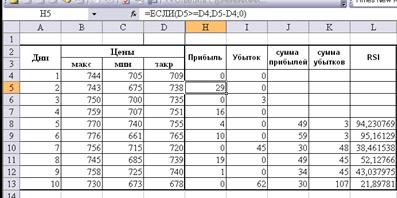
С помощью функции «ЕСЛИ»
задаем условие: если разность сегодняшней и вчерашней цен положительна, то
будет прибыль, а если отрицательна – убыток. Суммы прибылей и убытков находим
группируя по 5 дней. Индекс находится по формуле: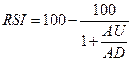 .
.
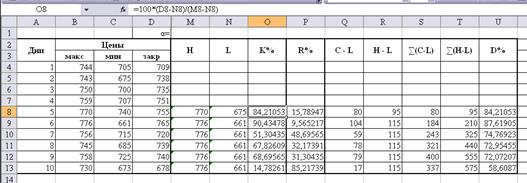
По найденным осцилляторам
можно сделать следующие выводы:
ü Так как на шестой день момент
положительный, то в этот промежуток времени наблюдался относительный рост цен,
далее снижение.
ü Показатель индекса относительной силы
до шестого дня входил в зону перекупленности, что означало завышенные цены и
тенденцию к их занижению; значение индекса на десятый день 21,89 говорит о
вхождении в зону перепроданности, цена очень низкая, надо готовиться к покупке.
Найдем стохастики:
 .
.
Уменьшение значений
стохастика %К от пятого до десятого дня говорит о том, что сначала при росте цен
цена закрытия была ближе к максимальной, а затем при падении цен стала ближе к
минимальной.
Задание 3.
1. Банк выдал ссуду,
размером 2 000 000 руб. Дата выдачи ссуды -16.01.2002, возврата – 14.03.2002.
День выдачи и день возврата считать за 1 день. Проценты рассчитываются по
простой процентной ставке 25% годовых. Найти:
1). Точные проценты с
точным числом дней ссуды;
2). Обыкновенные проценты
с точным числом дней ссуды;
3). Обыкновенные проценты
с приближенным числом дней ссуды.
Решение:
Срок сделки найдем с
помощью функции в Excel «Долягода», а проценты по формуле I=Pni:
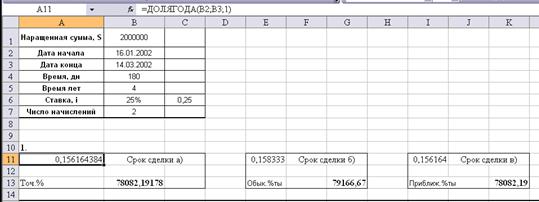
2. Через 180 дней после
подписания договора должник уплатит 2 000 000 руб. Кредит выдан под 25% годовых
(проценты обыкновенные). Какова первоначальная сумма и дисконт?
Решение:
P=S / (1+ni) = 2000000 / (1+0,5*0,25) = 1777777,78
руб.
D = S – P = 2000000
- 1777777,78 = 222222,22 руб.
3. Через 180 дней
предприятие должно получить по векселю 2 000 000 руб. Банк приобрел этот
вексель с дисконтом. Банк учел вексель по учетной ставке 25% годовых (год равен
360 дням). Определить полученную предприятием сумму и дисконт.
Решение:
D = Snd = 2000000*0,5*0,25 = 250000 руб.
P = S – D = 2000000
– 250000 = 1750000 руб.
4. В кредитном договоре
на сумму 2 000 000 руб. и сроком на 4 года, зафиксирована ставка сложных
процентов, равная 25% годовых. Определить наращенную сумму.
Решение:
Данную задачу можно
решить используя функцию Excel «БС»:
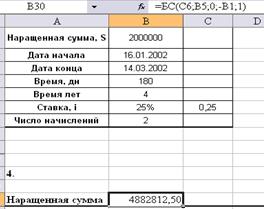
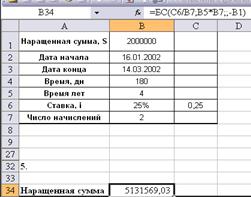
5. Ссуда, размером 2 000
000 руб. предоставлена на4 года. Проценты сложные, ставка – 25% годовых.
Проценты начисляются 2 раза в году. Вычислить наращенную сумму.
Решение:
Также используя функцию
«БС» найдем наращенную сумму:
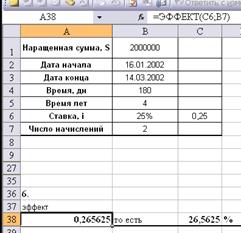
6. Вычислить эффективную
ставку процента, если банк начисляет проценты 2 раза в году, исходя из
номинальной ставки 25% годовых.
Решение:
Используя функцию Excel «ЭФФЕКТ», найдем ставку:
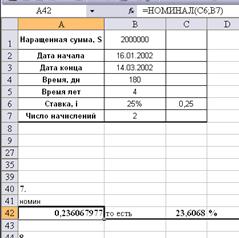
7. Определить, какой
должна быть номинальная ставка при начислении процентов 2 раза в году, чтобы
обеспечить эффективную ставку 25% годовых.
Решение:
Для вычисления
номинальной ставки используем функцию «НОМИНАЛ»:
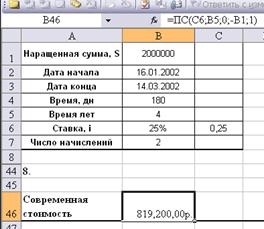
8. Через 4 года
предприятию будет выплачена сумма 2 000 000 руб. Определить ее современную
стоимость при условии, что применяется сложная процентная ставка 25% годовых.
Решение.
Используя функцию «ПС»,
найдем современную стоимость:
9. Через 4 года по
векселю должна быть выплачена сумма 2 000 000 руб. Банк учел вексель по сложной
учетной ставке 25% годовых. Определить дисконт.
Решение:
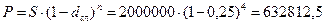 руб.
руб.
D = S – P = 2 000 000 – 632 812,5 = 1367187,5
руб.
10. В течение 4 лет на
расчетный счет в конце каждого года поступает по 2 000 000 руб., на которые 2
раза в году начисляются проценты по сложной годовой ставке 25%. Определить
сумму на расчетном счете к концу указанного срока.
Решение:
Расчеты производим
используя функцию «БС»:
