Содержание
Задача 1. 3
Задача 2. 5
Задача 3. 9
Задача 4. 12
Задача 5. 14
Задача 6. 16
Задача 7. 18
Список использованной литературы.. 20
Задача 1
Основные показатели бюджета
региона характеризуются следующими данными (млн.руб.):
|
Показатель
|
Базисный
период
|
Отчетный
период
|
|
Доходы
– всего
В том
числе:
|
1415
|
2520
|
|
Налоговые
|
1205
|
2215
|
|
Неналоговые
|
210
|
305
|
|
Расходы
– всего:
В том
числе:
|
1380
|
2610
|
|
Социально-культурные
мероприятия
|
480
|
980
|
|
Государственная
поддержка отраслей экономики
|
435
|
1230
|
Определите все возможные виды
относительных величин. Сделайте выводы.
Решение:
1. Одним из первых видов относительных величин – нахождение доли
(%) или относительного
показателя координации (ОПК) в процентном выражении. Данные
показатель показывают, на какой процент доля доходов в бюджете отличаются от доли расходов.
Определим долю расходов в сумме
доходов:
Dr 1 (ОПК) = 1380*100/1415 = 97,5.
Dr 2 (ОПК) = 2610*100/2215 =
103,6.
Таким образом, в бюджетный период
доля доходов в бюджете превышает долю расходов на 2,5 (100% - 97,5%). В
отчетном периоде доля расходов превысила долю доходов на 3,6 (103,6% – 100%).
Определим долю расходов на
социально-культурные мероприятия в сумме доходов:
Dr соц.1 (ОПК) = 480*100/1415 = 33,9.
Dr соц.2 (ОПК) = 980*100/2520 = 38,9.
Таким образом, в базисном и
отчетном периоде доля расходов на социально-культурные мероприятия составили
небольшой процент на общую долю доходов, т.е. процент разницы составил
соответственно 66,1 (100% - 33,9%) и
61,1 (100% - 38,9).
Определим долю расходов на
государственную поддержку отраслей экономики в сумме доходов:
Dr гос.1 (ОПК) = 435*100/1415 = 30, 7.
Dr гос.2 (ОПК) = 1230*100/2520 = 48, 8.
Таким образом, в базисном и
отчетном периоде доля расходов на государственную поддержку отраслей экономики составили
небольшой процент на общую долю доходов, т.е. процент разницы составил
соответственно 69,3 (100% - 30,7) и 51,2
(100% - 48,8%).
Таким образом, мы видим, что доля
общих расходов на сумму доходов в отчетном году увеличилась на 6,1%, при этом
доля расходов на государственную
поддержку отраслей экономики в отчетном периоде возросла на 18,1% по сравнению
с базисным периодом, а на социально-культурные мероприятия увеличилась на 5%.
Найдем другие виды относительных
величин:
2. Относительный
показатель динамики (ОПД).
Фактический показатель текущего периода
Фактический показатель базисного периода
Найдем ОПД для доходов. Исходя
из формулы, ОПД1
= 2520/1415 = 1,8.
Найдем ОПД для расходов. Исходя
из формулы, ОПД2
= 2610/1380 = 1,9.
Найдем ОПД для общего бюджета.
Исходя из формулы, ОПД3 = (2520 + 2610)/(1415 + 1380) = 5130/2795 = 1,8.
Таким образом, по данному
показателю видно, что в отчетном периоде
наблюдается динамика роста показателей доходов и расходов, общего
бюджета в целом.
3. Относительный показатель
структуры (ОПС).
Показатель, характеризующий часть совокупности
Показатель, характеризующий всю совокупность
Найдем ОПС для расходов бюджета
региона.
Найдем долю налоговых доходов в
общей сумме доходов за базисный и отчетный периоды:
ОПС1б = 1205/1415 = 0,9; ОПС1о = 2215/2520
= 0,9.
Найдем долю неналоговых доходов
в общей сумме доходов за базисный и отчетный периоды:
ОПС2б = 210/1415 = 0,2; ОПС2о = 305/2520 =
0,1.
Найдем
долю расходов на социально-культурные мероприятия в общей сумме расходов за
базисный и отчетный периоды:
ОПС3б = 480/1380 = 0,4; ОПС3о = 980/2610 = 0,4.
Найдем
долю расходов на государственную поддержку отраслей экономики в общей сумме
расходов за базисный и отчетный периоды:
ОПС4б = 435/1380 = 0,3; ОПС4о = 1230/2610 = 0,5.
Таким образом, по данному
показателю видно, что доли налоговых и неналоговых доходов в общей сумме
доходов в базисный и отчетный период мало изменились. Также остались неизменны
в базисный и отчетный период доли расходов на социально-культурные мероприятия
в общей сумме расходов. Изменилась доля расходов на государственную поддержку
отраслей экономики в общей сумме расходов за базисный и отчетный периоды на
0,2.
Задача 2
Возраст работников коммерческой
фирмы представлен следующими данными:
|
24
|
18
|
20
|
30
|
33
|
28
|
26
|
32
|
37
|
41
|
|
36
|
19
|
23
|
34
|
24
|
29
|
39
|
36
|
30
|
25
|
|
32
|
22
|
28
|
38
|
40
|
21
|
35
|
42
|
26
|
30
|
Определите средний возраст
работников коммерческой фирмы, дисперсию и коэффициент вариации возраста
сотрудников фирмы:
А) на основе дискретного ряда
распределения;
Б) на основе построенного интервального
ряда (5 интервалов).
Решение:
Составим дискретный ряд
распределения возрастов работников на основе частоты встречаемости каждого из
возрастов:
18 лет – 1 работник; 19 – 1; 20 –
1; 21 – 1; 22 – 1; 23 – 1; 24 – 2; 25 – 1; 26 – 2; 28 – 2; 29 – 1; 30 – 3; 32 –
2; 33 – 1; 34 – 1; 35 – 1; 36 – 2; 37 – 1; 38 -1; 39 – 1; 40 – 1; 41 – 1; 42 –
1. Таким образом, в распределении получилось 22 группы.
Определим средний возраст
работников на основе дискретного ряда распределения:
V’ = ∑V/Q,
Где V –
возраст
Q – количество
работников.
V’ = 898/30 = 29.
Определим дисперсию с помощью
дискретного ряда распределения:
D = ∑V*n/∑n,
Где n – частота встречаемости
данного элемента.
D = 18*1 + 19*1 + 20*1 + 21*1 + 22*1 + 23*1 +
24*2 + 25*1+ 26*2 + 28*2 + 29*1 + 30*3 + 32*2 + 33*1 + 34*1 + 35*1 + 36*2 +
37*1 + 38*1 + 39*1+ 40*1 + 41*1 + 42*1/22 = 898/22 = 40,8.
Определим коэффициент вариации с
помощью дискретного ряда распределения:
Кв = D/ V’ = 40,8/29 = 1,4.
2. Составим
интервальный ряд.
Для этого распределим все данные возрастов работников на 5
интервалов в соответствии с этапом их жизни, а именно – становление личности,
молодость, возраст вступления в брак, возраст выполнения общественных
обязанностей, возраст познания собственных заблуждений.
Таким образом, получим пять интервалов:
до 20 лет - становление личности;
до 25 лет - молодость;
до 30 лет - возраст вступления в брак;
до 40 лет - возраст выполнения общественных обязанностей;
до 50 лет - возраст познания собственных заблуждений;
Интервалы будут выглядеть
следующим образом:
1.До 20 лет: 18 и 19, 20 – 3 работника;
2.До 25 лет: 21, 22, 23, 24, 25 –
6 работников;
3.До 30 лет: 26, 28, 29, 30 – 8
работников;
4.До 40 лет: 32, 33, 34, 35, 36,
37, 38, 39, 40 – 11 работников;
5.До 50 лет: 41, 42 – 2
работника.
Определим средний возраст
работников в на основе интервального ряда:
V’ = ∑ V/n,
Где V –
возраст
n – количество интервалов.
V’ = 898/5 = 179, 6.
Определим дисперсию с помощью
интервального ряда:
D = ∑ V*n/∑n,
Где n – номер интервала.
D = 2*1 + 6*2 + 8*3 + 11*4 + 2*5/1+2+3+4+5 = 92/15
= 6,1.
Определим коэффициент вариации с
помощью интервального ряда распределения:
Кв = D/ V’ = 6,1/179,6 = 0,03.
Таким образом, данные,
полученные с помощью дискретного ряда отличаются от данных полученных с помощью
интервального ряда, так как в интервальном ряду используется группировка
данных, а в дискретном ряду учитывается каждое значение.
Задача 3
Используя взаимосвязь
показателей, определите недостающие в таблице данные о прибыли в регионе:
|
Год
|
Прибыль, млн.руб.
|
Цепные показатели динамики
|
|
Абсолютный прирост, млн.руб.
|
Темп роста, %
|
Абсолютное содержание одного
процента прироста, млн.руб.
|
|
2000
|
552
|
-
|
-
|
-
|
|
2001
|
580
|
28
|
105
|
5,52
|
|
2002
|
600
|
20
|
103,4
|
5,8
|
|
2003
|
615
|
15
|
102,5
|
6
|
По полученным результатам
исчислите среднегодовой абсолютный прирост и среднегодовой темп прироста
прибыли в 2000-2003 гг.
Решение:
Определим прибыль в 2001 г. Так
как абсолютный прирост в 2001 году составил 28, то найдем прибыль в
соответствующем году, исходя из формулы:
∆1
= Yi-Yi-1.
28 = Y1 – 552.
Следовательно, Y1 = 580.
Определим коэффициент роста в
2001 году: Кр = Yi/Yi-1 = 1,05. Следовательно,
темп роста составит: Тр. = Кр. * 100 = 105.
Теперь по формуле абсолютного
значения одного процента прироста найдем прибыль в 2002 год: Y2 = I*100 = 600.
Исходя из формулы, темпа роста,
найдем прибыль в 2003 году: Кр. = Y3/ 600; Тр. = (Y3/
600)*100; Y3 =
600*102,5/100 = 615.
Теперь определим абсолютный
прирост: в 2002г. ∆2 = 20; в 2003г. ∆3 = 15.
Найдем темп роста в 2002 году:
Кр. = 1,034; Тр. = 1,034*100 = 103,4.
По полученным данным о прибыли в
регионе, найдем среднегодовой абсолютный прирост в 2000-2003 гг.:
∆’
= ∑∆ц/n,
Где n – число
абсолютных цепных приростов.
Исходя из формулы, ∆’ =
63/3 = 21 млн. руб.
Среднегодовой абсолютный прирост
в 2000-2003 гг. можно рассчитать с помощью другой формулы:
∆’
= (yn – y0)/(n-1),
где yn и y0 – прибыль соответственно за последний и первый год,
n – количество
годов.
Исходя из формулы, ∆’ = (615 – 552)/(4-1) = 63/3 = 21
млн. руб.
Найдем среднегодовой темп прироста прибыли в 2000-2003
гг.:
Т’пр.
= 
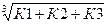*100.
Найдем коэффициенты прироста: К1
= Кр.1 –
1 = 0,05; К2 = Кр.2
– 1 = 0,034; К3 = Кр.3 – 1 = 0,025.
Исходя из формулы, Т’пр. = 3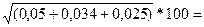
0,48*100 = 48%.
Также средний темп прироста можно найти по другой формуле,
исходя из среднего темпа роста:
Т’пр
= Т’р – 100 %
Где Т’р = 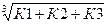*100% = 3
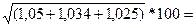1,48*100 = 148%.
Тогда Т’пр = 148% –
100% = 48%.
Таким образом, по полученным
данным, следует сделать вывод, что прибыль в период 2000 – 2003гг. растет,
показатели абсолютного прироста и темпа роста снижаются, а показатель абсолютного содержания одного
процента прироста растет. При этом среднегодовой абсолютный прирост в
2000-2003 гг. составил 21 млн.руб., а среднегодовой темп прироста прибыли в
2000-2003 гг. – 48%.
Задача 4
Имеются данные о продаже товаров
в универсаме:
|
Группа товаров
|
Продано в базисном периоде, тыс.
руб.
|
Соотношение количества проданных
товаров в отчетном периоде по сравнению с базисным
|
|
Молочные
продукты
|
150
|
1,01
|
|
Колбасные
изделия
|
280
|
1,05
|
|
Хлебобулочные
изделия
|
70
|
1,02
|
Определите, как изменились:
1)физический объем реализации
всех товаров в отчетном периоде по сравнению с предыдущим;
2)цены на товары, если известно,
что объем товарооборота в отчетном периоде увеличился на 12%.
Сделайте выводы.
Решение:
Определим физический объем реализации в отчетном периоде:
Vо = Vб * S,
где Vб –
объем реализованной продукции в базисном периоде,
S – соотношение количества проданных товаров в отчетном
периоде по сравнению с базисным.
Исходя из формулы, Vо1 = 150*1,01 = 151,5 тыс. руб.; Vо2
= 280*1,05 = 294 тыс.
руб.; Vо3 = 70*1,02 =
71,4 тыс. руб.
Таким образом, по сравнению с
базисным годом, в отчетном году объем реализации изменился следующим образом:
∆V = Vо – Vб.
Исходя из формулы, ∆V1 = 151,5 – 150 = 1,5 тыс.руб.; ∆V2 = 294 – 280 = 14 тыс. руб.; ∆V3 = 71,4 – 70 = 1,4 тыс.руб.
Найдем товарооборот за базисный
год:
ТОб = Vб1
+ Vб2 + Vб3.
ТОб = 150+280+70 = 500 тыс.руб.
Таким образом, исходя из
условия, товарооборот в отчетном году составит: ТОо = 500 + 500*12% = 560 тыс.
руб.
Определим цены на товары по
формуле:
p = TO/q,
где q –
количество проданных товаров в соответствующем году.
Исходя из формулы, найдем цены на
товары в базисном году pб1 = 500/150 = 3,3; pб2 = 500/280 = 1,8; pб3 = 500/70 = 7,1.
Исходя из формулы, найдем цены на
товары в отчетном году pо1 = 560/151,5 = 3,7; pо2 = 560/294 = 1,9; pо3 = 560/71,4 = 7,8.
Таким образом, по сравнению с
базисным годом, в отчетном году цена на товар изменилась следующим образом: ∆р
= ро – рб.
Исходя из формулы, ∆р1 = 3,7-3,3 =
0,4; ∆р2
= 1,9-1,8 = 0,1; ∆р3 = 7,8-7,1=0,7.
Таким образом, как цены, так и
количество реализованной продукции в отчетном году возросли. В отчетном году наиболее
возрос объем реализации колбасных изделий на 14 тыс.руб., при том, что цена
изменилась незначительно, на 0,1. Незначительный рост произошел в объеме
реализации молочных продуктов и хлебобулочных изделий в отчетном году
соответственно на 1,5 тыс. руб. и 1,4
тыс. руб. При том, что цена на данные товары увеличилась на 0,4 на молочные
продукты и на 0,7 на хлебобулочные изделия.
Задача 5
Предприятия одной из отраслей
промышленности реализовали в базисном году продукции на сумму 62 трлн.руб., при
среднегодовой стоимости оборотных средств в 21 трлн.руб. В отчетном году эти
предприятия реализовали продукции на 68,2 трлн.руб., а число оборотов оборотных
средств увеличилось на 0,35.
Определите, какую сумму
оборотных средств высвободили данные предприятия в результате ускорения
оборачиваемости оборотных средств.
Решение:
Найдем коэффициент
оборачиваемости материальных оборотных средств:
Коб.
= РП/S,
где РП – количество реализованной продукции,
S - среднегодовая стоимость оборотных
средств.
Исходя из формулы:
Коб.б
= 62/21= 2,95.
Коб.о.
= 2,95 + 0,35 = 3,3.
Исходя из формулы коэффициента
оборачиваемости материальных оборотных средств, среднегодовая стоимость
материальных оборотных средств в отчетном году составит:
S = РПо./Коб.о. = 68,2/3,3 =
21,7.
Найдем коэффициент закрепления
материальных оборотных средств:
Кзакр.
= S/РП.
Исходя из формулы:
Кзакр.б.
= 21/62 = 0,34.
Кзакр.о.
= S/РП = 0,36.
Найдем сумму средств,
высвобожденных из оборота в результате ускорения:
∆О
= (Кзакр.1-Кзакр.0)*РП1,
где Кзакр.1и Кзакр.0 – коэффициенты закрепления
соответственно за отчетный и
базисный годы,
РП1 – количество реализованной
продукции за отчетный период.
∆О
= (0,36 – 0,34)*68,2 = 0,02*68,2 = 1,36 трлн.руб.
Таким образом, количество
высвобожденных материальных оборотных средств составили: 1,36 трлн.руб.
Задача 6
Имеются следующие данные о
денежных доходах и расходах населения одного из регионов (в среднем на душу
населения):
|
Базисный
|
Отчетный
|
|
Всего
доходов
|
17815
|
48600
|
|
Всего
расходов:
В том
числе:
|
17580
|
47560
|
|
Покупка
товаров и оплата труда
|
11600
|
38800
|
|
Расходы
населения на приобретение иностранной валюты
|
5600
|
8200
|
Определите коэффициенты
эластичности расходов населения региона с изменением доходов:
А) по всем расходам населения;
Б) по расходам, связанным с
покупкой товаров и услуг;
В) по расходам на приобретение
иностранной валюты.
Сделайте выводы.
Решение:
Коэффициент эластичности
находится по формуле:
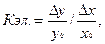
где y0 и y1 – уровень потребления соответственно в
базисном и
отчетном периоде;
∆y - уровень потребления в отчетном периоде по
сравнению с базисным, т.е. ∆y = y1 - y0;
x0 и x1
– среднедушевой доход соответственно в базисный и отчетный период;
∆x – изменение среднедушевого дохода за
истекший
период, т.е. ∆x = x1 - x0.
Исходя из формулы, найдем
коэффициент эластичности расходов населения региона с изменением доходов по
всем расходам населения:
Кэл.1 = ((47560
-17580)/17580)/((48600 – 17815)/17815 = 1,71/1,73 = 0,99.
Найдем коэффициент эластичности
расходов населения региона с изменением доходов по расходам, связанным с
покупкой товаров и услуг:
Кэл.2 = ((38800
– 11600)/11600)/((48600 – 17815)/17815 = 2,3/1,7 = 1,4.
Найдем коэффициент эластичности
расходов населения региона с изменением доходов по расходам на приобретение
иностранной валюты:
Кэл.2 = ((8200 –
5600)/5600)/((48600 – 17815)/17815 = 0,5/0,7 = 0,7.
Так как коэффициент эластичности
показывает относительное изменение исследуемого параметра системы под действием
единичного относительного изменения некоторого фактора, то, проанализировав три
полученных коэффициента эластичности, можно сказать, что наибольшим является коэффициент
эластичности расходов населения региона с изменением доходов по расходам,
связанным с покупкой товаров и услуг, что говорит о значительном изменении
данного показателя под действием изменения доходов; а наименьшим - коэффициент
эластичности расходов населения региона с изменением доходов по расходам на приобретение
иностранной валюты, что говорит о незначительном изменении данного показателя
под действием изменения доходов.
Задача 7
Имеются следующие данные по
предприятию (тыс.руб.):
|
Показатель
|
Базисный
период
|
Отчетный
период
|
|
Выручка от реализации продукции
|
1800
|
1928
|
|
Балансовая прибыль
|
240
|
294
|
|
Среднегодовая стоимость основных
производственных средств
|
1420
|
1510
|
|
Среднегодовая стоимость
материальных оборотных средств
|
258
|
304
|
Определите:
1.Показатели рентабельности
продукции и производства;
2.Изменение рентабельности общее
и в том числе вследствие изменения:
А) рентабельности продукции;
Б) фондоемкости продукции;
В) коэффициента закрепления.
Сделайте выводы.
Решение:
Найдем показатель рентабельности
продукции:
Rб = Rr/(1/H+1/K),
Где Rr =
0,133. Н = В/S = 1,3. К
= РП/Sоб.ср. = 6,98.
Исходя из формулы, Rб = 0,133/(0,769 + 0,143) = 0,145.
Rо = Rr/(1/H+1/K),
Где Rr =
0,152. Н = В/S = 1,276.
К = РП/Sоб.ср. = 6,342.
Исходя из формулы, R0 = 0,152/(0,783+ 0,157) = 0,161.
Найдем показатель рентабельности
производства по формуле:
Rпр. = Rо - Rб =
0,161 – 0,145 = 0,016.
Найдем изменение рентабельности
общее:
Rпр.б. = 0,016+0,145 = 0,161.
Rпр.о. = 0,016 + 0,161 = 0,177.
∆R = 0,016.
Найдем изменение
рентабельности вследствие изменения
рентабельности продукции:
∆R1 = 0.161/(0,769 + 0,143) – 0,145 /(0,769
+ 0,143) = 0.171 – 0.154 = 0,017.
Найдем изменение
рентабельности вследствие изменения фондоемкости
продукции:
∆R2 = 0.161/ (0,783
+0,143) - 0.161/(0,769 + 0,143) = 0,173 – 0,176 =
-0,003.
Найдем изменение
рентабельности вследствие изменения коэффициента
закрепления:
∆R3 = 0.161/(0,783+ 0,157) - 0.161(0,783+0,143)
= 0,171 – 0,149 = 0,022.
Найдем суммарную величину влияния
трех факторов:
∆R = ∆R1+ ∆R2+ ∆R3=0,017 – 0,003 + 0,022 = 0,036.
Таким образом, изменение данных
трех факторов в целом оказывает на изменение рентабельности положительное
влияние. Однако в частности изменение фондоемкости продукции отрицательно
влияет на изменение рентабельности.
Список использованной
литературы
1. Гусаров
В.М. Статистика: Учебное пособие для вузов. – М: ЮНИТИ-ДАНА, 2001.
2. Салин
В.Н., Шпаковская Е.П. Социально-экономическая статистика: учебник. – М.: Юристъ,
2001.
3. Сборник
задач по теории статистики: Учебное пособие/Под ред. В.В. Глинского. – изд.3-е.
– М: ИНФРА-М; Новосибирск: Сибирское соглашение, 2002.
4. Статистика:
Учебное пособие/Харченко Л.П., Долженкова В.Г.. – изд 2-е. – М: ИНФРА-М, 2001.
5. Теория
статистики: Учебник/Под ред. Р.А. Шмойловой. – М.: Финансы и статистика, 2000.