1. Постановка экономической задачи

Продукцией городского молочного завода являются молоко, кефир и сметана. На производство 1 т. Молока, кефира и сметаны требуется соответственно 1,01; 1,01 и 9,45 т. Молока. При этом затраты рабочего времени при разливе 1т. Молока и кефира составляют 0,18 и 0,19 машиночаса. На расфасовке 1 т. Сметаны заняты специальные автоматы в течении 3,25 ч. Всего для производства цельномолочной продукции завод может использовать 136 т. Молока. Основное оборудование может быть занято в течении 21,4 машиночасов, а автоматы по расфасовке сметаны – в течении 16,25 ч. Прибыль от реализации 1 т. Молока, кефира и сметаны соответственно равна 30,22 и 136 руб. Завод должен ежедневно производить не менее 100 т. молока.

Требуется определить  объемы выпуска молочной продукции, позволяющие получить наибольшую прибыль. К чему приведет  задание по выпуску  кефира в объеме не менее 10 т.

2. Экономико-математическая модель

Обозначим через x₁ , x₂  и x₃ объемы производства соответствующего вида продукции (Молока, кефира и сметаны).

Найти наибольшее значение функции 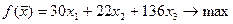 при ограничениях:

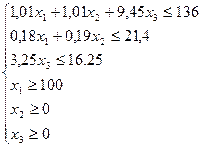
3. Описание компьютерной информационной технологии получения оптимального решения

Решение данной задачи проведено средствами Excel в 3 этапа.

На I этапе создан рабочий лист Excel:

Ø    определены изменяемые ячейки (B3:D3),

Ø    целевая ячейка (E3),

Ø    ячейки для задания ограничений (B10:B12; D10:D12).

Для создания целевой ячейки и ячеек функций использовалась стандартная функция Excel – СУММПРОИЗВ.

Для наглядности создание целевой ячейки представлено в Рис.1.

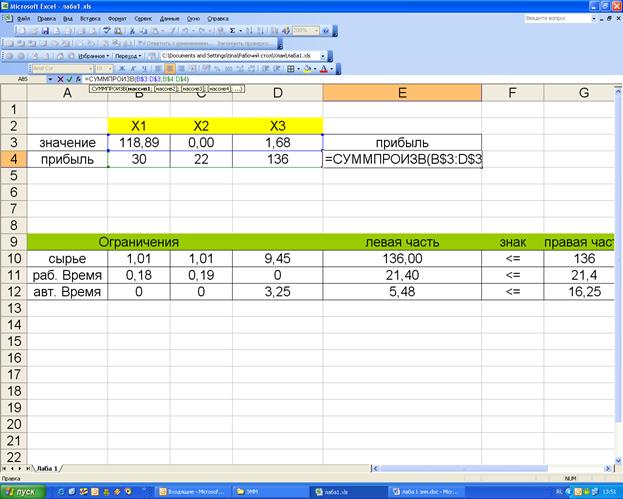
Рис. 1. Целевая ячейка

На II этапе вызываем программу оптимизации и оформляем окно диалога «Поиск решения».

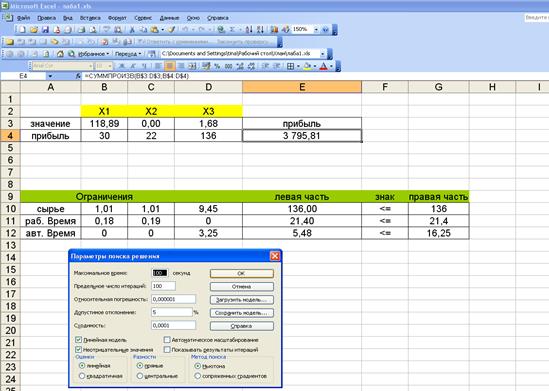
Рис. 2. Параметры поиска решения

В режиме параметры окна диалога «Поиск решения» мы определяем тип задачи – линейная (Рис.2.).

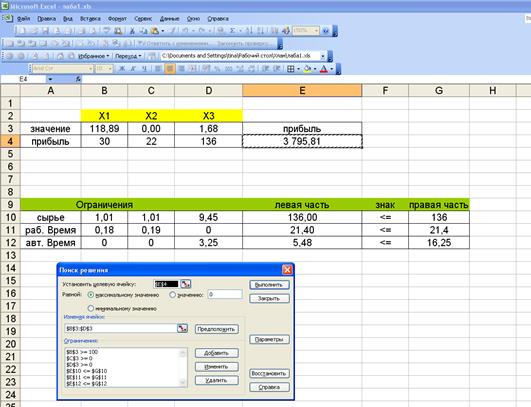
Рис. 3. Результаты поиска решения

На III этапе оптимизируем результаты с помощью окна «Результаты поиска решения» Рис. 3.

Рис.4. Результаты поиска решения, при введение дополнительного ограничения по выпуску кефира.[1]

4. Предложения (рекомендации) лицу, ответственному за принятие решений, по оптимальному управленческому поведению

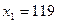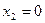
1)    Получено оптимальное решение при заданных ограничениях: , . Максимальное значение целевой функции или иначе максимальная прибыль составит 3 796 руб.

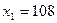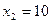
2)    При введение дополнительных условий (, т.е. кефира должно выпускаться не менее 10 т.), получим следующие оптимальные значения искомых параметров (рис. 4) , 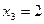. Максимальное значение целевой функции или иначе максимальная прибыль составит 3 707 руб. Т.е. при обязательном выпуске 10 т. кефира прибыль уменьшиться на 89 руб.