ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

ФИЛИАЛ В Г.УФЕ

КАФЕДРА МАТЕМАТИКИ И ИНФОРМАТИКИ

О Т Ч Е Т

о результатах выполнения

лабораторной работы № 1

по дисциплине

Экономико-математические методы и прикладные модели

Вариант № _4_

Выполнил: _3курс, ФиК, 3 группа _

Курс, поток, специальность, группа

05ФФД12454

______________________________

                                                                                                                                          № зачетной книжки

Елизарьева Р.С.

______________________________

                                                                                                                                           Ф.И.О. 

                                                                                 Проверил:          Фархиева С.А.

                                                                                                                        ________________________

                                                                                                                                                  Ф.И.О.

Уфа, 2007 г.

Задача 1.4

Стандартом предусмотрено, что октановое число автомобильного бензина А-76 должно быть не ниже 76, а содержание серы в нем – не более 0,3%. Для изготовления такого бензина на заводе используется смесь из четырех компонентов. Данные о ресурсах смешивания  компонентов, их себестоимость и их октановом числе приведены в таблице.

Требуется определить, сколько тонн каждого компонента следует использовать для получения 1000 т автомобильного бензина А-76, чтобы себестоимость была минимальной.

Экономико-математическая модель

Обозначим х1, х2, х3, х4 – количество компонентов автомобильного бензина.

Целевая функция – это выражение, которое необходимо минимизировать:

F(x)=40x1+45x2+60x3+70x4 -> min

68x1+72x2+80x3+90x4>=76*1000

0.35x1+0.35x2+0.3x3+0.2x4<=0.3*1000

х1<=700

x2<=600

x3<=500

x4<=300

x1, x2, x3, x4>=0

1.      В программе Microsoft Excel создадим текстовую форму – таблицу для ввода условий. Вводим исходные данные задачи в созданную таблицу, представленную на рис. 1.

Рис 1. Исходные данные.

2.      Вводим зависимость для целевой функции с помощью «Мастер  функций»

·         в окне «Категория»  выбираем категорию Математические;

·         в окне Функции на СУММПРОИЗВ;

·         на экране появляется диалоговое окно  СУММПРОИЗВ;

·         в строку «Массив 1» вводим  В3:Е3;

·         в строку «Массив 2» вводим В4:Е4=>кнопка «Ок». Рис. 2

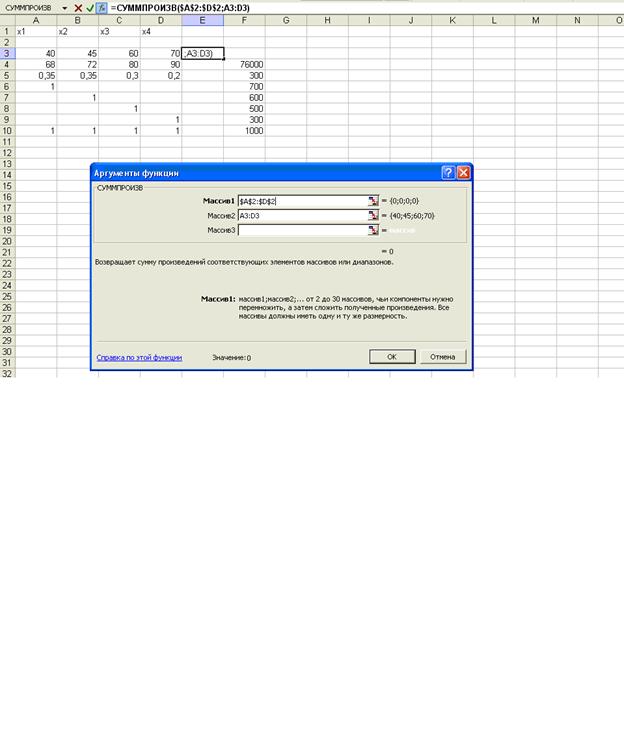
Рис. 2.

3.      Вводим зависимости для ограничений:

·         содержание ячейки Е3 скопировать в ячейки Е4-Е10

4.      Выбираем с строке МЕНЮ имя СЕРВИС => ПОИСК РЕШЕНИЯ. Появляется диалоговое окно ПОИСК РЕШЕНИЯ

·         Назначить целевую функцию: курсор в строку УСТАНОВИТЬ ЦЕЛЕВУЮ ЯЧЕЙКУ;

·         Вводим адрес ячейки Е3;

·         Вводим направление целевой функции – МИНИМАЛЬНОМУ ЗНАЧЕНИЮ;

·         Курсор в строку изменяя ячейки ;

·         Вводим адрес В3:Е3;

·         Вводим ограничения: нажимаем на ДОБАВИТЬ. Появляется диалоговое окно ДОБАВЛЕНИЕ ОГРАНИЧЕНИЯ;

·         В строке ССЫЛКА НА ЯЧЕЙКУ вводим адрес Е10;

·         Вводим знак «=»;

·         В строке ОГРАНИЧЕНИЕ  адрес F10 -> ДОБАВИТЬ;

·         В строке ССЫЛКА НА ЯЧЕЙКУ адрес E4;

·         Вводим знак « >=»;

·         В строке ОГРАНИЧЕНИЕ  адрес F4-> ДОБАВИТЬ ;

·         В строке ССЫЛКА НА ЯЧЕЙКУ адрес E5;

·         Вводим знак «<=»;

·         В строке ОГРАНИЧЕНИЕ  адрес F5-> ДОБАВИТЬ ;

·         В строке ССЫЛКА НА ЯЧЕЙКУ адрес E6;

·         Вводим знак «<=» ;

·         В строке ОГРАНИЧЕНИЕ  адрес F6 -> ДОБАВИТЬ;

·         В строке ССЫЛКА НА ЯЧЕЙКУ адрес E7;

·         Вводим знак «<=» ;

·         В строке ОГРАНИЧЕНИЕ  адрес F7 -> ДОБАВИТЬ;

·         В строке ССЫЛКА НА ЯЧЕЙКУ адрес E8;

·         Вводим знак «<=» ;

·         В строке ОГРАНИЧЕНИЕ  адрес F8 -> ДОБАВИТЬ;

·         В строке ССЫЛКА НА ЯЧЕЙКУ адрес E9;

·         Вводим знак «<=» ;

·         В строке ОГРАНИЧЕНИЕ  адрес F9 -> ДОБАВИТЬ;

·         Нажимаем «Ок»

5.      На экране появилось диалоговое окно ПОИСК РЕШЕНИЯ с введенными условиями. Рис. 3.

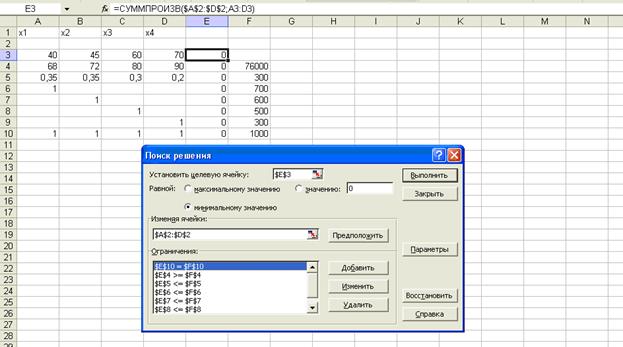
Рис. 3

6.      Введем ПАРАМЕТРЫ:

·         В диалоговом окне нажимаем ПАРАМЕТРЫ, рис.4;

·         Нажимаем «Ок».

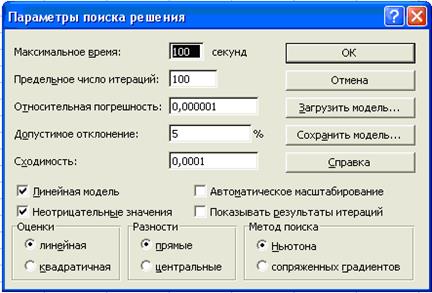
Рис. 4

7.      Нажимаем ВЫПОЛНИТЬ. Появляется РЕЗУЛЬТАТЫ ПОИСКА РЕШЕНИЯ, выбираем в поле ТИП ОТЧЕТА – РЕЗУЛЬТАТЫ, рис. 5. Нажимаем «Ок».

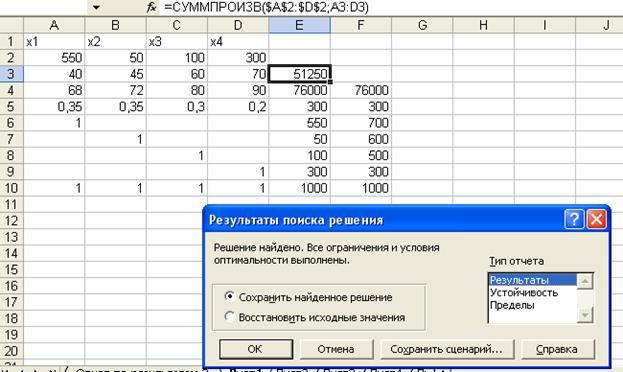
Рис. 5

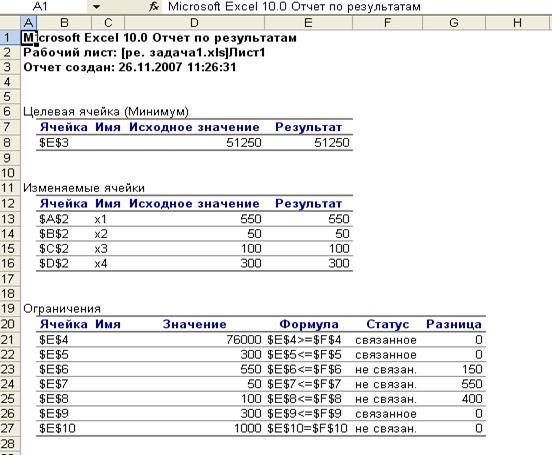
Ответ: оптимальное решение  в данной ситуации  определяется вектором  объемов смешиваемых компонент (550 т; 50т; 100; 300т), оценка затрат – 51250 ден.ед.

Задача2

Компания, занимающаяся ремонтом автомобильных дорог, в следующем месяце будет проводить ремонтные работы на пяти участках автодорог. Песок на участки ремонтных дорог может доставляться из трех карьеров, месячные объемы предложений по карьерам известны. Из планов производства  ремонтных работ известны месячные объемы потребностей по участкам работ. Имеются экономические оценки транспортных затрат (в у.е) на  перевозку 1 тонны песку с карьеров на ремонтные участки.

Требуется:

1.      Предположить план перевозок песка на участки ремонта автодорог, который обеспечивает минимальные совокупные транспортные издержки.

2.      Определить, что произойдет с  оптимальным планом, если изменятся условия перевозок: а) появится запрет на перевозки от первого карьера до второго участка работ; б) по этой коммуникации будет ограничен объем перевозок 3 тоннами.

Матрица планирования

1. Создаем  форму для решения задачи.

• Создаем матрицу перевозок , вводим в блок ячеек В3:F5 «1»

2. Вводим исходных данных.
3. Вводим граничные условия:

• Поместить курсор в ячейку А3;
• Выбрать знак ∑;
• Выделить ячейки В3:F3;
• Нажать ENTER;

Аналогично для ячеек А4, А5.

·           Поместить курсор в ячейку В6;

·           Выбрать знак ∑, при этом автоматически выделяется весь столбец В3:В5;

·           Нажать ENTER;

Аналогично для ячеек C6-F6. рис. 1.;

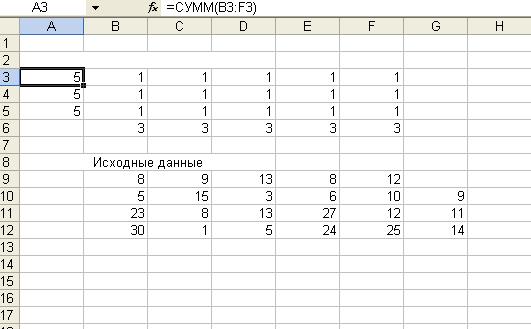
Рис . 1.

4. Назначим целевую функцию.

·         Поместить курсор В14;

·         запустить Мастер функций;

·         в окне Категория выбрать Математические;

·         в окне Функции выбрать  СУММПРОИЗВ;

·         нажать кнопку Ок;

·         в окне СУММПРОИЗВ указать адреса массивов, элементы которых обрабатываются этой функцией;

·         в поле Массив1 указать адреса В10:F12;

·         в поле Массив2 указать адреса B3:F5;

·         нажать кнопку Ок. рис. 2.

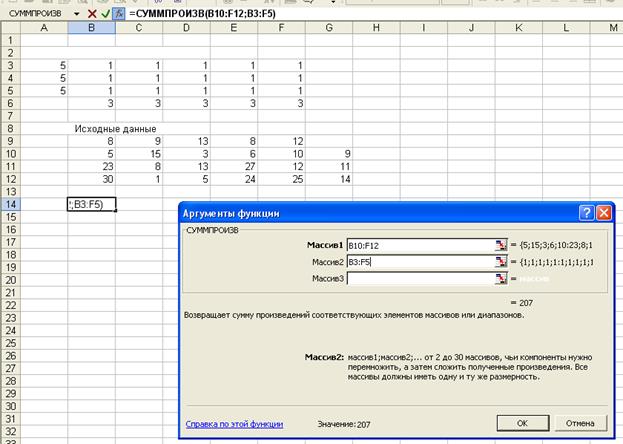
Рис. 2.

5. Ввод зависимости для математической модели.

·        Выбрать Сервис => Поиск решения;

·        В поле Установить целевую ячейку, вводим адрес $B$14;

·        Установим направление изменения целевой функции, равное Минимальному значению;

·        Вводим адреса изменяемых ячеек В3:F5;

6. Ввод ограничений задачи.

·        Выбрать Добавить ограничения;

·        В поле Ссылка на ячейку вводим адреса $A$3:$A$5;

·        Установим знак “<=”;

·        В поле Ограничение установить адреса $G$10:$G$12;

·        Нажать Добавить;

·        В поле Ссылка на ячейку вводим адреса $B$6:$F$6;

·        Установим знак  “=”;

·        В поле Ограничение установить адреса $B$9:$F$9;

·        Нажать Ок; рис. 3.

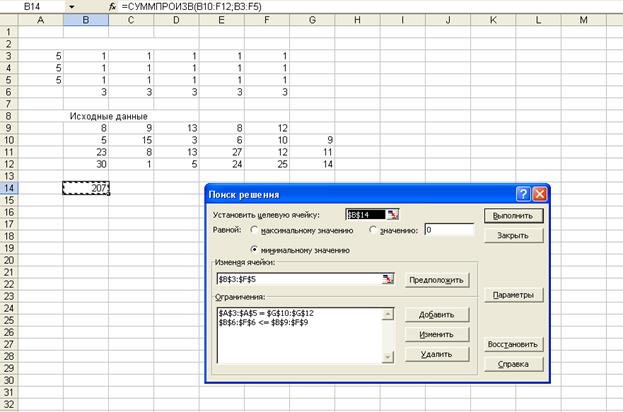
Рис. 3.

7. Ввод параметров.

·         Щелкнуть по кнопке Параметры;

·         Установим флажок Линейная модель;

·         Установим флажок Неотрицательные значения;

·         Нажимаем Ок. Рис. 4

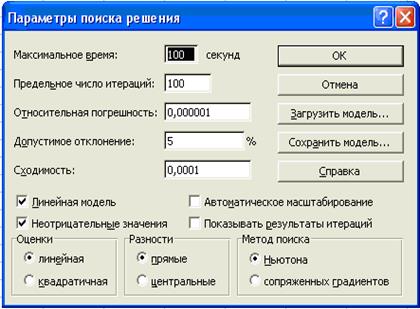
Рис. 4

После этого произойдет переход в поле Поиск решения;

·         Нажать кнопку Выполнить. Рис. 5

В результате получим оптимальный план перевозок:

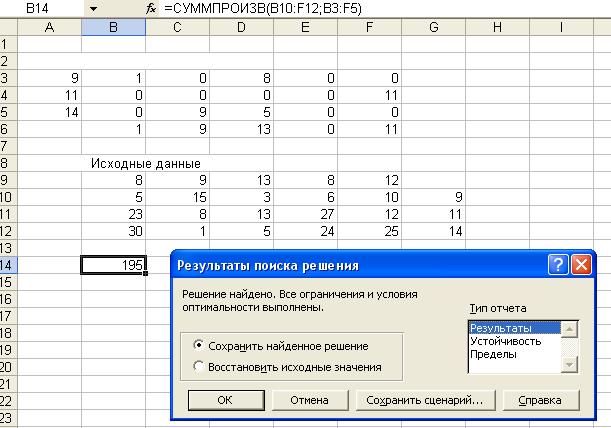
Рис. 5

Вывод: Минимум затрат на перевозку песка на участки ремонта  автодорог, равный 195 условных единиц, будет обеспечен при следующем плане

·         от первого карьера  до первого участка работ в объеме 1 единицы  и до третьего  в объеме  8 условных единиц;

·         от второго карьера до пятого  участка работ в объеме 11 условных единиц;

·         от третьего карьера до второго участка работ в объеме 9 условных единиц и до третьего в объеме 5 условных единиц.

Задача 3

Необходимо решить транспортную задачу: минимизировать расходы на доставку продукции заказчикам со складов фирмы, учитывая следующие затраты на доставку  одной единицы продукции, объем заказа и количество продукции, хранящейся на каждом складе.

Таблица тарифов на перевозку продукции и объемов запасов на складе и заказов:

1.   Создаем  форму для решения задачи.

• Создаем матрицу перевозок , вводим в блок ячеек В2:F4 «1»

2.      Вводим исходных данных.

3.      Вводим граничные условия:

• Поместить курсор в ячейку А2;
• Выбрать знак ∑;
• Выделить ячейки В2:F2;
• Нажать ENTER;

Аналогично для ячеек А3, А4.

·           Поместить курсор в ячейку В5;

·           Выбрать знак ∑, при этом автоматически выделяется весь столбец В2:В4;

·           Нажать ENTER;

Аналогично для ячеек C5-F5. рис. 1.;

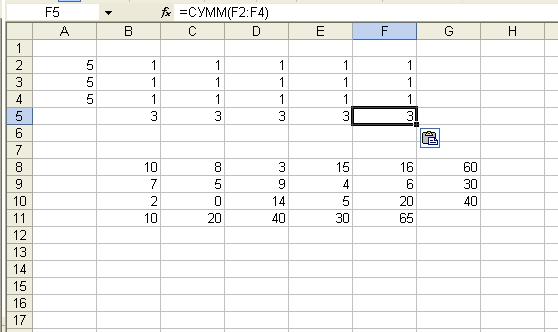
Рис . 1.

4.   Назначим целевую функцию.

·         Поместить курсор В14;

·         запустить Мастер функций;

·         в окне Категория выбрать Математические;

·         в окне Функции выбрать  СУММПРОИЗВ;

·         нажать кнопку Ок;

·         в окне СУММПРОИЗВ указать адреса массивов, элементы которых обрабатываются этой функцией;

·         в поле Массив1 указать адреса В8:F10;

·         в поле Массив2 указать адреса B2:F4;

·         нажать кнопку Ок. рис. 2.

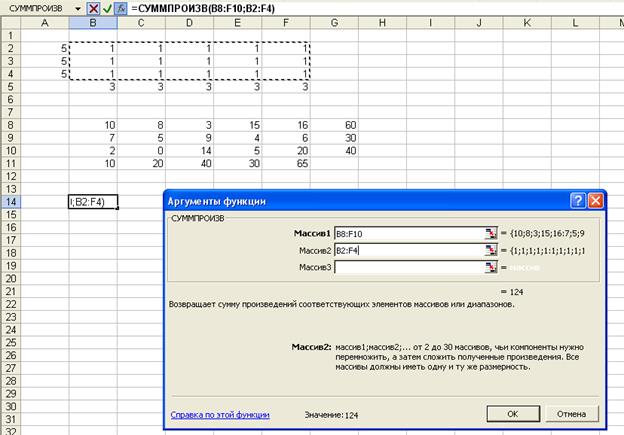
Рис. 2.

5        Ввод зависимости для математической модели.

·        Выбрать Сервис => Поиск решения;

·        В поле Установить целевую ячейку, вводим адрес $B$14;

·        Установим направление изменения целевой функции, равное Минимальному значению;

·        Вводим адреса изменяемых ячеек В2:F4;

·                                Ввод ограничений задачи.

·        Выбрать Добавить ограничения;

·        В поле Ссылка на ячейку вводим адреса $A$2:$A$4;

·        Установим знак “=”;

·        В поле Ограничение установить адреса $G$8:$G$10;

·        Нажать Добавить;

·        В поле Ссылка на ячейку вводим адреса $B$5:$F$5;

·        Установим знак  “<=”;

·        В поле Ограничение установить адреса $B$11:$F$11;

·        Нажать Ок; рис. 3.

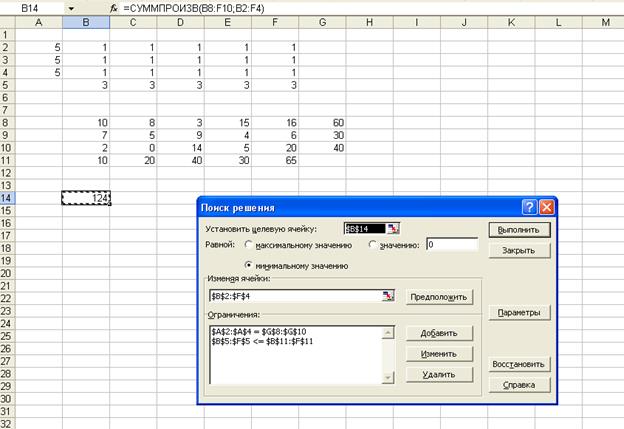
Рис. 3.

·                                Ввод параметров.

·         Щелкнуть по кнопке Параметры;

·                     Установим флажок Линейная модель;

·                     Установим флажок Неотрицательные значения;

·                     Нажимаем Ок. Рис. 4

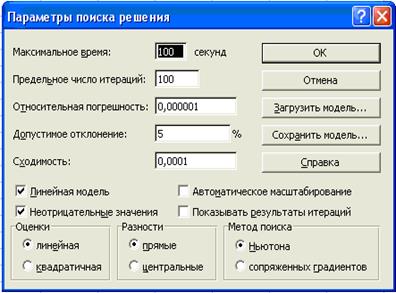
Рис. 4

После этого произойдет переход в поле Поиск решения;

·        Нажать кнопку Выполнить. Рис. 5

В результате получим оптимальный план перевозок:

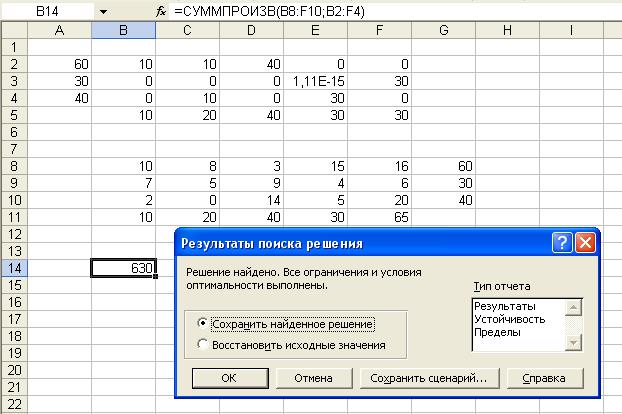
Рис. 5

Вывод: Минимум расходов на доставку  продукции заказчикам со складов  фирмы, равный 630 условных единиц, будет обеспечен при следующем  плане

·        От склада Пролетарская до магазина ВДНХ в объеме 10 единиц, до магазина Юго-Западная в объеме 10 единиц и до магазина Фили в объеме 40 единиц;

·        От склада Митино до магазина Арбатская в объеме 1,11Е-15=0 и до магазина Сокольники в объеме 30 единиц;

·            От склада Строгино до магазина Юго-западная в объеме10 единиц и до магазина Арбатская в объеме 30 единиц.

Задача 4

Необходимо решить транспортную задачу: минимизировать расходы на доставку продукции заказчикам со складов фирмы, учитывая следующие затраты на доставку  одной единицы продукции, объем заказа и количество продукции, хранящейся на каждом складе.

Таблица тарифов на перевозку продукции и объемов запасов на складе и заказов:

1.   Создаем  форму для решения задачи.

• Создаем матрицу перевозок , вводим в блок ячеек В2:Е4 «1»

2.      Вводим исходных данных.

3.      Вводим граничные условия:

• Поместить курсор в ячейку А2;
• Выбрать знак ∑;
• Выделить ячейки В2:Е2;
• Нажать ENTER;

Аналогично для ячеек А3, А4.

·           Поместить курсор в ячейку В5;

·           Выбрать знак ∑, при этом автоматически выделяется весь столбец В2:В4;

·           Нажать ENTER;

Аналогично для ячеек C5-Е5. рис. 1.;

Рис. 1

4.   Назначим целевую функцию.

·        Поместить курсор В13;

·              запустить Мастер функций;

·              в окне Категория выбрать Математические;

·              в окне Функции выбрать  СУММПРОИЗВ;

·              нажать кнопку Ок;

·              в окне СУММПРОИЗВ указать адреса массивов, элементы которых обрабатываются этой функцией;

·              в поле Массив1 указать адреса В8:Е10;

·              в поле Массив2 указать адреса B2:Е4;

·              нажать кнопку Ок. рис. 2.

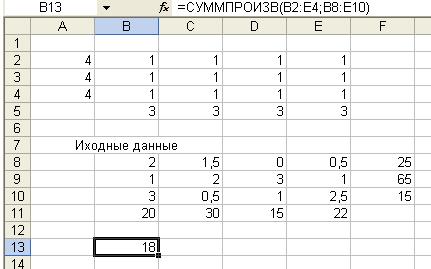
Рис. 2.

5        Ввод зависимости для математической модели.

·        Выбрать Сервис => Поиск решения;

·        В поле Установить целевую ячейку, вводим адрес $B$13;

·        Установим направление изменения целевой функции, равное Минимальному значению;

·        Вводим адреса изменяемых ячеек В2:Е4;

·                                Ввод ограничений задачи.

·        Выбрать Добавить ограничения;

·        В поле Ссылка на ячейку вводим адреса $A$2:$A$4;

·        Установим знак “<=”;

·        В поле Ограничение установить адреса $F$8:$F$10;

·        Нажать Добавить;

·        В поле Ссылка на ячейку вводим адреса $B$5:$Е$5;

·        Установим знак  “=”;

·        В поле Ограничение установить адреса $B$11:$Е$11;

·        Нажать Ок; рис. 3.

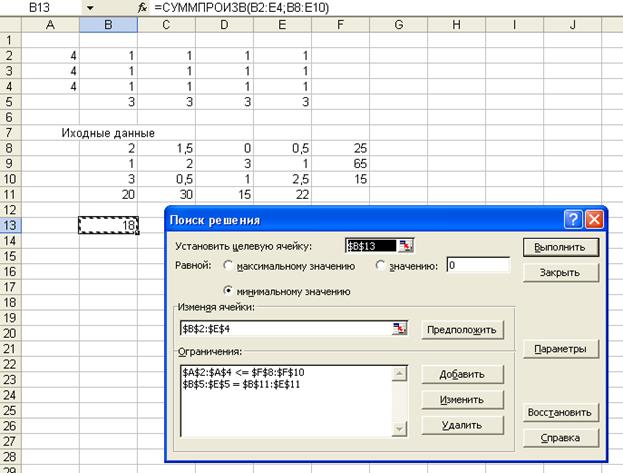
Рис. 3.

·                                      Ввод параметров.

·         Щелкнуть по кнопке Параметры;

·                     Установим флажок Линейная модель;

·                     Установим флажок Неотрицательные значения;

·                     Нажимаем Ок. Рис. 4

Рис. 4

После этого произойдет переход в поле Поиск решения;

·        Нажать кнопку Выполнить. Рис. 5

В результате получим оптимальный план перевозок:

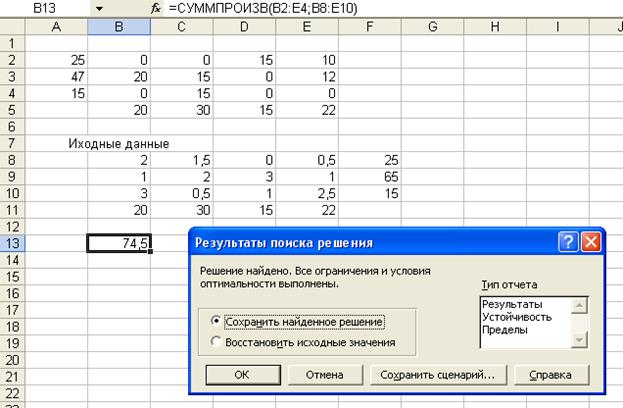
Вывод: Минимум расходов на доставку  продукции заказчикам со складов  фирмы, равный 74,5 условных единиц, будет обеспечен при следующем  плане

·        Со склада Рижская  до заказчика «Детский  мир» в объеме 15 единиц и до заказчика «Книги» в объеме 10 единиц;

·        Со склада Фили до заказчика  Типография №2 в объеме 20 единиц , до заказчика «Школьник»  15 единиц и до «Книги» 12 единиц;

·        Со склада Выхино до заказчика «Школьник» в объеме 15 единиц.