Содержание

Задача 1. 3

Задача 2. 6

Задача 3. 9

Список литературы.. 11

Задача 1

          Основываясь на данных о цене товара и объёме проданных товаров, необходимо:

1.     Проанализировать существующую зависимость между объёмом продажи и ценой;

2.     Определить коэффициент эластичности между ценой и объёмом;

3.     Определить тесноту связи между ценой и объёмом продажи.

Решение:

1.     Построим график зависимости между объёмом продажи и ценой.

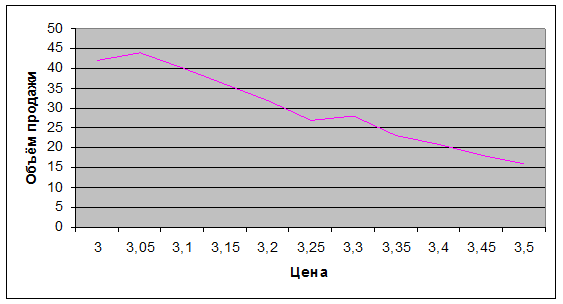
          Исходя из рисунка, мы видим, что для описания зависимости может быть использовано уравнение прямой у = а0 + а1*х. Для расчёта значений а0 и а1 составляем вспомогательную таблицу:

n	Цена (х)	Объём продажи (у)	х*у	х²	у²
1	3	42	126	9	1764
2	3,05	44	134,2	9,3025	1936
3	3,1	40	124	9,61	1600
4	3,15	36	113,4	9,9225	1296
5	3,2	32	102,4	10,24	1024
6	3,25	27	87,75	10,5625	729
7	3,3	28	92,4	10,89	784
8	3,35	23	77,05	11,2225	529
9	3,4	21	71,4	11,56	441
10	3,45	18	62,1	11,9025	324
11	3,5	16	56	12,25	256
Итого	35,75	327	1046,7	116,4625	10683
Среднее	3,25	29,73	-	-	-

          Значение коэффициента а1 определяется по формуле: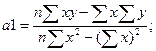

Используя данные таблицы, получим: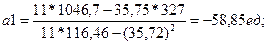

          Это число показывает теоретическую величину падения объёма продаж при увеличении цены на единицу стоимости.

          Коэффициент а0 для средних значений рассчитаем по формуле: а0 = у – а1*х = 29,73 + 58,85 * 3,25 = 220,99 ед.

          Это число показывает теоретически возможный объём продаж при минимальной цене, тогда теоретическое уравнение зависимости цены от объёма примет вид:

          У(х) = 220,99 – 58,85 * х;

          Расчёт значений сведём в таблицу:

n	Цена (х)	Объём продажи (у)	У(х)
1	3	42	44,44
2	3,05	44	41,4975
3	3,1	40	38,555
4	3,15	36	35,6125
5	3,2	32	32,67
6	3,25	27	29,7275
7	3,3	28	26,785
8	3,35	23	23,8425
9	3,4	21	20,9
10	3,45	18	17,9575
11	3,5	16	15,015
Итого	35,75	327	327
Среднее	3,25	29,73

 

2.     Коэффициент эластичности рассчитывается по формуле: Кэ = а1 * х(ср) / у(ср); Используя данные расчётов в предыдущем пункте определим значение коэффициента эластичности спроса по цене: Кэ = -58,85 * 3,25 / 29,73 = -6,4; это число показывает процент изменения объёма продаж при изменении цены на 1%, т.к. Кэ < 1, то спрос неэластичный.

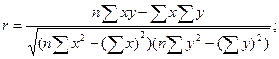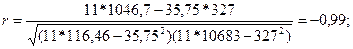3.     Теснота связи рассчитывается по формуле:  подставляя наши данные получим  Т.к. полученное значение меньше 0, то это значит, что связь обратная; т.к. по абсолютному значению близка к 1, то это значит что связь стремится к функциональной.

Вывод: Фирме не стоит прибегать к политике высоких цен, наиболее разумно будет получить дополнительные прибыли за счёт увеличения объёма продаж.

Задача 2

          Проанализировать затраты на производство обращение товара:

1.     Разделить суммарные издержки, используя метод «максимальной и минимальной точки»;

2.     Разделить суммарные издержки с помощью метода наименьших квадратов;

3.     Составить математическую модель валовых издержек производства и обращения товара;

Решение:

          1. Из всей совокупности данных выберем два периода с наибольшим и наименьшим объёмом производства: мах – ноябрь – 280 шт.; min – июнь – 160. Составим вспомогательную таблицу.

Показатель	Объём производства	Разность (мах – min)
мах	min
Уровень производства Q, (Q%)	280 100%	160 57,14%	120 42,86%
Расходы производства, тыс. руб. (ТС)	2615	2370	245

          Определим ставку переменных издержек ( VC’ – средние переменные расходы в себестоимости единицы продукции) по следующей формуле:

VC’ = (ΔTC * 100 / ΔQ%) / Qмах = 245 * 100 / 42,86% / 280 = 2,04 тыс. руб./шт.;

          Общая сумма постоянных издержек – FC:

FC = TCmax – VC’ * Qmax = 2615 – 2,04 * 280 = 2043 тыс. руб.;

          Таким образом, получим формулу валовых издержек производства:

ТС = FC + VC’ * Q = 2043 + 2,04 * Q,

          Где Q – объём производства;

2. Метод наименьших квадратов позволяет наиболее точно определить состав общих затрат и содержание в них переменной и постоянной составляющей. Согласно этому методу рассчитываем коэффициенты а и b, в уравнении прямой у = а + б * х; где у – общие издержки обращения; а – уровень постоянных издержек; b – ставка переменных издержек на единицу товара; х – объём реализации. Ставка переменных издержек рассчитывается по формуле: 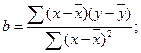Для расчёта составим вспомогательную таблицу:

Месяц	Объём реализации (х)	х-х(ср)	Суммарные издержки (у)	у-у(ср)	(х-х(ср))²	(х-х(ср)) * (у-у(ср))
1	190	-37,5	1155	-47,92	1406,25	1796,88
2	160	-67,5	1135	-67,92	4556,25	4584,38
3	180	-47,5	1145	-57,92	2256,25	2751,04
4	230	2,5	1190	-12,92	6,25	-32,29
5	180	-47,5	1140	-62,92	2256,25	2988,54
6	240	12,5	1200	-2,92	156,25	-36,46
7	260	32,5	1300	97,08	1056,25	3155,21
8	250	22,5	1225	22,08	506,25	496,87
9	270	42,5	1300	97,08	1806,25	4126,04
10	230	2,5	1195	-7,92	6,25	-19,79
11	280	52,5	1230	27,08	2756,25	1421,88
12	260	32,5	1220	17,08	1056,25	555,21
Итого	2730		14435		17825	21787,50
Среднее	227,5		1202,92

          Используя формулу и полученные значения, вычислим ставку переменных издержек (VC’) b = (2730 + 14435) / 17825 = 0,96 тыс. руб./ шт.

          Тогда переменные издержки  на среднесуточный объём продаж VC = VC’ * Q = 227,5 * 0,96 = 219,07 тыс. руб.

          Постоянные издержки FC = TC – VC = 1202.92 – 219,07 = 983,85 тыс. руб.;

          Таким образом, валовые издержки обращения могут быть рассчитаны по формуле: ТС = 983,85 + 0.96 *  Q;

          Используя результаты предыдущей задачи, определяем, что постоянные издержки на производство и реализацию равны 2043 + 983,85 = 3026,85 тыс. руб.;

          А удельные переменные издержки 2,04 + 0,96 = 3 тыс. руб./ шт.

          Таким образом, математическая модель валовых издержек производства и обращения товара будет выглядеть: ТС = 3026,85 + 0,96 * Q;

Задача 3

          Используя результаты, полученные в задачах 1 и 2 необходимо определить:

1.     Оптимальный уровень цены с учётом достижения максимальной прибыли, предварительно разработав экономико-математическую модель задачи;

2.     Объём производства и продажи, обеспечивающий прибыль равную 50 тыс. руб. в день;

3.     Оптимальный уровень цены, обеспечивающий уровень прибыли, равный 50 тыс. руб. в день при уровне производства и реализации равном 3000 и более штук.

Решение:

1.     Используем результаты предыдущих задач:

Зависимость объёма реализации от цены: Q = 221 – 59 * Ц (задача 1);

Постоянные издержки – 3027 тыс. руб;

Удельные переменные издержки – 3 тыс. руб./ шт.;

Разработаем экономико-математическую модель (формулу прибыли):

П = Q * Ц – VC’ * Q – FC > мах

          Подставим в формулу соответствующие значения Q и VC’. Тогда формула преобразится:

П = 221 * Ц – 59 * Ц² - 663 + 177 * Ц - FC = 398Ц – 59Ц² - 3027;

          Для расчёта оптимальной цены возьмём производную этой формулы и приравняем к 0:

398 – 118Ц = 0;

          Тогда оптимальная цена Ц = 398 / 118 = 3,37 тыс. руб.;

2.     Предположим, что необходимо определить количество товара, который нужно продать для получения целевой прибыли 50 тыс. руб. в день. Для этого используем формулу:

 П = Q * Ц – VC’ * Q – FC = 50000

          Тогда Q = (3027 + 50) / (Ц – VC’) = 3077 / (Ц – 3);

          Расчет для определения минимального объёма сведём в таблицу:

Цена единицы товара	Ц - 3	Объём реализации
3,1	0,1	30770
3,2	0,2	15385
3,3	0,3	10257
3,4	0,4	7693
3,5	0,5	6154
3,6	0,6	5128

         

          Таким образом, для получения прибыли 50 тыс. руб. в день, при оптимальной цене 3,4 тыс. руб. необходимо продать 7693 шт.

3.     Для нахождения оптимальной цены при уровне производства 3000 и более штук в день используем формулу:

П = Q * Ц – VC’ * Q – FC = 50000

          Отсюда Ц = (50 + FC + VC’*Q) / Q = (3077 + 3Q) / Q;

          Расчет сведём в таблицу:

Q	3000	3500	5000	10000	20000	30000
Ц	4,026	3,879	3,615	3,308	3,154	3,103

         

Таким образом, мы сталкиваемся с действием «эффекта масштаба», т.е. чем больше будут объёмы производства фирмы, тем ниже будет цена.

Список литературы

1.     Башарин Г.П. Эконометрика. – М.: «Инфра-М», 1997.

2.     Дихль Е. Практический маркетинг, - М.: «Юнити», 1999г.

3.     Ковалёв В.В. Курс финансовых вычислений. – М.: «Финансы и статистика», 1999.

4.     Котлер Ф. Основы маркетинга, - М.: «Финансы и статистика», 1996г.

5.     Кочович Е. Финансовая математика. – М.: «Финансы и статистика», 1994.

6.     Малыхин В.И. Финансовая математика. – М.: «Юнити», 1999.