4) Построить точечный прогноз на 4 шага вперед, т.е. на 1 год.

5) Отразить на графике фактические, расчетные и прогнозные данные.

Таблица №1  -  Исходные данные.

Решение:

Исходные данные:

1. Построение адаптивной мультипликативной модели Хольта-Уинтерса

Линейная модель имеет вид: Yp = a(0) + b(0)*t

Согласно методу наименьших квадратов:

 ;  ;

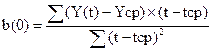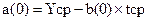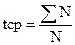
Все расчеты произведем в таблице

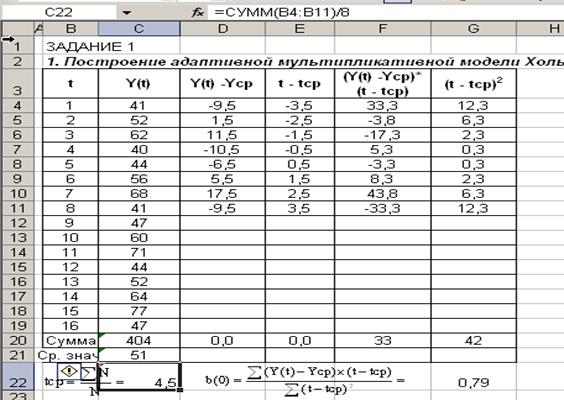
Уравнение с учетом найденных коэффициентов имеет вид: Yp = 49,6 + 0,4*t. Из этого уравнения находим расчетные значения Yp(t) и сопоставляем их с фактическими значениями:

Такое сопоставление позволяет оценить приближенные значения коэффициентов сезонности кварталов F(-3), F(-2), F(-1) и F(0) Эти значения необходимы для расчета коэффициентов сезонности первого года F(1), F(2), F(3), F(4) и других параметров модели Хольта –Уинтерса.

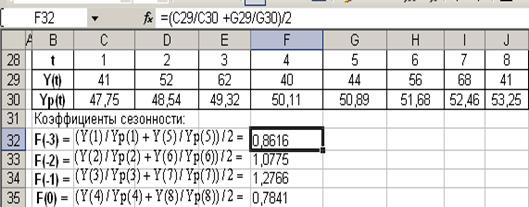
Рассчитаем значения Yp(t), a(t), b(t), F(T) для t=1 значения параметров сглаживания α1=0,3, α2=0,6, α3=0,3.

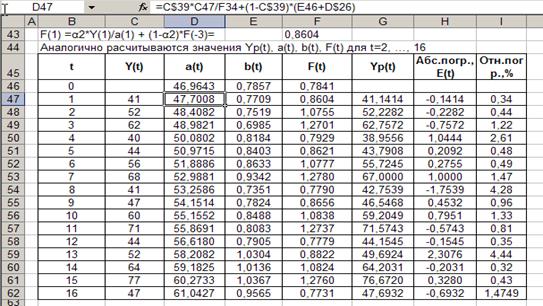
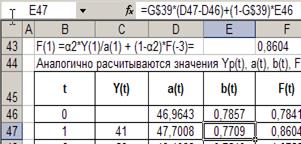
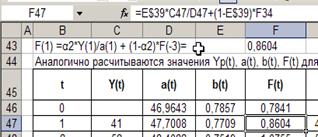
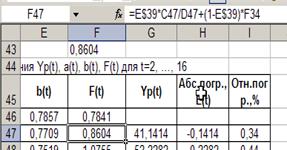
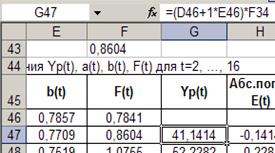
2. Проверка качества модели

Промежуточные значения для оценки адекватности модели

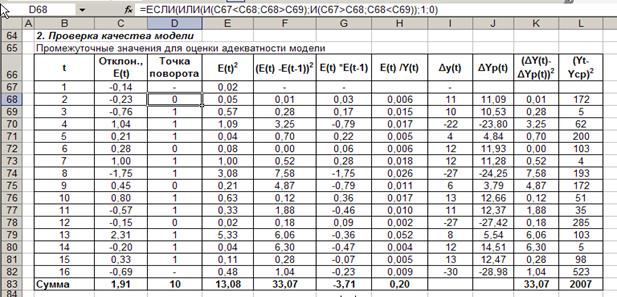
2) Проверка точности модели

,

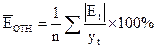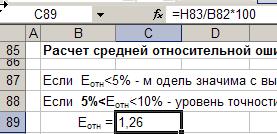
Е_отн<5% - модель значима с высокой степенью точности

3. Проверка адекватности модели

а) проверка случайности уровней:

Гипотеза подтверждается, если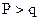, где 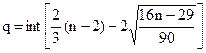. Функция int означает, что от полученного значения берется только целая часть. Тогда рассчитав, получим q= int (2/3*(16-2) -2*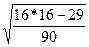) = 6.

Из таблицы Р = 10, т.е. можно заключить, что гипотеза выполнена.

б) проверка независимостей уровня ряда остатков (отсутствия автокорреляции)

- по критерию Дарбина - Уотсона: табличные значения d1 = 1,08, d2 = 1,36.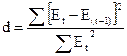  

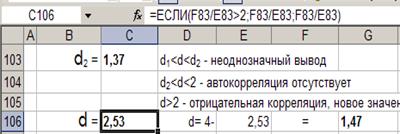
неоднозначный ответ

- по первому коэффициенту корреляции: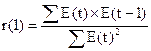

Критический уровень для N<15 (табличное значение) r_кр = 0,32,

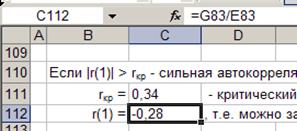
т.к. |r(1)| ≤ r_кр – сильная автокорреляция

в) Расчет нормальности распределения остаточной компоненты по RS-критерию с критическими уровнями 3 - 4,21

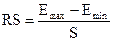, где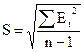

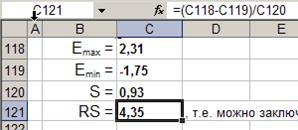
т.е. можно заключить, что распределение нормальное.

г) Значимость коэффициентов регрессии а_j оценим с помощью t-критерия Стьюдента: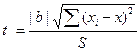

Табличное значение t для вероятности 95% и v1=n-k-1=14: tтабл=2,15

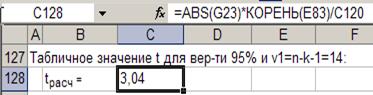
Т.к. t_расч>t_табл, то параметр b статистически значим

4. Построение точечного прогноза

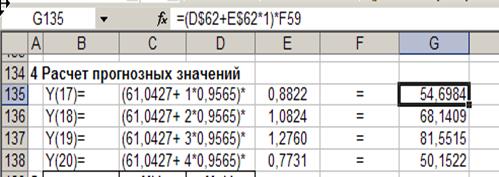
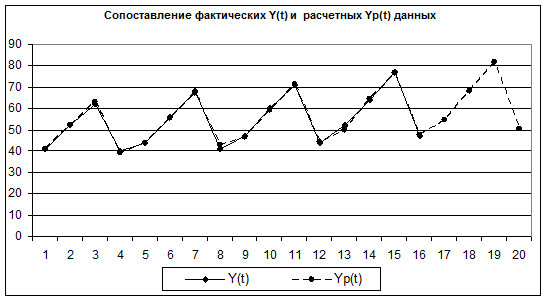
5.Отразим на графике расчетные, фактические и прогнозные данные.

Задание 2.

Даны цены (открытия, максимальная, минимальная и закрытия) за 10 дней. Интервал сглаживания принят равным пяти дням. Рассчитать:

- экспонциальную скользящую среднюю;

- момент;

- скорость изменения цен;

- индекс относительной силы;

- %R, %K, %D.

Расчеты проводить для всех дней, для которых эти расчеты можно выполнить на основании имеющихся данных.

Таблица № 2  -  Исходные данные.

Решение:

Введем исходные данные в ячейки В2:Е13.

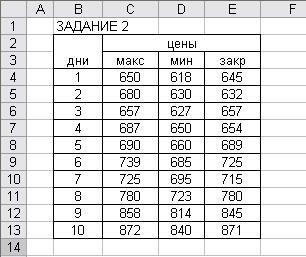
Расчет проведем в таблице.

Экспоненциальная скользящая средняя (ЕМА) определяется по формуле:

EMA_t = C_t*K + EMA_t-1*(1- K) ,

где  C_t - цена закрытия i-го дня ( i = (t –n +1),…,t);

n - интервал сглаживания (n = 5)

K = 2/(n+1) = 2/(5+1)= 0,33, запишем это значение в ячейку D$19.

ЕМА₅ = (С₁+С₂+С₃+С₄+С₅)/n, в ячейку С33 введем формулу: ==СУММ(B29:B33)/5.

ЕМА₆ =С₆*K+EMA₅*(1-K), в ячейку С34 введем формулу: =B34*D$19+C33*(1-D$19), аналогично заполним ячейки С35:С38  формулами. 

Момент (МОМ): МОМ_t = C_t - C_t-n

Положительное значение МОМ  свидетельствует о росте цен.

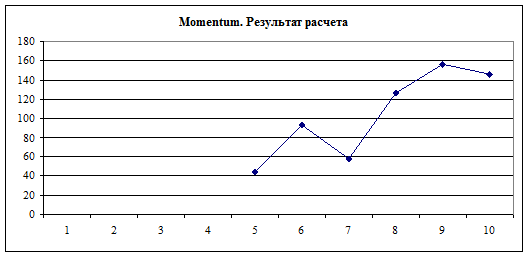
Движение графика вверх (7-9 день) в зону положительных значений является относительным сигналом к покупке, а движение графика вниз (9 - 10 день) в зону отрицательных значений является относительным сигналом к продаже.

Скорость изменения цен (ROC): ROC_t = C_t/C_t-n *100%

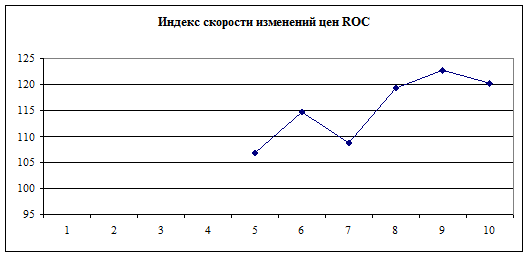
ROC является отражением скорости изменения цены , а также указывает направление этого изменения. В качестве нулевой линии используется уровень 100%. Нахождения индекса выше линии 100 и положительная динамика в 7-9 дни говорит о сигнале к покупке. На 7-8 день скорость изменения цен была максимальной.

Индекс относительной силы (RSI):

RSI = 100 - 100/(1+AU/AD),

где AU  - сумма приростов конечных цен за n дней;

AD - сумма убыли конечных цен за n дней.

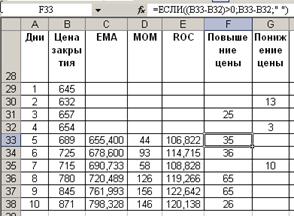
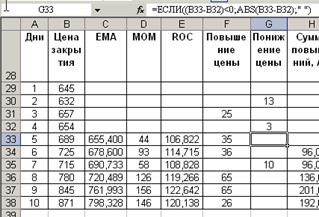
Рассчитаем сумму повышений:

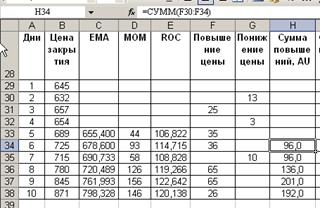
Рассчитаем сумма понижений:

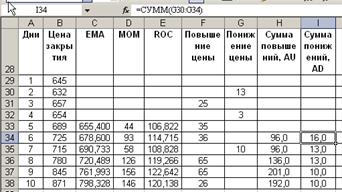
Индекс силы рассчитаем в ячейках J34:J38. В ячейку J34 введем формулу =100-100/(1+H34/I34), в остальных проделаем те же операции.

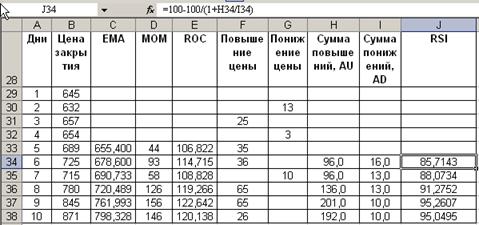
Зоны перепроданности располагаются обычно ниже 25-20, а перекупленности - выше 75-80. Сигналом служит разворот RSI в указанных зонах и выход из нее. Как видно из рисунка, индекс относительной силы вошел в зону, ограниченной линией 80%, на 6-10 день. Это значит, что цены поднялись слишком высоко, надо ждать их падения и подготовится к продаже. Сигналом к продаже послужит момент выхода графика из зоны перепроданности.

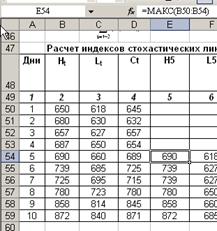
Стохастические линии

Смысл индексов %К и  %R состоит в том, что при росте цен цена закрытия бывает ближе к максимальной цена ,а при падении цен, наоборот, ближе к минимальной. Индексы %R и %К проверяют куда больше тяготеет цена закрытия.

Значение индекса текущего дня:

%К_t =100(C_t - L₅)/(H₅-L₅)

%R = (Ct-L5)/ (H5-L5)*100%

%

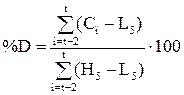L₅, H₅ - соответственно минимальная и максимальная цены за предшествующие 5 дней;

C_t – цена закрытия текущего дня.

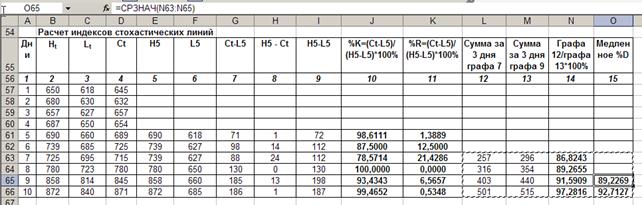
Критические значения %К практически во все дни анализа (зона перекупленности) свидетелствует о том, что можно ожидать скорого разворота тренда, т.е. падения цен. Как видно из графика и из таблицы  если цена закрытия ближе к максимальной цене, то наблюдается рост цен , в противном случае,падение.