Содержание
Введение. 3
1. Регрессионное моделирование и задача выбора
регрессионной модели. 4
2. Числовой пример сопоставления двух видов
регрессионных моделей. 7
Заключение. 16
Список литературы.. 17
Введение
Важнейшими задачами регрессионного анализа являются
выбор типа модели (формы связи), установление степени влияния независимых
переменных на зависимую и определение расчётных значений зависимой переменной
(функции регрессии).
Решение всех названных задач приводит к
необходимости комплексного использования этих методов.
Корреляционный и регрессионный анализ, исследование
связей в условиях массового наблюдения и действия случайных факторов
осуществляется, как правило, с помощью экономико-статистических моделей. В
широком смысле модель – это аналог, условный образ (изображение, описание,
схема, чертёж и т.п.) какого-либо объекта, процесса или события, приближенно
воссоздающий «оригинал». Модель представляет собой логическое или математическое
описание компонентов и функций, отображающих существенные свойства
моделируемого объекта или процесса, даёт возможность установить основные
закономерности изменения оригинала. В модели оперируют показателями,
исчисленными для качественно однородных массовых явлений (совокупностей).
Выражение и модели в виде функциональных уравнений используют для расчёта
средних значений моделируемого показателя по набору заданных величин и для
выявления степени влияния на него отдельных факторов.
1. Регрессионное
моделирование и задача выбора регрессионной модели
Важнейшим этапом построения регрессионной модели
(уравнения регрессии) является установление в анализе исходной информации
математической функции. Сложность заключается в том, что из множества функций
необходимо найти такую, которая лучше других выражает реально существующие
связи между анализируемыми признаками. Выбор типов функции может опираться на
теоретические знания об изучаемом явлении, опят предыдущих аналогичных
исследований, или осуществляться эмпирически – перебором и оценкой функций
разных типов и т.п.
При изучении связи экономических показателей
производства (деятельности) используют различного вида уравнения прямолинейной
и криволинейной связи. Наиболее распространенными и часто применяемыми моделями
регрессии являются линейная и степенная. Опишем их.
Внимание к линейным связям объясняется ограниченной
вариацией переменных и тем, что в большинстве случаев нелинейные формы связи
для выполнения расчётов преобразуют (путём логарифмирования или замены
переменных) в линейную форму. Уравнение однофакторной (парной) линейной
корреляционной связи имеет вид:
ŷ = a0 + a1x ,
где ŷ - теоретические значения результативного
признака, полученные по уравнению регрессии;
a0 , a1 - коэффициенты (параметры) уравнения
регрессии.
Поскольку a0 является средним значением у в точке
х=0, экономическая интерпретация часто затруднена или вообще невозможна.
Коэффициент парной линейной регрессии a1 имеет смысл
показателя силы связи между вариацией факторного признака х и вариацией
результативного признака у. Вышеприведенное уравнение показывает среднее
значение изменения результативного признака у при изменении факторного признака
х на одну единицу его измерения, то есть вариацию у, приходящуюся на единицу
вариации х. Знак a1 указывает направление этого изменения.
Параметры уравнения a0 , a1 находят методом
наименьших квадратов (метод решения систем уравнений, при котором в качестве
решения принимается точка минимума суммы квадратов отклонений), то есть в
основу этого метода положено требование минимальности сумм квадратов отклонений
эмпирических данных yi от выравненных ŷ :
S(yi – ŷ)2
= S(yi – a0 – a1xi)2 ® min
Для нахождения минимума данной функции приравняем к
нулю ее частные производные и получим систему двух линейных уравнений, которая
называется системой нормальных уравнений:
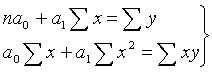
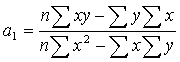
Решим эту систему в общем виде:
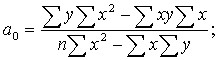
Или, что то же самое,
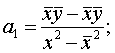
Параметры уравнения
парной линейной регрессии иногда удобно исчислять по следующим формулам, дающим
тот же результат:
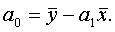
Уравнение степенной агрессии имеет вид:
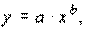
где a,
b – параметры, которые определяются по данным таблицы наблюдений.
Таблица
наблюдений составлена и имеет вид
|
x
|
x 1
|
x 2
|
...
|
x n
|
|
y
|
y 1
|
y 2
|
...
|
y n
|
Прологарифмируем
исходное уравнение и в результате получим
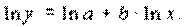
Обозначим
ln y через y' , ln a как a' , а
ln x как x' .
В результате
подстановки получим
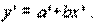
Данное уравнение есть не
что иное, как уравнение линейной регрессии, параметры которого мы умеем
находить.
Для этого
прологарифмируем исходные данные:
|
ln x
|
ln x 1
|
ln x 2
|
...
|
ln x n
|
|
ln y
|
ln y 1
|
ln y 2
|
...
|
ln y n
|
Далее необходимо
выполнить известные нам вычислительные процедуры по нахождению коэффициентов a
и b , используя прологарифмированные исходные данные. В результате
получим значения коэффициентов b и a' . Параметр a можно
найти по формуле
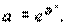
В этих же целях можно
воспользоваться функцией EXP в Excel.
2. Числовой пример сопоставления двух видов
регрессионных моделей
В этом разделе
контрольной работы приведем пример производственной ситуации, которая может
быть описана как с помощью линейной, так и с помощью степенной моделей
регрессии, а затем сравним эффективность (адекватность) этих моделей.
Вычисления проведем с помощью программы Excel, причем результаты вычислений
покажем как в режиме чисел, так и в режиме формул.
Исходные данные:
|
№
|
Удельный вес
рабочих со специальной подготовкой,
х
|
Удельный вес бракованной
продукции, %, y
|
|
1
|
15
|
18
|
|
2
|
25
|
12
|
|
3
|
35
|
10
|
|
4
|
45
|
8
|
|
5
|
55
|
6
|
|
6
|
65
|
5
|
|
7
|
70
|
4
|
|
8
|
80
|
3
|
|
9
|
90
|
2
|
|
10
|
95
|
1
|
В связи с необходимостью сравнения
двух моделей регрессии решим следующий круг задач:
1. Рассчитаем параметры уравнений
линейной, степенной парной регрессии. Поясним смысл коэффициентов.
2. Оценим тесноту связи с помощью
показателей корреляции и детерминации.
3. Оценим качество уравнений с
помощью средней ошибки аппроксимации.
4. Оценим с помощью F-критерия Фишера статистическую
надёжность результатов регрессионного моделирования, выберем лучшее уравнение
регрессии и дадим обоснование.
5. Применим выбранную модель для
прогнозе и сделаем вывод.
Решение:
Уравнение линейной
регрессии имеет вид:
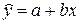, где 
, 
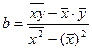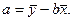
Для вычислений используем таблицу:
Режим числа:
|
|
x
|
y
|
x^2
|
x*y
|
y^2
|
|
1
|
15
|
18
|
225
|
270
|
324
|
|
2
|
25
|
12
|
625
|
300
|
144
|
|
3
|
35
|
10
|
1225
|
350
|
100
|
|
4
|
45
|
8
|
2025
|
360
|
64
|
|
5
|
55
|
6
|
3025
|
330
|
36
|
|
6
|
65
|
5
|
4225
|
325
|
25
|
|
7
|
70
|
4
|
4900
|
280
|
16
|
|
8
|
80
|
3
|
6400
|
240
|
9
|
|
9
|
90
|
2
|
8100
|
180
|
4
|
|
10
|
95
|
1
|
9025
|
95
|
1
|
|
итого
|
575
|
69
|
39775
|
2730
|
723
|
|
средние
|
57,5
|
6,9
|
3977,5
|
273
|
72,3
|
Режим формул:
|
x
|
y
|
x^2
|
x*y
|
y^2
|
|
1
|
15
|
18
|
=B2^2
|
=(B2*C2)
|
=C2^2
|
|
2
|
25
|
12
|
=B3^2
|
=(B3*C3)
|
=C3^2
|
|
3
|
35
|
10
|
=B4^2
|
=(B4*C4)
|
=C4^2
|
|
4
|
45
|
8
|
=B5^2
|
=(B5*C5)
|
=C5^2
|
|
5
|
55
|
6
|
=B6^2
|
=(B6*C6)
|
=C6^2
|
|
6
|
65
|
5
|
=B7^2
|
=(B7*C7)
|
=C7^2
|
|
7
|
70
|
4
|
=B8^2
|
=(B8*C8)
|
=C8^2
|
|
8
|
80
|
3
|
=B9^2
|
=(B9*C9)
|
=C9^2
|
|
9
|
90
|
2
|
=B10^2
|
=(B10*C10)
|
=C10^2
|
|
10
|
95
|
1
|
=B11^2
|
=(B11*C11)
|
=C11^2
|
|
итого
|
=СУММ(B2:B11)
|
=СУММ(C2:C11)
|
=СУММ(D2:D11)
|
=СУММ(E2:E11)
|
=СУММ(F2:F11)
|
|
средние
|
=B12/10
|
=C12/10
|
=D12/10
|
=E12/10
|
=F12/10
|
Получаем: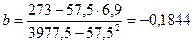 
, 
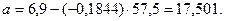
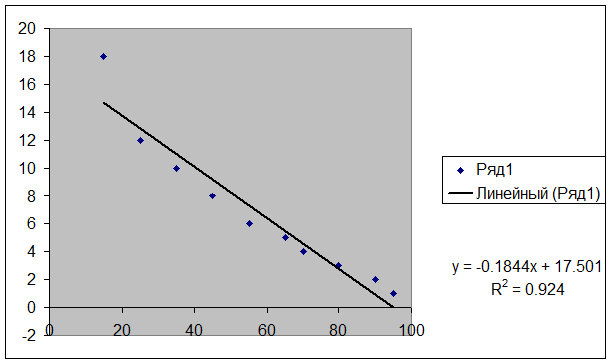
y = -0,1844x + 17,501 – уравнение
линейной регрессии.
Коэффициент –0,1844<0 показывает, что связь обратная.
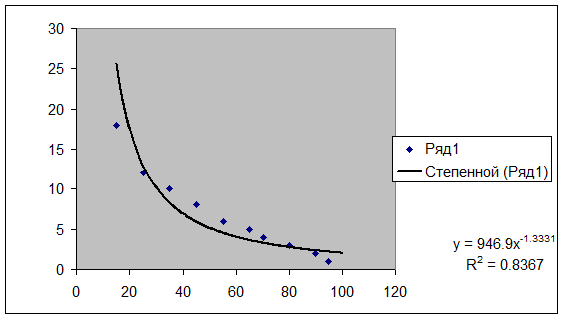
Уравнение степенной регрессии имеет вид:
,
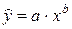Логарифмируя,
получаем уравнение линейной регрессии:
.
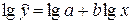Для вычислений используем таблицу:
Режим числа:
|
X=lgx
|
Y=lgy
|
X^2
|
X*Y
|
Y^2
|
|
1
|
1,176091
|
1,255273
|
1,383191
|
1,476315
|
1,575709
|
|
2
|
1,39794
|
1,079181
|
1,954236
|
1,508631
|
1,164632
|
|
3
|
1,544068
|
1
|
2,384146
|
1,544068
|
1
|
|
4
|
1,653213
|
0,90309
|
2,733112
|
1,493
|
0,815572
|
|
5
|
1,740363
|
0,778151
|
3,028862
|
1,354265
|
0,605519
|
|
6
|
1,812913
|
0,69897
|
3,286655
|
1,267172
|
0,488559
|
|
7
|
1,845098
|
0,60206
|
3,404387
|
1,11086
|
0,362476
|
|
8
|
1,90309
|
0,477121
|
3,621751
|
0,908005
|
0,227645
|
|
9
|
1,954243
|
0,30103
|
3,819064
|
0,588286
|
0,090619
|
|
10
|
1,977724
|
0
|
3,911391
|
0
|
0
|
|
итого
|
17,00474
|
7,094876
|
29,52679
|
11,2506
|
6,330731
|
|
средние
|
1,700474
|
0,709488
|
2,952679
|
1,12506
|
0,633073
|
Режим формул:
|
X=lgx
|
Y=lgy
|
X^2
|
X*Y
|
Y^2
|
|
1
|
=LOG10(B2)
|
=LOG10(C2)
|
=B17^2
|
=(B17*C17)
|
=C17^2
|
|
2
|
=LOG10(B3)
|
=LOG10(C3)
|
=B18^2
|
=(B18*C18)
|
=C18^2
|
|
3
|
=LOG10(B4)
|
=LOG10(C4)
|
=B19^2
|
=(B19*C19)
|
=C19^2
|
|
4
|
=LOG10(B5)
|
=LOG10(C5)
|
=B20^2
|
=(B20*C20)
|
=C20^2
|
|
5
|
=LOG10(B6)
|
=LOG10(C6)
|
=B21^2
|
=(B21*C21)
|
=C21^2
|
|
6
|
=LOG10(B7)
|
=LOG10(C7)
|
=B22^2
|
=(B22*C22)
|
=C22^2
|
|
7
|
=LOG10(B8)
|
=LOG10(C8)
|
=B23^2
|
=(B23*C23)
|
=C23^2
|
|
8
|
=LOG10(B9)
|
=LOG10(C9)
|
=B24^2
|
=(B24*C24)
|
=C24^2
|
|
9
|
=LOG10(B10)
|
=LOG10(C10)
|
=B25^2
|
=(B25*C25)
|
=C25^2
|
|
10
|
=LOG10(B11)
|
=LOG10(C11)
|
=B26^2
|
=(B26*C26)
|
=C26^2
|
|
итого
|
=СУММ(B17:B26)
|
=СУММ(C17:C26)
|
=СУММ(D17:D26)
|
=СУММ(E17:E26)
|
=СУММ(F17:F26)
|
|
средние
|
=B27/10
|
=C27/10
|
=D27/10
|
=E27/10
|
=F27/10
|
Получаем: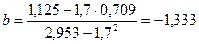 
,
, 
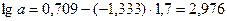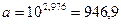
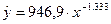– уравнение степенной регрессии.
1. Коэффициент корреляции: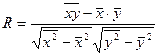 
.
Коэффициент детерминации: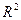 
.
Для линейной регрессии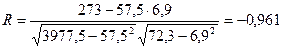 
.
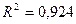Для степенной регрессии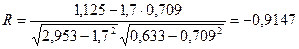 
.
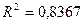Так как показатели корреляции и
детерминации близки к 1, то связь между x и y тесная.
2. Средняя ошибка аппроксимации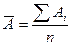 
, где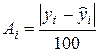 
Для расчетов
составляем таблицы:
Линейная регрессия
Режим числа:
|
x
|
y
|
yp
|
Ai
|
|
1
|
15
|
18
|
14,735
|
0,03265
|
|
2
|
25
|
12
|
12,891
|
0,00891
|
|
3
|
35
|
10
|
11,047
|
0,01047
|
|
4
|
45
|
8
|
9,203
|
0,01203
|
|
5
|
55
|
6
|
7,359
|
0,01359
|
|
6
|
65
|
5
|
5,515
|
0,00515
|
|
7
|
70
|
4
|
4,593
|
0,00593
|
|
8
|
80
|
3
|
2,749
|
0,00251
|
|
9
|
90
|
2
|
0,905
|
0,01095
|
|
10
|
95
|
1
|
-0,017
|
0,01017
|
|
итого
|
575
|
69
|
68,98
|
0,11236
|
|
средние
|
57,5
|
6,9
|
6,898
|
0,011236
|
Режим формул:
|
x
|
y
|
yp
|
Ai
|
|
1
|
15
|
18
|
=-0,1844*$B2+17,501
|
=ABS(C2-D2)/100
|
|
2
|
25
|
12
|
=-0,1844*$B3+17,501
|
=ABS(C3-D3)/100
|
|
3
|
35
|
10
|
=-0,1844*$B4+17,501
|
=ABS(C4-D4)/100
|
|
4
|
45
|
8
|
=-0,1844*$B5+17,501
|
=ABS(C5-D5)/100
|
|
5
|
55
|
6
|
=-0,1844*$B6+17,501
|
=ABS(C6-D6)/100
|
|
6
|
65
|
5
|
=-0,1844*$B7+17,501
|
=ABS(C7-D7)/100
|
|
7
|
70
|
4
|
=-0,1844*$B8+17,501
|
=ABS(C8-D8)/100
|
|
8
|
80
|
3
|
=-0,1844*$B9+17,501
|
=ABS(C9-D9)/100
|
|
9
|
90
|
2
|
=-0,1844*$B10+17,501
|
=ABS(C10-D10)/100
|
|
10
|
95
|
1
|
=-0,1844*$B11+17,501
|
=ABS(C11-D11)/100
|
|
итого
|
=СУММ(B2:B11)
|
=СУММ(C2:C11)
|
=СУММ(D2:D11)
|
=СУММ(E2:E11)
|
|
средние
|
=B12/10
|
=C12/10
|
=D12/10
|
=E12/10
|
Степенная регрессия
Режим числа:
|
x
|
y
|
yp
|
Ai
|
|
1
|
15
|
18
|
25,61279
|
0,076128
|
|
2
|
25
|
12
|
12,96314
|
0,009631
|
|
3
|
35
|
10
|
8,277649
|
0,017224
|
|
4
|
45
|
8
|
5,921156
|
0,020788
|
|
5
|
55
|
6
|
4,53134
|
0,014687
|
|
6
|
65
|
5
|
3,626681
|
0,013733
|
|
7
|
70
|
4
|
3,285519
|
0,007145
|
|
8
|
80
|
3
|
2,74976
|
0,002502
|
|
9
|
90
|
2
|
2,350192
|
0,003502
|
|
10
|
95
|
1
|
2,186758
|
0,011868
|
|
итого
|
575
|
69
|
71,50499
|
0,177208
|
|
средние
|
57,5
|
6,9
|
7,150499
|
0,017721
|
Режим формул:
|
|
x
|
y
|
yp
|
Ai
|
|
1
|
15
|
18
|
=946,9*B17^(-1,3331)
|
=ABS(C17-D17)/100
|
|
2
|
25
|
12
|
=946,9*B18^(-1,3331)
|
=ABS(C18-D18)/100
|
|
3
|
35
|
10
|
=946,9*B19^(-1,3331)
|
=ABS(C19-D19)/100
|
|
4
|
45
|
8
|
=946,9*B20^(-1,3331)
|
=ABS(C20-D20)/100
|
|
5
|
55
|
6
|
=946,9*B21^(-1,3331)
|
=ABS(C21-D21)/100
|
|
6
|
65
|
5
|
=946,9*B22^(-1,3331)
|
=ABS(C22-D22)/100
|
|
7
|
70
|
4
|
=946,9*B23^(-1,3331)
|
=ABS(C23-D23)/100
|
|
8
|
80
|
3
|
=946,9*B24^(-1,3331)
|
=ABS(C24-D24)/100
|
|
9
|
90
|
2
|
=946,9*B25^(-1,3331)
|
=ABS(C25-D25)/100
|
|
10
|
95
|
1
|
=946,9*B26^(-1,3331)
|
=ABS(C26-D26)/100
|
|
итого
|
=СУММ(B17:B26)
|
=СУММ(C17:C26)
|
=СУММ(D17:D26)
|
=СУММ(E17:E26)
|
|
средние
|
=B27/10
|
=C27/10
|
=D27/10
|
=E27/10
|
Средняя ошибка аппроксимации:
Для линейной регрессии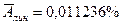 
.
Для степенной
регрессии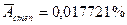 
.
Так как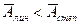 
, то более точным является уравнение линейной регрессии.
3.
Находим
значение F по формуле: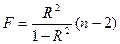 
Для линейной
регрессии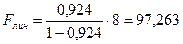 
.
Для степенной
регрессии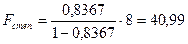 
.
По таблице для уровня
значимости 1% находим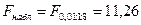 
.
Так как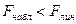 
и 
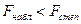, то оба уравнения
регрессии значимы при 1%-м уровне значимости.
Лучшим является уравнение
линейной регрессии, т.к.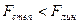 
.
4.
Прогнозное
значение удельного веса бракованной продукции найдем для x=10.
По уравнению линейной
регрессии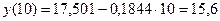 
.
По уравнению степенной
регрессии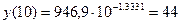 
.
Так как лучшим является
уравнение линейной регрессии, то более точным является прогноз: если удельный
вес рабочих со специальной подготовкой
Снизится до 10%, то
удельный вес бракованной продукции составит 15,6%.
5.
Вывод:
y = -0,1844x + 17,501 –
уравнение линейной регрессии
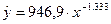– уравнение степенной регрессии.
Используя
результаты исследования уравнений с помощью показателей корреляции и
детерминации, средней ошибки аппроксимации, с помощью F-критерия Фишера заключаем,
что лучшим является уравнение линейной регрессии.
Заключение
Итак, в настоящей контрольной работе задача выбора
регрессионной модели проиллюстрирована на примере сравнения линейной и
степенной моделей однофакторной регрессии.
Помимо рассмотренных в контрольной работе, по
количеству включаемых факторов модели могут быть однофакторными и многофакторными
(два и более факторов).
В зависимости от познавательной цели статистические
модели подразделяются на структурные, динамические и модели связи.
Двухмерная линейная модель корреляционного и
регрессионного анализа (однофакторный линейный корреляционный и регрессионный
анализ). Наиболее разработанной в теории статистики является методология так
называемой парной корреляции, рассматривающая влияние вариации факторного
анализа х на результативный признак у и представляющая собой однофакторный
корреляционный и регрессионный анализ. Овладение теорией и практикой построения
и анализа двухмерной модели корреляционного и регрессионного анализа
представляет собой исходную основу для изучения многофакторных стохастических
связей.
Перечисленные виды регрессионных моделей сложны и
трудоемки для использования, однако, могут давать хорошие результаты при
математическом моделировании и прогнозировании математических явлений.
Список литературы
1
Артемьева
Е.Ю. Сборник задач по теории
вероятностей и математической статистике. – М.:
МГУ, 1969.
2
Гмурман
В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2004.
3
Гмурман
В.Е. Руководство к решению задач по теории вероятностей и математической статистике. –
М.: Высшая школа, 2001.
4
Лупандин
В.И. Математические методы в экономике. – М.: Финансы и статистика, 2003.
5
Суходольский
Г.В. Основы математической статистики
для экономистов. – М.: МГУ, 2003.