Фридман
М.Н.
Лекция
на тему:
ПРОВЕРКА
СТАТИСТИЧЕСКИХ ГИПОТЕЗ.
1. Принцип практической
уверенности.
Основой применения на практике большинства выводов и рекомендаций, полученных с помощью
математической статистики, лежит так
называемый принцип практической уверенности.
Суть его заключается в том, что при
однократном опыте редкое событие почти
наверняка не произойдет, и можно на практике действовать так, как будто
оно вообще невозможно.
Более строго мы можем сформулировать принцип
практической уверенности следующим образом:
Если вероятность 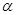 события А в данном испытании
очень мала, то при однократном выполнении испытания можно считать, что событие А
практически невозможно. Тогда противоположное событие
события А в данном испытании
очень мала, то при однократном выполнении испытания можно считать, что событие А
практически невозможно. Тогда противоположное событие 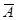 практически
достоверно, т.е обязательно произойдет.
практически
достоверно, т.е обязательно произойдет.
Вероятность 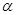 , которой решено пренебрегать, называется уровнем
значимости и устанавливается в
каждом отдельном случае с учетом важности последствий, вытекающих из
наступления события А.
, которой решено пренебрегать, называется уровнем
значимости и устанавливается в
каждом отдельном случае с учетом важности последствий, вытекающих из
наступления события А.
Так, например, если событие А заключается в том, что самолет не выпустит
шасси при посадке, то вряд ли мы полетим на таком самолете, зная, что это может
произойти в 5% случаев, те если 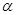 =0.05.
=0.05.
Однако для большинства экономических
задач уровень значимости 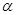 =0.05 является приемлемым.
=0.05 является приемлемым.
Обратим внимание, что в принципе
практической уверенности важно условие однократности опыта, т.к. при многократном
повторении опыта (n
раз) вероятность появления события А
хотя бы один раз (m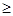 1) увеличивается в
n раз: Р( m
1) увеличивается в
n раз: Р( m 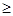 1)=1- (1-
1)=1- (1-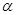 )n
)n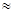 n
n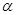 .
.
2.Статистическая
гипотеза и схема ее проверки.
Одним из важнейших практических применений математической
статистики является обоснование выбора
того или иного параметра или способа поведения, например, выбор
технологического процесса или способа инвестиций, эффективности управления или
значимости математической модели.
Как
правило, нас интересует некоторый признак X в генеральной совокупности, чей закон
распределения и (или) его параметры неизвестны.
Любое предположение о виде или параметрах неизвестного закона
распределения называется статистической
гипотезой.
Статистическая гипотеза бывает простой
или сложной.
Простая
гипотеза, в отличие от сложной, полностью определяет закон распределения
случайной величины. Например, гипотеза
«случайная величина распределена
по закону Пуассона с математическим ожиданием 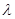 =2» является простой, а гипотеза «закон распределения не
является биномиальным» -сложной.
=2» является простой, а гипотеза «закон распределения не
является биномиальным» -сложной.
Выдвинутая гипотеза обычно обозначается 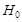 (нулевая гипотеза).
(нулевая гипотеза).
Утверждение,
которое является логическим отрицанием гипотезы 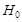 , называется
альтернативной , или конкурирующей.
, называется
альтернативной , или конкурирующей.
Как статистически проверить правильность выдвинутой гипотезы,
т.е. как разумно сделать вывод - отвергнуть ее или нет?
Для этого осуществляется случайная выборка и
используется некоторая случайная величина 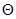 , закон распределения которой известен. Она, как правило,
характеризует степень расхождения фактически наблюдаемыми и предполагаемыми
характеристиками в соответствии с предполагаемой гипотезой.
, закон распределения которой известен. Она, как правило,
характеризует степень расхождения фактически наблюдаемыми и предполагаемыми
характеристиками в соответствии с предполагаемой гипотезой.
Значение этой случайной величины, 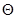
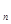 , полученное в результате выборки, сравнивается с так
называемым критическим значением
, полученное в результате выборки, сравнивается с так
называемым критическим значением 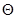
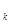 , которое установлено из условия: если гипотеза
, которое установлено из условия: если гипотеза 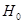 верна, то
вероятность Р (
верна, то
вероятность Р (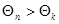 )=
)=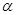 мала.
мала.
Поэтому в соответствии с принципом практической
уверенности это событие можно считать
практически невозможным.
Таким образом, если это событие (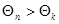 ) все же произошло в
данном конкретном опыте, то гипотеза
) все же произошло в
данном конкретном опыте, то гипотеза 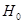 отвергается. Появление противоположного события(
отвергается. Появление противоположного события(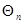
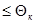 ) считается совместимым с гипотезой
) считается совместимым с гипотезой 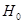 , она не отвергается.
, она не отвергается.
Правило, по которому гипотеза 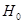 отвергается или нет, называется статистическим критерием (
тестом). Статистические критерии, служащие для проверки гипотез о законе
распределения, называемого критериями согласия.
отвергается или нет, называется статистическим критерием (
тестом). Статистические критерии, служащие для проверки гипотез о законе
распределения, называемого критериями согласия.
С каждым критерием связана случайная
величина 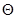 , называемая статистикой данного критерия. Эта
случайная величина имеет известный закон распределения, и она, как уже было
сказано, отражает расхождение выборочных результатов от тех, которые
соответствуют гипотезе
, называемая статистикой данного критерия. Эта
случайная величина имеет известный закон распределения, и она, как уже было
сказано, отражает расхождение выборочных результатов от тех, которые
соответствуют гипотезе 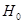 .
.
Поэтому множество всех значений
статистики критерия разбивается на две области: критическую (область отклонения
гипотезы ) W и область допустимых значений ( область
принятия гипотезы) 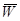 .
.
Если фактически наблюдаемое значение
статистики критерия попадает в критическую область W, то гипотезу 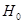 отвергают.
отвергают.
При этом
возможны следующие варианты:
Табл.1
|
Гипотеза Н
|
Принимается
|
Отвергается
|
|
Верна
|
Правильно
|
Ошибка
1 рода
|
|
Неверна
|
Ошибка
2 рода
|
Правильно
|
Вероятность 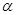 допустить ошибку
первого рода, те отвергнуть гипотезу
допустить ошибку
первого рода, те отвергнуть гипотезу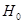 , когда она верна, называется уровнем
значимости, или размером критерия.
, когда она верна, называется уровнем
значимости, или размером критерия.
Вероятность допустить ошибку 2
рода, те принять неверную гипотезу 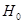 , обозначают
, обозначают 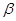 .
.
Вероятность (1-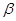 ) не допустить ошибку 2-го рода, т.е. отвергнуть гипотезу
) не допустить ошибку 2-го рода, т.е. отвергнуть гипотезу 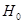 , когда она неверна, называется мощностью критерия.
, когда она неверна, называется мощностью критерия.
Вероятности ошибок 1 и 2 рода однозначно
определяются выбором критической
области. Конечно, желательно сделать эти ошибки как можно меньше, но, к
сожалению, при фиксированном объеме выборки
уменьшение одной из них ведет к увеличению другой.
Поэтому при выборе критической области
руководствуются принципом: при заданном уровне значимости 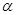 мощность критерия 1-
мощность критерия 1-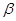 должна быть
максимальной.
должна быть
максимальной.
В рамки нашего курса не входит
рассмотрение условий существования таких
критериев.
Далее мы рассмотрим конкретный пример
постановки и проверки гипотезы.
3. Построение
теоретического закона распределения по опытным данным.
Проверка гипотезы о нормальном законе распределения.
Критерий 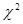 Пирсона.
Пирсона.
Одной из важнейших задач математической
статистики является установление закона распределения случайной величины Х,
характеризующей изучаемый признак, по
результатам случайной выборки.
Прежде всего выдвигается предположение о виде закона
распределения
(нормальный,
биномиальный или иной), исходя из теоретических предпосылок, предыдущих опытов и даже графического изображения
эмпирического распределения.
Вместо неизвестных параметров выбранного
закона распределения берут, как правило, их выборочные оценки, полученные по
выборке.
Между подобранным теоретическим и
эмпирическим законами распределения существуют расхождения. Возникает вопрос -
являются ли эти расхождения случайными, связанными с тем, что рассматривается
лишь выборка, а не вся генеральная совокупность, либо эти расхождения
существенны и связаны с неудачным выбором теоретического закона распределения.
Для ответа на этот вопрос служат критерии согласия .
Т.е. выдвигается гипотеза 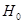 о том, что
исследуемая случайная величина Х подчиняется определенному закону
распределения. Для проверки этой гипотезы выбирается некоторый статистический
критерий, статистика которого U характеризует степень расхождения
теоретического и эмпирического распределения.
о том, что
исследуемая случайная величина Х подчиняется определенному закону
распределения. Для проверки этой гипотезы выбирается некоторый статистический
критерий, статистика которого U характеризует степень расхождения
теоретического и эмпирического распределения.
Закон распределения этой
статистики известен для достаточно большого
объема выборки n, и практически не зависит от закона
распределения Х.
Наиболее часто встречается задача
проверки гипотезы 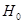 о нормальном
законе распределения случайной величины Х с параметрами - математическим ожиданием
о нормальном
законе распределения случайной величины Х с параметрами - математическим ожиданием 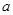 и дисперсией
и дисперсией 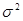 , которые
при достаточно большом объеме наблюдений заменяются их выборочными оценками - выборочной
средней и выборочной дисперсией :
, которые
при достаточно большом объеме наблюдений заменяются их выборочными оценками - выборочной
средней и выборочной дисперсией :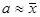 и
и 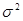
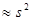 .
.
В качестве критерия согласия
используется 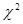 -критерий Пирсона, статистика которого U =
-критерий Пирсона, статистика которого U =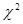 =
=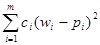 является суммой
квадратов отклонений частостей
является суммой
квадратов отклонений частостей ( статистических
вероятностей )
( статистических
вероятностей ) 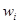 от гипотетических
вероятностей
от гипотетических
вероятностей 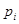 , рассчитанных в предположении о нормальном законе
распределения, взятых с некоторыми весами
, рассчитанных в предположении о нормальном законе
распределения, взятых с некоторыми весами 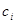 .
.
Можно
доказать, что если веса 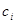 =
=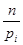 , то при достаточно большом n
статистика U=
, то при достаточно большом n
статистика U=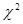 =
=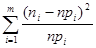 (1) имеет
(1) имеет 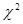 -распределение с r=m-r-1 степенями свободы, где m- число интервалов эмпирического вариационного ряда, r- число параметров теоретического
распределения, вычисленных по выборке; в
нашем случае r=2
(
-распределение с r=m-r-1 степенями свободы, где m- число интервалов эмпирического вариационного ряда, r- число параметров теоретического
распределения, вычисленных по выборке; в
нашем случае r=2
( 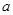 и
и 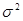 ).
).
Числа 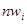 и
и 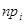 называются
соответственно эмпирическими и
теоретическими частотами.
называются
соответственно эмпирическими и
теоретическими частотами.
Эмпирические частости 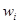 попадания случайной
величины в интервал
попадания случайной
величины в интервал
( 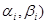 ) получаются в результате опытов, а соответствующие теоретические вероятности
) получаются в результате опытов, а соответствующие теоретические вероятности 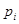 вычисляются в
предположении о нормальном законе распределения по формулам:
вычисляются в
предположении о нормальном законе распределения по формулам:
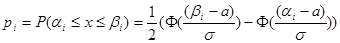
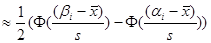 . (2)
. (2)
Схема применения критерия Пирсона для
проверки гипотезы о нормальном распределении такова:
- По формуле (1) вычисляется мера расхождения между
эмпирическими и теоретическими частотами- фактическое значение
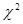 .
.
- Для установленного уровня
значимости
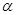 по таблице
по таблице 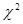 -распределения на стр.535 учебника находим критическое
значение
-распределения на стр.535 учебника находим критическое
значение 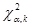 при числе
степеней свободы k.
при числе
степеней свободы k.
- Если фактически наблюдаемое
значение
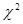 больше
критического
больше
критического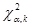 ,то гипотеза
,то гипотеза 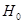 о нормальном законе с данными параметрами отвергается, в
противном случае она не противоречит опытным данным.
о нормальном законе с данными параметрами отвергается, в
противном случае она не противоречит опытным данным.
Пример 1.
С целью изучения времени бесперебойной
работы ткацких станков X
была произведена выборка объема n=100 станков из
10000. полученные данные приведены в таблице 2. По результатам выборки получены
следующие значения: среднее выборочное время бесперебойной работы станка 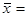 42 час, выборочная дисперсия
42 час, выборочная дисперсия 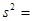 81, соответственно,
среднее квадратическое отклонение s=9 час.
81, соответственно,
среднее квадратическое отклонение s=9 час.
Проверить
гипотезу 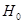 о нормальном распределении
случайной величины X с параметрами
о нормальном распределении
случайной величины X с параметрами 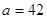 и
и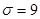 при уровне значимости
при уровне значимости 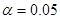 .
.
Табл.2
|
Время час.
|
Количество
станков 
|
|
20-30
|
10
|
|
30-40
|
30
|
|
40-50
|
40
|
|
50-60
|
20
|
|
Всего n=100
|
Решение.
Вычислим
теоретические частости (вероятности) по формуле 2.
Например,
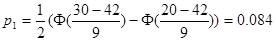
Аналогично
вычисляются и остальные вероятности.
Дополним
таблицу 2 следующим образом:
|
Время час.
|
Количество
станков 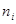
|
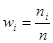
|
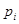
|
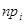
|
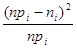
|
|
20-30
|
10
|
0.10
|
0.084
|
8.40
|
0.3
|
|
30-40
|
30
|
0.30
|
0.3212
|
32.12
|
0.13
|
|
40-50
|
40
|
0.40
|
0.4003
|
40.03
|
0
|
|
50-60
|
20
|
0.20
|
0.164
|
16.40
|
0.79
|
|
Всего n=100
|
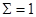
|
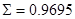
|
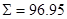
|
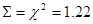
|
Таким
образом, фактическое значение 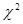 =1.22.
=1.22.
Находим по
таблице в учебнике на стр .535
критическое значение 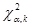 при
при 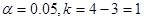 :
: 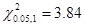 .
.
Так как ,
фактическое значение 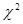
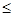
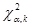 , то гипотеза
, то гипотеза 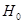 не отвергается!
не отвергается!
Для графического изображения
эмпирического и выравнивающего его теоретического нормального распределений можно
построить гистограмму и график плотности
нормального закона, однако необходимо использовать одинаковый масштаб по оси
ординат. Подробнее это изложено в
учебнике на
стр. 361.
Для
построения гистограммы можно по оси ординат откладывать частости 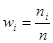 , а для выравнивающей кривой
по оси ординат значения плотности
( в масштабе) можно заменить вероятностями
, а для выравнивающей кривой
по оси ординат значения плотности
( в масштабе) можно заменить вероятностями 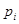 , причем соответствующие абсциссы совпадают с серединами
интервалов
, причем соответствующие абсциссы совпадают с серединами
интервалов 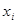 .
.
При
этом надо учесть, что максимум этой кривой будет в точке с абсциссой 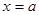 и ординатой
и ординатой 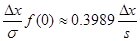 .
.
Для
примера 1 построим графики эмпирического и выравнивающего его
теоретического нормального распределений:
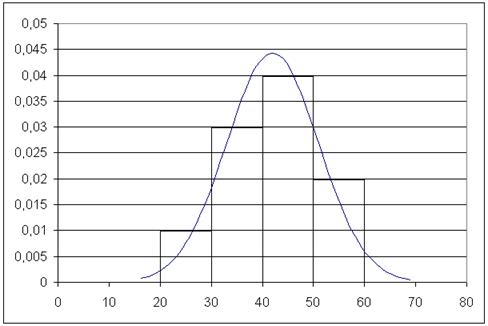
В данном случае максимум
выравнивающей кривой достигается в точке с координатами (42;0.44).