Задача 8.

Найти частное решение дифференциального уравнения , удовлетворяющего начальному условию у(0) = 0.

Решение.

Преобразуем уравнение: .

Данное дифференциальное уравнение - уравнение 1-го порядка, линейное относительно неизвестной функции у.

Применяя метод Бернулли для решения этого уравнения, сделаем  замену

у(х) = и(х) v(х),   где и{х) и v(х) - неизвестные функции, которые мы будем искать поочередно.

Согласно правилу дифференцирования произведения, имеем: у' = и'v +иv’.

Подставляя выражения для у и у' в исходное уравнение, получим: .

Отсюда           (*)

Выражение в скобках зависит только от v(х). Будем искать v(х), исходя из условия: .

Рассматривая это равенство как дифференциальное уравнение, найдём частное решение для у(х) методом разделения переменных:

.

Переходим к интегралу:

Подставим найденную функцию v{х) в уравнение (*):

Найдём теперь общее решение для неизвестной функции и(х):

Окончательно, имеем общее решение исходного дифференциального уравнения:

Теперь, используем данное начальное условие и найдём частное решение уравнения:

Отсюда .

Ответ: частное решение дифференциального уравнения имеет вид:

 

Задача 9.

Найти область сходимости степенного ряда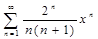    

Решение.

Общий вид степенного ряда . В нашем  случае

Известно, что область сходимости степенного ряда определяется величиной радиуса сходимости .

Сходимость ряда на границах необходимо исследовать дополнительно.

Найдем радиус сходимости ряда, используя формулу Даламбера: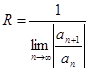

Имеем ;

 ;  .

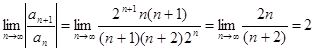Проверим сходимость ряда при  . Подставляя это значение в исходный ряд, получим числовой ряд  

Этот ряд сходится, так как сходится ряд  (по признаку сравнения).

Проверим сходимость ряда при . Подставляя это значение в исходный ряд, получим числовой ряд

Этот ряд сходится (по признаку Лейбница).

Итак, мы получили область сходимости исходного ряда:

Задача 10.2.

В каждой из двух урн содержится 8 черных и 2 белых шара. Из второй урны наудачу извлечен один шар и переложен в первую. Найти вероятность того, что шар, извлеченный из первой урны, окажется черным.

Решение.

Пусть событие А – «шар, извлеченный из первой урны, окажется черным».

Введем гипотезы:

 - «из второй урны в первую переложен белый шар»,

 - «из второй урны в первую переложен черный шар».

Для нахождения вероятности Р(А) применяем формулу полной вероятности

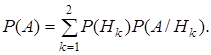
Так как во второй урне из 10 шаров 2 белых и 8 черных, то

  .

Если из второй урны в первую переложен белый шар, то в первой урне стало 11 шаров, из которых 8 черных. Получаем

Если из второй урны в первую переложен черный шар, то в первой урне стало 11 шаров, из которых 9 черных. Получаем

Подставляя в формулу полной вероятности найденные значения,  получаем:

.

 

Задача 12.2.

 Задан закон распределения дискретной случайной величины Х:

хi	8	12	18	24	30
pi	0,3	0,1	0,3	0,2	0,1

Требуется найти: а) математическое ожидание; б) дисперсию; в) среднее квадратическое отклонение дискретной случайной величины Х по заданному закону её распределения, заданному таблично (в первой строке таблицы указаны возможные значения, во второй строке — вероятности  возможных значений).

Решение.

Математическое ожидание:

=8*0,3+12*0,1+18*0,3+24*0,2+30*0,1=16,8.

Дисперсия:

=8²*0,3+12²*0,1+18²*0,3+24²*0,2+30²*0,1-16,8²=39,36

Среднее квадратическое отклонение:

 

Задача 13.2.

 В задаче заданы математическое ожидание а = 14  и среднее квадратическое отклонение s = 4 нормально распределённой случайной величины X. Требуется найти:

а) вероятность того, что Х примет значение, принадлежащее интервалу (10, 20);

 б) вероятность того, что абсолютная величина отклонения Х-а окажется меньше d = 4.

Решение.

а) Воспользуемся формулой:

По условию  следовательно,

Так как функция Лапласа нечетна, то .

Таким образом,  .

Вероятность того, что Х примет значение, принадлежащее интервалу (10, 20) равна 0,7745.

б) Воспользуемся формулой: .

Получаем: .

Вероятность того, что абсолютная величина отклонения Х-а окажется меньше d = 4 равна 0,6826.