Задание 1 (макс. 20 баллов)
Собрана статистика по курсу доллара в 76 обменных
пунктах в один момент времени. Результаты обработки приведены в таблице и на
диаграмме. Вы должны содержательно объяснить как можно большее число
показателей и элементов диаграммы.
Решение
Содержательное объяснение показателей таблицы:
|
Показатель
|
Значение
показателя
|
Содержательное объяснение показателя
|
|
Счет
|
76
|
Количество
элементов выборки (76 обменных пунктов).
|
|
Сумма
|
2280
|
Сумма
значений курса доллара во всех 76 обменных пунктах.
|
|
Минимум
|
28,72
|
Минимальное
значение курса доллара из выборки.
|
|
Максимум
|
30,47
|
Максимальное
значение курса доллара из выборки.
|
|
Интервал
|
1,75
|
Разность
между максимальным и минимальным значениями курса доллара из выборки.
|
|
Среднее
|
30
|
Среднее
арифметическое значений курса доллара во всех 76 обменных пунктах.
|
|
Медиана
|
30,01
|
Значение
курса доллара, делящее численность вариационного ряда по сумме накопленных частот на две равные
части.
|
|
Мода
|
29,91
|
Значение
курса доллара, имеющее наибольшую частоту.
|
|
Асимметричность
|
-1,1
|
Разность
между модой и медианой.
|
|
Дисперсия
выборки
|
0,08
|
Характеризует
разброс значений случайной величины относительно ее среднего значения.
|
Диаграмма частот показывает количество обменных
пунктов, имеющих определенное значение курса доллара:
-
в одном пункте
курс доллара равен 28,72;
-
в 7 пунктах курс
доллара равен 29,65;
-
в 13 пунктах
курс доллара равен 29,89;
-
в 17 пунктах
курс доллара равен 30;
-
в 13 пунктах
курс доллара равен 30,12;
-
в 9 пунктах курс
доллара равен 30,24;
-
в 8 пунктах курс
доллара равен 30,35;
-
в 7 пунктах курс
доллара равен 30,47;
-
в 1 пункте курс
доллара отличен от перечисленных.
На графике интегрального % показано количество
обменных пунктов (в %), имеющих курс доллара меньше значения по горизонтальной
оси. Например, 67% обменных пунктов
имеют курс доллара меньше 30,12.
Задание 2 (макс. 20 баллов)
В результате выборочного обследования зафиксировано
количество продаж одного товара разных фирм.
Требуется
с помощью критерия Пирсона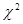 
проверить гипотезу о
том, что товары этих фирм продаются примерно одинаково, а отклонения -
случайны.
|
Фирма 1
Фирма 2
Фирма 3
Фирма 4
Фирма 5
|
180
250
203
196
206
|
Решение
Определим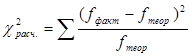 
.
Так как
проверяется гипотеза о том, что товары этих фирм продаются примерно одинаково,
а отклонения – случайны, то для нахождения теоретических значений
используем формулу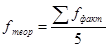 
.
Составляем расчетную таблицу.
|
|
|
|
|
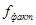
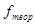
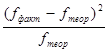
Фирма 1
Фирма 2
Фирма 3
Фирма 4
Фирма 5
|
180
250
203
196
206
|
207
207
207
207
207
|
3,522
8,932
0,077
0,585
0,005
|
|
Сумма
|
1035
|
|
13,121
|
С
помощью таблицы получаем: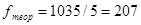 
,
, 
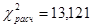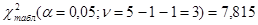
Так как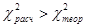 
, то нельзя считать, что товары фирм продаются примерно одинаково, а отклонения –
случайны.
Задание З (макс. 20 баллов)
В супермаркете проведено выборочное
маркетинговое обследование. Результаты приведены в таблице. Требуется с помощью
критерия Пирсона 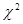проверить гипотезу о
том, что количество товаров в корзине не зависит от возраста покупателя.
|
Возраст
|
Количество товаров в
корзине
|
|
Корзина пуста
|
В корзине только
один товар
|
В корзине два и
более товара
|
|
Интервал -1. От 18.00, меньше 35.50
|
92
|
80
|
182
|
|
Интервал - 2. От 35.50, меньше 53.00
|
83
|
92
|
204
|
|
Интервал - 3 От 53.00, меньше 70.50
|
67
|
88
|
163
|
|
Интервал - 4 От 70.50, до 88.00
|
10
|
9
|
27
|
Решение
1. Проверяем услови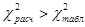е: 
, где
.
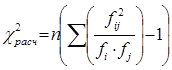Составляем вспомогательную таблицу.
|
|
|
|
|
|
|
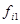
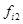
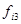
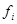
Интервал -1.
|
|
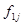
92
|
80
|
182
|
354
|
|
Интервал - 2.
|
|
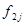
83
|
92
|
204
|
379
|
|
Интервал - 3
|
|
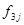
67
|
88
|
163
|
318
|
|
Интервал - 4
|
|
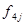
10
|
9
|
27
|
46
|
|
|
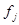
252
|
269
|
576
|
1097
|
Получаем:
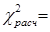1097*((0,0949+0,0672+0,1624+0,0721+0,0830+0,1906+0,0560+0,0905+
0,1451+0,0086+0,0065+0,0275)-1)=
1097*0,0046=5,052
.
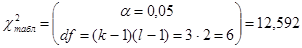Так как 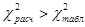, то количество товаров в корзине зависит от возраста покупателя.
Задание 4 (макс. 40 баллов)
Имеется статистика о количестве
зарегистрированных транспортных средств и аварийности на дорогах. Исследователь
провёл анализ этих данных. Результаты показаны на рисунке 1 и в таблицах 2-4.
Ваша задача описать в виде текста полученные
результаты. Вы должны содержательно объяснить как можно большее число
показателей и элементов диаграммы и сформулировать, выводы.
Решение
На рисунке 1 построена диаграмма рассеяния, т.е. для
каждого года изображена точка с координатами (х,у), где х - количество
зарегистрированных транспортных средств, у - количество аварий на дорогах. Для
исследования зависимости между количеством зарегистрированных транспортных
средств и количеством аварий на дорогах
к диаграмме рассеяния добавлена прямая линейного тренда, показано уравнение
тренда (у = 0,312х + 55,853) и коэффициент детерминации (R2 = 0,9362).
По уравнению линейного тренда можно сделать вывод о
прямой зависимости между количеством зарегистрированных транспортных средств и
количеством аварий на дорогах (т.к. b = 0,312 >0), т.е. при увеличении количества
зарегистрированных транспортных средств 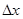на 
количество аварий на
дорогах увеличивается в среднем на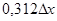 
.
Так как коэффициент детерминации R2 = 0,9362, то количество
аварий на дорогах на 93,62% зависит от количества зарегистрированных
транспортных средств. Связь между исследуемыми признаками тесная, т.к. R2 близок к 1.
В таблице 2 приведены результаты регрессионной
статистики.
Содержательное объяснение показателей таблицы:
|
Показатель
|
Значение
показателя
|
Содержательное объяснение показателя
|
Множественный
|
0,97
|
Коэффициент
корреляции. Так как R >0, то связь
между исследуемыми признаками прямая.
|
|
R-квадрат
|
0,94
|
Коэффициент
детерминации.
|
|
Нормированный
R-квадрат
|
0,93
|
Нормированный коэффициент
детерминации получается из коэффициента
детерминации поправкой на размер выборки.
|
|
Наблюдения
|
11
|
Количество элементов выборки (11 лет)
|
В таблице 3 приведены результаты дисперсионного
анализа. Общая дисперсия (разброс значений зависимой переменной у
относительно ее среднего значения) равна 17619,6. Большая часть дисперсии переменной у
(16495,4) объясняется
влиянием фактора х. Остаточная дисперсия равна 1124,1.
В таблице 4 приведены результаты исследования
коэффициентов регрессии. Определено, что для исследуемых признаков уравнение
регрессии у = bх + a имеет вид у
= 0,31х + 55,85. С вероятностью 0,95 значение коэффициента а уравнения
регрессии находится в интервале (23,07; 88,63), стандартная ошибка коэффициента
а равна 14,49. С
вероятностью 0,95 значение коэффициента b уравнения регрессии находится в интервале (0,25;
0,37), стандартная ошибка коэффициента b
равна 0,03.