Содержание




1. Детерминированные и вероятностные математические модели в экономике. Преимущества и недостатки. 3

2. Постановка задачи линейного программирования на примере задачи о пищевом рационе. Числовой пример. 5

3. Понятие эластичного спроса – математический и экономический смысл. Пример эластичного и неэластичного спроса. 10

Список литературы.. 17



1. Детерминированные и вероятностные математические модели в экономике. Преимущества и недостатки

 

Методы исследования экономических процессов базируются на использовании математических – детерминированных и вероятностных – моделей, представляющих изучаемый процесс, систему или вид деятельности. Такие модели дают количественную характеристику проблемы и служат основой для принятия управленческого решения при поисках оптимального варианта. Насколько обоснованы эти решения, являются ли  они лучшими из возможных, учтены ли и взвешены все факторы, определяющие оптимальное решение, каков критерий, позволяющий определить, что данное решение действительно наилучшее, - таков круг вопросов, имеющих большое значение для руководителей производства, и ответ на которые можно найти с помощью методов исследования операций.[1]

Одним из принципов формирования системы управления – метод кибернетических (математических) моделей. Математическое моделирование занимает промежуточное положение между экспериментом и теорией: нет необходимости строить реальную физическую модель системы, ее  заменит математическая модель. Особенность формирования системы управления заключается в вероятностном, статистическом подходе к процессам управления. В кибернетике принято, что любой процесс управления подвержен случайным, возмущающим воздействиям. Так, на производственный процесс оказывают влияния большое количество факторов, учесть которые детерминированным образом невозможно. Поэтому считается, что на производственный процесс воздействуют случайные сигналы. В силу этого планирование работы предприятия может быть только вероятностным.

По этим причинам часто, говоря о математическом моделировании экономических процессов, имеют в виду именно вероятностные модели.

Опишем каждый из типов математических моделей.

Детерминированные математические модели характеризуются тем, что описывают связь некоторых факторов с результативным показателем как функциональную зависимость, т. е. в детерминированных моделях результативный показатель модели представлен в виде произведения, частного, алгебраической суммы факторов, или в виде любой другой функции. Данный вид математических моделей наиболее распространен, поскольку, будучи достаточно простыми в применении (по сравнению вероятностными моделями), позволяет осознать логику действия основных факторов развития экономического процесса, количественно оценить их влияние, понять, какие факторы и в какой пропорции возможно и целесообразно изменить для повышения эффективности производства.

Вероятностные математические модели принципиально отличаются от детерминированных тем, что в вероятностным моделях взаимосвязь между факторами и результирующим признаком вероятностная (стохастическая): при  функциональной зависимости (детерминированные модели) одному и тому же состоянию факторов соответствует единственное состояние результирующего признака, тогда как в вероятностных моделях одному и тому же состоянию факторов соответствует целое множество состояний результирующего признака.[2]

Преимущество детерминированных моделей в простоте их применения. Основной недостаток – низкая адекватность реальной действительности, т.к., как было отмечено выше, большинство экономических процессов носит вероятностный характер.

Достоинством вероятностных моделей является то, что они, как правило, больше соответствуют реальной действительности (более адекватны), чем детерминированные. Однако, недостатком вероятностных моделей является сложность и трудоемкость их применения, так что во многих ситуациях достаточно бывает ограничится детерминированными моделями.


2. Постановка задачи линейного программирования на примере задачи о пищевом рационе. Числовой пример

Впервые постановка задачи линейного программирования в виде предложения по составлению оптимального плана перевозок; позволяющего минимизировать суммарной километраж, была дана в работе советского экономиста А. Н. Толстого в 1930 году.

Систематические исследования задач линейного программирования и разработка общих методов их решения получили дальнейшее развитие в работах российских математиков Л. В. Канторовича, В. С. Немчинова и других математиков и экономистов. Также методам  линейного программирования посвящено много работ зарубежных и прежде всего американских ученых.

Задача линейного программирования состоит в следующем: максимизировать (минимизировать) линейную функцию

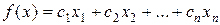, где 

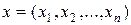
при ограничениях

                                                                (*)

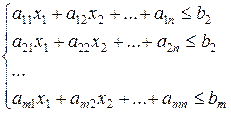причем все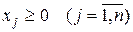

Замечание. Неравенства могут быть и противоположного смысла. Умножением соответствующих неравенств на (-1) можно всегда получить систему вида (*).

Если число переменных системы ограничений и целевой функции в математической модели задачи равно 2, то её можно решить графически.

Итак, надо максимизировать функцию 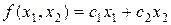 и удовлетворяющей системе ограничений.

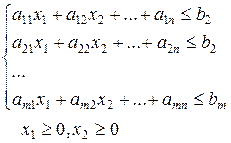
Обратимся к одному из неравенств системы ограничений.

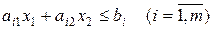
С геометрической точки зрения все точки, удовлетворяющие этому неравенству, должны либо лежать на прямой 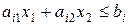, либо принадлежать одной из полуплоскостей, на которые разбивается плоскость этой прямой. Для того, чтобы выяснить это, надо проверить какая из  них содержит точку ().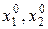

Замечание 2. Если 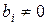, то проще взять точку (0;0).

Условия неотрицательности 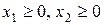  также определяют полуплоскости соответственно с граничными прямыми 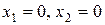. Будем считать, что система неравенств совместна, тогда полуплоскости, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты которых являются решением данной системы – это множество допустимых решений. Совокупность этих точек (решений) называется многоугольником решений. Он может быть точкой, лучом, многоугольником, неограниченной многоугольной областью. Таким образом, задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой целевая функция принимает максимальное (минимальное) значение. Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху (снизу). При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение. Для определения данной вершины построим прямую 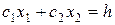 (где h – некоторая постоянная). Чаще всего берется прямая 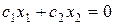. Остается выяснить направление движения данной прямой. Это направление определяется градиентом (антиградиентом) целевой функции

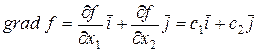
Вектор 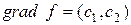 в каждой точке перпендикулярной прямой 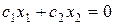, поэтому значение f будет возрастать при перемещении прямой в направлении градиента (убывать в направлении антиградиента). Для этого параллельно прямой  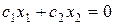проводим прямые, смещаясь в направлении градиента (антиградиента).

Эти построения будем продолжать до тех пор, пока прямая не пройдет через последнюю вершину многоугольника решений. Эта точка определяет оптимальное значение.

Итак, нахождение решения задачи линейного программирования геометрическим методом включает следующие этапы:

1.     Строят прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств.

2.     Находят полуплоскости, определяемые каждым из ограничений задачи.

3.     Находят многоугольник решений.

4.     Строят вектор .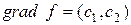

5.     Строят прямую .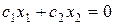

6.     Строят параллельные прямые 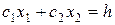 в направлении градиента или антиградиента, в результате чего находят точку, в которой функция принимает максимальное или минимальное значение, либо устанавливают неограниченность сверху (снизу) функции на допустимом множестве.

7.     Определяют координаты точки максимума (минимума) функции и вычисляют значение целевой функции в этой точке.

 

 

Задача о рациональном питании (задача о пищевом рационе).

ПОСТАНОВКА ЗАДАЧИ. Ферма производит откорм скота с коммерческой целью. Для простоты допустим, что имеется всего четыре вида продуктов: П1, П2, П3, П4; стоимость единицы каждого продукта равна соответственно С1, С2, С3, С4. Из этих продуктов требуется составить пищевой рацион, который должен содержать: белков – не менее bi единиц; углеводов – не менее b2 единиц; жиров – не менее b3 единиц. Для продуктов П1, П2, П3, П4 содержание белков, углеводов и жиров (в единицах на единицу продукта) известно и задано в таблице, где aij (i=1,2,3,4; j=1,2,3) – какие – то определённые числа; первый индекс указывает номер продукта, второй – номер элемента (белки, углеводы, жиры).

продукт

элементы

белки

углеводы

жиры

П1

П2

П3

П4

A11

A21

A31

A41

A12

A22

A32

A42

A13

A23

A33

A43

Требуется составить такой пищевой рацион (т.е. назначить количества продуктов П1, П2, П3, П4, входящих в него), чтобы условия по белкам, углеводам и жирам были выполнены и при этом стоимость рациона была минимальна.

МАТЕМАТИЧЕСКУЮ МОДЕЛЬ. Обозначим x1, x2, x3, x4 количества продуктов П1, П2, П3, П4, входящих в рацион. Показатель эффективности, который требуется минимизировать, - стоимость рациона (обозначим её L): она линейно зависит от элементов решения x1, x2, x3, x4.

Целевая функция: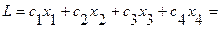

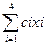
         Система ограничений:         

           a11x1+a21x2+a31x3+a41x4≥b1

         a12x1+a22x2+a32x3+a42x4≥b2               

         a13x1+a23x2+a32x3+a43x4≥b3

Эти линейные неравенства представляют собой ограничения, накладываемые на элементы решения x1, x2, x3, x4.

Таким образом, поставленная задача сводится к следующей: найти такие неотрицательные значения переменных x1, x2, x3, x4, чтобы они удовлетворяли ограничениям – неравенствам и одновременно обращали в минимум линейную функцию этих переменных:

                  


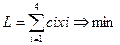
3. Понятие эластичного спроса – математический и экономический смысл. Пример эластичного и неэластичного спроса


Спрос изо­бра­жа­ет­ся в ви­де гра­фи­ка, по­ка­зы­ваю­ще­го ко­ли­че­ст­во про­дук­та, ко­то­рое по­тре­би­те­ли го­то­вы и в со­стоя­нии ку­пить по не­ко­то­рой це­не из воз­мож­ных в те­че­ние оп­ре­де­лен­но­го пе­рио­да вре­ме­ни цен. Спрос вы­ра­жа­ет ряд аль­тер­на­тив­ных воз­мож­но­стей, ко­то­рые мож­но пред­ста­вить в ви­де таб­ли­цы. Он по­ка­зы­ва­ет то ко­ли­че­ст­во про­дук­та, на ко­то­рое (при про­чих рав­ных ус­ло­ви­ях) бу­дет предъ­яв­лен спрос при раз­ных це­нах. Спрос по­ка­зы­ва­ет ко­ли­че­ст­во про­дук­та, ко­то­рое по­тре­би­те­ли бу­дут по­ку­пать по раз­ным воз­мож­ным це­нам, Це­на спро­са —  мак­си­маль­ная це­на, по ко­то­рой по­тре­би­тель го­тов ку­пить дан­ную про­дук­цию.

Одной из характеристик спроса является его эластичность. Раскроем это понятие.

Существует зависимость между изменением цены и тем количеством товара, на которое люди увеличивают или уменьшают свои покупки. Это понятие обозначается как ценовая эластичность спроса. Эластичность означает интенсивность реакции покупателей. Если небольшое изменение цены сильно изменяет объем покупок, то спрос эластичен. Если даже большое изменение цены лишь ненамного изменяет объем покупок, то говорят, что спрос неэластичен.

Пример: цена масла увеличилась на 10%, что привело к сокращению количеству продаваемого масла на 5%. Эластичность спроса в этом случае равняется 5 %  /  10 % = 0,5.

Обозначим за Р – цену товара, за Q – объем продаж, и на графиках изобразим кривые спроса в случае различной его эластичности:

1.            Неэластичный спрос имеет место, когда приобретаемое количество товара увеличивается меньше, чем на 1% на каждый процент снижения цены этого товара (слабая реакция) (рис. 1). Математический смысл неэластичного спроса заключается в том, что зависимость между спросом и предложением выражается медленно убывающей функцией.


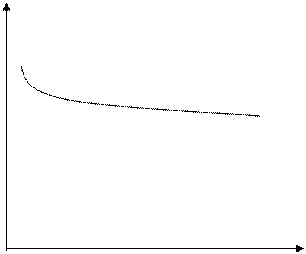                     Р               

                                                                                                           




                                                                                                  






                                                                                                   Q


 

Рис. 1. Неэластичный спрос



2.            Эластичный спрос имеет место, когда спрос возрастает больше, чем на 1 % на каждый 1% снижения цены (сильная реакция) (рис. 2). Математический смысл неэластичного спроса заключается в том, что зависимость между спросом и предложением выражается быстро убывающей функцией.


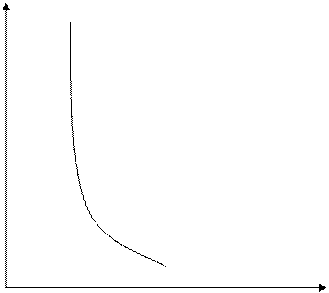                     Р





                                                                                                    




                                                                                                    





                                                                                                     Q   

Рис. 2. Эластичный спрос


3.            Единичная эластичность имеет место, когда покупаемое количество вырастает на 1 % при снижении цены на 1 % (рис. 3). Математический смысл неэластичного спроса заключается в том, что зависимость между спросом и предложением выражается линейной функцией.

Р

             







                                                                                                      







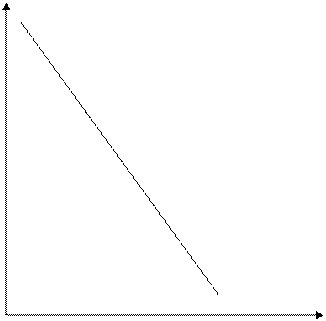
                                                                                                       Q

 

Рис. 3. Единичная эластичность спроса


Помимо перечисленных видов эластичности также выделяют совершенно (абсолютно) эластичный и совершенно (абсолютно) неэластичный спрос.

Если изменение цены не приводит ни к какому изменению количества спрашиваемой продукции, то такой спрос является совершенно неэластичным. С математической точки зрения эта ситуация описывается вырожденной функцией вида Q = Q0,  где Q0 – некоторое фиксированное значение спроса.

 




 

Рис. 4. Совершенно неэластичный спрос


Если самое малое снижение цены побуждает покупателей увеличивать покупки от нуля до предела своих возможностей, то такой спрос является совершенно эластичным. С математической точки зрения эта ситуация описывается вырожденной функцией вида P = P0,  где P0 – некоторое фиксированное значение цены.

 

 

 

 

 

 

Рис. 5. Совершенно эластичный спрос

Когда говорят об эластичности спроса, имеют в виду его эластичность по цене (ценовую эластичность).

Факторы ценовой эластичности спроса

- Заменяемость. Чем больше хороших заменителей данного продукта  предлагается потребителю, тем эластичнее бывает спрос на него. Эластичность спроса на продукт зависит от того,  насколько узко определены границы этого продукта.

- Удельный вес в доходе потребителя. Чем больше места занимает товар в бюджете потребителя, при прочих равных условиях, тем  выше эластичность спроса  на него.

- Предметы роскоши и предметы необходимости. Спрос на предметы необходимости обычно является неэластичным, спрос на предметы роскоши обычно эластичен.

- Фактор времени. Спрос на продукт более эластичен, чем длиннее время для принятия решений. Это зависит от привычек потребителя, долговечности продукта.[3]

Спрос на товар зависит не только от цены на этот же самый товар. Он зависит и от цен на другие товары. Данная зависимость характеризуется перекрестной эластичностью спроса по цене.[4]

Например, рост цены на бензин должен снижать спрос на автомобили. Повышение цены на хозяйственное мыло увеличивает спрос на стиральный порошок. Таким образом, перекрестная эластичность бывает и отрицательной, и положительной.

Эластичность спроса является чрезвычайно важным показателем для продавцов, которые хотят выявить последствия влияния изменения цен на полученную ими выручку. Когда эластичность спроса на какой-либо товар выше 1, то небольшое снижение цены увеличивает стоимость продаж и совокупную выручку. Наоборот, повышение цены имеет смысл при неэластичном спросе (эластичность спроса меньше 1). В этом случае возрастает стоимость продаж. При эластичном спросе (эластичность выше 1) нет смысла повышать цену, так как снизится объем продаж[5].

Теперь обратимся к эластичности спроса по доходам.

Рост дохода увеличивает возможность совершения покупок. Спрос на большинство товаров с увеличением дохода возрастает. Эластичность спроса на товары первой необходимости весьма мала (меньше 1), а на предметы роскоши – велика (больше 1). Кроме того, существуют товары, которые при достаточно высоком уровне доходов вытесняются лучшими товарами заменителями, спрос на них падает (товары низкого качества).

Таким образом, эластичность по доходу для некоторых товаров отрицательная[6].

Представляют интерес исследования А. Маршаллом проблем спроса на отдельные товары, точнее - разработанная им концепция эластичности спроса.

Лидер кембриджской школы поставил спрос на определённый товар в зависимость от трех главных факторов - предельной полезности, рыночной цены и денежного дохода, используемого на потребление, причём особое место отводилось первому из них.

Поскольку предельная полезность равна той максимальной цене, которую покупатель еще согласен уплатить за данный товар, она становится верхнем пределом колебания рыночной цены. Максимальная цена, утверждал А. Маршалл, является автономной, независимой от рынка ценой спроса и определяется только потребностью в товаре и его запасом. Если теперь взглянуть на рыночный процесс глазами покупателя (потребителя), то окажется, что именно от сюда, с точки цены спроса, рыночная цена, ведомая спросом и предложением, начинает свой долгий путь в сторону рыночного равновесия.

Пример эластичности спроса: предположим, что величины предельной полезности и дохода постоянны. Допустим, так же, что рыночная цена какого-то товара увеличилась (уменьшилась) на 1%, а спрос на него, испытывающий влияние этой цены, сократился (возрос) более чем на 1%. Тогда, по А. Маршаллу, движение спроса было эластичным по цене. Соответственно, спрос считался неэластичным, когда он менялся менее чем на 1% при однопроцентных колебаниях рыночной цены.

Концепция эластичности спроса имеет явные недостатки - выдвижение на первый план предельной полезности и её трактовка в духе австрийской школы, игнорирование социальной структуры общества, влияющей на распределение национального дохода, а стало быть, на покупательную способность групп населения. В то же время в целом ее можно считать научным достижением кембриджской школы.

Идеи А. Маршалла открыли дорогу обширному потоку прикладных исследований товарных рынков, практическое значение которых не вызывает сомнений.[7]


Список литературы


1.                 Гончаров В.В.  Важнейшие понятия и концепции в современном управлении. – М.: МНИИПУ, 2002. – 341 с.

2.                 История экономических учений / Под ред. Н.А. Хохлова. – СПб: Питер, 2002. – 324 с.

3.                 Нуриев, Н. Розанова. Поведение потребителя в рыночной экономике. Вопросы экономики № 1, 2003 год. – с. 4-9.

4.                 Казаков А.П., Минаев Н.В. Экономика. Курс лекций. Упражнения. Тесты и тренинги. – М.: Изд-во ЦИПКК АП, 1999. – 359 с.

5.                 Макроэкономика. Учебное пособие./ Под ред. А.М. Бункина. – М.: Инфра-М, 1995. – 337 с..

6.                 Социально-экономическая статистика / Под ред. Г.Л.Громыко. – М.: Изд-во МГУ, 1999. - 350 с.

7.                 Ховард К., Эриашвили Н.Д., Никитин А.М. Экономическая теория.  –М, 2000. – 564 с.

8.                 Чесноков С.В. Детерминационный анализ социально-экономических  данных. – М.: Наука. 1982. - 259 с.

9.                 Толстова Ю.Н. Логика математического анализа экономических процессов. –  М.: Наука, 2001. - 160 с.


[1] Чесноков С.В. Детерминационный анализ социально-экономических  данных. – М.: Наука. 1982. – с. 45.

[2] Толстова Ю.Н. Логика математического анализа экономических процессов. –  М.: Наука, 2001. – с. 32-33.

[3] Нуриев, Н. Розанова. Поведение потребителя в рыночной экономике. Вопросы экономики № 1, 2003 год. С. 4-9.

[4] Казаков А.П., Минаев Н.В. Экономика. Курс лекций. Упражнения. Тесты и тренинги. М.: Изд-во ЦИПКК АП, 1999. С. 21-22.

[5] Макроэкономика. Учебное пособие./ Под ред. А.М. Бункина. М., 1995. С. 72.

[6] Ховард К., Эриашвили Н.Д., Никитин А.М. Экономическая теория.  М, 2000. С.117.


[7] История экономических учений / Под ред. Н.А. Хохлова. СПб: Питер, 2002. С. 143.