Федеральное Агентство по Образованию
Государственное Образовательное Учреждение Высшего
Профессионального Образования
Всероссийский Заочный Финансово-Экономический Институт
Кафедра Статистики
КОНТРОЛЬНАЯ РАБОТА
ПО ДИСЦИПЛИНЕ
«СТАТИСТИКА»
Вариант №8
Исполнитель:
Специальность: Финансы и кредит,
2ВО, 3 курс
№ зачётной книжки:
Преподаватель:
Новороссийск
2007
Оглавление
Вариант 8. 3
ЗАДАНИЕ 1. 4
ЗАДАНИЕ 2. 8
ЗАДАНИЕ 3. 14
ЗАДАНИЕ 4. 15
Список используемой литературы: 16
Вариант 8
Имеются следующие выборочные данные о
деятельности российских коммерческих банков с ценными бумагами (выборка 2%-ная
механическая), млн. руб.:
Таблица 1
|
№ банка
п/п
|
Объём
вложений в ценные бумаги
|
Прибыль
|
|
1
|
2
|
3
|
|
1
|
1550
|
110
|
|
2
|
1910
|
174
|
|
3
|
1980
|
164
|
|
4
|
1450
|
159
|
|
5
|
1620
|
140
|
|
6
|
1750
|
156
|
|
7
|
1900
|
176
|
|
8
|
1640
|
169
|
|
9
|
1200
|
125
|
|
10
|
500
|
100
|
|
11
|
1100
|
137
|
|
12
|
2480
|
196
|
|
13
|
2610
|
227
|
|
14
|
1700
|
170
|
|
15
|
1050
|
139
|
|
16
|
700
|
132
|
|
17
|
1800
|
172
|
|
18
|
1940
|
175
|
|
19
|
2380
|
208
|
|
20
|
1860
|
168
|
|
21
|
2200
|
180
|
|
22
|
2490
|
200
|
|
23
|
1720
|
118
|
|
24
|
2900
|
217
|
|
25
|
1690
|
179
|
|
26
|
3300
|
270
|
|
27
|
2300
|
166
|
|
28
|
1580
|
141
|
|
29
|
3500
|
210
|
|
30
|
2800
|
222
|
ЗАДАНИЕ 1
По исходным данным:
1.
Постройте статистический ряд распределения предприятий по признаку – объём
вложений в ценные бумаги, образовав шесть групп с равными интервалами.
2. Постойте графики полученного ряда
распределения. Графически определите значения моды и медианы.
3. Рассчитайте характеристики
интервального ряда распределения: среднюю арифметическую, среднее
квадратическое отклонение, коэффициент вариации, моду и медиану.
4. Вычислите среднюю арифметическую по
исходным данным, сравните ее с аналогичным показателем, рассчитанным в п. 3 для
интервального ряда распределения. Объясните причину их расхождения.
Сделайте выводы по результатам выполнения
задания.
Решение:
1. Сначала определяем длину
интервала или шаг интервала по формуле:
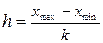 ,
,
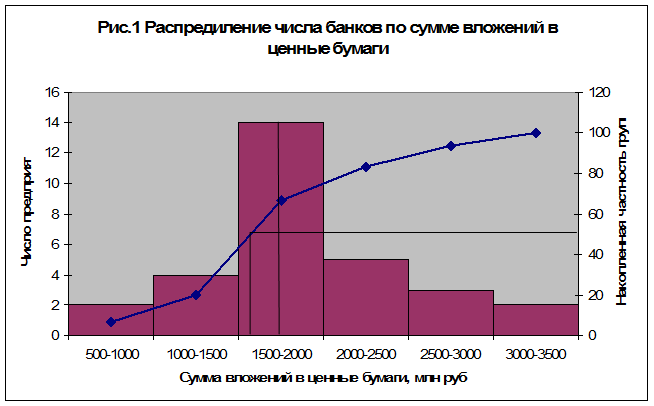
где
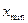 и
и 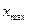 - максимальное и минимальное значения ряда распределения;
- максимальное и минимальное значения ряда распределения;
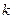 - число групп в группировке (из условия
- число групп в группировке (из условия 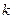 =6).
=6).
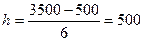
Затем определим нижнюю и верхнюю
интервальные границы для каждой группы:
Интервальный ряд распределения банков по сумме
вложения в ценные
бумаги
Таблица 2
|
диапазон группы
|
число банков в группе
|
Накопленная частность группы, %
|
|
500-1000
|
2
|
6,67
|
|
1000-1500
|
4
|
20
|
|
1500-2000
|
14
|
66,67
|
|
2000-2500
|
5
|
83,33
|
|
2500-3000
|
3
|
93,33
|
|
3000-3500
|
2
|
100
|
|
Итого
|
30
|
|
2. Построим графики полученного ряда распределения. Графически определим
значения моды и медианы.
Мода (М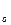 ) это такое
значение, которое соответствует максимальной ординате эмпирической кривой
распределения.
) это такое
значение, которое соответствует максимальной ординате эмпирической кривой
распределения.
Исходя из диаграммы
Мо = 1750 млн. руб.
Медиана (Ме) серединное значение ранжированного ряда вариантов
значений признака.
Исходя из диаграммы
Ме = 1600 млн. руб.
3. Для расчета показателей
вариации построим вспомогательную таблицу:
Таблица 3
|

|
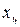
|
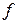
|
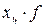
|
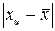
|
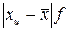
|
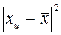
|
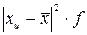
|
|
500-1000
|
750
|
2
|
1500
|
1150
|
2300
|
1322500
|
2645000
|
|
1000-1500
|
1250
|
4
|
5000
|
650
|
2600
|
422500
|
1690000
|
|
1500-2000
|
1750
|
14
|
24500
|
150
|
2100
|
22500
|
315000
|
|
2000-2500
|
2250
|
5
|
11250
|
350
|
1750
|
122500
|
612500
|
|
2500-3000
|
2750
|
3
|
8250
|
850
|
2550
|
722500
|
2167500
|
|
3000-3500
|
3250
|
2
|
6500
|
1350
|
2700
|
1822500
|
3645000
|
|
ИТОГО
|
Х
|
30
|
57000
|
Х
|
14000
|
Х
|
11075000
|
а)
Средняя арифметическая для интервального ряда
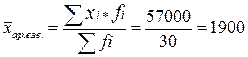 млн. руб.
млн. руб.
б)
Среднее квадратическое отклонение
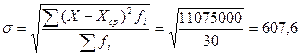 млн руб.
млн руб.
в)
Коэффициент вариации
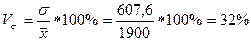
Вывод: анализ полученных данных говорит о том, что сумма
вложений в ценные бумаги в каждом из рассматриваемых банках в среднем отличается
от средней суммы вложения на 607,6 млн.руб.
Значение коэффициента вариации равное 32%
не превышает 33%, а следовательно вариация сумм вложений в ценные бумаги не
велика, а найденная средняя величина
вложения в ценные бумаги равная 1900 млн.руб. может представлять всю
исследуемую совокупность и является ее типичной надежной характеристикой, а вся
совокупность банков может считаться однородной по сумме вложения в ценные
бумаги.
Рассчитаем моду и медиану интервального
ряда распределения.
Мода
(М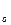 ) – наиболее часто встречающееся значение признака.
) – наиболее часто встречающееся значение признака.
Мода для интервального ряда распределения
с равными интервалами определяется по формуле:
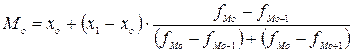 ,
,
где
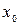 - нижняя граница модального интервала;
- нижняя граница модального интервала;
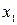 - верхняя граница модального интервала;
- верхняя граница модального интервала;
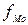 - частота модального интервала;
- частота модального интервала;
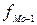 - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному;
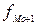 - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.
Первоначально по наибольшей частоте
признака определим модальный интервал. Наибольшее число банков в группе – 14 – сумма
вложений в ценные бумаги в интервале 1500-2000 млн.руб., который и является
модальным.
Подставляем данные в формулу:
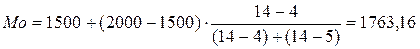 млн.руб.
млн.руб.
Из расчета видно, что наиболее часто
встречающимся значением суммы вложений в ценные бумаги, равно 1763,16 млн руб.
Медиана
(Ме) – значение признака, приходящееся на середину ранжированного ряда.
Медиана для интервального ряда
распределения с равными интервалами определяется по следующей формуле:
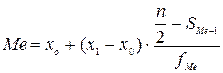 ,
,
где
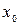 - нижняя граница медианного интервала;
- нижняя граница медианного интервала;
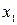 - верхняя граница медианного интервала;
- верхняя граница медианного интервала;
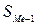 - накопленная частота интервала, предшествующего медианному;
- накопленная частота интервала, предшествующего медианному;
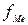 - частота медианного интервала.
- частота медианного интервала.
Определяем медианный интервал, в котором
находится порядковый номер медианы. Для этого подсчитаем сумму частот
накопленным итогом до числа, превышающего половину объема совокупности
(30/2=15). Полученные данные заносим в таблицу 4.
Таблица 4
|
Выручка от продажи продукции, млн.руб.

|
Число предприятий, ед.
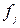
|
Накопленные частоты
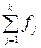
|
|
500-1000
1000-1500
1500-2000
|
2
4
14
|
2<15
6<15
20>15
|
|
2000-2500
2500-3000
3000-3500
|
5
3
2
|
25>15
28>15
30>15
|
|
ИТОГО
|
30
|
|
Медианный интервал: 1500-2000; т.к.
накопленная частота именно в этом интервале впервые превысила величину, равную
половине объема ряда распределения (15).
Подставим
данные в формулу:
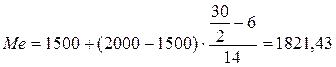 млн.руб.
млн.руб.
Т.о., половина банков имеют сумму вложения
в ценные бумаги до 1821,43 млн.руб., а у другой половины выше 1821,43 млн.руб.
4. Вычислим среднюю арифметическую по исходным данным:
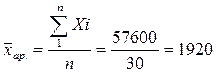 млн.руб.
млн.руб.
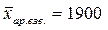 млн.руб.
млн.руб.
Средняя
арифметическая простая применяется тогда, когда имеются несгруппированные
индивидуальные значения признака, т.е. она показывает среднее значение.
При
расчете средней арифметической в интервальных рядах распределения принимаются
середины интервалов, в результате образуется дискретный ряд, т.е. делается
предположение о равномерности, распределения единиц признака внутри группы.
Однако ошибка будет тем меньше, чем уже интервал и чем больше единиц в
интервале.
Более точное значение 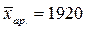 млн.руб., т.к. это
значение рассчитывается по всей совокупности данных.
млн.руб., т.к. это
значение рассчитывается по всей совокупности данных.
ЗАДАНИЕ 2
По исходным данным:
1.
Установите наличие и характер связи между признаками – вложения в ценные бумаги и
прибыль методами:
а)
аналитической группировки;
б) корреляционной таблицы.
2. Измерьте тесноту корреляционной связи
между названными признаками с использованием коэффициентов детерминации и
эмпирического корреляционного отношения.
Сделайте выводы по результатам выполнения
задания.
1. Установим
наличие и характер связи между признаками методами:
а) аналитической группировки:
Составим вспомогательную таблицу для
построения аналитической группировки:
Таблица 5
|
№ гр
|
Группы банков по сумме вложений в ценные бумаги
|
№ банка
|
Сумма вложения в ценные бумаги,
млн. руб., x
|
Прибыль,
млн. руб., y
|
|
1
|
2
|
3
|
4
|
5
|
|
1
|
500-1000
|
10
|
500
|
100
|
|
16
|
700
|
132
|
|
Итого
|
2
|
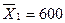
|
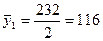
|
|
2
|
1000-1500
|
15
|
1050
|
139
|
|
11
|
1100
|
137
|
|
9
|
1200
|
125
|
|
4
|
1450
|
159
|
|
Итого
|
4
|
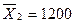
|
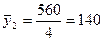
|
|
3
|
1500-2000
|
1
|
1550
|
110
|
|
28
|
1580
|
141
|
|
5
|
1620
|
140
|
|
8
|
1640
|
169
|
|
25
|
1690
|
179
|
|
14
|
1700
|
170
|
|
23
|
1720
|
118
|
|
6
|
1750
|
156
|
|
17
|
1800
|
172
|
|
20
|
1860
|
168
|
|
7
|
1900
|
176
|
|
2
|
1910
|
174
|
|
18
|
1940
|
175
|
|
3
|
1980
|
164
|
|
Итого
|
14
|
 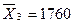
|
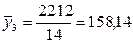
|
|
4
|
2000-2500
|
21
|
2200
|
180
|
|
27
|
2300
|
166
|
|
19
|
2380
|
208
|
|
12
|
2480
|
196
|
|
22
|
2490
|
200
|
|
Итого
|
5
|
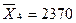
|
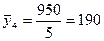
|
|
5
|
2500-3000
|
13
|
2610
|
227
|
|
30
|
2800
|
222
|
|
24
|
2900
|
217
|
|
1
|
2
|
3
|
4
|
5
|
|
Итого
|
3
|
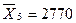
|
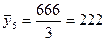
|
|
6
|
3000-3500
|
26
|
3300
|
270
|
|
29
|
3500
|
210
|
|
Итого
|
2
|
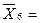 3400 3400
|
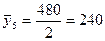
|
|
Всего
|
30
|
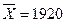
|

|
Построим
теперь аналитическую группировку:
Зависимость прибыли от суммы вложения в ценные бумаги в
различных банках
Таблица 6
|
№ группы
|
Суммы вложения в ценные бумаги, млн. руб., 
|
Средняя сумма вложения в ценные бумаги, млн. руб., 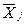
|
Число банков, ед., 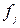
|
Средняя прибыль, млн. руб., 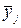
|
|
1
|
500-1000
|
600
|
2
|
116
|
|
2
|
1000-1500
|
1200
|
4
|
140
|
|
3
|
1500-2000
|
1760
|
14
|
158,14
|
|
4
|
2000-2500
|
2370
|
5
|
190
|
|
5
|
2500-3000
|
2770
|
3
|
222
|
|
6
|
3000-3500
|
3400
|
2
|
240
|
|
Итого
|
1920
|
30
|
170
|
Вывод: на основании данных построенной аналитической группировки можно
сказать, что с увеличением суммы вложения банками в ценные бумаги средняя
прибыль банков также увеличивается, что свидетельствует о наличии прямой связи
между указанными признаками.
б) Сначала строим другой интервальный ряд
распределения, где у - прибыль.
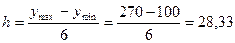
Таблица 7
|
Прибыль, млн.руб., у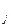
|
Число банков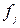
|
|
100-128,33
|
2
|
|
128,33-156,66
|
4
|
|
156,66-184,99
|
14
|
|
184,99-213,32
|
5
|
|
213,32-241,65
|
3
|
|
241,65-270
|
2
|
|
ИТОГО
|
30
|
Корреляционная таблица, характеризующая наличие связи
между выручкой от продажи продукции и чистой прибылью
Таблица 8
|
Сумма вложе-ний в
ценные бумаги, млн руб
|
Прибыль, млн.руб.
|
Итого
|
|
100-128,33
|
128,33-156,66
|
156,66-184,99
|
184,99-213,32
|
213,32-241,65
|
241,65-270
|
|
500-1000
|
1
|
1
|
|
|
|
|
2
|
|
1000-1500
|
|
3
|
1
|
|
|
|
4
|
|
1500-2000
|
2
|
3
|
9
|
|
|
|
14
|
|
2000-2500
|
|
|
2
|
3
|
|
|
5
|
|
2500-3000
|
|
|
|
|
3
|
|
3
|
|
3000-3500
|
|
|
|
1
|
|
1
|
1
|
|
Итого
|
3
|
7
|
12
|
4
|
3
|
1
|
30
|
Вывод: на основании данных построенной
корреляционной таблицы можно сказать, что с увеличением вложений в ценные
бумаги, в преобладающем большинстве случаев, прибыль также увеличивается, что
свидетельствует о наличии прямой корреляционной связи между указанными
признаками.
2. Измерим
тесноту корреляционной связи между названными признаками с использованием
коэффициентов детерминации и эмпирического корреляционного отношения.
Эмпирический
коэффициент детерминации (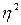 ) определяется как доля межгрупповой дисперсии в общей
дисперсии, характеризует силу влияния факторного (группировочного) признака на
результативный.
) определяется как доля межгрупповой дисперсии в общей
дисперсии, характеризует силу влияния факторного (группировочного) признака на
результативный.
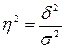
Эмпирическое
корреляционное отношение характеризует тесноту связи; рассчитывается как
корень квадратный из эмпирического коэффициента детерминации.
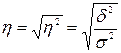
Оба показателя находятся в пределах от 0
до 1. При этом чем ближе показатели к единице, тем связь между изучаемыми
признаками теснее.
0 – связь отсутствует;
1 – связь функциональная.
Для оценки тесноты связи с помощью
корреляционного отношения 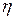 можно воспользоваться
шкалой американского ученого Чеддока:
можно воспользоваться
шкалой американского ученого Чеддока:
0,1-0,3 – связь слабая;
0,3-0,5 – связь умеренная;
0,5-0,7 – связь заметная;
0,7-0,9 – связь тесная;
0,9-0,99 – связь весьма тесная.
Вспомогательная таблица для расчета межгрупповой
дисперсии
Таблица 9
|
№ гр.
|
Сумма вложений в ценные бумаги, млн.руб., 
|
Число банков, ед.,
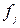
|
Прибыль, млн.руб.
|
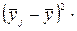 f f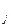
|
|
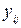
|
в среднем на 1 банк 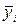
|
|
1
|
500-1000
|
2
|
100;132
|
116
|
5832
|
|
2
|
1000-1500
|
4
|
139;137;125:159
|
140
|
3600
|
|
3
|
1500-2000
|
14
|
110;141;140;169;179;170;118;156;172;168;176;174;175;164
|
158,14
|
1969
|
|
4
|
2000-2500
|
5
|
180;166;208;196;200
|
190
|
2000
|
|
5
|
2500-3000
|
3
|
227;222;217
|
222
|
8112
|
|
6
|
3000-3500
|
2
|
270;210
|
240
|
9800
|
|
ИТОГО
|
30
|
|
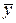 =170 =170
|
31313
|
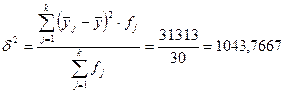
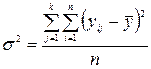 ;
; 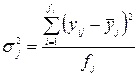 .
.
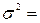 (4900+1444+961+1089+2025+121+3600+841+900+1+81+2704+196+4+4++36+16+25+36+100+16+1444+676+900+3249+2704+2209+10000+1600)/30
= =1395,7333
(4900+1444+961+1089+2025+121+3600+841+900+1+81+2704+196+4+4++36+16+25+36+100+16+1444+676+900+3249+2704+2209+10000+1600)/30
= =1395,7333
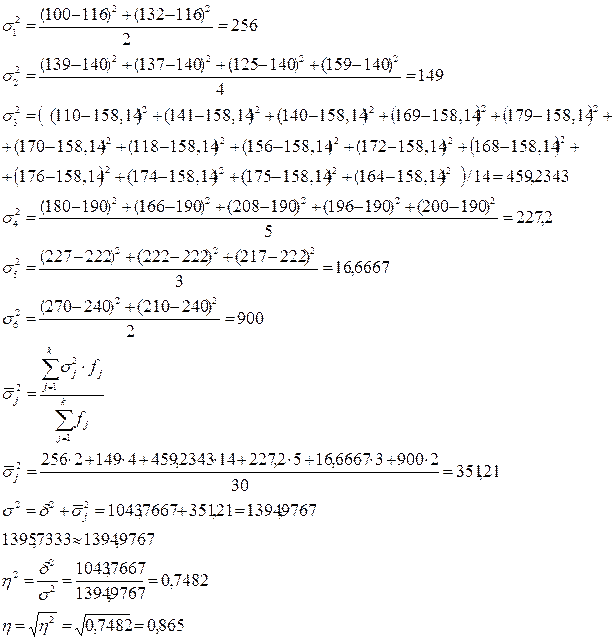
Используя шкалу Чеддока, можно сделать вывод, что связь между суммой
вложения банками в ценные бумаги и
прибылью тесная.
ЗАДАНИЕ 3
По результатам выполнения
задания 1 с вероятностью 0,954 определите:
1.
Ошибку выборки средней величины вложения средств банками в ценные бумаги и
границы, в которых будет находиться средняя величина вложений в генеральной
совокупности.
2. Ошибку выборки доли банков с вложениями
средств в ценные бумаги 2500 и более млн. руб. и границы, в которых будет
находиться генеральная доля.
1. Средняя ошибка выборки для
средней величины признака рассчитывается по следующей формуле:
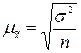
При уровне вероятности Ф(t) = 0,954 коэффициент кратности средней ошибки выборки
t = 2,00.
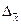 =
=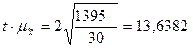 млн.руб.
млн.руб.
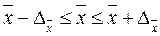
 1886,3618 млн.руб.
1886,3618 млн.руб. 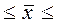 1913,6382 млн.руб.
1913,6382 млн.руб.
С вероятностью 0,954 можно утверждать, что
средняя величина вложения средств банками в ценные бумаги генеральной
совокупности будет находиться в пределах от 1886,3618 млн.руб. до 1913,6382 млн.руб.
2. Доля единиц, обладающих
альтернативной изменчивостью признака:
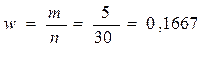
Расчет предельной ошибки выборки для доли
единиц, обладающих альтернативной изменчивостью признака (для повторного
отбора):
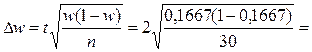 0,1361
0,1361
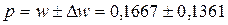
0,0306‹
p ‹ 0,3028
С вероятностью 0,954 можно утверждать, что
доля доли банков с вложениями средств в ценные бумаги 2500 и более млн. руб.
будет находиться в пределах от 0,0306 до 0,3028.
ЗАДАНИЕ 4
По организации имеются
следующие данные, млн.руб.:
Таблица 10
|
Вид продукции
|
Прибыль от продажи продукции, млн руб.
|
Изменение рентабельности в отчетном
периоде по сравнению с базисным (+,-),%
|
|
Базисный период
|
Отчетный период
|
|
А
|
1,0
|
1,4
|
+12
|
|
Б
|
1,2
|
1,0
|
-2
|
|
В
|
0,8
|
1,3
|
+10
|
Определите:
1. Общий
индекс рентабельности реализованной продукции.
2. Абсолютное изменение прибыли от продажи
продукции в результате изменения рентабельности.
Сделайте выводы.
1..
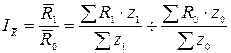
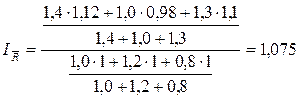
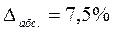
Следовательно, общий прирост рентабельности
отчётного периода по отношению к базисному по всем трём видам продукции
составил 7,5%.
2. Определим абсолютное изменение прибыли от
продажи продукции в результате изменения рентабельности:
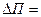 (1,4+1,0+1,3)-(1,0+1,2+0,8)=0,7 млн руб.
(1,4+1,0+1,3)-(1,0+1,2+0,8)=0,7 млн руб.
Вследствие изменения рентабельности производства
всех видов продукции, предприятие
получило на 0,7 млн руб. больше прибыль по сравнению с базисным периодом.
Список используемой литературы:
1. Общая теория
статистики: Учебное пособие./ Лысенко С.Н., Дмитриева И.А., М.: ИД «ФОРУМ»:
ИНФРА-М. 2006. – 208 с.
2. Экономика предприятия
( в схемах, таблицах, расчетах): Учебное пособие / Скляренко В.К., Прудников
В.М., Акуленко Н.Б., Кучеренко А.И., М.: ИНФРА-М, 2006. – 256 с.
3. Статистика: Учеб.
Пособие для вузов. / Гусаров В.М., М.: ЮНИТИ-ДАНА, 2002. – 463 с.