Задача 5. Определите среднюю долю
трудоспособного населения:
Тип населения
|
Регион А
|
Регион
В
|
|
Доля трудоспособного населения, %
|
Численность трудоспособного населения, тыс. чел.
|
Доля трудоспособного населения, %
|
Численность
трудоспособного населения, тыс. чел.
|
|
Городские
|
54,7
|
43,7
|
68,2
|
83,0
|
|
Сельские
|
32,8
|
23,7
|
43,5
|
94,2
|
Решение. По региону А
численность всего городского населения
nг = 43,7 ∙ 100/54,7 = 79,9
численность всего
сельского населения
nс = 23,7 ∙ 100/32,8 = 72,256
а) средняя доля
городского трудоспособного населения по группе регионов А и В
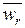= ΣWn / Σn = 54,7 ∙ 79,9 + 68,2 ∙ 83/79,9 + 83 = 61,578
б) средняя доля сельского
трудоспособного населения по группе регионов А и В
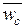= 32,8 ∙ 72,256
+ 43,5 ∙ 94,2/72,256 + 94,2 = 38,855
в) средняя доля
трудоспособного населения региона А
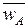= 54,7 ∙ 79,9 +
32,8 ∙ 72,256/79,9 + 72,256 = 44,3
г) средняя доля
трудоспособного населения региона В
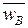= 68,2 ∙ 83 +
43,5 ∙ 94,2/83 + 94,2 = 55,069
д) средняя доля
трудоспособного населения по группе регионов А и В
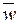= 44,3 ∙ 152,156
+ 55,069 ∙ 177,2/152,156 + 177,2 = 50,094
Задача 11. Распределение
основных фондов по малым предприятиям отрасли характеризуется следующими
данными:
|
Группы предприятий по стоимости
основных фондов, млн. руб.
|
Число предприятий
|
Прибыль в среднем на предприятии,
млн. руб.
|
Групповые дисперсии
|
|
12-27
27-42
42-57
57-72
|
18
40
26
12
|
1,8
3,2
4,8
6,9
|
1,14
1,09
1,69
1,84
|
Рассчитайте коэффициент
детерминации и эмпирическое корреляционное отношение. Сделайте выводы.
Решение. Общая средняя
арифметическая величина
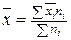= 1/96 ∙ (1,8
∙ 18 + 3,2 ∙ 40 + 4,8
∙ 26 + 6,9 ∙ 12) = 3,833
Средняя из групповых
дисперсий
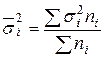= 1/96 ∙ (1,14
∙ 18 + 1,09 ∙ 4, + 1,69 ∙ 26 + 1,84 ∙ 12) = 1,356
Общая средняя квадрата
признака
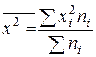= 1/96 ∙ (3,24
∙ 18 + 10,24 ∙ 40 + 23,04 ∙ 26 + 47,61 ∙ 12) = 17,065
Общая дисперсия
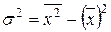= 17,065 – (3,833)2 = 2,373
межгрупповая дисперсия
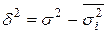= 2,373 – 1,356 = 1,017
Коэффициент детерминации
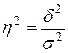= 1,017/2,373 = 0,429
Эмпирическое
корреляционное отношение
η =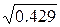 
= 0,655
Доля вариации
результативного признака зависит от стоимости основных фондов на уровне η
= 0,655 по общей шкале 0 ≤ η ≤ 1.
Задача 19. Для
установления среднего размера семья в районе А с числом семей 3 тыс. методом
случайного бесповторного отбора было проведено обследование 70 семей. В
результате обследования получены следующие данные:
|
Размер семей (чел.)
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
Число семей
|
12
|
14
|
16
|
18
|
4
|
3
|
2
|
1
|
Определите: 1) средний
размер семьи; 2) показатели вариации размера семьи: размах вариации, среднее
линейное отклонение, дисперсию, среднее квадратическое отклонение и коэффициент
вариации; 3) с вероятностью 0,954 пределы, в которых изменяется средний размер
семьи в районе А; 4) долю семей, у которых размер семьи 5 человек и более,
гарантируя результат с вероятностью 0,683.
Решение. 1) Средний
размер семьи
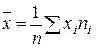= 1/70 ∙ (1
∙ 12 + 2 ∙ 14 + 3 ∙ 16 + 4 ∙ 18 + 5 ∙ 4 + 6
∙ 3 + 7 ∙ 2 + 8 ∙ 1) = 22/7 ≈ 3,1
2) Показатели вариации
размера семьи: размах вариации R = Xmax – Xmin = 8 – 1 = 7
среднее линейное
отклонение
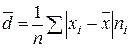= 1 / 70 ∙ (15/7 ∙ 12 + 8/7 ∙ 14 + 1/7
∙ 16 + 6/7 ∙ 18 + 13/7 ∙ 4 + 20/7 ∙ 2 + 34/7 ∙ 1)
= 1,257
дисперсия
σ2 =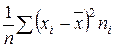 
= 2,6233
среднее квадратическое
отклонение
σ = 1,62
коэффициент
вариации
V =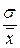 
∙ 100% = 51,5%
3) Доверительный интервал
для среднего размера семьи в районе А
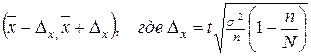= 2
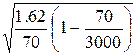= 0,3
с вероятностью 0,954.
С этой вероятностью
средний размер семьи в районе А изменяется в пределах от 2,8 до 3,4.
4) Доля семей, у которых
хi ≥ 5, по данным выборки
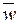= 1/70 ∙ (4 + 3
+ 2 + 1) = 0,143
Доверительный интервал
для соответствующей доли семей в районе А имеет вид
=
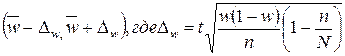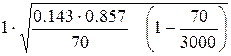= 0,041 (с
вероятностью 0,683).
Доля семей размера свыше
4 человек попадает для района А в пределы от 0,102 до 0,184 с вероятностью
0,683.
Задача 32. Интенсивность
внедрения материалосберегающей технологии характеризуется следующими данными:
|
Технология
|
Базисный период
|
Темпы роста физического объёма
производства, %
|
|
Затраты сырья на 1 изделие, кг
|
Объём производства, шт
|
|
Традиционная
|
43,8
|
432
|
0,67
|
|
Новая
|
27,4
|
568
|
123,5
|
Определите: 1) общий
индекс объёма производства; 2) общий индекс затрат сырья на производство
единицы изделия, если известно, что темп снижения общих затрат сырья составил
6,8%. Сделайте выводы
Решение. 1) Темп роста
0,67 задан в относительных единицах, в процентах это составляет 67%. Объёмы
производства в отчётном периоде составляют
432 ∙ 0,67 = 289
(традиционная технология) и 568 ∙ 123,5/100 = 701 (новая технология).
Общий индекс объёма
производства
Jq =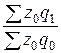 
= 43,8 ∙ 289 + 27,4 ∙ 701 / 43,8 ∙ 432 +
27,4 ∙ 568 = 0,924
2) По условию задачи
общие запасы сырья ΣZ0 q0 базисного периода
сократились до значения ΣZ1 q1 отчётного периода
так, что
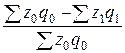= 0,068
Отсюда следует, что
индекс общих затрат сырья на производство единицы изделия
J =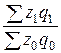 
= 1 – 0,068 = 0,932
Так как для общего
индекса затрат сырья на производство единицы изделия Jz будет
Jz = Jq ∙ Jz,
то Jz =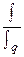
= 0,932/0,924 = 1,009
Хотя общий объём
производства и общие затраты сырья сохранились, общие затраты сырья на
производство единицы изделия даже немного возросли.
Задача 39. Имеются данные
о стоимости медицинского страхования туристов, выезжающих на отдых:
Страна выезда
|
Число страховых полисов, тыс.
|
Стоимость страхового полиса, дол.
|
|
Год
|
|
базисный
|
отчётный
|
базисный
|
отчётный
|
|
страны Европы
|
21,6
|
21,0
|
14,5
|
9,9
|
|
страны Америки
|
3,8
|
1,5
|
15,9
|
17,9
|
|
страны Азии
|
6,3
|
7,4
|
12,0
|
11,7
|
|
|
|
|
|
|
Определите индексы
стоимости переменного, постоянного составов и структурных сдвигов.
Решение. Индекс стоимости
переменного состава:
= 
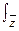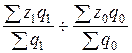= 9,9 ∙ 21 + 17,9 ∙ 1,5 + 11,7 ∙ 7,4 / 21 +
1,5 + 7,4 : 14,5 ∙ 21,6 + 15,9 ∙ 3,8 + 12 ∙ 6,3 / 21,6 + 3,8
+ 6,3 = 0,758
Индекс стоимости
постоянного состава:
=
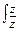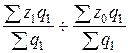= 321,33 / 14,5
∙ 21 + 15,9 ∙ 1,5 + 12 ∙ 7,4 = 0,77
Индекс структурных
сдвигов равен дроби
=
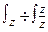0,984.
Задача 47. Динамика
жилищного строительства в регионе характеризуется следующими данными:
|
Показатель
|
1999
|
2001
|
|
Число построенных квартир (тыс.),
всего
|
689
|
692
|
|
В том числе за счёт предприятий и
организаций
|
611
|
602
|
|
Населением за свой счёт и с помощью
кредита
|
78
|
90
|
Для каждого показателя
определите среднегодовой темп прироста (снижения), проведите сравнительный
анализ.
Решение. В таблице
отсутствуют данные за 2000 год. Но для вычисления среднегодовых темпов прироста
(снижения) они не нужны, так как
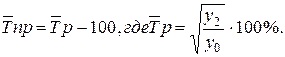
Для указанных трёх
показателей получаем соответствующие значения:
0,2%; - 0,7%; 7,4%.
Сравнительный анализ
результатов: несмотря на значительный темп прироста числа квартир, построенных
населением за свой счёт и с помощью кредита, темп прироста числа построенных
квартир оказался невысоким по причине снижения числа квартир, построенных
предприятиями и организациями.