Министерство
образования и науки РФ
Федеральное
агентство по образованию ГОУ ВПО
Всероссийский
заочный финансово-экономический институт
Кафедра СТАТИСТИКИ
КОНТРОЛЬНАЯ РАБОТА
по дисциплине: «Статистика»
Вариант 3
Преподаватель
Заведующий кафедрой
Галина Павловна Кожевникова
Профессор, доктор физико-математических наук
Москва 2007 г.
ЗАДАНИЕ
Задание 1
По исходным данным (млн. руб.):
|
№ предприятия п/п
|
Среднегодовая стоимость материальных
оборотных фондов
|
Выпуск продукции
|
№ предприятия п/п
|
Среднегодовая стоимость материальных
оборотных фондов
|
Выпуск продукции
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
18,20
|
26,00
|
16
|
11,00
|
15,20
|
|
2
|
14,00
|
16,00
|
17
|
21,80
|
44,90
|
|
3
|
10,00
|
15,00
|
18
|
24,70
|
47,20
|
|
4
|
20,30
|
41,20
|
19
|
19,60
|
39,10
|
|
5
|
23,80
|
40,80
|
20
|
27,90
|
57,00
|
|
6
|
27,50
|
50,80
|
21
|
21,50
|
44,50
|
|
7
|
24,50
|
42,70
|
22
|
19,40
|
38,40
|
|
8
|
20,70
|
44,30
|
23
|
17,00
|
29,50
|
|
9
|
19,20
|
36,00
|
24
|
29,90
|
65,00
|
|
10
|
16,80
|
25,20
|
25
|
25,30
|
54,00
|
|
11
|
12,00
|
23,80
|
26
|
18,80
|
26,40
|
|
12
|
21,70
|
44,80
|
27
|
16,20
|
25,30
|
|
13
|
25,80
|
54,40
|
28
|
18,40
|
26,20
|
|
14
|
27,20
|
63,00
|
29
|
25,90
|
54,90
|
|
15
|
20,40
|
44,20
|
30
|
30,00
|
64,20
|
1. Постройте статистический ряд
распределения организаций (предприятий) по признаку среднегодовая стоимость
материальных оборотных фондов, образовав 5 групп с равными интервалами.
2. Постройте графики полученного ряда
распределения. Графически определите значение моды и медианы.
3.
Рассчитайте характеристики интервального ряда распределения: среднюю
арифметическую, среднее квадратическое отклонение, коэффициент вариации, моду и
медиану.
4. Вычислите среднюю арифметическую по
исходным данным, сравните ее с аналогичным показателем, рассчитанным в п.3 для
интервального ряда распределения. Объясните причину их расхождения.
Сделайте вывод по результатам выполнения
задания.
Задание 2
По исходным данным, приведенным в задании 1:
1. Установите наличие и характер связи
между признаками среднегодовая стоимость материальных оборотных фондов и
выпуск продукции, образовав заданное одинаковое число групп по обоим
признакам с равными интервалами, методами:
а) аналитической группировки;
б) корреляционной таблицы.
2. Измерьте тесноту корреляционной связи
между названными признаками с использованием коэффициента детерминации и
эмпирического корреляционного отношения.
Сделайте вывод по результатам выполнения
задания.
Задание 3
По результатам выполнения задания 1 с
вероятностью 0,954 определите:
1. Ошибку выборки средней стоимости материальных
оборотных фондов и границы, в которых будет находиться средняя стоимость материальных
оборотных фондов в генеральной совокупности.
2. Ошибку выборки доли предприятий со
среднегодовой стоимостью материальных оборотных фондов 22,0 и более млн. руб. и
границы, в которых будет находиться генеральная доля.
Задание 4
Имеются отчетные данные по фирме, тыс.
руб.:
|
Остаток
оборотных средств на начало месяца
|
|
1.01
|
1.02
|
1.03
|
1.04
|
1.05
|
1.06
|
1.07
|
|
200
|
220
|
240
|
220
|
270
|
220
|
230
|
|
Выручка
от продажи продукции
|
|
I квартал
|
II квартал
|
|
3290
|
4160
|
Определите за каждый квартал:
1. Средние остатки оборотных средств
2. Показатели оборачиваемости оборотных
средств:
а) число оборотов;
б) длительность одного оборота.
Результаты расчетов представьте в таблице.
3.
Сумму
оборотных средств, высвобожденных из оборота в результате ускорения их
оборачиваемости.
ВЫПОЛНЕНИЕ
ЗАДАНИЙ
Задание 1
Имеются следующие выборочные данные о
деятельности коммерческих банков за год (выборка 5% -ная механическая), млрд.
руб.:
Таблица № 1.1.
|
№ банка
п/п
|
Пассивы
|
Работающие активы
|
|
1
|
15,0
|
14,6
|
|
2
|
11,0
|
10,0
|
|
3
|
18,6
|
16,8
|
|
4
|
21,0
|
19,4
|
|
5
|
16,0
|
12,0
|
|
6
|
9,0
|
8,0
|
|
7
|
20,4
|
20,2
|
|
8
|
25,0
|
24,0
|
|
9
|
12,0
|
11,0
|
|
10
|
10,0
|
8,0
|
|
11
|
19,3
|
16,9
|
|
12
|
22,0
|
20,9
|
|
13
|
30,0
|
24,5
|
|
14
|
14,0
|
14,4
|
|
15
|
18,0
|
16,5
|
|
16
|
12,0
|
9,5
|
|
17
|
17,5
|
16,6
|
|
18
|
16,5
|
15,2
|
|
19
|
23,0
|
20,1
|
|
20
|
28,0
|
23,5
|
|
21
|
6,0
|
5,0
|
|
22
|
14,0
|
12,5
|
|
23
|
18,5
|
15,8
|
|
24
|
19,2
|
18,8
|
|
25
|
36,0
|
29,0
|
|
26
|
7,0
|
7,0
|
|
27
|
19,4
|
16,5
|
|
28
|
24,0
|
20,6
|
|
29
|
20,6
|
16,8
|
|
30
|
17,0
|
15,9
|
По
исходным данным:
1.
Постройте статистический ряд распределения банков по признаку пассивы,
образовав шесть групп с равными интервалами.
Решение:
Определим
величину равных интервалов.
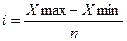 , где n – число образуемых групп
, где n – число образуемых групп
по условию задания 6 групп.
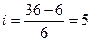 млрд. руб.
млрд. руб.
Тогда
интервалы будут следующими:
6-11
млрд. руб.
11-16
млрд. руб.
16-21
млрд. руб.
22-26
млрд. руб.
26-31
млрд. руб.
31-36
млрд. руб.
На основе исходной таблицы 1.1. группируем
данные по признаку пассивы в шесть групп с интервалом i=5. Результат
группировки отражен в таблице 1.2. «Группировка банков по признаку пассивы»
Таблица 1.2
«Группировка банков по признаку пассивы»
|
№
группы
|
Группы банков по пассивам (млрд. руб.)
|
Число банков
|
Накопленная частота
|
|
1
|
6-11
|
4
|
4
|
|
2
|
11-16
|
6
|
10
|
|
3
|
16-21
|
12
|
22
|
|
4
|
21-26
|
5
|
27
|
|
5
|
26-31
|
2
|
29
|
|
6
|
31-36
|
1
|
30
|
|
Итого:
|
30
|
|
2. С помощью таблицы 1.2 строятся графики
полученного ряда распределения.
На рис. 1.1 и 1.2 изображены следующие
графики: полигон, гистограмма и
кумулята, а также графически определены значение моды и медианы
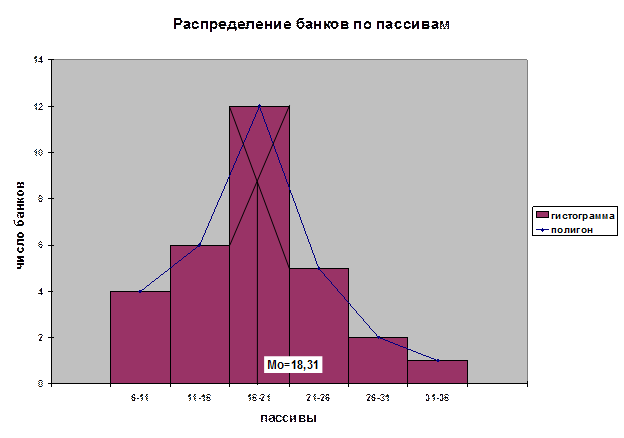 Рис. 1.1
Рис. 1.1
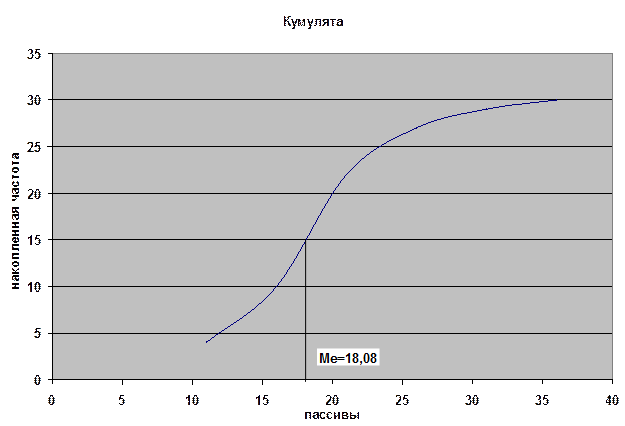
Рис 1.2
4.
Для
расчета вышеуказанных характеристик интервального ряда распределения используем
таблицу 1.2 «Группировка банков по признаку пассивы» и расчетную таблицу 1.3. Сам
расчет приведен в таблице 1.4 «Расчет показателей вариации»
Таблица 1.3
«Расчетная таблица»
|
Группы банков по пассивам (млрд. руб.)
|
число банков (fi)
|
пассивы по группе (Xi') (млрд. руб.)
|
Xi'*fi
|
Xi' - Xср.
|
(Xi' - Xср.)²
|
(Xi' - Xср.)²*fi
|
|
6-11
|
4
|
8,50
|
34,00
|
-9,50
|
90,25
|
361,00
|
|
11-16
|
6
|
13,50
|
81,00
|
-4,50
|
20,25
|
121,50
|
|
16-21
|
12
|
18,50
|
222,00
|
0,50
|
0,25
|
3,00
|
|
21-26
|
5
|
23,50
|
117,50
|
5,50
|
30,25
|
151,25
|
|
26-31
|
2
|
28,50
|
57,00
|
10,50
|
110,25
|
220,50
|
|
31-36
|
1
|
33,50
|
33,50
|
15,50
|
240,25
|
240,25
|
|
Итого:
|
30
|
|
545
|
|
|
1097,5
|
Таблица 1.4
«Расчет показателей вариации»
|
Характеристика
интервального ряда распределения
|
Формула
расчета
|
Расчет
|
|
Средняя арифметическая (млн. руб.)
|
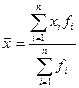
|
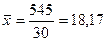
|
|
Среднее квадратическое отклонение
(млн. руб.)
|
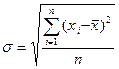
|
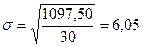
|
|
Коэффициент вариации (%)
|
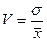
|
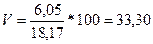
|
|
Мода
(млн. руб.)
|
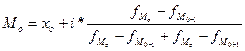
|
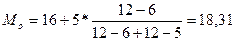
|
|
Медиана
(млн. руб.)
|
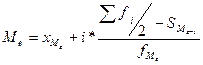
|
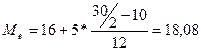
|
где:
fi – частота
повторения индивидуального признака;
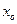 - нижняя граница модального интервала (интервал с наибольшей
частотой);
- нижняя граница модального интервала (интервал с наибольшей
частотой);
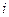 - величина интервала;
- величина интервала;
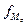 - частота в модальном интервале;
- частота в модальном интервале;
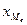 - нижняя граница медианного интервала (накопившего частоту
большую полусуммы всех частот);
- нижняя граница медианного интервала (накопившего частоту
большую полусуммы всех частот);
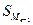 - накопленная частота интервала, предшествующего медианному;
- накопленная частота интервала, предшествующего медианному;
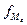 - частота медианного интервала.
- частота медианного интервала.
4. Средняя
арифметическая по исходным данным:
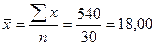 млн. руб.
млн. руб.
Расхождение объясняется тем, что средняя
арифметическая ряда распределения учитывает частоту вхождения каждого значения в
интервал и тем самым дает более точные сведения.
Вывод:
На основании полученной характеристики
интервального ряда коэффициента вариации можно сделать вывод, что колеблемость
признака незначительная, т.к. принадлежит интервалу [0; 40] %, а совокупность
однородна, поскольку коэффициент вариации V= 33,30% < 33%. Наиболее часто встречающиеся значения признака принадлежат модальному
интервалу [16; 21] млн. руб. Полученная медиана Ме=18,08 млн. руб. делит ряд на две равные (по числу единиц)
части – со значениям признака меньше медианы и со значениям признака больше
медианы.
Задание 2
По исходным данным, приведенным в задании 1:
1. а) метод аналитической группировки –
таблица 2.1
Таблица 2.1
«Аналитическая группировка»
|
№ группы
|
Пассивы
по группе (млн. руб.)
|
число банков
|
Работающие активы
|
|
Всего (млн. руб.)
|
в среднем на 1
банк
(млн. руб.)
|
|
1
|
6-11
|
4
|
28,00
|
7,00
|
|
2
|
11-16
|
6
|
72,00
|
12,00
|
|
3
|
16-21
|
12
|
198,00
|
16,50
|
|
4
|
21-26
|
5
|
105,00
|
21,00
|
|
5
|
26-31
|
2
|
48,00
|
24,00
|
|
6
|
31-36
|
1
|
29,00
|
29,00
|
|
|
итого:
|
30
|
480
|
109,5
|
Связь между признаками статистическая,
корреляционная, т.к. в качестве обобщающего параметра взяты средние значения
результативного значения Y (работающие активы), отвечающих одному и тому же X. К
тому же с ростом факторного признака (пассивы) систематически увеличивается
значение средней Yi.
б) метод корреляционной таблицы 2.2
Таблица 2.2
«Корреляционная таблица»
|
Активы
Пассивы
|
Группировка по Y (млн. руб.)
|
|
5-9
|
9-13
|
13-17
|
17-21
|
21-25
|
25-29
|
|
группировка по Х (млн. руб.)
|
6-11
|
4
|
|
|
|
|
|
|
11-16
|
|
4
|
2
|
|
|
|
|
16-21
|
|
1
|
9
|
2
|
|
|
|
21-26
|
|
|
|
4
|
1
|
|
|
26-31
|
|
|
|
|
2
|
|
|
31-36
|
|
|
|
|
|
1
|
|
Итого:
|
4
|
5
|
11
|
6
|
3
|
1
|
Проведя анализ таблицы 2.2 можно сделать
вывод: концентрация частот вдоль диагонали от верхнего левого угла таблицы к
правому нижнему (т.е. большему значению X соответствует большее значение Y) означает
наличие прямой корреляционной связи между признаками.
2. а) коэффициент детерминации:
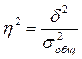 , где
, где 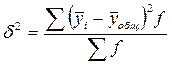 ,
, 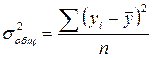
Расчет коэффициента детерминации производится
с использованием данных расчетных таблиц 2.3 и 2.4
Таблица 2.3
«Расчетная таблица»
|
№
группы
|
Пассивы
всего по группе
(млн. руб.)
|
число
пред-
приятий
(f)
|
Работающие активы
|
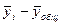
|
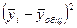
|
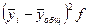
|
|
Всего
(млн. руб.)
|
в среднем на 1
банк
(млн. руб.) (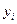 ) )
|
|
1
|
6-11
|
4
|
28,00
|
7,00
|
-9,00
|
81,00
|
324,00
|
|
2
|
11-16
|
6
|
72,00
|
12,00
|
-4,00
|
16,00
|
96,00
|
|
3
|
16-21
|
12
|
198,00
|
16,50
|
0,50
|
0,25
|
3,00
|
|
4
|
21-26
|
5
|
105,00
|
21,00
|
5,00
|
25,00
|
125,00
|
|
5
|
26-31
|
2
|
48,00
|
24,00
|
8,00
|
64,00
|
128,00
|
|
6
|
31-36
|
1
|
29,00
|
29,00
|
13,00
|
169,00
|
169,00
|
|
|
итого:
|
30
|
480
|
109,5
|
|
|
845
|
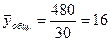 млн. руб.
млн. руб. 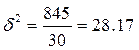
Таблица 2.4
«Расчетная таблица»
|
№
банка
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
Сумма
|
|
Работающие
активы
yi
|
14,60
|
10,00
|
16,80
|
19,40
|
12,00
|
8,00
|
20,20
|
24,00
|
11,00
|
8,00
|
|
|
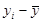
|
-1,40
|
-6,00
|
0,80
|
3,40
|
-4,00
|
-8,00
|
4,20
|
8,00
|
-5,00
|
-8,00
|
|
|
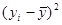
|
1,96
|
36,00
|
0,64
|
11,56
|
16,00
|
64,00
|
17,64
|
64,00
|
25,00
|
64,00
|
300,80
|
|
№
банка
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
|
|
Работающие
активы
yi
|
16,90
|
20,90
|
24,50
|
14,40
|
16,50
|
9,50
|
16,60
|
15,20
|
20,10
|
23,50
|
|
|
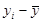
|
0,90
|
4,90
|
8,50
|
-1,60
|
0,50
|
-6,50
|
0,60
|
-0,80
|
4,10
|
7,50
|
|
|
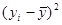
|
0,81
|
24,01
|
72,25
|
2,56
|
0,25
|
42,25
|
0,36
|
0,64
|
16,81
|
56,25
|
216,19
|
|
№
банка
|
21
|
22
|
23
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
|
|
Работающие
активы
yi
|
5,00
|
12,50
|
15,80
|
18,80
|
29,00
|
7,00
|
16,50
|
20,6
|
16,80
|
15,90
|
|
|
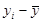
|
-11,00
|
-3,50
|
-0,20
|
2,80
|
13,00
|
-9,00
|
0,50
|
4,60
|
0,80
|
-0,10
|
|
|
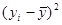
|
121,00
|
12,25
|
0,04
|
7,84
|
169,00
|
81,00
|
0,25
|
21,16
|
0,64
|
0,01
|
413,19
|
|
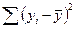
|
930,18
|
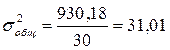 Т.о.
Т.о. 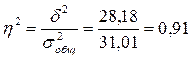 или 91 %
или 91 %
б) эмпирического корреляционного
отношения.
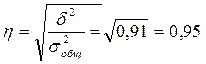
Вывод:
На основании анализа аналитической
группировки и корреляционной таблицы установлена статистическая прямая
корреляционная связь признаков.
Полученный коэффициент детерминации
говорит о том, что изменение выпуска продукции на 91% зависит от изменения
среднегодовой стоимости материальных оборотных фондов и на 9% от остальных
факторов.
В соответствии с оценочной шкалой тесноты
взаимосвязи Чеддока полученное эмпирическое корреляционное отношение η=0,95
входит в интервал [0,9 ; 0,99] , что позволяет сделать вывод о весьма высокой тесноте
связи между двумя рассматриваемыми показателями.
Задание 3
Вычисление ошибок выборки и доверительного интервала для средней и доли
приведено в таблице 3.1
Известно:
вероятность P=0,954 , следовательно t = 2
n = 30 банков
По условию исходные данные являются 5%
механической выборкой из данных за год, т.о. N=(30/5)*100 = 600 банков
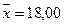 млрд. руб. (из расчетов в задаче 1.4)
млрд. руб. (из расчетов в задаче 1.4)
σ = 6,05 млрд. руб.
(из расчетов в задаче 1.3)
Исходя из данных таблицы 2.3 получаем, что
8 банков имеют пассивы 21,00 и более млрд.
руб. Их доля составляет w = (100/30)*8 = 26,67 %
Таблица 3.1
«Вычисление ошибки выборки и
доверительного интервала»
|
Характеристика
|
Формула
расчета
|
Расчет
|
|
Ошибку выборки средней стоимости материальных оборотных фондов
(млн. руб.)
|
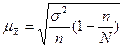
|
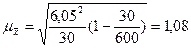
|
|
Предельная
ошибка выборки (млн. руб.)
|
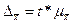
|
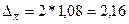
|
|
Доверительные
интервалы для генеральной средней
(млн. руб.)
|
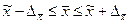
|
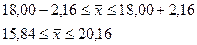
|
|
Ошибку выборки доли
|
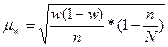
|

|
|
Предельная
ошибка доли (%)
|
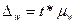
|
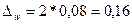 или 16,69 или 16,69
|
|
Доверительные
интервалы для генеральной доли (%)
|
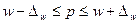
|
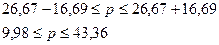
|
Задание 4
1. Для расчета среднего процента изменения прибыли по
коммерческому банку воспользуемся формулой:
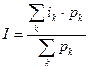 , где
, где
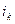 - показатель изменения
прибыли в отчетном периоде k-го филиала по сравнению с базисным;
- показатель изменения
прибыли в отчетном периоде k-го филиала по сравнению с базисным;
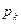 - прибыль в отчетном периоде k-го филиала.
- прибыль в отчетном периоде k-го филиала.
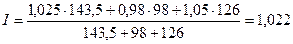 или 102,2%
или 102,2%
Таким образом, средний процент изменения прибыли по коммерческому
банку составил 2,2 %.
2. Для расчета прибыли каждого филиала банка в базисном периоде
воспользуемся формулой 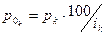 , где
, где
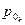 - прибыль в базисном
периоде k-го филиала.
- прибыль в базисном
периоде k-го филиала.
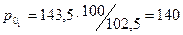 млн.руб.
млн.руб.
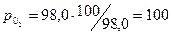 млн.руб
млн.руб
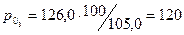 млн.руб.
млн.руб.
Прибыль в базисном периоде 1-го филиала составляла 140 млн.руб;
2-го филиала – 100 млн.руб; 3-го филиала – 120 млн.руб.
Вывод: В целом, по банку,
прибыль в отчетном периоде увеличилась в среднем на 2,2%, несмотря на
то, что показатель изменения прибыли 2-го филиала банка в отчетном периоде
составил -2%