Федеральное агентство по образованию
ГОУ ВПО
Всероссийский заочный финансово-экономический институт
__________________________________________________________________
Кафедра статистики
КОНТРОЛЬНАЯ РАБОТА
по дисциплине
«СТАТИСТИКА»
Вариант № 2
2007
Имеются следующие
выборочные данные об инвестировании предприятиями региона собственных средств в
основные фонды (выборка 10%-ная механическая, млн. руб.:
Таблица 1
|
№ предприя-тия
|
Нераспределен-ная
прибыль
|
Инвестиции в
основные фонды
|
№ предприя-тия
|
Нераспределен-ная
прибыль
|
Инвестиции в
основные фонды
|
|
1
|
2,7
|
0,37
|
14
|
3,9
|
0,58
|
|
2
|
4,8
|
0,90
|
15
|
4,2
|
0,57
|
|
3
|
6,0
|
0,96
|
16
|
5,6
|
0,78
|
|
4
|
4,7
|
0,68
|
17
|
4,5
|
0,65
|
|
5
|
4,4
|
0,60
|
18
|
3,8
|
0,59
|
|
6
|
4,3
|
0,61
|
19
|
2,0
|
0,16
|
|
7
|
5,0
|
0,65
|
20
|
4,8
|
0,72
|
|
8
|
3,4
|
0,51
|
21
|
5,2
|
0,63
|
|
9
|
2,3
|
0,35
|
22
|
2,2
|
0,24
|
|
10
|
4,5
|
0,70
|
23
|
3,6
|
0,45
|
|
11
|
4,7
|
0,80
|
24
|
4,1
|
0,57
|
|
12
|
5,4
|
0,74
|
25
|
3,3
|
0,45
|
|
13
|
5,8
|
0,92
|
|
|
|
ЗАДАНИЕ 1.ИССЛЕДОВАНИЕ СТРУКТУРЫ
СОВОКУПНОСТИ
По исходным данным:
1.
Постройте
статистический ряд распределения предприятий по признаку нераспределенная
прибыль, образовав четыре группы с равными интервалами.
2.
Постройте
графики полученного ряда распределения. Графически определите значение моды и
медианы.
3.
Рассчитайте
характеристики интервального ряда распределения: среднюю арифметическую,
среднее квадратическое отклонение, коэффициент вариации, моду и медиану.
4.
Вычислите
среднюю арифметическую по исходным данным, сравните ее с аналогичным
показателем, рассчитанным для интервального ряда распределения. Объясните
причину их расхождения.
Сделайте выводы по
результатам выполнения задания.
1) Статистический ряд
распределения предприятий по признаку нераспределенная прибыль:
Таблица 2
|
№ группы
|
Нераспределен-ная
прибыль, млн. руб.
x
|
Число предприя-тий,
ед.
f
|
Кумуля-тивное число
предприя-тий, ед.
∑f
|
Нераспреде-ленная
прибыль, млн. руб.
(дискретн.)
x
|
|
1
|
|
|
|
|
|
2
|
|
|
|
|
|
3
|
|
|
|
|
|
4
|
|
|
|
|
|
Итого
|
|
|
|
|
Группировочный признак:
нераспределенная прибыль.
Число групп: четыре.
Определение ширины
интервала: 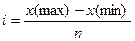 ,где x(max) –максимальное значение признака, x(min) – минимальное значение признака, n – число групп.
,где x(max) –максимальное значение признака, x(min) – минимальное значение признака, n – число групп.
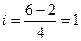
Таблица 3 – Распределение предприятий
по признаку «нераспределенная прибыль»
|
№ группы
|
Нераспределен-ная
прибыль, млн. руб.
x
|
Число предприя-тий,
ед.
f
|
Кумуля-тивное число
предприя-тий, ед.
∑f
|
Нераспреде-ленная
прибыль, млн. руб.
(дискретн.)
x
|
|
1
|
2-3 (-)
|
4
|
4
|
2,5
|
|
2
|
3-4
|
5
|
9
|
3,5
|
|
3
|
4-5
|
10
|
19
|
4,5
|
|
4
|
5-6
|
6
|
25
|
5,5
|
|
Итого
|
|
25
|
|
|
2) Графики распределения признака «нераспределенная прибыль»:
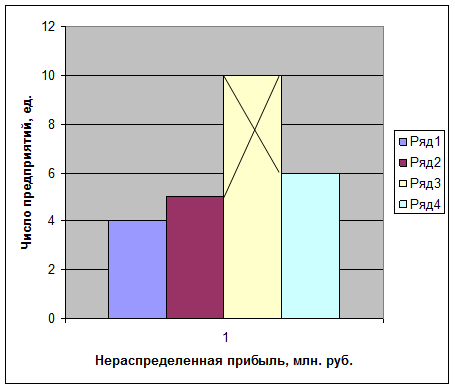
Рис. 1. Интервальный ряд
распределения нераспределенной прибыли
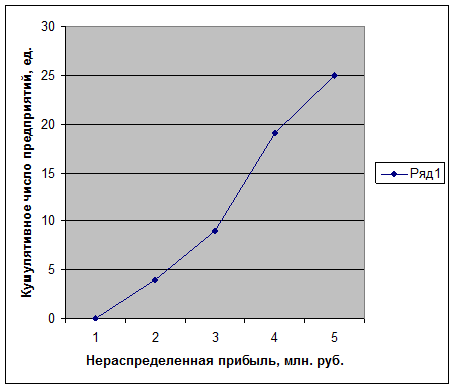
Рис. 2. Кумулята
3)
Таблица 4 – Данные для вычисления
характеристик интервального ряда
|
№ группы
|
Нераспределен-ная
прибыль, млн. руб.
x
|
Число предприя-тий,
ед.
f
|
Нераспреде-ленная
прибыль, млн. руб.
(дискретн.)
x
|
Общая
нераспределен-ная прибыль, млн. руб.
xf
|
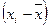
|
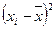
|
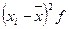
|
|
1
|
2-3 (-)
|
4
|
2,5
|
10
|
-1.72
|
2.958
|
11.83
|
|
2
|
3-4
|
5
|
3,5
|
17.5
|
-0.72
|
0.518
|
2.59
|
|
3
|
4-5
|
10
|
4,5
|
45
|
0.28
|
0.78
|
0.78
|
|
4
|
5-6
|
6
|
5,5
|
33
|
1.28
|
1.638
|
9.83
|
|
Итого
|
|
25
|
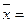 4.22 4.22
|
105.5
|
|
|
25.04
|
1. Средняя арифметическая:
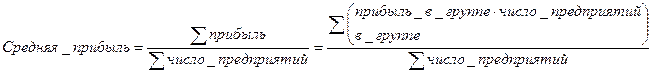
- средняя арифметическая взвешенная.
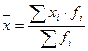 ;
; 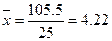 (млн. руб.)
(млн. руб.)
Вывод: значение нераспределенной прибыли в выборке
предприятий в среднем составляет 4,22 млн. руб.
2. Мода:
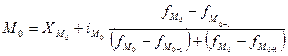
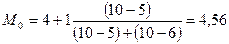 ( млн. руб.)
( млн. руб.)
Вывод: размер нераспределенной прибыли, наиболее часто
встречающийся в данной выборке предприятий, составляет 4,56 млн. руб.
3. Медиана:
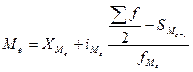
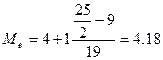
Вывод: 50% предприятий имеют нераспределенную прибыль в
размере менее 4,18 млн. руб., остальные 50% - более 4,18 млн. руб.
4. Среднее квадратическое отклонение:
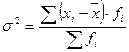
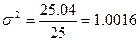
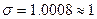 (млн. руб.)
(млн. руб.)
Вывод: в среднем, каждое значение
нераспределенной прибыли предприятий, отличается от 4,22 млн. руб. на 1 млн. руб.
5. Коэффициент вариации:
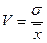
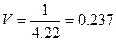 или 23,7%
или 23,7%
Вывод: 23,7% < 40%, следовательно,
вариация нераспределенной прибыли предприятий в данной совокупности невысокая;
совокупность предприятий по признаку «нераспределенная прибыль» количественно
однородна; среднее значение типичное и надежное.
4) Средняя арифметическая (по
исходным данным):
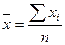
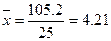 (млн. руб.)
(млн. руб.)
Вывод: средняя арифметическая простая
отличается от средней арифметической взвешенной, так как при расчете последней
делается предположение о нормальности распределения, на практике это может
привести к погрешности в вычислениях.
ЗАДАНИЕ 2. ВЫЯВЛЕНИЕ НАЛИЧИЯ
КОРРЕЛЯЦИОННОЙ СВЯЗИ МЕЖДУ ПРИЗНАКАМИ, УСТАНОВЛЕНИЕ НАПРАВЛЕНИЯ СВЯЗИ И
ИЗМЕРЕНИЕ ЕЕ ТЕСНОТЫ.
По
исходным данным:
1. Установить наличие и характер связи
между признаками «нераспределенная прибыль» и «инвестиции в основные фонды»,
образовав заданное одинаковое число групп по обоим признакам с равными интервалами,
методами:
а) аналитической
группировки;
б) корреляционной
таблицы.
2. Измерить тесноту
корреляционной связи между названными признаками с использованием коэффициента
детерминации и эмпирического корреляционного отношения.
1) Аналитическая группировка.
Таблица 5
|
№ группы
|
Нераспределен-
ная прибыль,
млн. руб.
x
|
Число предприя-
тий, ед.
f
|
Среднее значение
инвестиций в основные фонды, млн. руб.
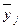
|
|
1
|
|
|
|
|
2
|
|
|
|
|
3
|
|
|
|
|
4
|
|
|
|
|
Итого
|
|
|
|
Таблица 5а – Распределение
предприятий по величине нераспределенной прибыли и среднему значению инвестиций
в основные фонды
|
№ группы
|
Нераспределен-
ная прибыль,
млн. руб.
x
|
Число предприя-
тий, ед.
f
|
Среднее значение
инвестиций в основные фонды, млн. руб.
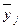
|
|
1
|
2-3 (-)
|
4
|
0,280
|
|
2
|
3-4
|
5
|
0,516
|
|
3
|
4-5
|
10
|
0,680
|
|
4
|
5-6
|
6
|
0,780
|
|
Итого
|
|
25
|
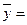 0,607 0,607
|
Средняя арифметическая:
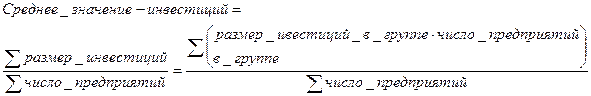
- средняя арифметическая взвешенная.
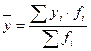 ;
; 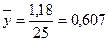 (млн. руб.)
(млн. руб.)
Вывод: среднее значение инвестиций в основные фонды
составляет 0,607 млн. руб.
Вывод. Связь между
признаками прямая: при увеличении размера нераспределенной прибыли предприятий
инвестирование средств в основные фонды увеличивается.
Корреляционная таблица.
Таблица 6 –
Распределение предприятий по величине нераспределенной прибыли и инвестициям в
основные фонды
|
Нераспределенная
прибыль,
млн. руб.
|
Инвестиции в
основные фонды, млн. руб.
|
|
0,16 – 0,36
(-)
|
0,36 – 0,56
|
0,56 – 0,76
|
0,76 – 0,96
|
Итого
|
|
2 – 3 (-)
|
3
|
1
|
|
|
4
|
|
3 – 4
|
|
3
|
2
|
|
5
|
|
4 – 5
|
|
|
8
|
2
|
10
|
|
5 - 6
|
|
|
3
|
3
|
6
|
|
Итого
|
3
|
4
|
13
|
5
|
25
|
Вывод. Связь между
признаками прямая: при увеличении размера нераспределенной прибыли предприятий
инвестирование средств в основные фонды увеличивается.
2)
Таблица 7 – Данные для решения задачи
|
№ группы
|
x
|
f
|
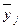
|
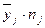
|
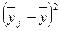
|
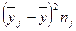
|
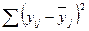
|
|
1
|
2-3 (-)
|
4
|
0,280
|
1,12
|
0,1069
|
0,428
|
0,029
|
|
2
|
3-4
|
5
|
0,516
|
2,58
|
0,0083
|
0,041
|
0,0183
|
|
3
|
4-5
|
10
|
0,680
|
6,8
|
0,0053
|
0,053
|
0,1012
|
|
4
|
5-6
|
6
|
0,780
|
4,86
|
0,0299
|
0,180
|
0,093
|
|
Итого
|
|
25
|
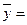 0,607 0,607
|
|
0,1505
|
0,702
|
0,2415
|
Эмпирический коэффициент
детерминации: 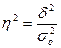
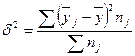 ;
; 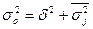 ;
; 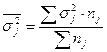 ;
; 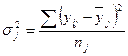
Межгрупповая дисперсия:
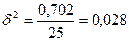 - характеризует
вариацию размера инвестиций в основные фонды под влиянием фактора
«нераспределенная прибыль».
- характеризует
вариацию размера инвестиций в основные фонды под влиянием фактора
«нераспределенная прибыль».
Расчет внутригрупповых дисперсий:
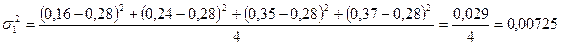
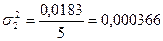 ;
; 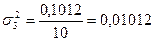 ;
; 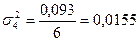
Средняя из внутригрупповых дисперсий:
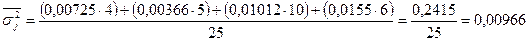 - характеризует
вариацию размера инвестиций в основные фонды, которая возникает под влиянием
всех других признаков, кроме признака «нераспределенная прибыль».
- характеризует
вариацию размера инвестиций в основные фонды, которая возникает под влиянием
всех других признаков, кроме признака «нераспределенная прибыль».
Общая дисперсия:
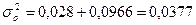 - характеризует всю
вариацию результативного признака «инвестиции в основные фонды» и зависящую от
фактора «нераспределенная прибыль», и зависящую от других факторов, неучтенных
при построении группировки.
- характеризует всю
вариацию результативного признака «инвестиции в основные фонды» и зависящую от
фактора «нераспределенная прибыль», и зависящую от других факторов, неучтенных
при построении группировки.
Эмпирический коэффициент
детерминации:
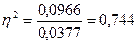 или 74,4%
или 74,4%
Вывод: 74,4% вариации размера
инвестиций в основные фонды вызывает значение нераспределенной прибыли,
остальные 25,6% вариации вызывают другие неучтенные факторы.
Эмпирическое корреляционное
отношение:
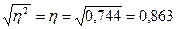 - связь между
признаками «нераспределенная прибыль» и «инвестиции в основные фонды» тесная.
- связь между
признаками «нераспределенная прибыль» и «инвестиции в основные фонды» тесная.
ЗАДАНИЕ 3
По
результатам выполнения задания 1 с вероятностью 0,954 определить:
1. Ошибку выборки среднего размера
нераспределенной прибыли и границы, в которых будет находиться средний размер
нераспределенной прибыли в генеральной
совокупности.
2. Ошибку выборки доли предприятий с
нераспределенной прибылью 5,0 и более млн. руб. и границы, в которых будет
находиться генеральная доли.
Решение:
1) 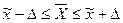
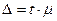 ;
; 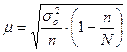 (выборка
механическая, бесповторная)
(выборка
механическая, бесповторная)
t = 2 (при р
= 0,954) 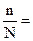 0,1 (выборка 10%-ная)
0,1 (выборка 10%-ная) 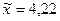 (млн. руб.)
(млн. руб.)
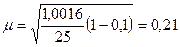
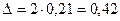
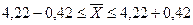
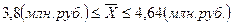
Вывод: с вероятностью 0,954 можно
гарантировать, что средний размер нераспределенной прибыли в генеральной
совокупности находится в пределах от 3,8 млн. руб. до 4,64 млн. руб.
2)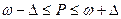
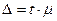 ;
; 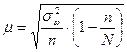 (выборка
механическая, бесповторная)
(выборка
механическая, бесповторная)
Доля предприятий с нераспределенной
прибылью 5,0 и более млн. руб. составляет: 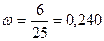 или 24,0% предприятий
нераспределенной прибылью 5,0 и более млн. руб.
или 24,0% предприятий
нераспределенной прибылью 5,0 и более млн. руб.
Дисперсия доли предприятий с
нераспределенной прибылью 5,0 и более млн. руб.: 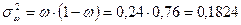
t = 2
( при р = 0,954) 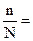 0,1 ( выборка 10%-ная)
0,1 ( выборка 10%-ная)
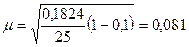
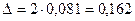
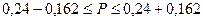
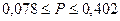 или 7,8 % ≤ Р
≤ 40,2%
или 7,8 % ≤ Р
≤ 40,2%
Вывод: с вероятностью 0,954 можно
гарантировать, что доля предприятий с нераспределенной прибылью 5,0 и более
млн. руб. в генеральной совокупности находится в пределах от 7,8 % до 40,2 %.
ЗАДАНИЕ 4
Динамика
инвестиций в промышленности региона характеризуется следующими данными:
Таблица 8
|
Год
|
Инвестиции, млн. руб.
|
По сравнению с предыдущим годом
|
Абсолютное значение 1%
прироста, млн. руб.
|
|
Абсолютный прирост, млн. руб.
|
Темп роста, %
|
Темп прироста, %
|
|
1
|
|
|
|
|
|
|
2
|
|
|
102
|
|
15
|
|
3
|
|
40,0
|
|
|
|
|
4
|
|
|
|
3
|
|
|
5
|
|
56,9
|
|
|
|
Определить:
1. Инвестиции за каждый год.
2. Недостающие показатели анализа ряда
динамики и внести их в таблицу.
3. Средний темп роста и прироста.
4. Осуществить прогноз размера
инвестиций на следующие два года на основе найденного среднегодового темпа
роста.
Решение:
Таблица 9 – Показатели анализа ряда
динамики
|
Год
|
Инвестиции, млн.
руб.
у
|
По сравнению с
предыдущим годом
|
Абсолютное значение
1% прироста, млн. руб.
|
|
Абсолютный прирост,
млн. руб.
|
Темп роста, %
|
Темп прироста, %
|
|
1
|
1500,0
|
-
|
|
|
|
|
2
|
1530,0
|
30,0
|
102
|
2
|
15
|
|
3
|
1570,0
|
40,0
|
102,6
|
2,6
|
15,3
|
|
4
|
1617,1
|
47,1
|
103
|
3
|
15,7
|
|
5
|
1674,0
|
56,9
|
103,5
|
3,5
|
16,17
|
Абсолютный прирост: 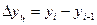
Темп роста: 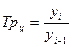
Темп прироста: 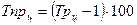
Абсолютное значение 1% прироста: 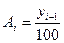
Дано: 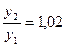 ;
; 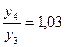 ;
; 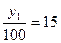 ;
; 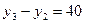 ;
; 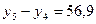
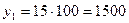
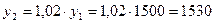
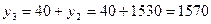
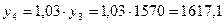
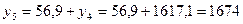
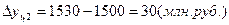 ;
; 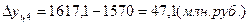
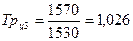 ;
; 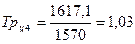 ;
; 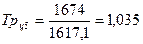
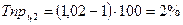 ;
; 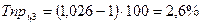 ;
; 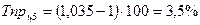
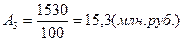 ;
; 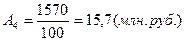 ;
;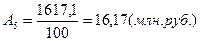
Средний темп роста:
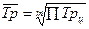
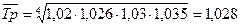
Вывод: в течение пяти лет размер
инвестиций увеличивается в среднем в 1,028 раза за один год.
Средний темп прироста:
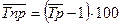
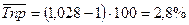
Вывод: в течение пяти лет размер
инвестиций в среднем увеличивается на 2,8% за один год.
Прогноз на следующие два года.
Тенденцию можно считать
показательной, так как цепные темпы роста примерно одинаковы. 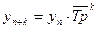
k = 1, 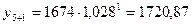 ;
;
k = 2, 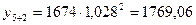
Вывод: в шестом году размер
инвестиций составит 1720,87 млн. руб.; в седьмом году – 1769,06 млн. руб.
Список литературы
1. Гусаров В. М. Теория статистики:
Учебное пособие для вузов. – М.: Аудит, ЮНИТИ, 1998.
2. Статистика финансов: Учебник /Под
ред. В. Н. Салина. -М.: Финансы и статистика, 2000.
3. Статистика: Учебник /Под ред. В.С.
Мхитаряна. -М.: Экономистъ, 2005.