Всероссийский заочный
финансово-экономический институт
КУРСОВАЯ РАБОТА
ПО ДИСЦИПЛИНЕ
«СТАТИСТИКА»
НА ТЕМУ:
«Статистическое изучение страхового
рынка»
ВАРИАНТ № 20
Исполнитель
Факультет Учетно-статистический
Специальность Бухгалтерский учет, анализ
и аудит
Группа
№ личного дела
Руководитель кандидат экономических наук,
доцент,
Пуляшкин Владимир Васильевич
Москва 2008.
СОДЕРЖАНИЕ
Введение………………………………………………………………………..3
1. Страховой рынок……………………………………………………………....5
1.1. Экономическая сущность страхования;………………………………....5
1.2. Показатели имущественного страхования;……………………………...8
1.3. Показатели статистики личного страхования;…………………………11
1.4. Основные показатели
деятельности страховых организаций…………13
2. Расчетная часть………………………………………………………………..16
2.1. Выполнение задания 1…………………………………………………...16
2.2. Выполнение задания 2…...……….……………………………………...23
2.3. Выполнение задания 3...............................................................................30
2.4. Выполнение задания 4 .......................................................33
Заключение.........................................................................................................35
Список использованной литературы...............................................................36
ВВЕДЕНИЕ.
Страхование в России за очень
короткий исторический срок из государственной монополии превратилось в
динамично развивающуюся коммерческую сферу деятельности. В силу этих
обстоятельств тема «Статистическое изучение страхового рынка» весьма актуальна.
В современных условиях существенно
возросла роль статистического анализа финансово-экономической деятельности при
разработке стратегии управления компанией и принятия управленческих решений.
Целью курсовой работы является
изучение темы «Статистическое изучение страхового рынка» и выполнение
практических заданий на основе пройденного и
изложенного в работе теоретического материала. В теоретической части
работы будет освещена структура страхования, приведены методы расчетов
статистических показателей, применяемых для изучения динамики данного явления,
статистические данные, соответствующие настоящему времени.
В расчётной части курсовой работы
будет построен интервальный ряд распределения, найдены средние характеристики,
мода и медиана полученного интервального ряда распределения путем расчетов и
графическим методом. Будет установлено наличие и характер связи между
признаками методом аналитической группировки, измерена теснота корреляционной связи между признаками с использованием
коэффициентов детерминации и эмпирического корреляционного отношения. Будут определены ошибка выборки для среднего
дохода страховых организаций и границ, в которых будет находиться генеральная
средняя, определена ошибка выборки для доли страховых организаций с заданным
признаком, а также границы, в которых будет находиться генеральная доля.
По данным о деятельности страховых организаций одного из
регионов в отчётном году необходимо выполнить ряд заданий:
Задание 1.
1. Построить
статистический ряд распределения страховых организаций по признаку Доходы, образовав пять
групп с равными интервалами.
2. Рассчитать
характеристики интервального ряда распределения: среднюю арифметическую,
среднее квадратическое отклонение, коэффициент вариации, моду и медиану.
Сделать выводы по результатам
выполнения задания.
Задание 2.
1. Установить наличие и характер связи между
признаками – доходы и прибыль методом аналитической группировки, образовав
пять групп с равными интервалами по факторному признаку.
2.
Измерить тесноту корреляционной связи между названными признаками с использованием
коэффициентов детерминации и эмпирического корелляционного отношения.
Сделать
выводы по результатам выполнения задания.
Задание 3.
По
результатам задания 1 с вероятностью 0,954 определить:
1.Ошибку выборки средней величины
доходов и границы, в которых она будет находиться в генеральной совокупности.
2.Ошибку выборки доли страховых
организаций с доходами 14 млн. руб. и более и границы, в которых будет
находиться генеральная доля.
Задание 4.
Определить тарифную ставку
страхования профессиональной ответственности аудиторов при средней убыточности
55 руб. на 100 руб. страховых сумм, экспертной оценке вероятности наступления
страхового события – 0,05, числе договоров – 1200, доле абсолютной нагрузки в
брутто-ставке – 25% и вероятности непревышения возмещения по сравнению со
страховыми суммами – 0,997.
1. СТРАХОВОЙ РЫНОК
1.1. Экономическая сущность страхования.
Страхование – система экономических отношений,
включающая образование специального фонда (страхового фонда) и его
использование (распределение и перераспределение) для преодоления и возмещения
разного роа потерь, ущерба, вызванных неблагоприятными событиями (страховыми случаями)
путем выплаты возмещения и страховых сумм.
В страховании обязательно наличие двух
сторон: специальной организации, ведающей созданием и использованием
соответствующего фонда, - страховщика и юридических и
физических лиц, вносящих в фонд установленные платежи – страхователей (полисодержателей),
взаимные обязательства которых регламентируются договором страхования в
соответствии с условиями страхования. Страховые организации образуют при этом два
вида страховых резервов: по имущественному страхованию и страхованию от
несчастных случаев; по страхованию жизни, пенсий и медицинскому страхованию.
Они предназначаются для обеспечения страховой защиты страхователей.
Отличительные особенности страхования:
¨ отношения между страховщиком и
страхователем имеют вероятностный характер, т. к. в их основе лежит страховой
риск. Под страховым риском чаще всего понимается вероятность наступления
ущерба жизни, здоровью, имуществу страхователя (застрахованного) в результате страхового случая, т.е. фактически
происшедшего страхового события. За
рубежом широко применяется страхование экономических
рисков: коммерческих, правовых,
политических и рисков в финансово-кредитной сфере. Риск является объективной
предпосылкой возникновения страховых событий; если нет риска – нет и
потребности в страховании. Однако не всякий риск может лечь в основу страховых
отношений. Застрахован может быть только тот риск, по которому можно оценить
вероятность наступления страхового случая, определить размер возможного ущерба
и исчислить эквивалентную страховую сумму;
¨ возвратность средств: все средства,
собранные страховщиком для выплаты страхового возмещения, возвращаются
страхователям, но не каждому в отдельности, а только тем, которые пострадали в
данный момент времени;
¨ раскладка ущерба: общая сумма ущерба, понесенного
страхователями за определенный промежуток времени, раскладывается на всех участников
страхования, причем результат раскладки представляет величину страхового
платежа.
Страховщик
и страхователь вступают во взаимодействие в условиях страхового рынка. Страховой
рынок – это особая социально-экономическая среда, определенная сфера денежных
отношений, где объектом купли-продажи выступает страховая защита, формируется
спрос и предложение на нее. Объективная необходимость развития страхового рынка
– необходимость обеспечения бесперебойного воспроизводственного процесса путем
оказания денежной помощи в случае
непредвиденных неблагоприятных обстоятельств. Страховой рынок можно
рассматривать также, как форму организации денежных отношений по формированию и
распределению страхового фонда для обеспечения страховой защиты общества, как
совокупность страховых организаций, которые принимают участие в оказании
соответствующих услуг.
Обязательное условие существования
страхового рынка – наличие общественной потребности на страховые услуги и
наличие страховщиков, способных удовлетворять эти потребности. В настоящее
время страховой рынок России характеризуется ростом числа страховщиков, а также
объемов совершаемых ими операций, появлением новых потребностей и новых направлений
их деятельности.
Структура страхового рынка может быть
представлена в институциональном и территориальном аспектах:
¨ в институциональном аспекте она представлена акционерными, корпоративными,
взаимными и государственными страховыми компаниями;
¨ в территориальном аспекте можно выделить местный (региональный),
национальный (внутренний) и мировой (внешний) страховые рынки.
Страхование
делится на имущественное, личное страхование, страхование ответственности,
социальное страхование и может быть обязательным и добровольным.
Имущественное страхование – вид страхования,
объектом которого выступают материальные ценности (строения, транспортные
средства, продукция, материалы и др.). Оно осуществляется на случай пожара,
аварий, хищений, порчи и пр.
Личное страхование – вид
страхования, в котором объектом страховых отношений выступают имущественные
интересы, связанные с жизнью, здоровьем, трудоспособностью и пенсионным
обеспечением страхователя.
Страхование ответственности – вид
страхования, объектом которого выступает обязанность страхователей выполнять
какие-либо договорные условия (по поставкам товаров, погашению кредитов и др.)
или обязанность страхователей по возмещению материального ущерба. При
страховании ответственности возмещение ущерба производится страховой компанией.
Социально страхование –
самостоятельный вид страхования с целью материального обеспечения
нетрудоспособных граждан в результате болезни, несчастного случая, рождения
ребенка и других обстоятельств. Социальное страхование может быть
государственным и негосударственным.
Страхование представляет собой
специфический вид деятельности. Оно занимается финансовой стороной таких
явлений и процессов, которые по своей природе вероятностны, т.е. могут
наступить или не наступить, и которые проявляются в массе случаев. Для
управления этими явлениями и процессами необходимо располагать точной и
объективной информацией. Статистика занимается сбором, обработкой и анализом
информации, происходящих в области страховании; выявлением закономерностей
появления страховых событий (против которых осуществляется страхование),
оценкой их частоты, тяжести и опустошительности; установлением тарифных ставок.
Выполнение этих задач требует
применения комплекса статистических методов, проведения специальных
статистических наблюдений.
1.2. Показатели имущественного страхования.
Основу системы
показателей составляют характеристики, получаемые непосредственно из
наблюдения. Применяемые в имущественном страховании показатели делятся на 3
группы:
- абсолютные (объёмные)
показатели
- средние
- относительные.
Основные абсолютные показатели.
|
Обозначение
|
Значение
|
|
Nmax
|
Страховое
поле, максимальное число объектов, которое может быть охвачено страхованием
|
|
N
|
Число застрахованных объектов,
или число заключённых договоров страхования за определенный период (страховой
портфель)
|
|
S
|
Страховая сумма застрахованного
объекта
|
|
V
|
Сумма поступившего страхового
платежа (страховой взнос)
|
|
nС
|
Число страховых случаев
|
|
nП
|
Число пострадавших объектов
|
|
Sп
|
Страховая сумма пострадавших
объектов
|
|
W
|
Сумма выплаченного страхового
возмещения
|
Основные средние показатели.
|
Формула
|
Показатель
|
|
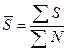
|
Средняя
страховая сумма застрахованного имущества
|
|
|
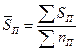
|
Средняя
страховая сумма пострадавших объектов
|
|
|
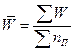
|
Средний
размер выплаченного страхового возмещения
|
|
|
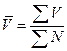
|
Средний
размер страхового взноса
|
|
|
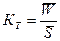
|
Коэффициент
тяжести страховых событий
|
|
|
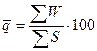 <1 <1
|
Средний
уровень убыточности страховых сумм
|
|
Приведенные показатели используются для характеристики
деятельности страховых организаций и анализа. Они являются основой для
исчисления относительных показателей.
Основные относительные показатели
|
Показатель
|
Формула
расчета
|
Пояснения
|
|
Степень охвата страхового поля
|
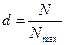
|
Показывает долю застрахо-ванных
объектов от числа максимально возможных. Характеризует уровень развития
добровольного страхования
|
|
Страховой платеж на 1 руб.
страховой суммы
|
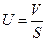
|
Характеризует тарифную ставку
страхования
|
|
Частота страховых случаев
|
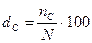
|
Показывает, сколько стра-ховых
случаев приходится в расчёте на 100 или 1000 застрахованных объектов. Можно
интерпретировать как вероятность гибели или повреждения застрахован-ного
имущества. Всегда <
1.
|
|
Уровень опустошительности
страхового случая (коэф-фициент кумуляции риска)
|
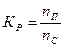
|
Показывает, сколько объектов
пострадало в одном страховом случае
|
|
Доля пострадавших объек-тов из
числа застрахованных
|
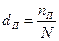
|
|
|
Коэффициент выплат страхового
возмещения (норма убыточности)
|
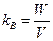
|
Показывает,
сколько копеек выплачивается в качестве страхового возмещения с каждого рубля
страхового платежа. Если величина этого показателя >1, то стра-хование имущества убы-точно. В динамике этот показатель
должен уменьшаться.
|
|
Полнота уничтожения пострадавших
объектов (коэффициент ущербности)
|
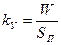
|
Характеризует удельный вес
суммы возмещения в страховой сумме постра-давших объектов. Если показатель
равен 1, значит, в результате
страхового слу-чая ущерб равен
дейст-вительной стоимости застра-хованного имущества. Та-кой ущерб называется
пол-ным ущербом. Если 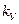 <1, ущерб называется частичным. <1, ущерб называется частичным.
|
|
Уровень убыточности страховых сумм
|
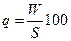
|
Показывает, сколько рублей
возмещается на каждый рубль страховой суммы
|
Уровень убыточности
страховых сумм – важнейший показатель имущественного страхования. Он зависит
от:
·
количества
заключённых договоров, N,
·
страховой
суммы застрахованных объектов, S,
·
числа
пострадавших объектов, nП
·
полноты
уничтожения застрахованных объектов, 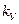 ,
,
·
суммы
выплат страхового возмещения, W.
Таким образом, он
является результатом взаимодействия пяти из семи основных объемных показателей.
Уровень убыточности
используется при обосновании ставок страховых платежей. Таким образом, этот
показатель влияет на показатель «сумма поступивших страховых платежей».
Одной из задач
статистики имущественного страхования является определение уровня тарифных ставок.
Тарифная ставка
определяет, сколько денег каждый из страхователей должен внести в общий
страховой фонд с единицы страховой суммы. Поэтому тарифы должны быть рассчитаны
так, чтобы сумма собранных взносов оказалась достаточной для выплат,
предусмотренных условиями страхования. Таким образом, тарифная ставка – это
цена услуги, оказываемой страховщиком населению, т.е. своеобразная цена
страховой защиты.
Полная тарифная
ставка называется брутто-ставкой. В основе определения размеров страховых
платежей лежит уровень тарифной ставки. Различают нетто-ставку 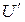 и брутто-ставку
и брутто-ставку 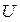 .
.
Нетто-ставка (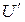 ) выражает рисковую часть тарифа для обеспечения страхового
возмещения и предназначена для формирования страхового фонда.
) выражает рисковую часть тарифа для обеспечения страхового
возмещения и предназначена для формирования страхового фонда.
Брутто-ставка (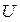 ) состоит из нетто-ставки и нагрузки к ней.
) состоит из нетто-ставки и нагрузки к ней.
Нагрузка (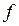 ) служит для покрытия накладных расходов страхования и образования
резервных фондов.
) служит для покрытия накладных расходов страхования и образования
резервных фондов.
Сравнение этого показателя позволяет
сделать выводы об изменении во времени (или пространстве) уровня устойчивости
страхового дела. Чем меньше этот коэффициент, тем устойчивее финансовое состояние.
Нетто-ставка вычисляется с
определённой степенью вероятности по формуле:
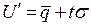 ,
,
где 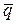 - средний уровень убыточности за период;
- средний уровень убыточности за период;
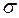 - среднее квадратическое отклонение индивидуальных уровней
убыточности от среднего уровня:
- среднее квадратическое отклонение индивидуальных уровней
убыточности от среднего уровня:
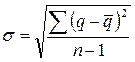 ,
,
где t – коэффициент доверительной вероятности, определяемой по таблице
на основании заданной вероятности.
Брутто-ставка рассчитывается по формуле:
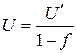 ,
,
где 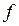 - доля нагрузки по
страхованию имущества в брутто-ставке.
- доля нагрузки по
страхованию имущества в брутто-ставке.
1.3. Показатели статистики личного страхования.
Личное страхование выступает формой социальной защиты и укрепления материального
благосостояния населения. Его объекты – жизнь, здоровье, трудоспособность
граждан. Договор личного страхования может быть обязательным (в силу закона)
или добровольным; долгосрочным (свыше 1 года и до 15 лет), краткосрочным (менее
1 года) и страхование жизни на всю жизнь.
Личное страхование состоит из двух
подотраслей: страхование жизни и страхование от несчастных случаев. Наиболее
распространенным считается смешанное страхование жизни с широким объемом
страховой ответственности (в связи с дожитием до окончания срока страхования, в
связи с потерей здоровья от несчастного случая, в связи с наступлением смерти
застрахованного), страхование детей и школьников от несчастных случае,
ритуальное страхование, страхование пенсий, страхование образования. Эти виды
объединяются в группу страхование жизни.
Договор личного страхования –
гражданско-правовая сделка, по которой страховщик обязуется посредством
получения им страховых взносов, в случае наступления страхового случая,
возместить в указанный срок нанесенный ущерб или произвести выплату страхового
капитала, ренты или других предусмотренных
выплат.
Страховые суммы определяются в
соответствии с компенсациями страхователя исходя из его материальных
возможностей.
Показатели личного страхования
отличны от показателей имущественного страхования, т.к. жизнь или смерть не
может быть объективно оценена. Застрахованный может лишь попытаться
предотвратить те материальные трудности, с которыми сталкивается в случае
смерти или инвалидности.
Застрахованный – объект,
подвергающийся риску, связанному с его жизнью, физической полноценностью или
здоровьем.
Страховые суммы не представляю
собой стоимость нанесенных материальных убытков или ущерба, которые не могут
быть объективно выражены, а определяются в соответствии с пожеланиями
страхователя исходя из его материальных возможностей. В отличие от
имущественного страхования некоторые виды личного страхования, в частности
жизни, рассчитаны на всю жизнь.
Тарифные ставки в страховании жизни
состоят из нескольких частей. Возьмём для примера смешанное страхование жизни,
в котором объединяются несколько видов страхования: 1) страхование на дожитие;
2) страхование на случай смерти; 3) страхование от несчастных случаев. По
каждому из них создается страховой фонд, поэтому тарифная ставка в смешанном страховании
состоит из трёх частей, входящих в нетто-ставку, и четвёртой части – нагрузки.
Так как рассмотренные страховые
события являются массовыми, имеют вероятностный характер и связываются с
возрастом застрахованных, то при установлении тарифных ставок используется
теория вероятностей и таблицы смертности и средней продолжительности
предстоящей жизни, которые строятся на основе переписей населения и наблюдений
страхового учреждения.
1.4. Основные показатели
деятельности страховых
организаций.
По данным ФССН за 9
месяцев 2007 года объем премии на страховом рынке увеличился на 24,9% и
составил 563,5 млрд. руб. Основная доля премий пришлась на добровольные виды
страхования — 306,4 млрд. руб. (рост на 19,7%). При этом выплаты выросли на
37,6% до 332,6 млрд. руб.
Таблица 1.
Страховые премии, млрд. руб.
|
Виды страхования
|
9 м. 2007
|
Прирост
|
9 м. 2006
|
|
Страховая премия (всего)
|
563,5
|
24,9%
|
451,2
|
|
Добровольное страхование
|
306,4
|
19,7%
|
255,9
|
|
страхование жизни
|
17,6
|
50,4%
|
11,7
|
|
иное, чем жизнь
|
288,8
|
18,2%
|
244,3
|
|
личное страхование
|
72,3
|
14,5%
|
63,1
|
|
имущества
|
201,1
|
19,3%
|
168,5
|
|
ответственности
|
15,4
|
22,2%
|
12,6
|
|
Обязательное страхование, в т.ч.
|
257,1
|
31,7%
|
195,2
|
|
ОСАГО
|
52,8
|
15,3%
|
45,8
|
|
ОМС
|
198,2
|
38,0%
|
143,7
|
|
Таблица 2.
Страховые выплаты, млрд. руб.
|
Виды страхования
|
9 м. 2007
|
Прирост
|
9 м. 2006
|
|
Страховые выплаты (всего)
|
332,6
|
37,6%
|
241,8
|
|
Добровольное страхование
|
110,8
|
33,3%
|
83,1
|
|
страхование жизни
|
11,8
|
11,8%
|
10,6
|
|
иное, чем жизнь
|
98,9
|
36,5%
|
72,5
|
|
личное страхование
|
35,1
|
17,7%
|
29,8
|
|
имущества
|
62,7
|
50,5%
|
41,6
|
|
ответственности
|
1,1
|
12,9%
|
1,0
|
|
Обязательное страхование, в т.ч.
|
221,8
|
39,8%
|
158,7
|
|
ОСАГО
|
29,1
|
23,9%
|
23,5
|
|
ОМС
|
189,4
|
43,4%
|
132,0
|
|
Точкой роста отечественного
страхового рынка в 2007 году стало страхование имущества, на которое пришлось
36% всех сборов. Компаниям, активно работающим в этом сегменте, удалось
увеличить объем премий на 30-50% (в первую очередь, за счет страхования
автокаско). Однако, несмотря на хорошие показатели отдельных страховщиков,
рентабельность рынка в целом снижается, - выплаты растут быстрее сборов.
Ситуация с убыточностью в ОСАГО
близка к критической и в ближайший год будет только ухудшаться. Продолжающийся
в течение последнего времени бурный рост продаж автомобилей в кредит, рост
автопарка физических и юридических лиц в стоимостном и количественном выражении
будет наблюдаться и в 2008 году. Скорее всего, по итогам 2007 года, мы еще
станем свидетелями роста продаж новых иномарок на 60%-70%, но в дальнейшем
динамика продаж должна снизиться. В перспективе ожидается снижение динамики
премии по автокаско более чем на 10 процентных пунктов.
Рост рынка страхования жизни не
связан с увеличением спроса на долгосрочные накопительные продукты, а отражает
предусмотренный законом процесс передачи портфелей в специализированные
компании. Вступающие в силу поправки в НК, посвященные изменениям в
налогообложении операций по страхованию жизни, не сильно повлияют на рынок
долгосрочного индивидуального страхования жизни и страхования жизни за счет
юридических лиц.
Развитие корпоративного добровольного
медицинского страхования дает импульс сегменту индивидуального страхования, как
в ДМС, так и в страховании от несчастных случаев: расширяется линейка
продуктов, разрабатываемых специально для физических лиц. Но пока значительная
часть объема страховой премии по индивидуальному ДМС приходится на
ограниченные, узкоспециализированные программы.
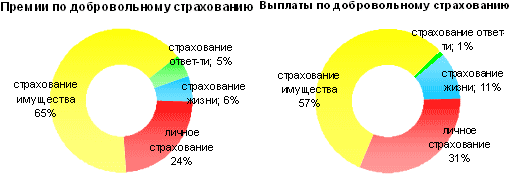
Перераспределение долей
в структуре премий различных видов добровольного страхования оказалось в
исследуемом периоде незначительным. В основном оно обусловлено ростом доли
страхования жизни (с 4,6% за 9 мес. 2006 г. до 5,7% в 2007 г.). В структуре выплат
по добровольному страхованию существенно увеличилась доля страхования
имущества: с 50% до 57%, прежде всего, за счет роста убыточности по
автострахованию. Доля страховых выплат по личному страхованию снизилась с 36%
до 31% (что произошло из-за высокого опережающего роста выплат в имущественном
страховании — более 50%), однако уровень выплат в данном сегменте продолжает
расти (48,6% за 9 мес. 2007 г.
против 47,3% за 9 месяцев 2006
г.).
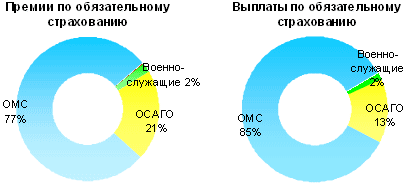
В структуре премии по обязательным
видам страхования несколько уменьшилась по сравнению с 9 месяцами 2006 г. доля ОСАГО: с 23,4%
до 20,5%. Соответственно доля взносов по ОМС увеличилась: с 73,6% до 77,1%. Произошло
это за счет опережающего по сравнению с ОСАГО темпа роста объема взносов по ОМС
(43,4% против 23,9%). В структуре выплат по обязательному страхованию существенных
изменений не произошло
2. РАСЧЕТНАЯ ЧАСТЬ
Имеются следующие выборочные данные о деятельности страховых
организаций одного из регионов в отчетном году (выборка 10%-ная, механическая)
Таблица 1.
Исходные данные
|
№ организации
|
Доходы, млн. руб.
|
Прибыль, млн. руб.
|
№ организации
|
Доходы, млн. руб.
|
Прибыль, млн. руб.
|
|
1
|
9,7
|
0,41
|
16
|
8
|
0,4
|
|
2
|
9
|
0,4
|
17
|
12,2
|
0,58
|
|
3
|
10,2
|
0,45
|
18
|
13,5
|
0,63
|
|
4
|
10,3
|
0,46
|
19
|
13,9
|
0,65
|
|
5
|
9,8
|
0,42
|
20
|
10,5
|
0,49
|
|
6
|
10
|
0,44
|
21
|
10,7
|
0,5
|
|
7
|
6
|
0,25
|
22
|
10,8
|
0,5
|
|
8
|
10,5
|
0,48
|
23
|
8,5
|
0,34
|
|
9
|
160
|
0,75
|
24
|
8,5
|
0,35
|
|
10
|
11,6
|
0,53
|
25
|
12,2
|
0,58
|
|
11
|
11,7
|
0,54
|
26
|
11,5
|
0,52
|
|
12
|
12,8
|
0,56
|
27
|
13,3
|
0,6
|
|
13
|
11,9
|
0,55
|
28
|
13,3
|
0,64
|
|
14
|
8,5
|
0,38
|
29
|
15
|
0,7
|
|
15
|
7
|
0,31
|
30
|
13,5
|
0,64
|
2.1. Выполнение задания 1.
Целью выполнения
данного Задания
является изучение состава и структуры выборочной совокупности страховых
организаций путем построения и анализа статистического ряда распределения
страховых организаций по признаку Доходы.
2.1.1. Построение интервального ряда распределения страховых
организаций по доходам.
Для построения
интервального вариационного ряда, характеризующего распределение страховых
организаций по доходам, необходимо вычислить величину и границы
интервалов ряда.
При построении ряда с
равными интервалами величина интервала h определяется по формуле
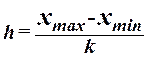 , (1)
, (1)
где 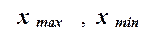 – наибольшее и наименьшее значения
признака в исследуемой совокупности, k- число групп интервального ряда.
– наибольшее и наименьшее значения
признака в исследуемой совокупности, k- число групп интервального ряда.
Число групп k задается в условии задания , n - число единиц
совокупности.
Определение величины интервала по
формуле (1) при заданных k
= 5, xmax = 16 млн руб., xmin = 6 млн
руб.:
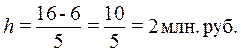
При
h = 2 млн
руб. границы интервалов ряда распределения имеют следующий вид (табл. 2):
Таблица 2.
|
Номер группы
|
Нижняя граница, млн. руб.
|
Верхняя граница, млн. руб.
|
|
1
|
6
|
8
|
|
2
|
8
|
10
|
|
3
|
10
|
12
|
|
4
|
12
|
14
|
|
5
|
14
|
16
|
Процесс группировки единиц
совокупности по признаку Доходы представлен во вспомогательной
(разработочной) таблице 3.
Таблица 3.
Разработочная
таблица для построения интервального
ряда распределения и
аналитической группировки.
|
Группы страховых организаций по доходам,
млн. руб.
|
Номер страховой организации
|
Сумма доходов, млн. руб.
|
Сумма прибыли, млн. руб.
|
|
1
|
2
|
3
|
4
|
|
6,00-8,00
|
7
|
6,00
|
0,25
|
|
|
15
|
7,00
|
0,31
|
|
Всего
|
2
|
13,00
|
0,56
|
|
8,00-10,00
|
1
|
9,70
|
0,41
|
|
|
2
|
9,00
|
0,40
|
|
|
5
|
9,80
|
0,42
|
|
|
14
|
8,50
|
0,38
|
|
|
16
|
8,00
|
0,40
|
|
|
23
|
8,50
|
0,34
|
|
|
24
|
8,50
|
0,35
|
|
Всего
|
7
|
62,00
|
2,70
|
|
10,00-12,00
|
3
|
10,20
|
0,45
|
|
|
4
|
10,30
|
0,46
|
|
|
6
|
10,00
|
0,44
|
|
|
8
|
10,50
|
0,48
|
|
|
10
|
11,60
|
0,53
|
|
|
11
|
11,70
|
0,54
|
|
|
13
|
11,90
|
0,55
|
|
|
20
|
10,50
|
0,49
|
|
|
21
|
10,70
|
0,50
|
|
|
22
|
10,80
|
0,50
|
|
|
26
|
11,50
|
0,52
|
|
Всего
|
11
|
119,70
|
5,46
|
|
12,0-14,00
|
12
|
12,80
|
0,56
|
|
|
17
|
12,20
|
0,58
|
|
|
18
|
13,50
|
0,63
|
|
|
19
|
13,90
|
0,65
|
|
|
25
|
12,20
|
0,58
|
|
|
27
|
13,30
|
0,60
|
|
|
28
|
13,30
|
0,64
|
|
|
30
|
13,50
|
0,64
|
|
Всего
|
8
|
104,70
|
4,88
|
|
14,00-16,00
|
9
|
16,00
|
0,75
|
|
|
29
|
15,00
|
0,70
|
|
Всего
|
2
|
31,00
|
1,45
|
|
ИТОГО
|
30
|
330,40
|
15,05
|
На основе
групповых итоговых строк «Всего» табл. 3 формируется итоговая таблица 4,
представляющая интервальный ряд распределения страховых организаций по доходам
Таблица 4.
Распределение страховых организаций по доходам
|
Номер группы
|
Группы страховых организаций по
доходам, млн. руб.
Х
|
Число организаций f
|
|
1
|
6,00-8,00
|
2
|
|
2
|
8,00-10,00
|
7
|
|
3
|
10,00-12,00
|
11
|
|
4
|
12,00-14,00
|
8
|
|
5
|
14,00-16,00
|
2
|
|
|
Итого
|
30
|
Помимо частот
групп в абсолютном выражении в анализе интервальных рядов используются ещё три
характеристики ряда: частоты групп в
относительном выражении, накопленные
(кумулятивные) частоты Sj, получаемые путем последовательного
суммирования частот всех предшествующих (i-1) интервалов, и накопленные
частости, рассчитываемые по формуле
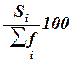 (2)
(2)
Таблица 5.
Структура страховых организаций по доходам.
|
№ группы
|
Группы страховых организаций по доходам,
млн. руб.
|
Группы страховых организаций по
доходам, fi
|
Накопленная частота, Si
|
Накопленная частость, %
|
|
В абсолютном выражении
|
в % к итогу
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
6,00-8,00
|
2
|
6,67
|
2
|
6,67
|
|
2
|
8,00-10,00
|
7
|
23,33
|
9
|
30,00
|
|
3
|
10,00-12,00
|
11
|
36,67
|
20
|
66,67
|
|
4
|
12,00-14,00
|
8
|
26,67
|
28
|
93,34
|
|
5
|
14,00-16,00
|
2
|
6,67
|
30
|
100,00
|
|
|
Итого
|
30
|
100,00
|
|
|
Вывод: анализ интервального ряда
распределения изучаемой совокупности страховых организаций показывает что:
1.
Преобладают страховые организации с величиной доходов от 10 до 12 млн. руб. (11
организаций, доля которых составляет 36,67%)
2. 9
страховых организаций имеют доход до 10 млн. руб., а 93,34% страховых организаций
– до 14 млн. руб.
2.1.2. Нахождение
средних характеристик, моды и медианы полученного интервального ряда
распределения путем расчетов и графическим методом.
Для расчета характеристик
ряда распределения 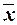 , σ, σ2, Vσ на основе табл. 5 строится
вспомогательная таблица 6 (xi – середина i-го интервала).
, σ, σ2, Vσ на основе табл. 5 строится
вспомогательная таблица 6 (xi – середина i-го интервала).
Таблица 6.
Расчетная таблица для нахождения характеристик ряда
распределения
|
Группы страховых организаций по
доходам, млн. руб.
|
Средняя интервала x'i
|
Число страховых организаций, ƒi
|
 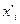 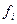
|
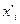 - -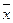
|
(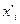 - -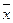 ) )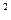
|
(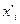 - -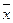 ) )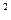 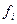
|
|
6,00-8,00
|
7,00
|
2
|
14
|
-4,067
|
16,538
|
33,076
|
|
8,00-10,00
|
9,00
|
7
|
63
|
-2,067
|
4,271
|
29,898
|
|
10,00-12,00
|
11,00
|
11
|
121
|
-0,067
|
0,004
|
0,049
|
|
12,00-14,00
|
13,00
|
8
|
104
|
1,933
|
3,738
|
29,902
|
|
14,00-16,00
|
15,00
|
2
|
30
|
3,933
|
15,471
|
30,942
|
|
Итого
|
|
30
|
332
|
|
|
123,867
|
Расчет
средней арифметической взвешенной:
(3) 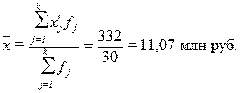
Расчет дисперсии:
(4)


Расчет
среднеквадратического отклонения:
(5) 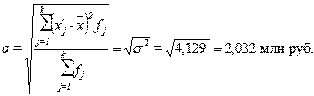
Расчет коэффициента
вариации:
(6) 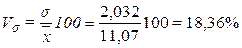
В интервальном
вариационном ряду модой приближенно считается центральное значение модального
интервала (имеющего наибольшую частоту). Более точно моду можно
определить графическим методом по гистограмме ряда (рис.1).
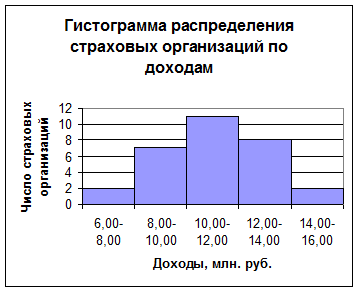
Рис.1
Гистограмма распределения страховых организаций по доходам.
Конкретное значение моды
для интервального ряда рассчитывается по формуле:
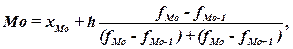 (7)
(7)
где
хМo – нижняя граница модального
интервала,
h –величина модального интервала,
fMo – частота модального интервала,
fMo-1 – частота интервала, предшествующего модальному,
fMo+1 –
частота интервала, следующего за модальным
Согласно табл. 4
модальным интервалом построенного ряда является интервал 10,00 – 12,00 млн.
руб., так как его частота максимальна (f3 = 11).
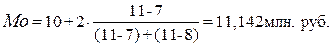
Вывод. Для рассматриваемой совокупности
страховых организаций наиболее распространенный доход характеризуется средней
величиной 11,142 млн. руб.
Медиану можно определить
графическим методом по кумулятивной кривой (рис. 2). Кумулята строится по
накопленным частотам (табл. 5, графа 5)
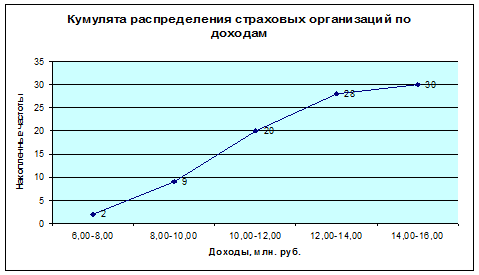
Рис. 2 Кумулята распределения страховых организаций по доходам.
Конкретное значение
медианы для интервального ряда рассчитывается по формуле:
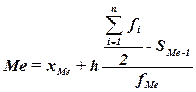 ,
(8)
,
(8)
где
хМе– нижняя
граница медианного интервала,
h – величина медианного интервала,
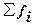 – сумма всех частот,
– сумма всех частот,
fМе – частота медианного интервала,
SMе-1 – кумулятивная (накопленная) частота
интервала, предшествующего медианному.
Расчет значения медианы по формуле:
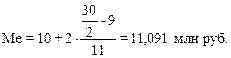
Вывод. В рассматриваемой совокупности
страховых организаций полови-
на страховых организаций имеют в
среднем доходы не более 11,091 млн. руб., а
другая половина – не менее 11,091
млн. руб.
Вывод: Анализ полученных значений
показателей 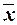 и σ говорит о том, что
средний доход страховых организаций составляет 11,07 млн руб., отклонение от
среднего дохода в ту или иную сторону составляет в среднем 2,032 млн руб. (или
18,36%), наиболее характерные значения дохода
находятся в пределах от 9,035 млн руб. до 13,099 млн руб. (диапазон
и σ говорит о том, что
средний доход страховых организаций составляет 11,07 млн руб., отклонение от
среднего дохода в ту или иную сторону составляет в среднем 2,032 млн руб. (или
18,36%), наиболее характерные значения дохода
находятся в пределах от 9,035 млн руб. до 13,099 млн руб. (диапазон 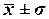 ).
).
Значение Vσ = 18,36% не превышает 33%,
следовательно, вариация доходов в исследуемой совокупности страховых
организаций незначительна и совокупность по данному признаку качественно
однородна. Расхождение между значениями 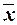 , Мо и Ме незначительно (
, Мо и Ме незначительно (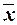 =11,07 млн. руб., Мо=11,142
млн. руб., Ме=11,091 млн. руб.), что
подтверждает вывод об однородности совокупности страховых организаций. Таким
образом, найденное среднее значение объема доходов страховых организаций (11,07
млн. руб.) является типичной, надежной характеристикой исследуемой совокупности
страховых организаций.
=11,07 млн. руб., Мо=11,142
млн. руб., Ме=11,091 млн. руб.), что
подтверждает вывод об однородности совокупности страховых организаций. Таким
образом, найденное среднее значение объема доходов страховых организаций (11,07
млн. руб.) является типичной, надежной характеристикой исследуемой совокупности
страховых организаций.
2.2. Выполнение задания 2.
Целью выполнения
данного Задания
является выявление наличия корреляционной связи между факторным и
результативным признаками, установление направления связи и оценка ее тесноты.
По условию Задания 2 факторным является признак Доходы (X), результативным
– признак Прибыль (Y).
2.2.1. Установление наличия и
характера связи между признаками Доходы и Прибыль методом аналитической
группировки.
При использовании метода аналитической группировки строится
интервальный ряд распределения единиц совокупности по факторному признаку Х и для каждой i-ой группы ряда определяется среднегрупповое значение 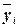 результативного признака Y. Если с ростом значений фактора Х от группы к группе средние значения
результативного признака Y. Если с ростом значений фактора Х от группы к группе средние значения 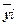 систематически
возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.
систематически
возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.
Таблица 7.
Аналитическая
группировка зависимости доходов и прибыли страховых
организаций.
|
№ группы
|
Группы страховых организаций по
доходам, млн. руб.
|
Число страховых организаций, ¦i
|
Доходы страховых организаций, млн. руб.
|
Прибыль страховых организаций, млн.
руб.
|
|
Всего
|
В среднем по группе на 1 страховую
организацию,
|
Всего
|
В среднем по группе на 1 страховую организацию,
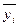
|
|
1
|
6,00-8,00
|
2
|
13,00
|
6,50
|
0,56
|
0,28
|
|
2
|
8,00-10,00
|
7
|
62,00
|
8,86
|
2,70
|
0,39
|
|
3
|
10,00-12,00
|
11
|
119,70
|
10,88
|
5,46
|
0,50
|
|
4
|
12,00-14,00
|
8
|
104,70
|
13,09
|
4,88
|
0,61
|
|
5
|
14,00-16,00
|
2
|
31,00
|
15,50
|
1,45
|
0,73
|
|
Итого
|
|
30
|
330,40
|
11,01
|
15,05
|
0,50
|
Вывод. Анализ
данных табл. 7 показывает, что с увеличением дохода от группы к группе систематически возрастает
и средняя прибыль по каждой группе страховых организаций, что свидетельствует о
наличии прямой корреляционной связи между исследуемыми признаками.
2.2.2. Измерение
тесноты корреляционной связи между признаками Доходы и Прибыль с использованием
коэффициентов детерминации и эмпирического корреляционного отношения
Для построения корреляционной
таблицы необходимо знать величины и границы интервалов по двум признакам X и Y. Величина интервала и границы интервалов для
факторного признака Х
– Доходы известны из табл. 7. Для
результативного признака Y – Прибыль величина интервала определяется
по формуле (1) при k
= 5, уmax = 0,75 млн руб., уmin =0,25 млн
руб.:
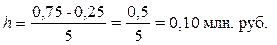
Границы
интервалов ряда распределения результативного признака Y имеют следующий вид (табл.
8):
Таблица 8.
|
.№ группы
|
Нижняя граница, млн. руб.
|
Верхняя граница, млн. руб.
|
|
1
|
0,25
|
0,35
|
|
2
|
0,35
|
0,45
|
|
3
|
0,45
|
0,55
|
|
4
|
0,55
|
0,65
|
|
5
|
0,65
|
0,75
|
Подсчитывая с использованием принципа полуоткрытого
интервала [ ) число
страховых организаций, входящих в каждую группу (частоты групп), получаем интервальный
ряд распределения результативного признака (табл. 9).
Таблица
9.
Распределение
страховых
организаций
по прибыли
|
Группы страховых организаций по
прибыли, x
|
Число страховых организаций, ¦i
|
|
0,25-0,35
|
3
|
|
0,35-0,45
|
7
|
|
0,45-0,55
|
9
|
|
0,55-0,65
|
8
|
|
0,65-0,75
|
3
|
|
Итого
|
30
|
Используя группировки по факторному и результативному
признакам, строим корреляционную таблицу (табл. 10)
Таблица
10.
Корреляционная таблица зависимости прибыли страховых организаций
от их дохода.
|
Группы страховых организаций по
доходам, млн. руб.
|
Группы страховых организаций по сумме
прибыли, млн. руб.
|
Итого
|
|
0,25-0,35
|
0,35-0,45
|
0,45-0,55
|
0,55-0,65
|
0,65-0,75
|
|
6,00-8,00
|
2
|
0
|
0
|
0
|
0
|
2
|
|
8,00-10,00
|
1
|
6
|
0
|
0
|
0
|
7
|
|
10,00-12,00
|
0
|
1
|
9
|
1
|
0
|
11
|
|
12,00-14,00
|
0
|
0
|
0
|
7
|
1
|
8
|
|
14,00-16,00
|
0
|
0
|
0
|
0
|
2
|
2
|
|
Итого
|
3
|
7
|
9
|
8
|
3
|
30
|
Вывод. Анализ данных табл. 10 показывает,
что распределение частот групп произошло вдоль диагонали, идущей из левого
верхнего угла в правый нижний угол таблицы. Это свидетельствует о наличии
прямой корреляционной связи между доходами и прибылью страховых организаций.
Для измерения тесноты
связи между факторным и результативным признаками рассчитаем специальные
показатели – эмпирический коэффициент детерминации 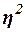 и эмпирическое
корреляционное отношение
и эмпирическое
корреляционное отношение 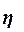 .
.
Эмпирический коэффициент детерминации 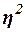 рассчитывается как
доля межгрупповой дисперсии в общей дисперсии по формуле
рассчитывается как
доля межгрупповой дисперсии в общей дисперсии по формуле
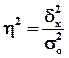 ,
(9)
,
(9)
где 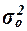 – общая дисперсия
признака Y,
– общая дисперсия
признака Y,
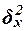 – межгрупповая
(факторная) дисперсия признака Y.
– межгрупповая
(факторная) дисперсия признака Y.
Значения показателя 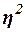 изменяются в пределах
изменяются в пределах
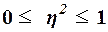 . При отсутствии корреляционной связи
между признаками Х и Y имеет место равенство
. При отсутствии корреляционной связи
между признаками Х и Y имеет место равенство 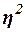 =0, а при наличии функциональной связи
между ними - равенство
=0, а при наличии функциональной связи
между ними - равенство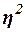 =1.
=1.
Общая дисперсия
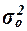 характеризует
вариацию результативного признака, сложившуюся под влиянием всех действующих на
Y факторов (систематических
и случайных). Этот показатель вычисляется по формуле
характеризует
вариацию результативного признака, сложившуюся под влиянием всех действующих на
Y факторов (систематических
и случайных). Этот показатель вычисляется по формуле
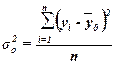 ,
(10)
,
(10)
где yi – индивидуальные значения
результативного признака;
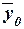 – общая средняя значений результативного
признака;
– общая средняя значений результативного
признака;
n – число единиц совокупности.
Общая
средняя 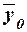 вычисляется как средняя арифметическая простая
по всем единицам совокупности:
вычисляется как средняя арифметическая простая
по всем единицам совокупности:
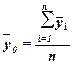 (11)
(11)
или
как средняя взвешенная по частоте групп интервального ряда:
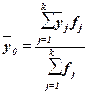 (12)
(12)
Для
вычисления 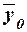 удобно использовать
формулу (11), т.к. в табл. 7 (графы 3 и 6 итоговой строки) имеются значения
числителя и знаменателя формулы.
удобно использовать
формулу (11), т.к. в табл. 7 (графы 3 и 6 итоговой строки) имеются значения
числителя и знаменателя формулы.
Расчет
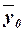 по формуле (11):
по формуле (11):
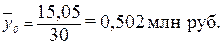
Для расчета общей
дисперсии 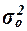 применяется вспомогательная таблица
11.
применяется вспомогательная таблица
11.
Таблица 11.
Вспомогательная таблица для расчета общей
дисперсии
|
№ страховой организации
|
Прибыль, млн. руб.
|
 - -
|
( - -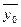 )² )²
|
 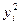
|
|
1
|
0,41
|
-0,092
|
0,008
|
0,168
|
|
2
|
0,40
|
-0,102
|
0,010
|
0,160
|
|
3
|
0,45
|
-0,052
|
0,003
|
0,203
|
|
4
|
0,46
|
-0,042
|
0,002
|
0,212
|
|
5
|
0,42
|
-0,082
|
0,007
|
0,176
|
|
6
|
0,44
|
-0,062
|
0,004
|
0,194
|
|
7
|
0,25
|
-0,252
|
0,064
|
0,063
|
|
8
|
0,48
|
-0,022
|
0,000
|
0,230
|
|
9
|
0,75
|
0,248
|
0,062
|
0,563
|
|
10
|
0,53
|
0,028
|
0,001
|
0,281
|
|
11
|
0,54
|
0,038
|
0,001
|
0,292
|
|
12
|
0,56
|
0,058
|
0,003
|
0,314
|
|
13
|
0,55
|
0,048
|
0,002
|
0,303
|
|
14
|
0,38
|
-0,122
|
0,015
|
0,144
|
|
15
|
0,31
|
-0,192
|
0,037
|
0,096
|
|
16
|
0,40
|
-0,102
|
0,010
|
0,160
|
|
17
|
0,58
|
0,078
|
0,006
|
0,336
|
|
18
|
0,63
|
0,128
|
0,016
|
0,397
|
|
19
|
0,65
|
0,148
|
0,022
|
0,423
|
|
20
|
0,49
|
-0,012
|
0,000
|
0,240
|
|
21
|
0,50
|
-0,002
|
0,000
|
0,250
|
|
22
|
0,50
|
-0,002
|
0,000
|
0,250
|
|
23
|
0,34
|
-0,162
|
0,026
|
0,116
|
|
24
|
0,35
|
-0,152
|
0,023
|
0,123
|
|
25
|
0,58
|
0,078
|
0,006
|
0,336
|
|
26
|
0,52
|
0,018
|
0,000
|
0,270
|
|
27
|
0,60
|
0,098
|
0,010
|
0,360
|
|
28
|
0,64
|
0,138
|
0,019
|
0,410
|
|
29
|
0,70
|
0,198
|
0,039
|
0,490
|
|
30
|
0,64
|
0,138
|
0,019
|
0,410
|
|
Итого
|
15,05
|
-0,01
|
0,417
|
7,967
|
Расчет общей
дисперсии по формуле
(10):
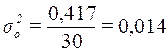
Общая дисперсия может
быть также рассчитана по формуле
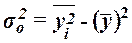 ,
,
где 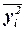 – средняя из квадратов значений
результативного признака,
– средняя из квадратов значений
результативного признака,
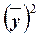 – квадрат средней величины значений
результативного признака.
– квадрат средней величины значений
результативного признака.
Для
демонстрационного примера
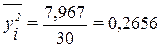
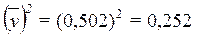
Тогда
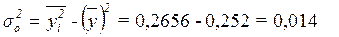
Межгрупповая
дисперсия 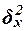 измеряет
систематическую вариацию результативного
признака, обусловленную влиянием признака-фактора Х (по которому произведена группировка). Воздействие фактора Х на результативный признак Y проявляется в отклонении групповых средних
измеряет
систематическую вариацию результативного
признака, обусловленную влиянием признака-фактора Х (по которому произведена группировка). Воздействие фактора Х на результативный признак Y проявляется в отклонении групповых средних 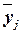 от
общей средней
от
общей средней 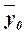 . Показатель
. Показатель 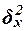 вычисляется по формуле
вычисляется по формуле
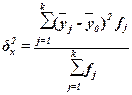 , (13)
, (13)
где 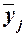 –групповые
средние,
–групповые
средние,
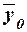 –
общая средняя,
–
общая средняя,
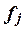 –число единиц в j-ой
группе,
–число единиц в j-ой
группе,
k – число групп.
Для расчета межгрупповой
дисперсии 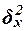 строится вспомогательная таблица 12. При этом
используются групповые средние значения
строится вспомогательная таблица 12. При этом
используются групповые средние значения 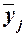 из табл. 7 (графа 7).
из табл. 7 (графа 7).
Таблица 12
Вспомогательная таблица для расчета межгрупповой
дисперсии.
|
Группы страховых организаций по доходам,
х
|
Число страховых организаций, ¦j
|
Прибыль страховых организаций всего,
млн. руб., у
|
Средняя прибыль страховых организаций
по группе, 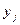
|
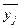 - -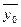
|
(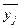 - -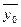 )² )²
|
(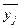 - -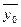 )²¦j )²¦j
|
|
6,00-8,00
|
2
|
0,560
|
0,280
|
-0,222
|
0,049
|
0,099
|
|
8,00-10,00
|
7
|
2,700
|
0,390
|
-0,112
|
0,013
|
0,088
|
|
10,00-12,00
|
11
|
5,460
|
0,500
|
-0,002
|
0,000
|
0,000
|
|
12,00-14,00
|
8
|
4,880
|
0,610
|
0,108
|
0,012
|
0,093
|
|
14,00-16,00
|
2
|
1,450
|
0,730
|
0,228
|
0,052
|
0,104
|
|
Итого
|
30
|
15,050
|
|
|
|
0,384
|
Расчет межгрупповой дисперсии 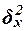 по формуле (11):
по формуле (11):
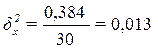
Расчет
эмпирического коэффициента детерминации 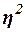 по формуле (9):
по формуле (9):
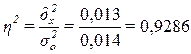 или 92,86%
или 92,86%
Вывод. 92,86% вариации суммы прибыли
страховых организаций обусловлено вариацией доходов, а 7,14% – влиянием прочих неучтенных факторов.
Эмпирическое корреляционное
отношение 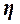 оценивает тесноту связи между факторным и
результативным признаками и вычисляется по формуле
оценивает тесноту связи между факторным и
результативным признаками и вычисляется по формуле
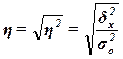 (14)
(14)
Значение показателя изменяются в пределах 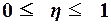 . Чем ближе значение
. Чем ближе значение 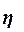 к 1, тем теснее связь между признаками. Для
качественной оценки тесноты связи на основе
к 1, тем теснее связь между признаками. Для
качественной оценки тесноты связи на основе 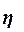 служит шкала Чэддока (табл. 13):
служит шкала Чэддока (табл. 13):
Таблица 13
Шкала Чэддока
|
h
|
0,1 –
0,3
|
0,3 – 0,5
|
0,5 – 0,7
|
0,7 – 0,9
|
0,9 – 0,99
|
|
Характеристика
силы
связи
|
Слабая
|
Умеренная
|
Заметная
|
Тесная
|
Весьма
тесная
|
Расчет эмпирического корреляционного
отношения 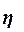 по формуле 14:
по формуле 14:
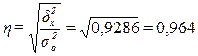 или 96,4%
или 96,4%
Вывод. Согласно шкале Чэддока связь между
доходами и суммой прибыли страховых
организаций является весьма тесной.
2.3. Выполнение Задания 3
Целью выполнения
данного Задания
является определение для генеральной совокупности страховых организаций границ,
в которых будут находиться величина доходов страховых организаций и доля страховых организаций с доходом 14
млн. руб. и более.
2.3.1. Определение
ошибки выборки для среднего дохода страховых организаций и границ, в которых
будет находиться генеральная средняя
Значения признаков
единиц, отобранных из генеральной совокупности в выборочную, всегда случайны,
поэтому и статистические характеристики выборки случайны, следовательно, и
ошибки выборки также случайны. Ввиду этого принято вычислять два вида ошибок -
среднюю 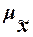 и предельную
и предельную 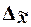 .
.
Для
собственно-случайной и механической выборки с бесповторным способом отбора
средняя ошибка 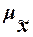 выборочной средней
выборочной средней 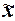 определяется по формуле
определяется по формуле
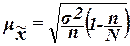 , (15)
, (15)
где 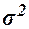 – общая дисперсия выборочных значений
признаков,
– общая дисперсия выборочных значений
признаков,
N – число единиц в генеральной
совокупности,
n – число единиц в выборочной
совокупности.
Предельная ошибка выборки 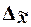 определяет границы, в пределах которых
будет находиться генеральная средняя:
определяет границы, в пределах которых
будет находиться генеральная средняя:
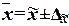 , (16)
, (16)
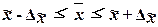 ,
,
где 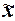 – выборочная средняя,
– выборочная средняя,
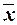 – генеральная средняя.
– генеральная средняя.
Границы задают доверительный
интервал генеральной средней, т.е. случайную область значений, которая
с вероятностью Р гарантированно содержит значение генеральной средней.
Предельная ошибка выборки
Δ кратна средней ошибке µ
с коэффициентом
кратности t (называемым также коэффициентом доверия), который зависит от значения доверительной
вероятности Р.
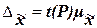 (17)
(17)
Для наиболее часто
используемых уровней надежности Р значения t задаются следующим образом (табл.
14):
Таблица 14
|
Доверительная вероятность P
|
0,683
|
0,866
|
0,954
|
0,988
|
0,997
|
0,999
|
|
Значение t
|
1,0
|
1,5
|
2,0
|
2,5
|
3,0
|
3,5
|
По условию
задания выборочная совокупность насчитывает 30 страховых организаций, выборка
10% механическая, следовательно, генеральная совокупность включает 300
страховых организаций. Выборочная средняя 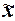 , дисперсия
, дисперсия 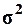 определены в Задании 1. Значения
параметров, необходимых для решения задачи, представлены в табл. 15:
определены в Задании 1. Значения
параметров, необходимых для решения задачи, представлены в табл. 15:
Таблица 15.
|
P
|
t
|
n
|
N
|
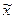
|
σ²
|
|
0,954
|
2
|
30
|
300
|
11,07
|
4,129
|
Рассчитаем
среднюю ошибку выборки:
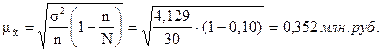
Рассчитаем предельную
ошибку выборки:
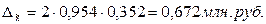
Определим доверительный интервал для
генеральной средней:


Вывод. На основании проведенного
выборочного обследования с вероятностью 0,954 можно утверждать, что для
генеральной совокупности страховых организаций средняя величина доходов
находится в пределах от 10,398 до 11,742 млн. руб.
2.3.2. Определение ошибки выборки для доли страховых организаций с
доходами 14 млн. руб. и более, а также
границ, в которых будет
находиться генеральная доля
Доля единиц выборочной
совокупности, обладающих тем или иным заданным свойством, выражается формулой
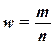 ,
,
где
m – число
единиц совокупности, обладающих заданным свойством;
n – общее число единиц в совокупности.
Для
собственно-случайной и механической выборки с бесповторным способом отбора предельная ошибка выборки 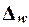 доли единиц,
обладающих заданным свойством, рассчитывается по формуле
доли единиц,
обладающих заданным свойством, рассчитывается по формуле
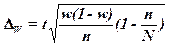 ,
,
где
w – доля
единиц совокупности, обладающих заданным свойством;
(1-w) – доля единиц совокупности, не обладающих заданным свойством,
N – число единиц в генеральной
совокупности,
n – число единиц в выборочной
совокупности.
Предельная
ошибка выборки 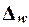 определяет границы, в пределах которых
будет находиться генеральная доля р единиц, обладающих исследуемым признаком:
определяет границы, в пределах которых
будет находиться генеральная доля р единиц, обладающих исследуемым признаком:
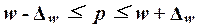
По условию Задания 3
исследуемым свойством фирм является равенство или превышение доходов страховых
организаций 14 млн. руб.
Число страховых
организаций с данным свойством определяется из табл. 3 (графа 3):
m=2
Рассчитаем выборочную
долю:

Рассчитаем предельную
ошибку выборки для доли:
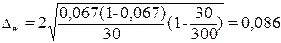
Определим доверительный
интервал генеральной доли:
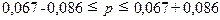
0,0
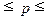 0,153
0,153
или
0%
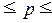 15,3%
15,3%
Вывод. С вероятностью 0,954 можно утверждать, что в
генеральной совокупности страховых организаций доля страховых организаций со средним доходом 14 млн. руб. и более будет находиться в пределах
от 0% до 15,3%.
2.4. Выполнение задания 4.
Определить тарифную ставку
страхования профессиональной ответственности аудиторов при средней убыточности
55 руб. на 100 руб. страховых сумм, экспертной оценке вероятности наступления
страхового события – 0,05, числе договоров – 1200, доле абсолютной нагрузки в
брутто-ставке – 25% и вероятности непревышения возмещения по сравнению со
страховыми суммами – 0,997

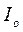 =
= 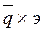 , где
, где
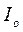 - основная часть нетто-ставки
- основная часть нетто-ставки
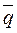 - средний уровень
убыточности страховых сумм
- средний уровень
убыточности страховых сумм
э –
экспертная оценка
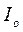 = 55
= 55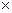 0,05 = 2,75 руб. на 100 руб.
0,05 = 2,75 руб. на 100 руб.
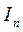 - рисковая надбавка
- рисковая надбавка
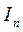 = 1,2
= 1,2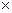
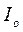
 t
t 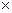
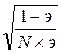 = 1,2
= 1,2 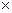 2,75
2,75 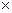 3
3 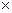
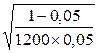 = 1,25 руб. со 100
руб.
= 1,25 руб. со 100
руб.
u – брутто-ставка
u = 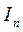 +
+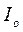 = 1,25 + 2,75 = 4 руб. со 100 руб. страховых сумм.
= 1,25 + 2,75 = 4 руб. со 100 руб. страховых сумм.
u’- нетто-ставка
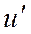 =
= 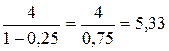 руб.
руб.
ЗАКЛЮЧЕНИЕ.
В
данной курсовой работе мы рассмотрели задачи статистики страхового
рынка. Статистика
занимается сбором, обработкой и анализом информации, происходящих в области
страхования; выявлением закономерностей появления страховых событий, оценкой их
частоты, тяжести и опустошительности; установлением тарифных ставок. В последнее
время страховой рынок России
характеризуется ростом числа страховых компаний и страховщиков, а также
объемов совершаемых ими операций, появлением новых потребностей и новых направлений их деятельности.
В расчетной части были выполнены задания по
теме и сделаны выводы по результатам их решений.
Построен
интервальный ряд распределения, анализ которого показал, что:
1.
Преобладают страховые организации с величиной доходов от 10 до 12 млн. руб. (11
организаций, доля которых составляет 36,67%)
2. 9
страховых организаций имеют доход до 10 млн. руб., а 93,34% страховых
организаций – до 14 млн. руб.
Найдены средние характеристики, мода
и медиана построенного ряда распределения, анализ которых показывает, что
средний доход страховых организаций составляет 11,07 млн руб., отклонение от
среднего дохода в ту или иную сторону составляет в среднем 2,032 млн руб. (или
18,36%), наиболее характерные значения дохода
находятся в пределах от 9,035 млн руб. до 13,099 млн руб. (диапазон 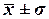 ).
).
Значение коэффициента
вариации (Vσ = 18,36%) не превышает 33%,
следовательно, вариация доходов в исследуемой совокупности страховых организаций
незначительна и совокупность по данному признаку качественно однородна.
Расхождение между значениями 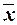 , Мо и Ме незначительно (
, Мо и Ме незначительно (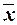 =11,07 млн. руб., Мо=11,142
млн. руб., Ме=11,091 млн. руб.), что
подтверждает вывод об однородности совокупности страховых организаций. Таким
образом, найденное среднее значение объема доходов страховых организаций (11,07
млн. руб.) является типичной, надежной характеристикой исследуемой совокупности
страховых организаций.
=11,07 млн. руб., Мо=11,142
млн. руб., Ме=11,091 млн. руб.), что
подтверждает вывод об однородности совокупности страховых организаций. Таким
образом, найденное среднее значение объема доходов страховых организаций (11,07
млн. руб.) является типичной, надежной характеристикой исследуемой совокупности
страховых организаций.
Установлено наличие и характер связи между
признаками Доходы и Прибыль методом аналитической группировки, анализ которых
показывает, что с увеличением дохода от
группы к группе систематически возрастает и средняя прибыль по каждой группе
страховых организаций, что свидетельствует о наличии прямой корреляционной
связи между исследуемыми признаками.
Измерена теснота корреляционной связи между признаками Доходы
и Прибыль с использованием коэффициентов детерминации и эмпирического
корреляционного отношения. Анализ полученных данных свидетельствует о наличии
прямой корреляционной связи между доходами и прибылью страховых организаций.
92,86% вариации суммы прибыли страховых организаций обусловлено вариацией
доходов, а 7,14% – влиянием прочих
неучтенных факторов. Связь между доходами и
суммой прибыли страховых организаций является весьма тесной.
Определена ошибка выборки для среднего дохода страховых
организаций и границы, в которых будет находиться генеральная средняя, исходя
из чего с вероятностью 0,954 можно
утверждать, что для генеральной совокупности страховых организаций средняя
величина доходов находится в пределах от 10,398 до 11,742 млн. руб.
Определена ошибка выборки для доли страховых организаций с
доходами 14 млн. руб. и более, а также
границы, в которых будет находиться генеральная доля. С вероятностью 0,954 можно утверждать, что в генеральной совокупности
страховых организаций доля страховых организаций со средним доходом 14 млн. руб. и более будет находиться в пределах
от 0% до 15,3%.
Список использованной
литературы.
1. Гусаров В.М., Статистика: учебное
пособие для вузов – М.: ЮНИТИ-ДАНА, 2001.
2. Гусаров В.М. Теория статистики:
Учебное пособие для вузов. – М.: Аудит, ЮНИТИ, 1998.
3. Практикум по статистике: Учебное
пособие для вузов / Под редакцией В.М. Симчеры / ВХФЭИ. – М.: ЗАО
«Финстатинформ», 1999.
4. «Статистика финансов» под редакцией
профессора В.Н. Салина. Москва. «Финансы и статистика», 2000.
5. http://www.insur-info.ru – сайт журнала «Страхование сегодня»
.