Задача
По
предприятиям легкой промышленности региона получена информация, характеризующая
зависимость объема выпуска продукции (Y, млн. руб.) от объема
капиталовложений (X, млн. руб.).
Требуется:
1. Найти параметры уравнения линейной
регрессии, дать экономическую интерпретацию коэффициента регрессии.
2. Вычислить остатки; найти остаточную
сумму квадратов; оценить дисперсию остатков S2ε ; построить график остатков.
3. Проверить выполнение предпосылок МНК.
4. Осуществить проверку значимости
параметров уравнения регрессии с помощью t-критерия Стьюдента (α=0,05).
5. Вычислить коэффициент детерминации,
проверить значимость уравнения регрессии с помощью f-критерия Фишера (α=0,05), найти
среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
6. Осуществить прогнозирование среднего
значения показателя Y при уровне значимости α=0,1, если прогнозное значение фактора X составит 80% от его максимального
значения.
7. Представить графически фактическое и
модельное значение Y точки прогноза.
8. Составить уравнения нелинейной
регрессии:
–
гиперболической;
–
степенной;
–
показательной.
Привести
графики построенных уравнений регрессии.
9. Для указанных моделей найти
коэффициенты детерминации, коэффициенты эластичности и средние относительные
ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.
|
Y
|
36
|
28
|
43
|
52
|
51
|
54
|
25
|
37
|
51
|
29
|
|
X
|
104
|
77
|
117
|
137
|
143
|
144
|
82
|
101
|
132
|
77
|
Решение.
Задача 1. Уравнение линейной регрессии имеет вид: 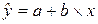 . А значения параметров а и b линейной модели можно определить по
данным формулам:
. А значения параметров а и b линейной модели можно определить по
данным формулам:
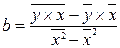 ,
, 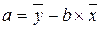 .
.
С
помощью ППП Excel найдем параметры уравнения линейной регрессии. Порядок выселения
следующий:
1. Активизируем
инструмент Пакет анализа:
1.1. Сервис →Настройки;
1.2. В диалоговом окне Настройки отметим пункт
Пакет анализа→ ОК.
2. Ведем исходные данные;
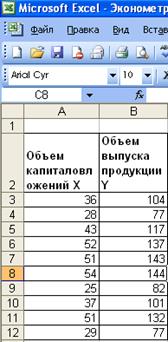
Рис. 1.
Исходные данные
3. Сервис → Анализ данных → Регрессия→ОК;
4. Заполним диалоговое окно ввода
данных и параметров вывода:
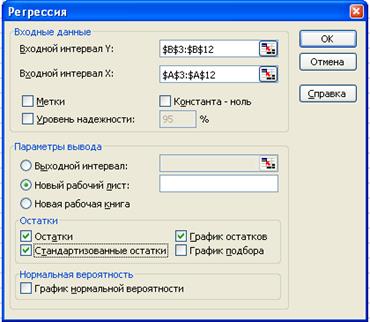
Рис. 2.
Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для
данных представлены на рис. 3.
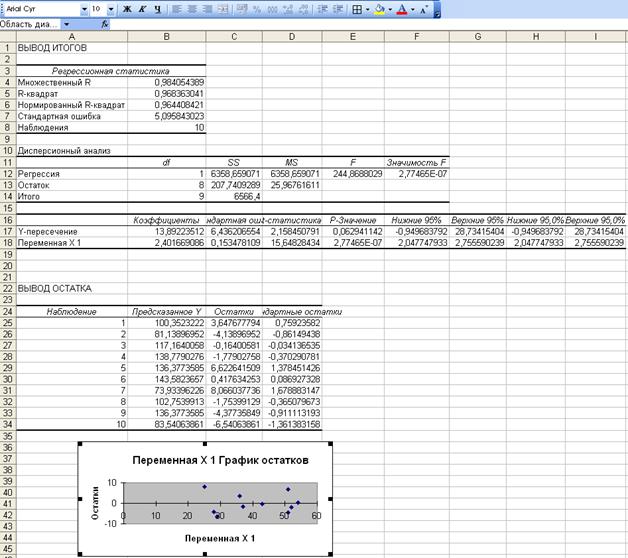
Рис. 3.
Результат применения инструмента Регрессия
В
ячейках В17 и В18 расположены значения параметров а и b соответственно. Итак, уравнение
регрессии имеет вид: 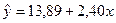 .
.
Коэффициент
регрессии b показывает, что с ростом капиталовложений на 1 млн. руб. выпуск
продукции увеличивается в среднем на 2,40 млн. руб.
Задача 2. Остатки определяются по формуле: 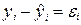 . Соответственно остаточная сумма квадратов определяется по
формуле:
. Соответственно остаточная сумма квадратов определяется по
формуле: 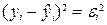 .
.
На
рис. 3. в ячейках С25:С34 уже вычислены остатки. А остаточную сумму квадратов
найдем с помощью ППП Excel, использую функцию ПРОИЗВЕД. Результаты вычислений
приведены на рис. 6.
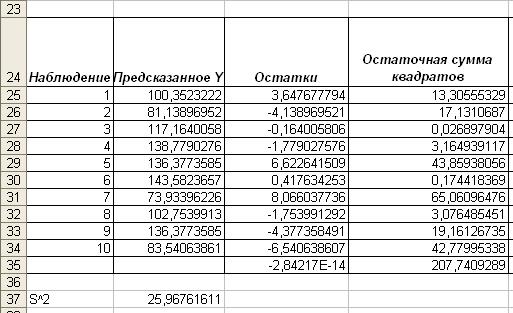
Рис. 4.
Остаточная сумма квадратов
Итак, остаточная сумма
квадратов равна 25,96– она также вычислена с помощью Регрессии (ячейка D13).
Дисперсия остатков
определяется по формуле: 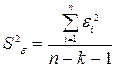 .
.
Поскольку
остаточная сумма квадратов вычислена и равна 25,96, а количество наблюдений 10,
то можно найти дисперсию остатков. Результат вычисления приведен на рис. 4 в
ячейке В37.
Итак, дисперсия остатков
составляет 25,96 (она также вычислена с помощью Регрессии – рис. 3, ячейка D13).
График остатков уже построен
с помощью инструмента Анализа данных Регрессия (рис. 3). Приведем график
остатков в отдельный вид.
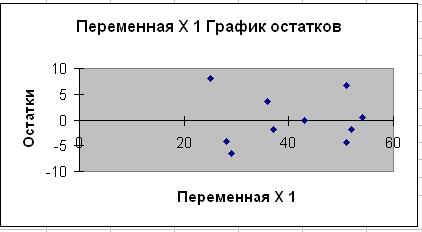
Рис. 5.
График остатков
Задача 3.
Проверим выполнение предпосылок МНК. Свойства коэффициентов регрессии
существенным образом зависят от свойств случайной составляющей. Для того чтобы МНК давал
наилучшие результаты, должны выполняться условия Гаусса- Маркова.
Условие 1. Математическое ожидание случайной
составляющей в любом наблюдении должно быть равно нулю: М(εi)=0.
В
нашем случае уравнение регрессии включает постоянный член и, следовательно, это
условие выполняется автоматически.
Условие 2. Случайная составляющая (εi) или зависимая переменная (yi)есть величины случайные, а
независимая величина (xi)– величина неслучайная: 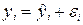 . Проверим выполнение данного условия с помощью критерия
поворотных точек, для этого постоим дополнительную таблицу.
. Проверим выполнение данного условия с помощью критерия
поворотных точек, для этого постоим дополнительную таблицу.
Таблица 1
|
Наблюдение
|
yi
|
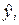
|
εi
|
P
|
|
1
2
3
4
5
6
7
8
9
10
|
104
77
117
137
143
144
82
101
132
77
|
100,35
81,14
117,16
138,78
136,38
143,58
73,93
102,75
136,38
83,54
|
3,64
-4,14
-0,16
-1,78
6,62
0,42
8,07
-1,75
-4,38
-6,54
|
-
1
1
1
1
1
1
0
0
-
|
|
Сумма
|
1114
|
1113,99
|
|
6
|
Р- число поворотных точек. В нашем
примере Р=6.
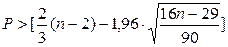 ;
;
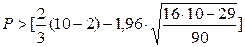 ;
;
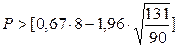 ;
;
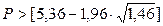 ;
;
Р> 2,99; т.е. 6>2,99. Следовательно, условие выполняется.
Итак,
случайная составляющая (εi) или зависимая переменная (yi) есть величины случайные.
Условие 3. Случайная переменная в любых двух
наблюдениях независима.
Чтобы
проверить выполнение данного условия, с помощью ППП Excel вычислим dw-критерий Дарбина - Уотсона: 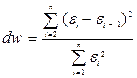 .
.
Т.к.
остатки и остаточная сумма квадратов уже вычислены (рис. 5),то для нахождения dw-критерий Дарбина – Уотсона
нужно найти (εi-εi-1) и (εi-εi-1)2.
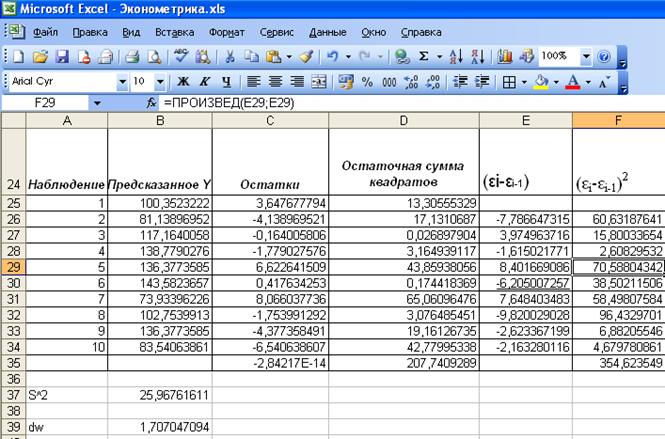
Рис. 6.
Вычисление dw-критерия Дарбина-Уотсона
Итак, dw=1,70. Поскольку dw > d2 (d2 = 1,36) , но dw < 2, т.е. в нашем случае
автокорреляции нет, следовательно, условие выполняется.
Условие 4. Дисперсия случайной составляющей
должна быть постоянной для всех наблюдений. Это условие гомоскедастичности, или
равноизменчивости случайной составляющей (возмущения).
Чтобы
проверить выполняется то условие или нет, применим тест Голдфельда-Квандта.
Шаг 1. Упорядочим n наблюдений по мере возрастания
переменной x.
Шаг 2. Разделим совокупность на две группы
и определим по каждой из групп уравнения регрессии. 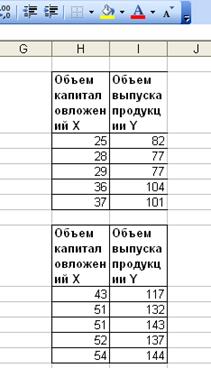
Рис. 7.
Деление совокупности на две группы
Определим
по каждой из групп уравнения регрессии помощью инструмента Анализа данных
Регрессия. Заполним диалоговое окно для первой группы:
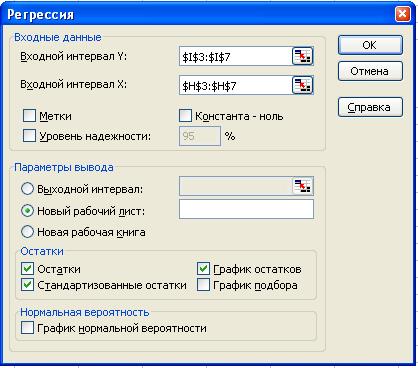
Рис. 8.
Регрессия (первая группа)
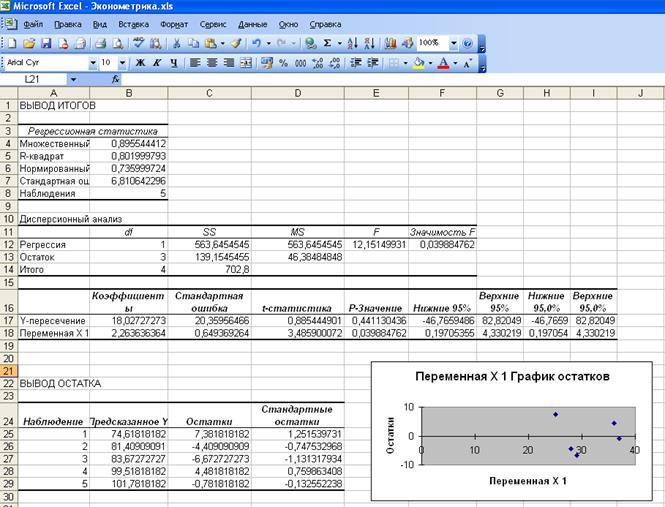
Рис. 9.
Вывод итогов для первой группы
В
ячейках В17 и В18 на Листе 2 (рис. 9) расположены значения параметров а и b соответственно. Итак, уравнение
регрессии первой группы имеет вид:
ŷ1 = 18,02+2,26X.
Заполним
диалоговое окно для второй группы:
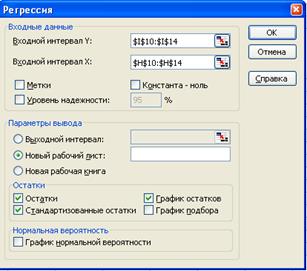
Рис. 10.
Регрессия (вторая группа)
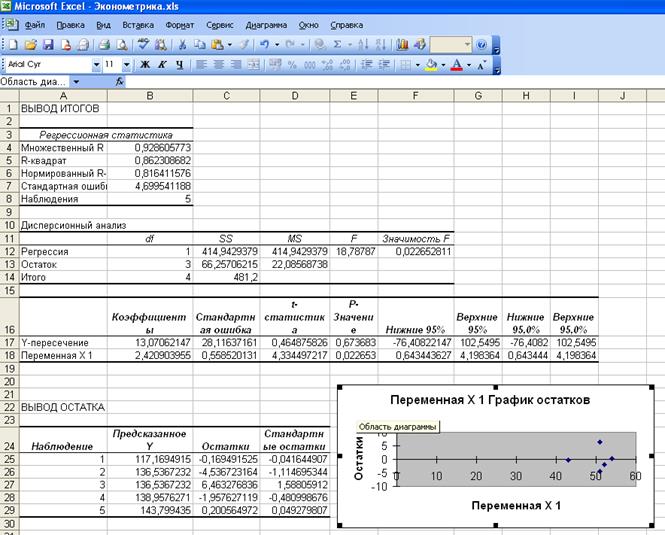
Рис. 11.
Вывод итогов для второй группы
В
ячейках В17 и В18 на Листе 3 (рис. 11) расположены значения параметров а и b соответственно. Итак, уравнение
регрессии второй группы имеет вид:
ŷ2 = 13,07+2,42·x.
Шаг 3. Определим остаточную сумму квадратов для первой
регрессии:
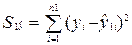
Остаточная
сумма квадратов для первой регрессии уже вычислена с помощью инструмента
Анализа Данных - Регрессии и равна 139,15
(рис. 9, ячейка С 13).
Остаточная
сумма квадратов для второй регрессии определяется по формуле:
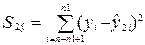 .
.
Остаточная
сумма квадратов для второй регрессии тоже уже вычислена с помощью инструмента
Анализа данных и равна 66,26 ( рис. 11,
ячейка С 13).
Таким образом, 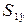 =139,15;
=139,15; 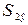 =66,26.
Шаг 4. Вычислим наблюдаемое значение F-критерия Фишера, как отношение
величин:
=66,26.
Шаг 4. Вычислим наблюдаемое значение F-критерия Фишера, как отношение
величин: 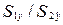 (или
(или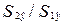 ).
).
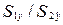 =139,15/66,26=2,1
=139,15/66,26=2,1
Шаг 5. F - наблюдаемое сравним с F – табличным. F-наблюдаемое уже вычислено и
составляет 2,1.
Табличное
значение F-критерия Фишера при доверительной вероятности 0,05 при ν1=1 и ν2=8
можно найти с помощью функции FРАСПОБР.

Рис. 12.
Результаты вычислений
Итак, 2,1<5,32
(F набл <F табл). Следовательно, гомоскедастичность
имеет место, т.е данное условие выполняется.
Условие 5. Предположение о нормальности
распределения случайного члена. Проверим его с помощью R/S-критерия, который находиться по
формуле:
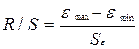 , где
, где 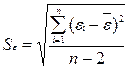 .
.
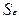 уже вычислено с
помощью инструмента Анализа данных Регрессии и составляет 5,09 (стр. 4, рис. 3,
ячейка B7), а εmax= 8,066 и εmin=-6,540. Тогда
уже вычислено с
помощью инструмента Анализа данных Регрессии и составляет 5,09 (стр. 4, рис. 3,
ячейка B7), а εmax= 8,066 и εmin=-6,540. Тогда
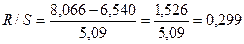 .
.
Итак, RS-критерий равен 0,299. Т.к. RS-критерий не попадает в интервал от
2,7 до 3,7 , то, следовательно, остатки не отвечают нормальному закону
распределения.
Задача 4.
Осуществим проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (α=0,05): 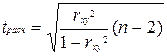 .
.
Значения
t-критерия
вычисляются по формулам: 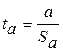 ;
; 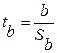 .
.
Данные значения ta и tb уже вычислены с помощью Регрессии
(рис. 3) – ячейки D17 и D18 соответственно и составляют ta= 2,158; tb = 15,648. Рассчитаем табличное
значение t-критерия Стьюдента (α=0,05) с помощью функции СТЬЮДРАСПОБР.
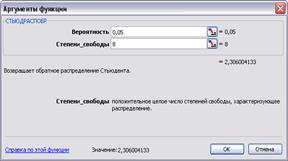
Рис. 14. Аргументы функции СТЬЮДРАСПОБР
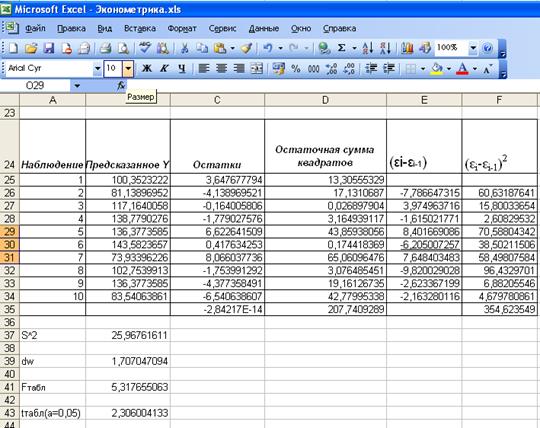
Рис. 15. Результат вычисления
Итак,
табличное значение t-критерия при 5% - ном уровне
значимости и степенях свободы составляет 2,306. Так как tа>tтабл и tb>tтабл, то параметры a и b уравнения регрессии значимы.
Осуществим
проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (α=0,1) с
помощью функции СТЬЮДРАСПОБР.

Рис. 16. Результат вычисления tтабл (α=0,1)
Итак, табличное значение t-критерия при уровне значимости и
степенях свободы составляет 1,859548033. Так как tа>tтабл и tb>tтабл, то параметры a и b уравнения регрессии значимы.
Задача 5.
В случае линейной зависимости между переменными парный коэффициент корреляции
является показателем тесноты связи и определяется по формуле:
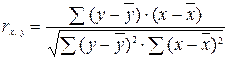 .
.
Коэффициент корреляции в
нашем примере уже вычислен с помощью инструмента Excel
Регрессии (рис. 3, стр. 4) – ячейка В4, который равен 0,98405.
По шкале Чеддока коэффициент
корреляции попал в интервал от 0,9 до 1, следовательно, это говорит о весьма
высокой связи.
Долю дисперсии, объясняемую регрессией в общей
дисперсии результативного признака y, характеризует коэффициент
детерминации:
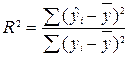 .
.
Коэффициент детерминации
в нашем примере уже вычислен с помощью инструмента анализа Регрессии (рис. 3,
ячейка В5) и составляет 0,96836.
Значимость уравнения регрессии y=13,89+2,40x определяется с помощью F-критерия Фишера (α=0,05)
используя данную формулу: 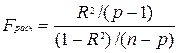 .
.
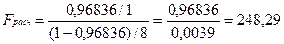 .
.
Табличное значение F-критерия Фишера при доверительной
вероятности 0,05 при ν1=1
и ν2=8 уже вычислено с помощью функции FРАСПОБР и составляет 5,31766.
Поскольку Fрасч>F табл, уравнение регрессии следует
признать значимым.
Коэффициент
эластичности для линейной функции
определяется по формуле:
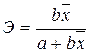 .
.
Таким
образом, 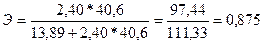 .
.
Это
значит, что если фактор измениться на 1%, то в среднем на 0,87% измениться
результат.
Чтобы
иметь общее суждение о качестве модели из относительных отклонений по каждому
наблюдению, определяют относительную ошибку аппроксимации:
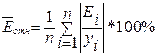 .
.
Вычислим
относительную ошибку аппроксимации с помощью Excel.
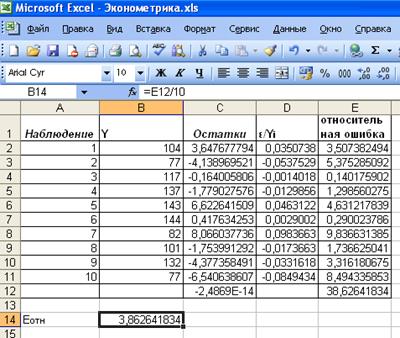
Рис.17. Результаты вычислений относительной ошибки аппроксимации
Итак,
относительная ошибка аппроксимации составила 3,86%, что говорит о качественной
модели.
Задача 6.
Осуществим прогнозирование среднего значения показателя Y при уровне значимости α=0,1,
если известно, что прогнозное значение фактора Х составит 80% от его
максимального значения.
Прогнозное
значение переменной y получается при подстановке в уравнение регрессии ожидаемого значения x: 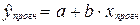 , где
, где 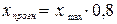 .
.
В
нашем случае 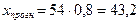 .Отсюда
.Отсюда 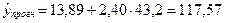 .
.
Вероятность
реализации точечного прогноза равна нулю. Поэтому рассчитывается средняя ошибка
прогноза или доверительный интервал прогноза с достаточно большей надежностью.
Доверительные интервалы зависят от стандартной ошибки, удаления 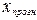 от своего среднего
значения
от своего среднего
значения 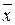 , количества наблюдений n и уровня значимости прогноза α.В частности, для
прогноза будущие значения
, количества наблюдений n и уровня значимости прогноза α.В частности, для
прогноза будущие значения 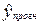 с вероятностью
(1-α) попадут в интервал:
с вероятностью
(1-α) попадут в интервал:
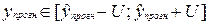 .
.
Ширина
доверительного интервала определяется по формуле:
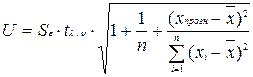 .
.
Величина 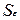 уже вычислена (рис. 3,
ячейка В7) и равна 5,0958. Коэффициент Стьюдента
уже вычислена (рис. 3,
ячейка В7) и равна 5,0958. Коэффициент Стьюдента 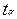 для m=8 степеней свободы и уровня
значимости 0,1 равен 1,859548033 Произведем дополнительные расчеты:
для m=8 степеней свободы и уровня
значимости 0,1 равен 1,859548033 Произведем дополнительные расчеты:
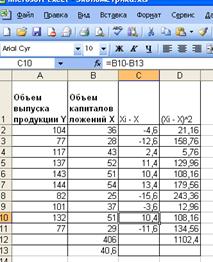
Рис. 18.
Дополнительные расчеты
Тогда:
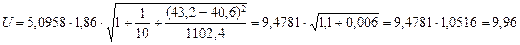 .
.
Итак,
получены границы:
Таблица 2.
|
Нижняя граница
|
Прогноз
|
Верхняя граница
|
|
107,58
|
117,57
|
127,5
|
Задание 7. Представим графически фактические и
модельные значения Y точки прогноза, а для этого построим таблицу.
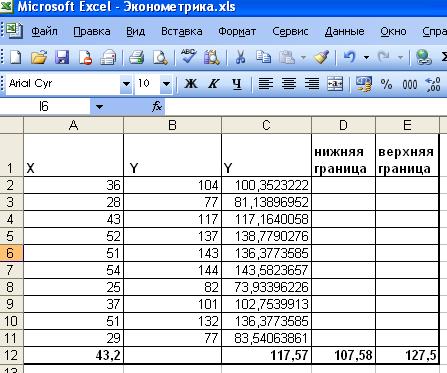
Рис. 20. Дополнительная таблица
Упорядочим значения по X по возрастанию и в результате
получим:
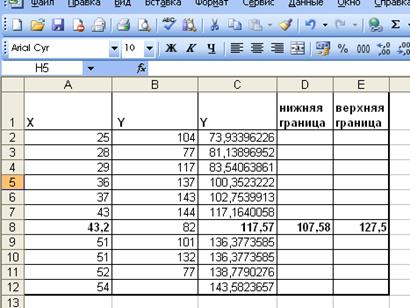
Рис. 21. Сортировка по возрастанию Х
С помощью Мастер диаграмм
я получила график:
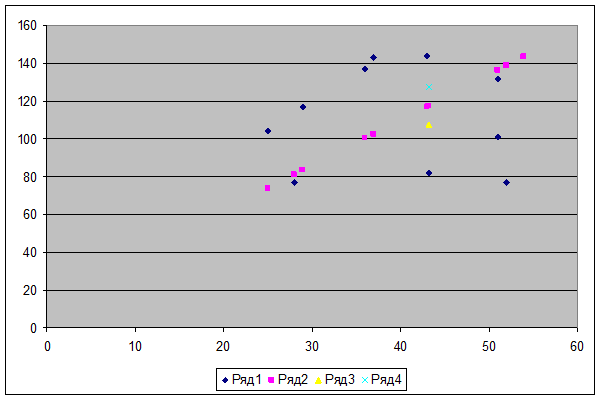
Рис. 22. Диаграмма
Где ряд1-Y,ряд2-Y,ряд 3-нижняя граница,ряд4-верхняя граница.
Задание 8.
а) Составим
уравнение гиперболической модели
парной регрессии.
Уравнение гиперболической функции
имеет вид: 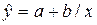 .
.
Произведем линеаризацию
модели путем замены Х=1/х. В результате получим линейное уравнение: 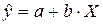 . Рассчитаем его параметры по формулам:
. Рассчитаем его параметры по формулам:
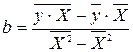 ;
; 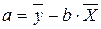 .
.
Построим дополнительную таблицу и
произведем расчеты.
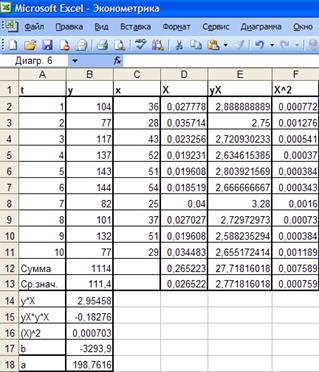
Рис. 22.
Результаты вычислений параметров гиперболической функции
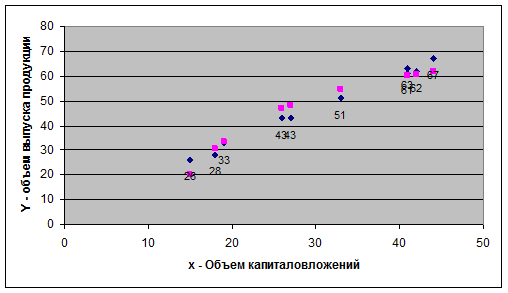
Рис. 23.
гиперболическая функция
Итак, b = -3293,9 и а = 198,7616. Получим
следующее уравнение гиперболической модели: 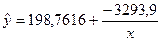 .
.
б) Уравнение степенной модели имеет вид: 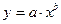 . Для построения этой модели необходимо произвести
линеаризацию переменных. Для этого произведем логарифмирование обеих частей
уравнения:
. Для построения этой модели необходимо произвести
линеаризацию переменных. Для этого произведем логарифмирование обеих частей
уравнения: 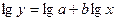 .
.
Пусть Y=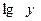 , Х=
, Х=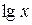 , А=
, А=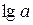 , тогда уравнение примет вид Y=A+bX – линейное уравнение регрессии.
Рассчитаем его параметры по формулам:
, тогда уравнение примет вид Y=A+bX – линейное уравнение регрессии.
Рассчитаем его параметры по формулам:
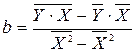 ;
; 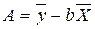 .
.
Построим дополнительную таблицу и произведем расчеты.
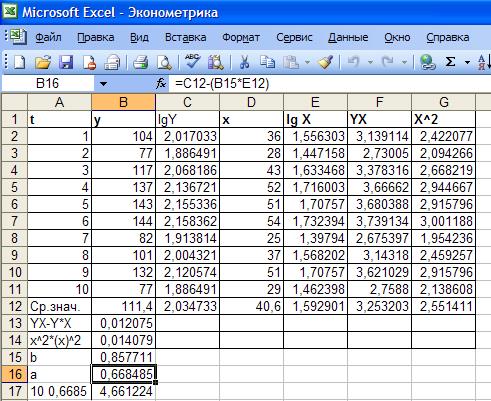
Рис. 23. Результаты вычислений
степенной модели
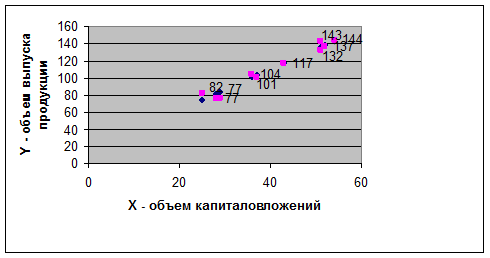
Рис. 24. Степенная функция
Итак, b = 0,8577А = 0,6684 (рис. 23, ячейки
В15 В 16 соответственно). В результате уравнение регрессии имеет вид: Y=0,6684-0,8577·Х. перейдем к исходным
переменным x и y, выполнив потенцирование данного уравнения: 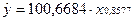 .
.
Получим
уравнение степенной модели регрессии: 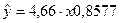 .
.
в) Уравнение показательной
кривой имеет вид:  . Для построения этой модели необходимо произвести
линеаризацию переменных. Для этого осуществим логарифмирование обеих частей
уравнения:
. Для построения этой модели необходимо произвести
линеаризацию переменных. Для этого осуществим логарифмирование обеих частей
уравнения: 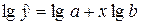 .
.
Пусть Y=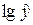 , В=
, В=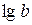 , А=
, А=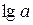 , тогда уравнение регрессии примет вид: Y=A+Bx.
, тогда уравнение регрессии примет вид: Y=A+Bx.
Построим дополнительную таблицу и
произведем расчеты.
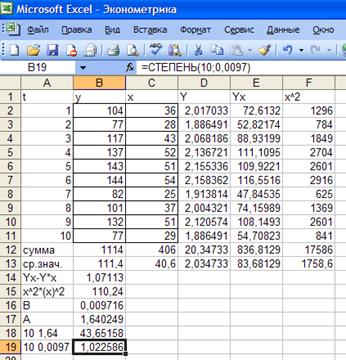
Рис. 24. Результаты вычислений параметров
показательной функции
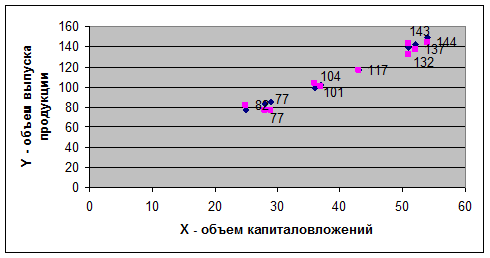
Рис. 25 Показательная функция
Итак, В=0,0097 и А=1,64
(рис. 24, ячейки В16 и В17 соответственно). Уравнение регрессии имеет вид: Y=1,64 + 0,0097·х. перейдем к исходным
переменным х и у, выполнив потенцирование данного уравнения: 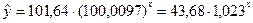 .
.
Задача 9.
Найдем коэффициенты детерминации для данных моделей по формуле:
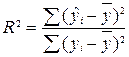 .
.
Но при этом вычислим индекс
корреляции для каждой модели:
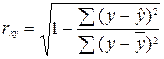 .
.
А также нужно найти
коэффициенты эластичности для каждого типа уравнения регрессии. И для
определения качества каждой модели найдем средние относительные ошибки
аппроксимации, которые определяются по формуле:
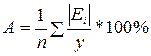 .
.
а) Для гиперболической функции.
Проведем дополнительные
расчеты.
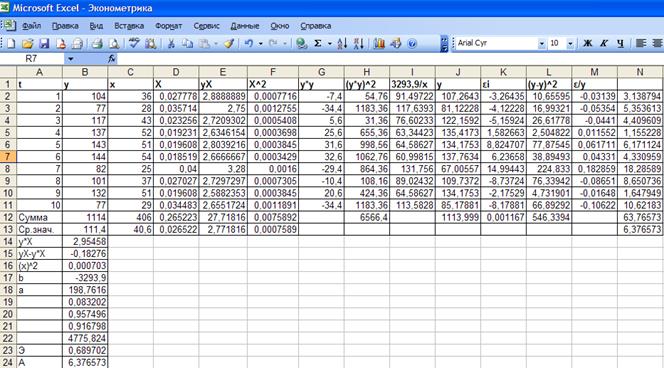
Рис. 26.
Результаты вычислений
Итак, индекс корреляции
равен 0,9574 (рис. 26, ячейка В20). Связь между показателем у и фактором х
высокая.
Индекс детерминации равен
0,9167 (рис. 26, ячейка В21). Вариация результата Y (объема выпуска продукции) на 91,67%
объясняется вариацией фактора Х (объемом капиталовложений).
Коэффициент
эластичности для гиперболической функции определяется по формуле: 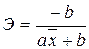 . В нашем случае он равен 0,6897 (рис. 26, ячейка 23). Это
значит, что если фактор измениться на 1%, то в среднем на 0,68% измениться
результат.
. В нашем случае он равен 0,6897 (рис. 26, ячейка 23). Это
значит, что если фактор измениться на 1%, то в среднем на 0,68% измениться
результат.
Относительная ошибка
аппроксимации гиперболической функции равна 6,3765% (рис. 26, ячейка B24), что говорит о некачественной
модели.
б)
Для степенной функции.
Проведем дополнительные
расчеты.
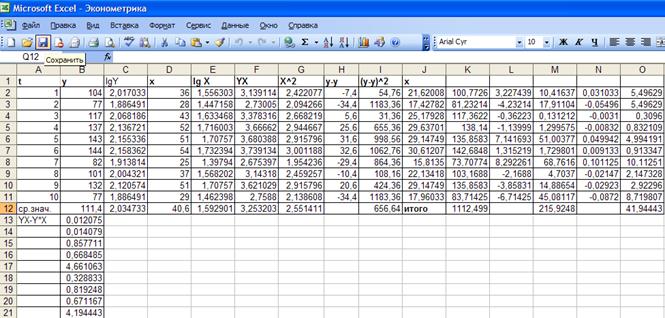
Рис. 27.
Результаты вычислений
Итак, индекс корреляции
равен 0,8192 (рис. 27, ячейка В19). Связь между показателем у и фактором х
весьма высокая.
Индекс детерминации равен
0,6711 (рис. 27, ячейка В20). Вариация результата Y (объема выпуска продукции) на 67,11%
объясняется вариацией фактора Х (объемом капиталовложений).
Коэффициент
эластичности для степенной функции находиться по формуле: Э=b, следовательно, коэффициент
эластичности степенной функции равен 0,85 (ячейка В15). Это значит, что если
фактор измениться на 1%, то в среднем на 0,85% измениться результат.
Относительная ошибка
аппроксимации степенной функции равна 4,1944% (рис. 27, ячейка B21), что говорит о качественной
модели.
в)
Для показательной функции.
Проведем дополнительные
расчеты.
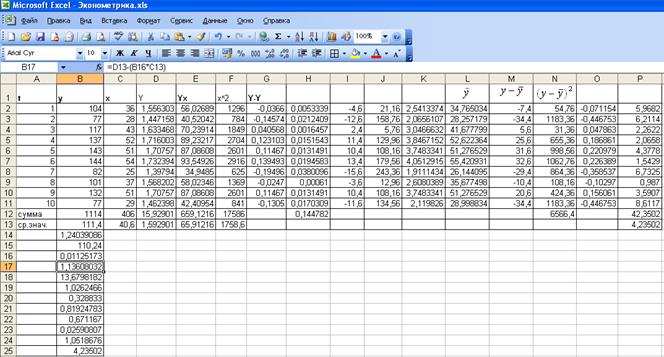
Рис. 28.Результаты
вычислений
Итак, индекс корреляции
равен 0,8192 (рис. 28, ячейка В21). Связь между показателем у и фактором х
весьма высокая.
Индекс детерминации равен
0,6711 (рис. 28, ячейка В22). Вариация результата Y (объема выпуска продукции) на 67,11%
объясняется вариацией фактора Х (объемом капиталовложений).
Коэффициент
эластичности для показательной функции определяется по формуле: 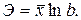 В нашем случае он
равен 1,0518(рис. 28, ячейка B24). Это значит, что если фактор измениться на 1%, то в среднем
на 1,05% измениться результат.
В нашем случае он
равен 1,0518(рис. 28, ячейка B24). Это значит, что если фактор измениться на 1%, то в среднем
на 1,05% измениться результат.
Относительная ошибка
аппроксимации показательной функции равна 4,2350% (рис. 28, ячейка B25), что говорит о качественной
модели.
Сравним
модели по этим характеристикам.
|
модель
|
|
Еотн
ср
|
R-квадрат
|
|
линейная
|
3,86
|
0,968
|
|
гиперболическая
|
6,38
|
0,917
|
|
степенная
|
3,96
|
0,967
|
|
показательная
|
4,24
|
0,967
|
Вывод: Самое хорошее качество имеет степенная
модель. Коэффициент детерминации R²
наиболее близок к 1 у степенной модели. (вариация объема
капиталовложений на 96,7117% объясняет вариацию выпуска продукции) и наименьшая
средняя относительная ошибка аппроксимации 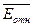 = 3,955%.. Степенная
модель из трех представленных моделей лучше всего описывает исходные данные.
= 3,955%.. Степенная
модель из трех представленных моделей лучше всего описывает исходные данные.