Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

ГОУ ВПО

Всероссийский заочный финансово-экономический институт

Кафедра экономико-математических методов и моделей

КОНТРОЛЬНАЯ РАБОТА

по дисциплине «Финансовая математика»

Вариант № 8

     

Исполнитель:

Специальность:

Группа:

№ зачетной книжки:

Руководитель:

МОСКВА

2008

 

Задание 1

В табл. 1.1 представлены следующие данные

Таблица 1.1

t	1	2	3	4	5	6	7	8	9
Y(t)	85	81	78	72	69	70	64	61	56

1.   Оценить точность построенной модели с использованием средней относительной ошибки аппроксимации;

2.   Оценить адекватность построенной модели на основе исследования:

·        случайности остаточной компоненты по критерию пиков;

·        независимости уровней ряда остатков по d-критерию (критические значения d₁ = 1,10 и d₂ = 1,37) и по первому коэффициенту автокорреляции при критическом значении  r₁ = 0,32;

·  нормальности распределения остаточной компоненты по R/S-критерию с критическими значениями от 3 до 4,21.

3.   Построить точечный прогноз на 4 шага вперед.

4.   Отобразить на графиках фактические, расчетные и прогнозные данные.

Решение

Для оценки начальных значений а(0) и b(0) применим линейную модель к значениям Y(t). Линейная модель имеет вид:

 

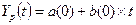
Метод наименьших квадратов дает возможность определить коэффициенты линейного уравнения   по формулам:

 

 

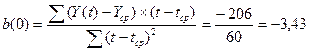
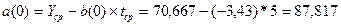
Таблица 1.2

	t	y(t)
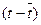
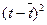
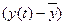
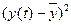
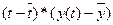
1	85	-4	16	14,3333	205,4444	-57,3333
2	81	-3	9	10,3333	106,7778	-31,0000
3	78	-2	4	7,3333	53,7778	-14,6667
4	72	-1	1	1,3333	1,7778	-1,3333
5	69	0	0	-1,6667	2,7778	0,0000
6	70	1	1	-0,6667	0,4444	-0,6667
7	64	2	4	-6,6667	44,4444	-13,3333
8	61	3	9	-9,6667	93,4444	-29,0000
9	56	4	16	-14,6667	215,1111	-58,6667
Сумма	45	636	0	60	0,0000	724,0000	-206,0000
Среднее	5	70,6667

Произведем расчет:

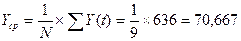
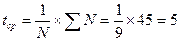
Уравнение с  учетом полученных коэффициентов имеет вид:

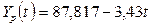
Для сопоставления фактических данных Y(t) и рассчитанных по линейной модели значений Y_p(t) составим таблицу (табл. 1.3).

Таблица 1.3

t	1	2	3	4	5	6	7	8	9
Y(t)	85	81	78	72	69	70	64	61	56
Yp(t)	84,387	80,957	77,527	74,097	70,667	67,237	63,807	60,377	56,947

         Зависимость между компонентами тренд – сезонный временный ряд мультипликативная. Мультипликативная модель Хольта-Уинтерса с линейным ростом имеет следующий вид:

,

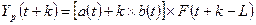где    k – период упреждения;

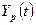 - расчетное значение экономического показателя для t-го периода;

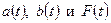 - коэффициенты модели;

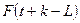 - значение коэффициента сезонности того периода, для которого рассчитывается экономический показатель;

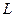 - период сезонности.

 Уточнение коэффициентов модели производится с помощью формул:

a(t) = α₁  * Y(t)/F(t-L) + (1-α₁) * [a(t-1)+b(t-1)];

b(t) = α₃ * [a(t)-a(t-1)] + (1-α₃) * b(t-1);

F(t) = α₂ * Y(t)/a(t) + (1-α₂) * F(t-L)

         Параметры сглаживания равны:

α₁ = 0,3

α₂ = 0,6

α₃ = 0,3

Построение модели Хольта-Уинтерса.

	t	Y(t)	a(t)	b(t)	F(t)	Yp(t)
-3				0,99184
-2				1,02081
-1				1,00456
0		87,817	-3,43	0,99101
1	85	84,78076	-3,31187	0,99829	84,387
2	81	80,83280	-3,50270	1,02081	80,957
3	78	77,42478	-3,47429	1,00456	77,527
4	72	73,56131	-3,59105	0,99101	74,097
5	69	69,71471	-3,66771	0,99829	70,667
6	70	66,80475	-3,44039	1,02081	67,237
7	64	63,46785	-3,40934	1,00456	63,807
8	61	60,50698	-3,27480	0,99101	60,377
9	56	56,89137	-3,37704	0,99829	56,947
	10					54,628
	11					50,366
	12					46,3398
	13					43,3089
Сумма	45	636
Среднее	5	70,66667

Проверка качества модели.

Для того чтобы модель была качественной уровни, остаточного ряда E(t) (разности 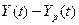 между фактическими и расчетными значениями экономического показателя) должны удовлетворять определенным условиям (точности и адекватности). Для проверки выполнения этих условий составим таблицу 1.4.

     Таблица 1.4

Промежуточные расчеты для оценки адекватности модели

	t	E(t)	Точка поворота	E(t)2	[E(t)-E(t-1)]	[E(t)-E(t-1)]2	E(t)*E(t-1)
1	0,613	-	0,375769	-	-	-
2	0,043	1	0,001849	-0,57	0,3249	0,026359
3	0,473	1	0,223729	0,43	0,1849	0,020339
4	-2,097	1	4,397409	-2,57	6,6049	-0,991881
5	-1,667	0	2,778889	0,43	0,1849	3,495699
6	2,763	1	7,634169	4,43	19,6249	-4,605921
7	0,193	1	0,037249	-2,57	6,6049	0,533259
8	0,623	1	0,388129	0,43	0,1849	0,120239
9	-0,947	-	0,896809	-1,57	2,4649	-0,589981
Сумма	45	-0,003	6	16,734001	-1,56	36,1792	-1,991888

Проверка точности модели.

Рассчитаем среднюю относительную ошибку аппроксимации

Таблица 1.5

	t	Y(t)	Yp(t)	Е(t)	Абс.Ошибка	Относ.Ошибка,%
1	85	84,387	0,613	0,613	0,7212
2	81	80,957	0,043	0,043	0,0531
3	78	77,527	0,473	0,473	0,6064
4	72	74,097	-2,097	2,097	2,9125
5	69	70,667	-1,667	1,667	2,4159
6	70	67,237	2,763	2,763	3,9471
7	64	63,807	0,193	0,193	0,3016
8	61	60,377	0,623	0,623	1,0213
9	56	56,947	-0,947	0,947	1,6911
Сумма	45	636		-0,003	9,419	13,6702
Среднее	5	70,6667			1,0466	1,51891

Будем считать, что условие точности выполнено, если относительная погрешность (абсолютное значение отклонения abs{E(t)}, поделенное на фактическое значение Y(t) и выраженное в процентах 100%* abs{E(t)}/ Y(t) в среднем не превышает 5%. Суммарное значение относительных погрешностей составляет 13,6702, что дает среднюю величину 13,6702/9 = 1,51891%, что не превышает 5%.

Следовательно, условие точности выполнено.

 

Проверка условия адекватности.

Для того чтобы модель была адекватна исследуемому процессу, ряд остатков E(t) должен обладать свойствами случайности, независимости последовательных уровней, нормальности распределения.

Проверка случайности уровней. Проверку случайности уровней остаточной компоненты (гр. 3 табл. 1.4) проводим на основе критерия поворотных точек. Для этого каждый уровень ряда Е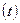 сравниваем с двумя соседними. Если он больше (либо меньше) обоих соседних уровней, то точка считается поворотной и в гр. 4 табл. 1.4 для этой строки ставится 1, в противном случае в гр. 4 ставится 0. В первой и в последней строке гр. 4 табл. 1.4 ставится прочерк или иной знак, так как у этого уровня нет двух соседних уровней.

Общее число поворотных точек в нашем примере равно  р=6.

Рассчитаем значение :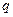

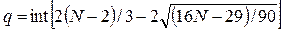
Функция int означает, что от полученного значения берется только целая часть. При N = 9.

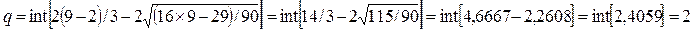
Так как количество поворотных точек р=6 больше q=2, то условие случайности уровней ряда остатков выполнено.

Проверка независимости уровней ряда остатков (отсутствия автокорреляции).

Проверку проводим по d-критерию критерий Дарбина-Уотсона (критические уровни d₁=1,10 и  d₂=1,37):

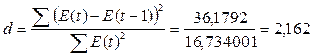
Так как полученное значение больше 2, то величину d уточним:

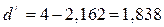
d2<d<2, таким образом в нашем примере 1,37<1,838<2, следовательно уровни ряда остатков являются независимыми.

Это значение не попадает в критический интервал, ряд остатков не коррелирован.

Предпосылка выполнена.

Проверка соответствия ряда остатков нормальному распределению определяем по RS-критерию. Рассчитаем значение RS:

,

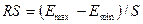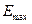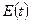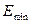где     - максимальное значение уровней ряда остатков ;

 - минимальное значение уровней ряда остатков  ;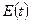

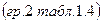S – среднее квадратическое отклонение.

;

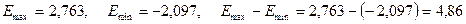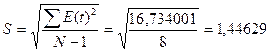
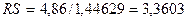
Так как 3,00<3,3603<4,21, полученное значение RS попало в заданный интервал. Значит, уровни ряда остатков подчиняются нормальному распределению.

Таким образом, все условия адекватности и точности выполнены, и можно утверждать, что данная модель является качественной.

 

Расчет прогнозных значений экономического показателя.

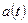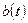Составим прогноз на четыре шага вперед (т.е.  с t=10 по t=13). Максимальное значение t, для которого могут быть рассчитаны коэффициенты  и  определяется количеством исходных данных и равно 9. Рассчитав значения 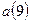 и 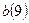 (см. табл. 1.4) по формуле:

,

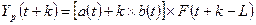где    k – период упреждения;

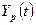 - расчетное значение экономического показателя для t-го периода;

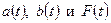 - коэффициенты модели;

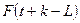 - значение коэффициента сезонности того периода, для которого рассчитывается экономический показатель;

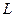 - период сезонности.

Определим прогнозные значения экономического показателя Y_p(t) для: t = 10, 11, 12 и 13.

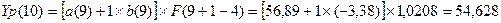
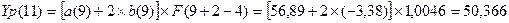
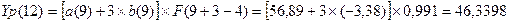
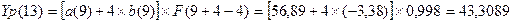
На нижеприведенном рисунке проводится сопоставление фактических и расчетных данных. Здесь же показаны прогнозные значения на   4 шага вперед. Из рисунка видно, что расчетные данные хорошо согласуются с фактическими, что говорит об удовлетворительном качестве прогноза.

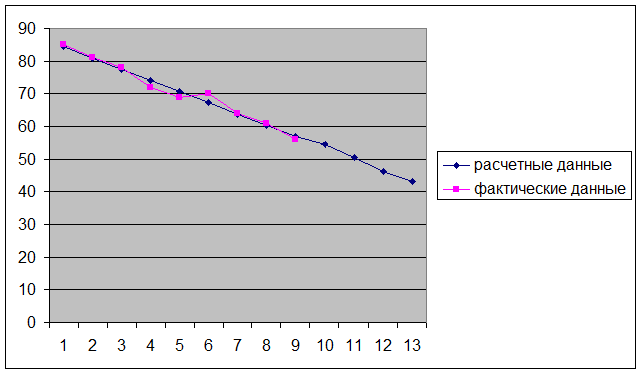
Рис. 1. Сопоставление расчетных  и фактических  данных

Задание 2

В таблице 2.1 даны цены (открытия, максимальная, минимальная и закрытия) за 10 дней. Интервал сглаживания принять равным 5 дням.

Рассчитать:

·        экспоненциальную скользящую среднюю;

·        момент;

·        скорость изменения цен;

·        индекс относительной силы;

·        % R, % К, % D;

Расчеты проводить для всех дней, для которых эти расчеты можно выполнить на основании имеющихся данных.

Таблица 2.1

Дни	Цены
макс.	мин.	закр.
1	600	550	555
2	560	530	530
3	536	501	524
4	545	521	539
5	583	540	569
6	587	562	581
7	582	561	562
8	573	556	573
9	610	579	592
10	645	585	645

Решение

Для расчета экспоненциальной скользящей средней воспользуемся формулой:

,

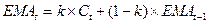где    k = 2 / (n + 1),

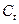          - цена закрытия t-го дня;

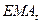          - значение EMA текущего дня t.

Момент рассчитывается как разница конечной цены текущего дня 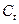 и цены n дней тому назад :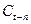

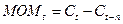
где 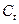    - цена закрытия t-го дня.

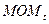          - значение МОМ текущего дня t.

Скорость изменения цен рассчитываем как отношение конечной цены текущего дня к цене n дней тому назад, выраженное в процентах:

,

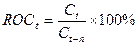где 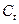    - цена закрытия t-го дня.

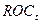          - значение ROC текущего дня t.

Результаты расчетов представим в таблице (табл. 2.2).

Таблица 2.2

 

Дни	Цена закрытия	Экспоненциальная скользящая средняя EMAt	Момент          MOM	Скорость изменения цен  ROC	Повышение цены	Понижение цены	Сумма повышений	Сумма понижений	Индекс относительной силы RSI
1	555	-	-	-	-	-	-	-	-
2	530	-	-	-	-	25	-	-	-
3	524	-	-	-	-	6	-	-	-
4	539	-	-	-	15	-	-	-	-
5	569	543,4000	-11,6000	102,5225	30	-	-	-	-
6	581	555,9333	25,9333	109,6226	12	-	57	31	64,77
7	562	557,9555	33,9555	107,2519	-	19	57	25	69,51
8	573	562,9704	23,9704	106,308	11	-	68	19	78,16
9	592	572,6469	3,6469	104,0422	19	-	72	19	79,12
10	645	596,7646	15,7646	111,0155	53	-	95	19	83,33

K = 2/(n+1)= 2/6=0,33333

Для расчета индекса относительной силы используем формулу:

,

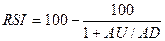где    AU – сумма приростов конечных цен за n последних дней;

         AD – сумма убыли конечных цен за n последних дней.

Рассчитаем  %R,  %К,  %D используя следующие формулы:

,

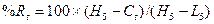где 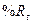    - значение индекса текущего дня t;

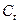          - цена закрытия t-го дня;

L₅ и Н₅ – минимальная и максимальные цены за n предшествующих дней, включая текущие.

,

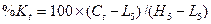где 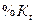    - значение индекса текущего дня t;

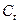          - цена закрытия t-го дня;

L₅ и Н₅ – минимальная и максимальная цены за 5 предшествующих дней, включая текущие.

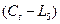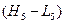Индекс %D рассчитывается аналогично индексу %К, с той лишь разницей, что при его построении величины  и   сглаживают, беря их трехдневную сумму.

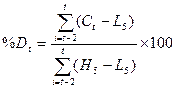
Результаты расчетов представим в таблице 2.3

 

 

 

Таблица 2.3

Дни t	Максимальная цена за день Ht	Минимальная цена за день Lt	Цена закрытия Ct	Максимальная цена за 5 дней H5	Минимальная цена за 5 дней L5	Ct-L5	H5-L5	H5-Ct	% K	% R	Сумма за 3 дня  Ct-L5	Сумма за 3 дня  H5-L5	% D	Медленное % D
1	600	550	555	-	-	-	-	-	-	-	-	-	-	-
2	560	530	530	-	-	-	-	-	-	-	-	-	-	-
3	536	501	524	-	-	-	-	-	-	-	-	-	-	-
4	545	521	539	-	-	-	-	-	-	-	-	-	-	-
5	583	540	569	600	501	68	99	31	68,687	31,313	-	-	-	-
6	587	562	581	587	501	80	86	6	93,023	6,977	-	-	-	-
7	582	561	562	587	501	61	86	25	70,930	29,070	209	271	77,122	-
8	573	556	573	587	521	52	66	14	78,788	21,212	193	238	81,092	-
9	610	579	592	610	540	52	70	18	74,286	25,714	165	222	74,324	77,513
10	645	585	645	645	556	89	89	0	100,000	0,000	193	225	85,778	80,398

Задание 3

3.1. Банк выдал ссуду, размером 3 000 000 руб. Дата выдачи ссуды 14.01.02, возврата 18.03.02. День выдачи и день возврата считать за 1 день. Проценты рассчитываются по простой процентной ставке 35% годовых. Найти:

3.1.1) точные проценты с точным числом дней ссуды;

3.1.2) обыкновенные проценты с точным числом дней ссуды;

3.1.3) обыкновенные проценты с приближенным числом дней ссуды.

Решение

3.1.1) К = 365, t = 64, I = 3000000 * 0,35 * 64 / 365 = 184 109,59  руб.

3.1.2) К = 360, t = 64, I = 3000000 * 0,35 * 64 / 360 = 186 666,67  руб.

3.1.3) К = 360, t = 65, I = 3000000 * 0,35 * 65 / 360 = 189 583,33  руб.

3.2. Через 90 дней после подписания договора должник уплатил       3 000 000 руб. Кредит выдан под 35% годовых (проценты обыкновенные). Какова первоначальная сумма и дисконт?

Решение

P = S / (1 + ni) = 3000000 / (1 + 0,35 * 90 / 360) = 2 758 620,69 руб.

D = S – P = 3000000 – 3595505,62 = 241 379,31 руб.

3.3. Через 90 предприятие должно получить по векселю 3 000 000 руб. Банк приобрел этот вексель с дисконтом. Банк учел вексель по учетной ставке 35% годовых (год равен 360 дням). Определить полученную предприятием сумму и дисконт.

Решение

D = S_nd = 3000000 * 0,35 * 90 / 360 = 262 500,00 руб.

P = S – D = 3000000 – 262500,00 = 2 737 500,00 руб.

3.4. В кредитном договоре на сумму 3 000 000 руб. и сроком на 5 лет, зафиксирована ставка сложных процентов, равная 35% годовых. Определить наращенную сумму.

Решение

S = P * (1+i)ⁿ = 3000000 * (1 + 0,35)⁵ = 13 452 100,31 руб.

3.5. Ссуда, размером 3 000 000 руб. представлена на 5 лет. Проценты сложные, ставка 35% годовых. Проценты начисляются 4 раза в году. Вычислить наращенную сумму.

Решение

N = 5 * 4 = 20

S = P * (1+j / m)^N  =3000000 * (1 + 0,35 / 4)²⁰  = 16 058 558,84 руб.

3.6. Вычислить эффективную ставку процентов, если банк начисляет проценты 4 раза в год, исходя из номинальной ставки 35% годовых.

Решение

i_э = (1 + j / m)^m - 1 = (1 + 0,35 / 4)⁴ – 1 = 0,3987, т.е. 39,87%.

3.7. Определить, какой должна быть номинальная ставка при начислении процентов 4 раза в году, чтобы обеспечить эффективную ставку 35% годовых.

Решение

j = m * [(1 + i_э)^1/m - 1] = 4 * [(1 + 0,35)^(1/4) – 1] = 0,3116, т.е. 31,16%.

3.8. Через 5 лет предприятию будет выплачена сумма 3 000 000 руб. Определить ее современную стоимость при условии, что применяется сложная процентная ставка 35% годовых.

Решение

 

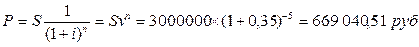
3.9. Через 5 лет по векселю должна быть выплачена сумма 3 000 000 руб. Банк учел вексель по учетной ставке 35% годовых. Определить дисконт.

Решение

P = S (1 – d_сл)ⁿ = 3000000 * (1 – 0,35)⁵ = 348 087,19 руб.

D = S – P = 3000000 – 201313,75 = 2 651 912,81 руб.

3.10. В течение 5 лет на расчетный счет в конце каждого года поступает по 3 000 000 руб., на которые 4 раза в году начисляются проценты по сложной годовой ставке 35%. Определить сумму на расчетном счете к концу указанного срока.

Решение