Задача № 1

Металлургическому заводу требуется уголь с содержанием фосфора не более 0,03% и с долей зольных примесей не более 3,25%. Завод закупает три сорта угля – А, В, С с известным содержанием примесей. В какой пропорции нужно смешивать исходные продукты А,В,С, чтобы смесь удовлетворяла ограничениям на содержание примесей и имела минимальную цену? Содержание примесей и цена исходных продуктов приведены в таблице.

Сорт угля	Содержание (%)	Цена 1 т (руб.)
фосфора	золы
А	0,06	2,0	30
В	0,04	4,0	30
С	0,02	3,0	45

Экономико-математическая модель задачи

f(x) = 30x₁ + 30x₂ + 45x₃   → min

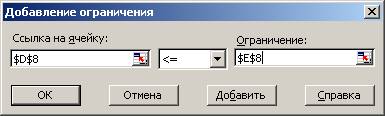
0,06x₁ + 0,04x₂ + 0,02 x₁ ≤ 0,03

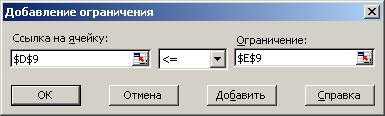
2x₁ + 4x₂ + 3 x₁ ≤ 3,25

Решение

1 Вводим исходные данные

2. Вводим зависимость для целевой функции

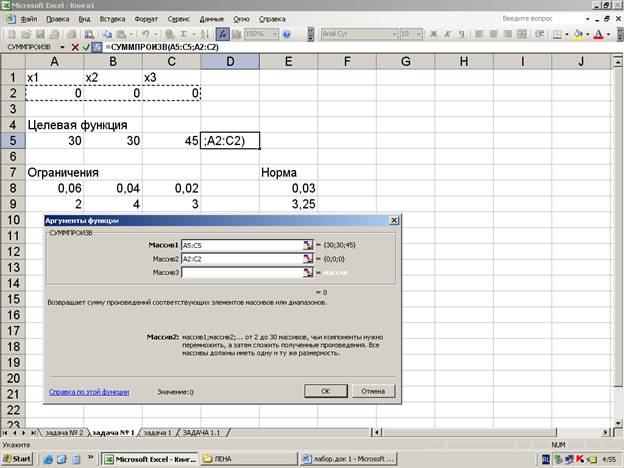
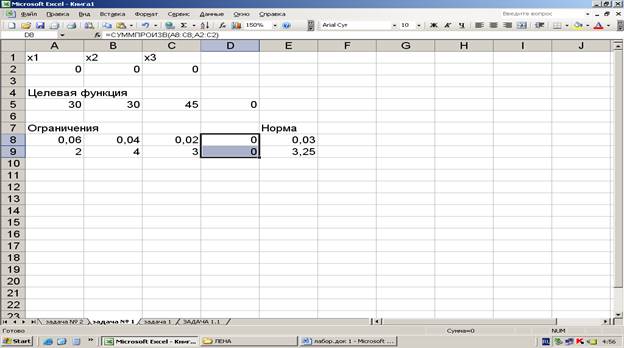
3 Вводим зависимость для ограничений

4. запускаем команду поиск решений

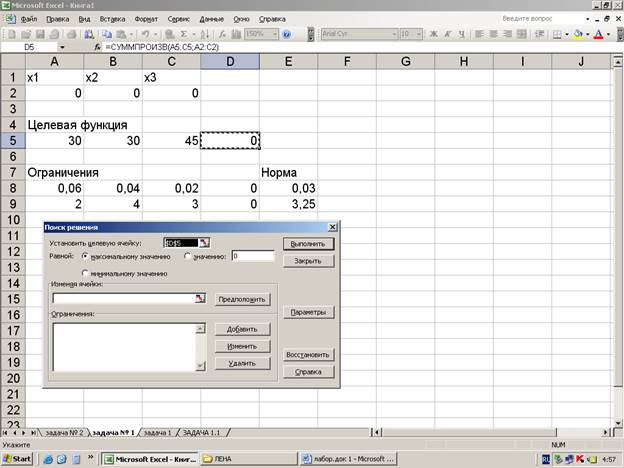
4.1 Вводим изменение ячеек

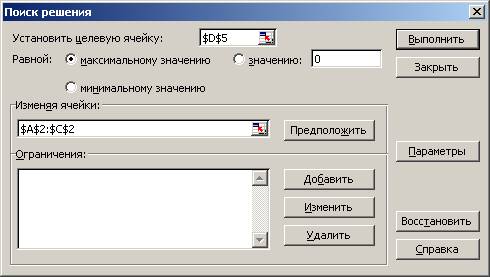
4.2 Вводим ограничения

1)

2)

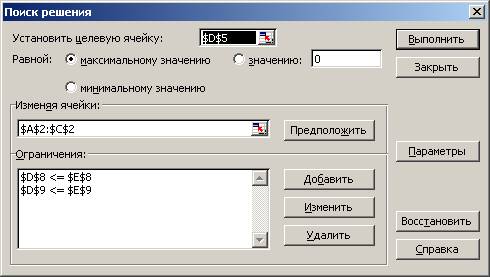
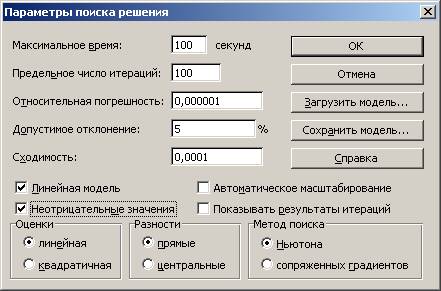
4.3. Вводим параметры для решения задачи

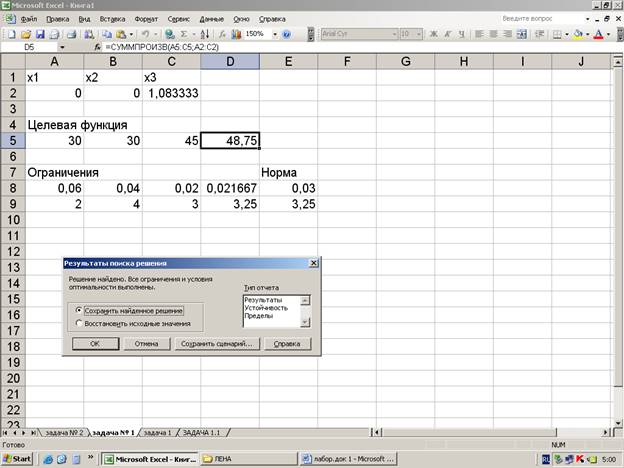
5. Результат поиска решений

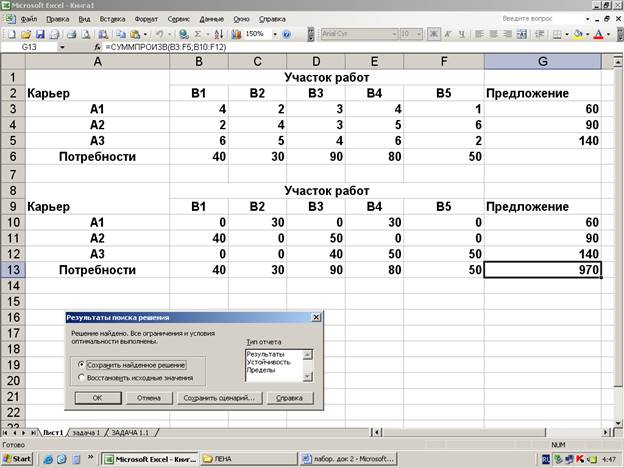
Задача № 2

Компания, занимающаяся ремонтом автомобильных дорог, в следующем месяце будет проводить ремонтные работы на пяти участках дорог. Песок на участки ремонтных работ может доставляться из трех карьеров, месячные объекты предложений по карьерам известны. Из планов производства ремонтных работ известны месячные объемы потребностей по участкам работ. Имеются экономические оценки транспортных затрат

(в у.е.) на перевозку 1 тонны песку с карьеров на ремонтные участки.

Карьер	Участок работ	Предложение
В1	В2	В3	В4	В5
А1	4	2	3	4	1	60
А2	2	4	3	5	6	90
А3	6	5	4	6	2	140
Потребности	40	30	90	80	50

Требуется:

1. Предложить план перевозок песка на участки ремонта автодорог, который обеспечивает минимальные совокупные транспортные издержки.
2. Определить, что произойдет с оптимальным планом, если изменятся условия перевозок: а) появится запрет на перевозки от первого карьера до второго участни работ; б) по этой коммуникации будет ограничен объем перевозок 3 тоннами  

Решение

1. Экономико-математическая модель задачи

f(x) = 5x₁₁ + 3x₁₂ + 4x₁₃ + 6x₁₄ + 4x₁₅ + 3x₂₁ + 4x₂₂ + 10x₂₃ + 5x₂₄ + 7x₂₅ + 4x₃₁ + 6x₃₂ + 9x₃₃ + 3x₃₄ + 4x₃₅ → min

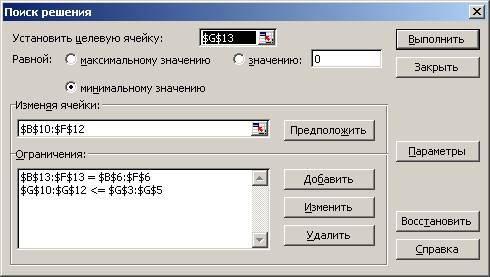
Функциональные ограничения

  - по карьерам

5x₁₁₊3x₁₂ + 4x₁₃ + 6x₁₄ + 4x₁₅≤ 60

3x₂₁ + 4x₂₂ + 10x₂₃ + 5x₂₄ + 7x₂₅ ≤ 90

4x₃₁ + 6x₃₂ + 9x₃₃ + 3x₃₄ + 4x₃₅ ≤ 140

  - по участкам работ

5x₁₁₊ 3x_{21 +} 4x₃₁ = 40

3x₁₂₊  4x₂₂₊ 6x₃₂ = 30

4x₁₃ + 10x₂₃ + 9x₃₃ = 90

6x₁₄ + 5x₂₄ + 3x₃₄ = 80

4x₁₅ + 7x₂₅ + 4x₃₅ = 50

1 Ввести исходные данные

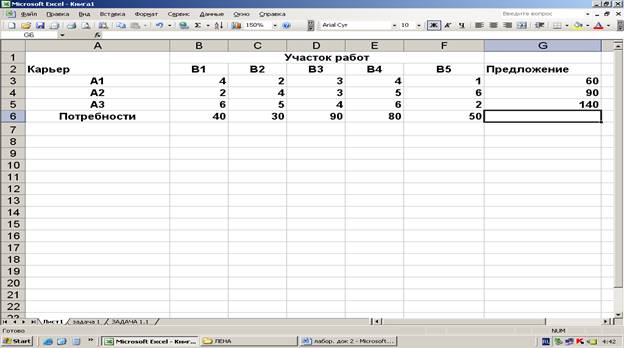
2 Ввести зависимости для ограничений и для целевой функции

                

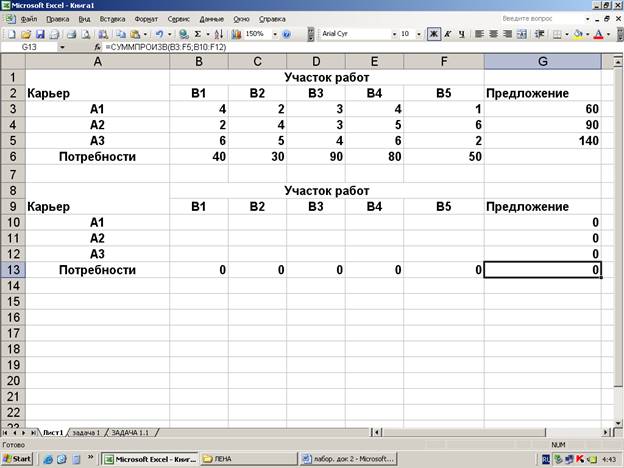
4. Запустить команду поиск решений

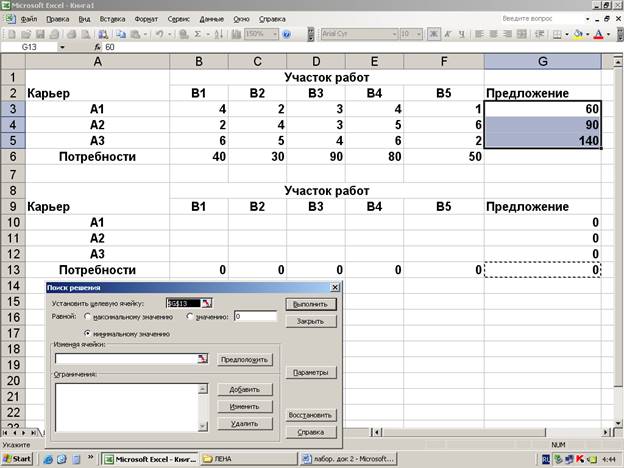
4.1 Ввести изменение ячеек

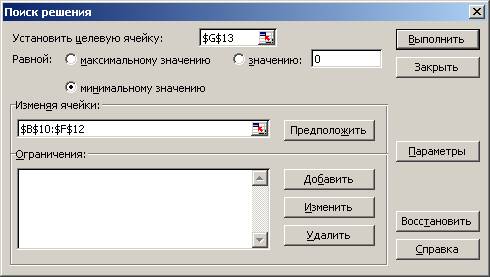
4.2 Ввести ограничение

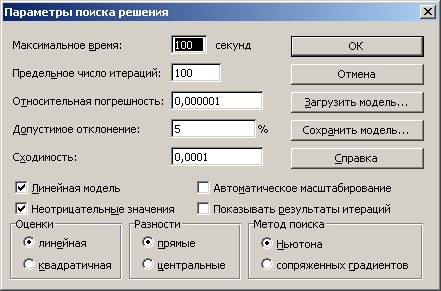
4.3 Ввести параметры поиска решений

4.4 Результат поиска решений