Содержание
Задача 1. 3
Задача 2. 5
Задача 3. 6
Задача 4. 9
Задача 5. 11
Задача 6. 13
Список использованной
литературы.. 14
Задача 1.
Определите
среднее число работников в базисном и отчетном году:
|
Группы предприятий по числу работников на 1
предприятии, чел
|
Число предприятий в базисном году, %
|
Всего работает в отчетном году, чел
|
До 30
|
23,7
|
150
|
|
30 – 50
|
45,9
|
540
|
|
50 – 150
|
30,4
|
350
|
Решение
Определим
средние по группам предприятий
|
Группы предприятий по числу работников на 1
предприятии, чел
|
Число предприятий в базисном году, %
|
Всего работает в отчетном году, чел
|
|
15
|
23,7
|
150
|
|
80
|
45,9
|
540
|
|
100
|
30,4
|
350
|
Для
определения среднего числа работников в базисном году, применяется средняя
арифметическая взвешенная:
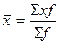 ,
,
где х
– число работников
f – доля предприятий
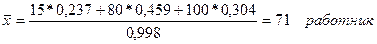
Для
расчета средней численности применяется формула средней гармонической
взвешенной:
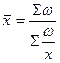 ,
,
где
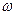 - численность
работающих по группе
- численность
работающих по группе
х – численность одного
предприятия
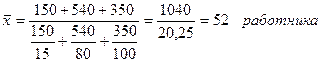
Задача 2.
Согласно
данным обследования производственной деятельности ткачих двух бригад, среднее
квадратическое отклонение дневной выработки тканей составляет для всей
совокупности ткачих 20 м, для ткачих первой бригады – 15 м, второй бригады – 10
м. Определите межгрупповую дисперсию дневной выработки тканей, если известно,
что численность ткачих в первой бригаде – 40 человек, во второй – 60 человек.
Решение
Межгрупповая дисперсия:
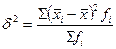 .
.
где 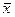 - общая средняя арифметическая для всей изучаемой
совокупности
- общая средняя арифметическая для всей изучаемой
совокупности
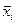 - средняя по отдельной
группе
- средняя по отдельной
группе
Определим общую среднюю арифметическую для
всей изучаемой совокупности по формуле средней арифметической взвешенной:
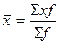 ,
,
где х – дневная выработка
f – Численность ткачей.
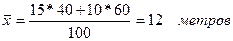
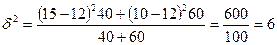
Задача 3.
Для
изучения качества продукции при выборочном бесповторном отборе получены
следующие данные о недовесе выпеченных батонов:
|
Недовес 1 батона, грамм
|
Число обследованных батонов
|
|
40 - 60
|
9
|
|
60 - 80
|
20
|
|
80 - 100
|
34
|
|
100 - 120
|
22
|
|
120 - 140
|
8
|
Определите:
1) коэффициент вариации; 2) с вероятностью 0,997 пределы, в которых можно
ожидать средний недовес всей партии батонов, состоящей из 600 батонов; 3) с
вероятностью 0,954 пределы, в которых можно ожидать долю батонов с недовесом
более 100 грамм.
Решение
1.
определим коэффициент вариации.
|
Недовес 1 батона, грамм
|
Число обследованных
батонов
|
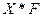
|
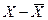
|
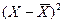
|
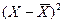 F F
|
|
50
|
9
|
450
|
-40
|
1600
|
14400
|
|
70
|
20
|
1400
|
-20
|
400
|
8000
|
|
90
|
34
|
3060
|
0
|
0
|
0
|
|
110
|
22
|
2420
|
20
|
400
|
8800
|
|
130
|
8
|
1040
|
40
|
1600
|
12800
|
|
93
|
8370
|
|
|
44000
|
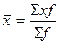
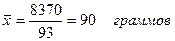
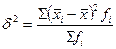
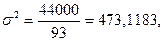
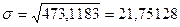
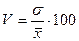
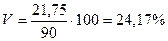
Так как 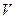 =24%, то данная совокупность однородна
=24%, то данная совокупность однородна
2
определим с вероятностью 0,997 пределы, в которых можно ожидать средний недовес
всей партии батонов, состоящей из 600 батонов;
Границы
генеральной средней определяются как:
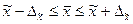 ,
,
где
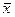 - генеральная средняя,
- генеральная средняя,
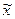 - выборочная средняя,
- выборочная средняя,
Δ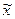 - предельная ошибка выборочной средней:
- предельная ошибка выборочной средней:
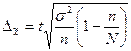 ,
,
где 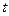 - коэффициент доверия,
- коэффициент доверия,
N – объем генеральной совокупности,
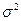 - дисперсия признака выборочной совокупности.
- дисперсия признака выборочной совокупности.
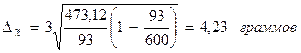
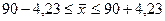
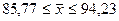
С
вероятностью 0,997 можно ожидать недовес в пределах от 85,77 до 94,23 граммов.
3
определим с вероятностью 0,954 пределы, в которых можно ожидать долю батонов с
недовесом более 100 грамм
Границы
генеральной доли находятся как
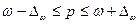 ,
,
где р
– генеральная доля,
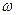 - выборочная доля:
- выборочная доля:
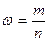
где 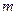 - число единиц,
обладающих данным признаком,
- число единиц,
обладающих данным признаком,
n - объем выборочной совокупности.
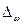 - предельная ошибка доли:
- предельная ошибка доли:
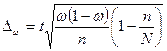 .
.
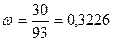
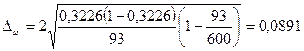
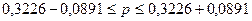
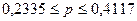
С
вероятностью 0,954 можно ожидать долю батонов с недовесом более 100 грамм в
пределах от 23,35% до 41,17%
Задача 4.
Имеются
данные о производстве однотипной продукции:
|
Предприятие
|
Затраты на производство
продукции, тыс. руб
|
Изменение стоимости
единицы изделия в отчетном периоде по сравнению с базисным, %
|
|
квартал
|
|
I
|
II
|
|
1
|
432,9
|
2 346,9
|
-7,3
|
|
2
|
452,4
|
4 562,9
|
Без изменения
|
Определите:
общие индексы себестоимости, затрат на производство, объема производства.
Сделайте
выводы.
Решение
Общий
индекс себестоимости:
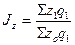 ,
,
где
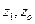 - себестоимость в
отчетном и базисном периоде соответственно,
- себестоимость в
отчетном и базисном периоде соответственно,
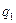 - физический объем производства в отчетном периоде
- физический объем производства в отчетном периоде
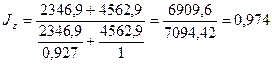
Себестоимость
в отчетном квартале по сравнению с базисным снизилась на 2,6%.
Общий
индекс затрат на производство:
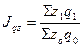
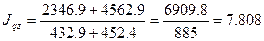
Затраты
на производство в отчетном квартале по сравнению с базисным увеличились в 7,808
раз.
Общий
индекс объема производства:
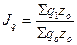 .
.
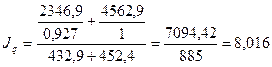
Объем
производства в текущем квартале по сравнению с базисным увеличился в 8,016 раз.
Задача 5.
Имеются
следующие данные об урожайности и валовом сборе пшеницы:
Культуры
|
Урожайность, ц⁄га
|
Валовой сбор, млн ц
|
|
Период
|
Период
|
|
базисный
|
отчетный
|
базисный
|
отчетный
|
|
Пшеница озимая
Пшеница яровая
|
16,9
10,3
|
17,9
11,0
|
138
163
|
167
182
|
Рассчитайте
индексы урожайности переменного, фиксированного состава, индекс структурных
сдвигов. Сделайте выводы.
Решение
Схема
индекса переменного состава:
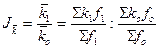 ,
,
где
k –
изучаемый показатель в отчетном и базисном периоде соответственно.
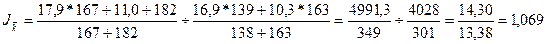
Урожайность
увеличилась на 6,9%.
Индекса
постоянного состава, схема которого:
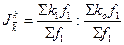 .
.
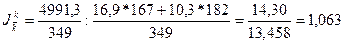
За
счет изменения урожайности по каждому виду культур в среднем урожайность
увеличилась на 6,3%.
Индекс структурных сдвигов, схема которого:
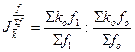 .
.
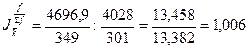
Урожайность
увеличилась за счет структурных сдвигов на 0,6%
Задача 6.
По
приведенным данным о базисных темпах прироста населения (%) одного из регионов
России, рассчитайте цепные темпы роста и прироста, а также среднегодовой темп
прироста за период с 1994 по 2002 годы:
|
1994
|
1995
|
1996
|
1997
|
1998
|
1999
|
2000
|
2001
|
2002
|
|
0,0
|
5,1
|
7,2
|
8,1
|
8,9
|
9,8
|
10,2
|
10,2
|
10,1
|
Решение
Год
|
Базисные
|
Цепные
|
|
Темп прироста
|
Темп роста
|
Темп прироста
|
Темп роста
|
|
1994
|
0,0
|
100
|
|
|
|
1995
|
5,1
|
105,1
|
+5,1
|
105,1
|
|
1996
|
7,2
|
107,2
|
+1,9
|
101,9
|
|
1997
|
8,1
|
108,1
|
+0,8
|
100,8
|
|
1998
|
8,9
|
108,9
|
+0,7
|
100,7
|
|
1999
|
9,8
|
109,8
|
+0,8
|
100,8
|
|
2000
|
10,2
|
110,2
|
+0,3
|
100,3
|
|
2001
|
10,2
|
110,2
|
0
|
100
|
|
2002
|
10,1
|
110,1
|
-0,1
|
99,9
|
Темп роста = X1 / X0 *100%
Темп прироста = 100 – Темп роста
-
средний темп роста:
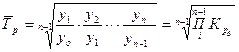
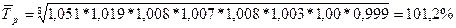
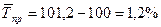
Список использованной литературы
1.
Елисеева И.И. Юзбашев М.М. Общая теория статистики:
Учебник.- М.: Финансы и статистика, 1995.-368 с.
2.
Громыко Г.Л. Общая теория статистики: Практикум. – М.:
Инфра – М, 1999. – 139 с.
3.
Ефимова М.Р., Ганченко О.И., Петрова Е.В. Практикум по
общей теории статистики: Учеб.пособие. – М.: Финансы и статистика, 1999. – 280
с.
4.
Общая теория статистики. Статистическая методология в
изучении коммерческой деятельности: Учебник ∕ А.И.Харламов, О.Э.Башина,
В.Т.Бабурин и др.- М.: Финансы и статистика, 1994. – 269 с.
5.
Практикум по теории статистики./Под ред.
Н.Н,Ряузова – М.: Финансы и статистика,
1981. – 278 с.
6.
Ряузов Н.Н. Общая
теория статистики.– М.: Статистика,1984.–343 с.
7.
Теория статистики: Учебник ∕ Под ред. Р.А.
Шмойловой. – М.: Финансы и статистика, 1996. – 464 с.