Вариант № 1

Данные, характеризующие прибыль торговой компании «Все для себя» за первые  10 месяцев 2004 года (в тыс. руб.), даны в следующей таблице:

январь	февраль	март	апрель	май	июнь	июль	август	сентябрь	октябрь
382+N	402+N	432+N	396+N	454+N	419+N	460+N	447+N	464+N	498+N

N=9 - последняя цифра номера зачетной книжки.

В контрольной работе с использованием табличного процессора Ехсеl необходимо выполнить следующие вычисления и построения:

1. Построить диаграмму рассеяния.

2. Убедится в наличии тенденции (тренда) в заданных значениях прибыли фирмы и возможности принятия гипотезы о линейном тренде.

3. Построить линейную парную регрессию (регрессию вида 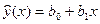). Вычисление коэффициентов  b₀, b₁  выполнить методом наименьших квадратов.

4. Нанести график регрессии на диаграмму рассеяния.

5. Вычислить значения статистики F и коэффициента детерминации R². Проверить гипотезу о значимости построенного уравнения регрессии.

6. Вычислить выборочный коэффициент корреляции и проверить гипотезу о ненулевом его значении.

7. Вычислить оценку дисперсии случайной составляющей эконометрической модели.

8. Проверить гипотезы о значимости вычисленных коэффициентов b₀, b₁  .

9. Построить доверительные интервалы для коэффициентов b₀, b₁.

10. Построить доверительные интервалы для дисперсии случайной составляющей эконометрической модели.

11. Построить доверительную область для условного математического ожидания М(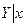)( по оси Х откладывать месяцы январь - декабрь). Нанести границы этой области на диаграмму рассеяния.

12. С помощью линейной парной регрессии сделать прогноз величины прибыли на ноябрь и декабрь месяц и нанести эти значения на диаграмму рассеяния. Сопоставить эти значения с границами доверительной области для условного математического ожидания М(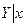) и сделать вывод о точности прогнозирования с помощью построенной регрессионной модели.

Решение.

1.                При N=9 данные, характеризующие прибыль торговой компании «Все для себя» за первые  10 месяцев,  задаются следующей таблицей:

№ месяца	Месяц ( x)	Прибыль (y)
1	январь	391
2	февраль	441
3	март	405
4	апрель	463
5	май	428
6	июнь	469
7	июль	456
8	август	456
9	сентябрь	473
10	октябрь	507

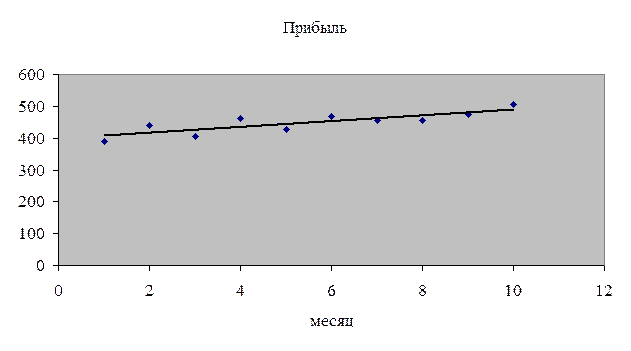
Используя исходные данные, строим диаграмму рассеяния:

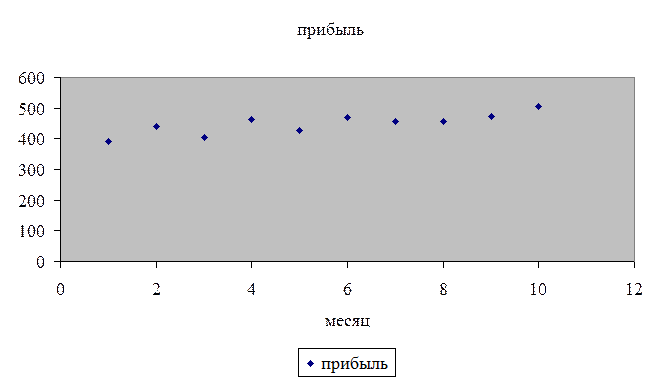
2.                На основе анализа диаграммы рассеяния убеждаемся в наличии тенденции  увеличения прибыли фирмы  и выдвигаем гипотезу о линейном тренде.

3. Полагаем, что связь между факторами Х и У может быть описана линейной функцией 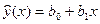. Решение задачи нахождения коэффициентов  b₀, b₁  основывается на применении метода наименьших квадратов и сводится к решению системы двух линейных уравнений с двумя неизвестными b₀, b₁ :

 b₀ n + b₁ Σx_i = Σy_i,

 b₀ Σx_i +  b₁ Σx_i² = Σx_iy_i.

Составляем вспомогательную таблицу:

№	х	y	x2	ху	y2
1	1	391	1	391	152881
2	2	441	4	882	194481
3	3	405	9	1215	164025
4	4	463	16	1852	214369
5	5	428	25	2140	183184
6	6	469	36	2814	219961
7	7	456	49	3192	207936
8	8	456	64	3648	207936
9	9	473	81	4257	223729
10	10	507	100	5070	257049
сумма	55	4489	385	25461	2025551

Для нашей задачи система имеет вид:

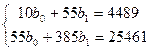
Решение этой системы можно получить по правилу Крамера:

      Σy_i×Σx_i² – Σx_iy_i×Σx_i                nΣx_iy_i – Σx_iΣy_i           

b₀ = —————————,     b₁ = ——————— .

          nΣx_i² – (Σx_i)²                          nΣx_i² – (Σx_i)²    

Получаем:, .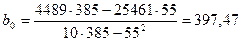

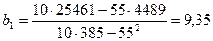Таким образом, искомое уравнение регрессии имеет вид:     y =397,47 + 9,35x.

4.     Нанесем график регрессии на диаграмму рассеяния.

5.                Вычислим значения статистики F и коэффициента детерминации R². Коэффициент детерминации  рассчитаем по формуле   R² = r_xy² = 0,831²  = 0,691. Проверим адекватность модели (уравнения регрессии) в целом с помощью F-критерия.  Рассчитаем значение статистики F  через коэффициент детерминации R² по формуле:

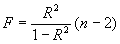
Получаем: 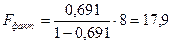. Зададим уровень значимости α =0,05, по таблице находим квантиль распределения Фишера F_0,01;1;8 = 5,32, где 1 – число степеней свободы.

F_факт. > F_0,01;1;8, т.к. 17,9 > 5,32.

Следовательно,  делаем вывод о значимости уравнения регрессии при 95% - м уровне значимости.

6.                Вычислим выборочный коэффициент корреляции и проверим гипотезу о ненулевом его значении.

Рассчитаем  выборочный коэффициент корреляции по формуле:    

nΣx_iy_i – Σx_iΣy_i

r_xy =—————¾­ ¾¾——¾— ,

√nΣx_i² – (Σx_i)² √nΣу_i² – (Σу_i)²

Получаем:

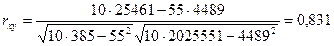
Проверка существенности отличия коэффициента корреляции от нуля проводится по схеме:                                                                                                

если 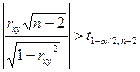     , то гипотеза о существенном отличии коэффициента корреляции от нуля принимается, в противном случае отвергается.

Здесь t_1-α/2,n-2 – квантиль распределения Стьюдента, α -  уровень значимости или уровень доверия, n – число наблюдений, (n-2) – число степеней свободы. Значение α задается. Примем α = 0,05, тогда t_1-α/2,n-2 = t_0,975,8 = 2,37.  Получаем: .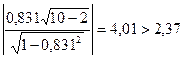

Следовательно, коэффициент корреляции существенно отличается от нуля и существует сильная линейная связь между х и у.

С использованием табличного процессора Ехсеl проведем регрессионную статистику:

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,831346
R-квадрат	0,691135
Нормированный R-квадрат	0,652527
Стандартная ошибка	20,0755
Наблюдения	10
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	1	7214,694	7214,694	17,90132	0,002872
Остаток	8	3224,206	403,0258
Итого	9	10438,9
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%
Y-пересечение  (b0)	397,4667	13,71418	28,98217	2,17E-09	365,8417
Переменная X 1 (b1)	9,351515	2,21024	4,230995	0,002872	4,254689

Вычисленные значения коэффициентов  b₀, b₁,  значения статистики F, коэффициента детерминации R² выборочного коэффициента корреляции r_xy совпадают с выделенными в таблице.

7. Оценка дисперсии случайной составляющей эконометрической модели вычисляется по формуле .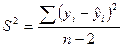

Используя результаты регрессионной статистики, получаем .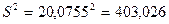

8. Проверим значимость вычисленных коэффициентов b₀, b₁  по t-критерию Стьюдента.

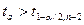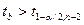Для этого проверяем выполнение неравенств:  и , где

,

,    .

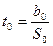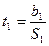
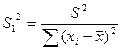Используем результаты регрессионной статистики:

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	397,4667	13,71418	28,98217	2,17E-09	365,8417	429,0916
Переменная X 1	9,351515	2,21024	4,230995	0,002872	4,254689	14,44834

Получаем: ; .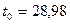

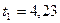Примем α = 0,05, тогда  t_1-α/2,n-2 = t_0,975,8 = 2,37.

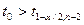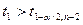Так как  и , делаем вывод о значимости коэффициентов линейного уравнения регрессии.

9. Доверительные интервалы для коэффициентов b₀, b₁ получаем с помощью результатов регрессионной статистики.

Доверительный интервал для коэффициента  b₀  уравнения регрессии:

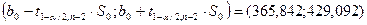
Доверительный интервал для коэффициента b₁ уравнения регрессии:

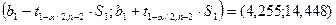
10. Построим доверительный интервал для дисперсии случайной составляющей эконометрической модели по формуле:

.

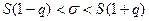Примем α = 0,05, тогда по таблице для 10-элементной выборки q = 0,65. Получаем:

.

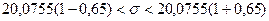
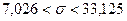11. Построим доверительную область для условного математического ожидания М().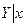

Доверительные интервалы для уравнения линейной регрессии : 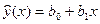    находятся по формуле:

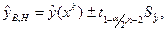
где 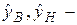 соответственно верхняя и нижняя границы доверительного интервала; 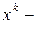значение независимой переменной  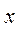для которого определяется доверительный интервал, 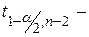квантиль распределения Стьюдента, 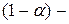доверительная вероятность, (n-2) – число степеней свободы;

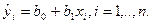
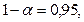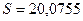Рассмотрим уравнение :     y =397,47 + 9,35x.  Пусть  тогда . Зная  и 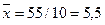, заполним таблицу:

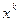
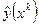
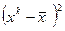
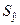
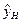
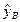
1	406,8182	20,25	4,280	398,857	414,779
2	416,1697	12,25	4,817	407,210	425,130
3	425,5212	6,25	5,300	415,663	435,379
4	434,8727	2,25	5,742	424,192	445,554
5	444,2242	0,25	6,153	432,780	455,669
6	453,5758	0,25	6,538	441,415	465,736
7	462,9273	2,25	6,901	450,091	475,764
8	472,2788	6,25	7,247	458,800	485,758
9	481,6303	12,25	7,576	467,538	495,722
10	490,9818	20,25	7,892	476,302	505,661
сумма	82,5
11	500,3333	30,25	8,196	485,089	515,578
12	509,6848	42,25	8,489	493,896	525,474

График уравнения регрессии, доверительная полоса, диаграмма рассеяния:

12. С помощью линейной парной регрессии сделаем прогноз величины прибыли на ноябрь и декабрь месяц:

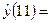500,3333.

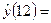509,6848.

 Нанесем эти значения на диаграмму рассеяния.

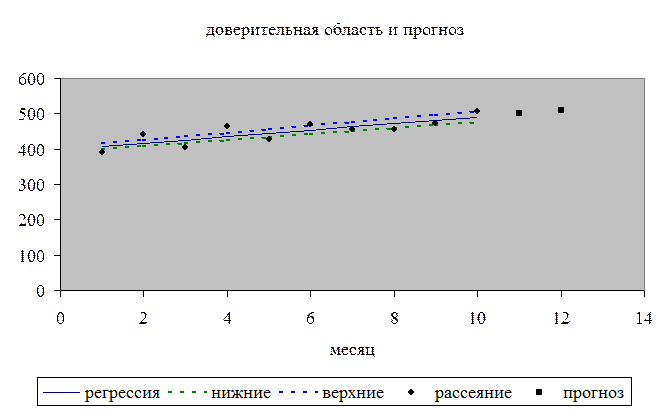
Эти значения сопоставимы с границами доверительной области для условного математического ожидания М().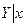

Точность прогнозирования: с вероятностью 0,95 прибыль в ноябре находится в интервале (485,089; 515,578); прибыль в декабре находится в интервале (493,896; 525,474).