СОДЕРЖАНИЕ
ВВЕДЕНИЕ. 3
1.
статистическоЕ ИЗУЧЕНИЕ РЕЗУЛЬТАТОВ ДЕЯТЕЛЬНОСТИ ОРГАНИЗАЦИИ МЕТОДОМ
ГРУППИРОВОК (НА ПРИМЕРЕ ДЕЯТЕЛЬНОСТИ КОММЕРЧЕСКИХ БАНКОВ) 4
1.1. Система показателей кредитной деятельности
банков. 4
1.2. Понятие статистические сводки и группировки. 6
1.3. Группировка. Понятие и применение. 8
1.4. Выбор
группировочных признаков. 9
1.5. Техника выполнения группировок. 11
2.
Расчетная часть. 14
3.
АНАЛИТИЧЕСКАЯ ЧАСТЬ. 33
3.1. Постановка задачи. 33
3.2. Методика решения задачи. 33
3.3. Технология выполнения компьютерных расчетов. 34
3.4. Анализ результатов статистических
компьютерных расчетов. 37
ЗАКЛЮЧЕНИЕ. 38
СПИСОК
ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ.. 40
ВВЕДЕНИЕ
Мониторинг эффективности
функционирования банковской системы является одной из наиболее важных задач в
государственной политике Российской Федерации в кредитной сфере. Анализ влияния
реформ на состояние банковской системы, отслеживание динамики эффективности
деятельности банков, снижение системного риска являются основными задачами
государственных аналитических институтов и требуют применения статистических
методов анализа. Исследованию результатов банковской деятельности посвящено
значительное количество научных и прикладных исследований, но показателю
эффективности работы банков и банковской системы в целом уделено недостаточно
внимания. Современные статистические методики оценивания эффективности
деятельности банков обязательно должны включаться в инструментарий банковского
аналитика, однако их адаптация к анализу банковской системы Российской
Федерации является недостаточно разработанной областью.
Таким образом,
исследование результатов деятельности коммерческих банков является чрезвычайно
актуальной задачей статистического исследования организации финансово-кредитной
сферы.
Целью курсовой работы
является изучение системы показателей, характеризующих результаты деятельности
банков, а также особенности применения метода группировок для изучения данных
показателей.
Задачей курсовой работы
является изучение результатов деятельности организации методом группировок на
основе деятельности коммерческих банков. Рассмотрение системы показателей,
характеризующих деятельность банков, структуры и качества активов, а также
доходов и рентабельности кредитной деятельности. Группировка банков по величине
пассивов. Построение гистограммы отображающее графическое построение моды и
медианы. Расчет таких показателей как средней взвешенной, среднего
квадратического отклонения, коэффициента вариации, арифметической средней.
Установить характер связи между величиной пассивов и работающих активов,
измерить тесноту корреляционной связи между признаками с использованием
коэффициента детерминации и эмпирического отношения. Определить ошибку выборки
средней величины пассивов банков и границы в которых будет находиться средняя
величина пассивов в генеральной совокупности.
Определить динамику
остатков средств физических лиц на счетах банка на 1 января. Определить остаток
средств на всех счетах. Произвести факторный анализ динамики остатков средств в
национальной валюте на валютных счетах, рассчитав абсолютный прирост остатков средств
на 1 января 2004 г.
по сравнению с 1 января 2003
г. за счет изменения: курса доллара, остатков средств на
счетах.
По исходным данным о
банках, представленным в таблице 12, произвести группировку 20 банков по
величине кредитных вложений. Подобрать 3-4 наиболее экономически связанных и
существенных показателя, определить их суммарные величины по каждой группе, а
также вычислить показатели в относительном выражении. Результаты группировки
изложить в сводной групповой таблице.
Для группировки банков с
помощью аналитической группировки проанализировать зависимость величины
кредитных вложений от других экономических показателей, характеризующих
деятельность банков.
1.
статистическоЕ ИЗУЧЕНИЕ РЕЗУЛЬТАТОВ ДЕЯТЕЛЬНОСТИ ОРГАНИЗАЦИИ МЕТОДОМ
ГРУППИРОВОК (НА ПРИМЕРЕ ДЕЯТЕЛЬНОСТИ КОММЕРЧЕСКИХ БАНКОВ)
1.1. Система показателей кредитной деятельности банков
Результатом деятельности банка
считаются объемы обслуженных депозитов и кредитов, а в качестве издержек
выступают все операционные расходы, включая процентные выплаты.
При подходе с ориентацией на прибыль
в качестве единственной цели рассматривается полученная прибыль, а все входы и
выходы банковской деятельности как используемые для ее получения ресурсы. Такой
подход позволяет совместно рассматривать эффективность использования входных
ресурсов и эффективность выпуска, что уменьшает вероятность неправильной
спецификации модели деятельности банка.
Разновидностью данного подхода
является подход с ориентацией на издержки, при котором в качестве цели
выступает минимизация совокупных издержек банка.
При подходе с ориентацией на
управление риском банк рассматривается как организация, которая принимает на
себя различные виды рисков с целью получения дохода. В этом случае в качестве
входов рассматриваются рисковые характеристики процесса банковской
деятельности, а в качестве выхода - банковская прибыль или рыночная стоимость
акций банка.
Следует отметить, что статистическая
оценка эффективности деятельности банка может сильно варьировать в зависимости
от выбранного подхода.
Статистический анализ эффективности
позволяет провести сравнение различных направлений деятельности банка, выбор
приоритетных и исключение неэффективных направлений. Отдельной задачей является
оценка эффективности деятельности филиалов банка. Данная оценка позволяет
менеджерам оценить состояние отдельных филиалов и определить необходимые
преобразования для увеличения эффективности их работы.
Информация об эффективности
деятельности отдельных банков и всей отрасли в целом может помочь
государственным органам анализировать состояние системы, динамику ее развития и
решения других основных задач. Во-первых, информация о динамике эффективности
очень полезна при анализе результатов реформ банковского сектора и других
глобальных изменений. В мировой практике многие статистические исследования
эффективности банковского сектора направлены на исследование динамики
эффективности в период значительных изменений банковской системы.
Современная статистическая методика
оценки эффективности деятельности банков является еще одним инструментом
анализа, необходимым исследователям в их проектах. В силу значительной
взаимосвязи показателя эффективности работы банка со многими другими
(надежность банка, уровень развития его организационной структуры, степень
зависимости от других рыночных агентов) анализ эффективности может быть
использован в качестве основного или дополнительного инструмента исследований.
Клиенты банковской системы могут
использовать информацию об эффективности деятельности банка и ее динамике при
выборе своего банковского партнера. С этой точки зрения оценки эффективности
являются аналогом рейтингов банка, присвоенных ему международными и российскими
рейтинговыми агентствами. Таким образом, при рассмотрении показателя
эффективности банковской деятельности с разных позиций проявляется его
многоаспектный характер, что позволяет сделать вывод о сложности его внутренней
структуры. Вследствие этого возникает необходимость исследования составных
частей данного показателя и определения основных его компонентов.
В качестве характеристик
макроэкономического окружения могут использоваться следующие:
- динамика валового внутреннего
продукта страны;
- динамика инвестиций в реальный
сектор экономики;
- уровень безработицы;
- уровень инфляции;
- процентная ставка долгосрочных
государственных ценных бумаг;
- процентная ставка рефинансирования.
Большинство данных показателей
приобретают значимость лишь при совместном сравнительном исследовании
банковских систем различных стран.
К числу факторов, специфичных для
банка, относят размер банка, набор предоставляемых им услуг, форму
собственности банка и его филиальную структуру. Взаимосвязь размера банка и
набора предоставляемых им услуг с эффективностью его работы была подробно
рассмотрена при выделении основных компонентов эффективности.
1.2. Понятие статистические сводки и группировки.
В результате первой стадии
статистического исследования (статистического наблюдения) деятельности банков получают
статистическую информацию, представляющую собой большое количество первичных,
разрозненных сведений об отдельных единицах банковской деятельности
исследования (например, информация о величине активов и пассивов, величине
процентных доходов или расходов и др.)
Дальнейшая задача статистики
заключается в систематизации этих материалов в определенном порядке и сводной
характеристики всей совокупности фактов при помощи обобщающих показателей,
отражающих сущность социально-экономических явлений и определенные
статистические закономерности.
Сводка - особая стадия статистического
исследования, в ходе которой систематизируются первичные материалы
статистического наблюдения.
Проведение сводки включает 3 этапа:
1. предварительный контроль материалов
(проверка исходных данных);
2. группировка данных по заданным
признакам, определение производных показателей;
3. оформление результатов сводки в виде
статистических таблиц.
Предварительный контроль включает
логическую проверку данных, т.е. смысловую согласованность сведений, исключение
"нелогичных" данных и арифметическую согласованность.
Группировка данных производится в
соответствии с программой сводки для того, чтобы впоследствии представить
полученную информацию в виде, доступном для восприятия.
Результаты группировки оформляются в
виде группировочных таблиц, делающих информацию обозримой.
Таблица содержит сводную числовую
характеристику исследуемой совокупности по одному или нескольким существенным
признакам, взаимосвязанным логикой анализа.
Статистическая сводка - это научно организованная обработка
материалов наблюдения, включающая в себя систематизацию, группировку данных,
составление таблиц, подсчет групповых и общих итогов, расчет производных
показателей (средних, относительных величин). Она позволяет перейти к
обобщающим показателям совокупности в целом и отдельных ее частей, осуществлять
анализ и прогнозирование изучаемых процессов.
Статистическая сводка должна проводится по
определенной программе и плану.
Программа статистической сводки
устанавливает следующие этапы:
·
выбор
группировочных признаков; определение порядка формирования групп;
·
разработка
системы статистических показателей для характеристики групп и объекта в целом;
·
разработка
макетов статистических таблиц для представления результатов сводки.
План статистической сводки содержит
указания о последовательности и сроках выполнения отдельных частей сводки, ее
исполнителях и порядке изложения и представления результатов.
В сводке статистического материала
отдельные единицы совокупности статистической совокупности объединяются в
группы при помощи метода группировок.
1.3. Группировка. Понятие и применение
Статистическая группировка -
объединение единиц совокупности в некоторые группы, имеющие свои характерные
особенности, общие черты и сходные размеры изучаемого признака.
Метод группировок является основой
применения других методов статистического анализа основных сторон и характерных
особенностей изучаемых явлений. По своей роли в процессе исследования метод
группировок выполняет некоторые функции, аналогичные функциям эксперимента в
естественных науках: посредством группировки по отдельным признакам и
комбинации самих признаков статистика имеет возможность выявить закономерности
и взаимосвязи явлений в условиях, в известной мере ею определяемых. При
использовании метода группировок появляется возможность проследить
взаимоотношение различных факторов и определить силу их влияния на
результативные показатели.
Изучая количественную сторону
массовых общественных явлений в неразрывной связи с их качественными
особенностями, статистика стремится показать совокупность явлений в
дифференциации, в многообразии их типов, рассмотреть взаимосвязи и соотношения
между последними. С помощью метода группировок решаются сложные задачи
статистического анализа. Учитывая, что необходимость группировки
обусловливается, прежде всего, наличием качественных различий между изучаемыми
явлениями, первую задачу группировок можно сформулировать как задачу выделения
в составе массового явления тех его частей, которые однородны по качеству и
условиям развития, в которых действуют одни и те же закономерности влияния
факторов. В результате такой группировки выделяются социально-экономические
типы (а отсюда и название группировки - типологическая) как выражение
конкретного общественного процесса, его форм и разветвлений, как выражение
существенных черт, общих для множества единичных явлений.
1.4. Выбор группировочных
признаков
Выбор группировочных признаков
всегда должен быть основан на анализе качественной природы исследуемого
явления. Всесторонний теоретико-экономический анализ сущности и закономерностей
развития явления должен быть направлен на то, чтобы в соответствии с целью и
задачами исследования положить в основание группировки существенные признаки. В
зависимости от конкретных условий группировочные признаки должны
видоизменяться, т.е. должны быть специализированы при выделении одного и того
же типа в различных условиях. Так, в настоящее время в промышленности при
группировке банков по размерам капитала могут использоваться показатели собственного
капитала, величине привлеченного капитала в разбивке по источнику привлечения
(физические лица / юридические лица). Если для капиталоемких отраслей (банковской
деятельности) в качестве группировочного признака целесообразно использовать величину
капитала, то для фондоемких отраслей - стоимость промышленно-производственных
фондов; для энергоемких отраслей - количество потребленной электроэнергии.
Вместе с тем следует учитывать, что полную
характеристику каждому типу явлений можно дать при использовании системы
признаков (системы показателей). Только совокупность признаков позволяет
отобразить процессы развития, всесторонне выявить реальные связи,
взаимоотношения отдельных сторон процесса.
Использование одного признака,
характеризующего лишь одну сторону, одну черту в развитии явления, может
привести к искажению действительности, поскольку в последней, как правило,
переплетаются различные, подчас противоположные тенденции и направления.
Множественность признаков, характеризующих объекты, является следствием их
многосторонности и многообразия реальных связей между объектами.
В зависимости от вида группировочных
признаков различают группировки по количественным и качественным признакам.
Качественный признак отражает
определенные свойства, качества данного явления и записывается в виде текста.
Если качественный признак имеет мало разновидностей, то количество групп
определяется числом этих разновидностей. Таковы, например, группировки банков
по виду деятельности (депозитарные, кредитные, ипотечные).
Но нередки случаи, когда качественный
признак имеет большое число разновидностей, и перечислить их все не
представляется целесообразным. В таких случаях разрабатывают классификацию
разновидностей, т.е. сходные по своим особенностям разновидности объединяются в
группы (классы).
Под классификацией обычно понимается
устойчивая номенклатура классов и групп, образованных на основе сходства и
различия единиц изучаемого объекта.
Используются классификации в течение
длительного времени, хотя со временем, отразив происходящие изменения в объекте
наблюдения, классификации могут подвергаться более или менее существенным
изменениям. Утверждаются классификации, как правило, в качестве национального
или международного стандарта. Любая классификация может состоять из нескольких
уровней, т.е. выделенная на первом этапе классификационная группа может в дальнейшем
детализироваться и т.д.
Необходимость и степень детализации
классификационных групп определяется целью и задачами статистического
исследования.
Всестороннее статистическое изучение
социально-экономических процессов и явлений наиболее плодотворно в том случае,
если в основе его лежит система группировок. Система группировок - это ряд
взаимосвязанных статистических группировок по наиболее существенным признакам,
всесторонне отражающим важнейшие стороны изучаемых явлений.
1.5. Техника выполнения группировок
При составлении структурных
группировок на основе варьирующих количественных признаков необходимо
определить количество групп и интервалы группировки.
Интервал - количественное значение,
отделяющее одну единицу (группу) от другой, т.е. он очерчивает количественные
границы группы.
Как правило, величина интервала
представляет собой разность между максимальным и минимальным значениями
признака в каждой группе.
Вопрос о количестве групп и величине
интервала следует решать с учетом множества обстоятельств, прежде всего, исходя
из целей исследования, значения изучаемого признака и т.д.
Количество групп и величина интервала
связаны между собой: чем больше образовано групп, тем меньше интервал, и
наоборот. Количество групп зависит от числа единиц исследуемого объекта и
степени колеблемости группировочного признака. При небольшом объеме
совокупности нельзя образовывать большое число групп, так как группы будут
малочисленными.
При определении количества групп
необходимо стремиться к тому, чтобы были учтены особенности изучаемого явления.
Поэтому количество групп должно быть оптимальным, в каждую группу должно
входить достаточно большое число единиц совокупности, что отвечает требованию
закона больших чисел. Однако, в отдельных случаях представляют интерес и малочисленные
группы: новое, передовое, пока не оно станет массовым, проявляется в
незначительном числе фактов; поэтому задача статистики - выделить эти факты,
изучить их.
Таким образом, при решении вопроса о
численности единиц в группах нужно руководствоваться не формальными признаками,
а знанием сущности изучаемого явления.
На количество выделяемых групп существенное влияние оказывает степень
колеблемости группировочного признака: чем она больше, тем больше следует
образовывать групп. Ориентировочно определить оптимальное количество групп с
равными интервалами можно по формуле американского ученого Стерджесса:
n=1+3,322 lgN,
где N - число единиц совокупности.
Используя эту формулу получим
следующее соотношение:
Таблица
1
|
N
|
15-24
|
25-44
|
45-89
|
90-179
|
180-359
|
360-719
|
|
n
|
5
|
6
|
7
|
8
|
9
|
10
|
Формула Стерджесса пригодна при
условии, что распределение единиц совокупности по заданному признаку
приближается к нормальному, и при этом применяются равные интервалы в группах.
Чтобы получить группы, адекватные действительности, необходимо
руководствоваться сущностью изучаемого явления. Интервалы могут быть равные и
неравные. При исследовании экономических явлений могут применяться неравные
(прогрессивно возрастающие или прогрессивно убывающие) интервалы.
Это объясняется тем, что
количественные изменения размера признака имеют неодинаковые значения в низших
и высших по размеру признака группах: изменение количества работающих на 50-100
человек имеет существенное значение для мелких предприятий, а для крупных - не
имеет.
Группировки с равными интервалами
целесообразны в тех случаях, когда вариация проявляется в сравнительно узких
границах и распределение является практически равномерным (например, при
группировке рабочих одной профессии по размеру заработной платы, посевов пшеницы
- по урожайности).
Для группировок с равными интервалами
величина интервала составляет
i= (xmax-xmin)/n ( 1)
где xmax, xmin - наибольшее и
наименьшее значение признака соответственно;
n - число групп.
Если в результате деления получится
дробное число и возникнет необходимость в округлении, то округлять нужно, как
правило, в большую сторону.
Интервалы групп могут быть открытыми
и закрытыми.
В закрытых интервалах указаны нижняя
и верхняя границы интервала.
В открытых интервалах указана лишь
одна из границ (первый или последний интервалы). Величина открытых интервалов
принимается равной величине смежных с ними интервалов.
При анализе разнородных данных,
например, при анализе материала, собранного в различные периоды времени,
относящегося к различным отраслям промышленности, возникает необходимость
применения вторичной группировки.
Вторичная группировка - образование
новых групп на основе ранее осуществленной группировки.
Получение новых групп на основе
имеющихся возможно двумя способами перегруппировки: объединение первоначальных
интервалов путем их укрупнения и долевой перегруппировкой на основе закрепления
за каждой группой определенной доли единиц совокупности.
2. Расчетная
часть
Вариант 13
Задание 1
По
исходным данным таблицы 1:
1.
Постройте статистический ряд распределения российских банков по признаку пассивы,
образовав пять групп с равными интервалами.
2. Постройте графики полученного ряда
распределения. Графически определите значение моды и медианы.
3.
Рассчитайте характеристики интервального ряда распределения: среднюю
арифметическую, среднее квадратическое отклонение, коэффициент вариации.
4.
Вычислите среднюю арифметическую по исходным данным, сравните ее с аналогичным
показателем, рассчитанным в п.3 для интервального ряда распределения. Объясните
причину их расхождения.
Сделайте
выводы по результатам выполнения задания.
Таблица 1 –
Механистическая выборка данных о деятельности российских банков за год,
млн.руб.
|
№ предприятия
|
Пассивы
|
Работающие активы
|
|
1
|
31 551
|
25946
|
|
2
|
29 428
|
26118
|
|
3
|
6 073
|
5728
|
|
4
|
11 759
|
10085
|
|
5
|
16 415
|
17213
|
|
6
|
4 875
|
4378
|
|
7
|
8 801
|
9387
|
|
8
|
12 819
|
11908
|
|
9
|
9 500
|
7560
|
|
10
|
15 418
|
14389
|
|
11
|
17 746
|
15676
|
|
12
|
14 823
|
14389
|
|
13
|
16 596
|
15076
|
|
14
|
31 011
|
28089
|
|
15
|
10 629
|
10146
|
|
16
|
5 822
|
4780
|
|
17
|
8 734
|
7024
|
|
18
|
11 392
|
10668
|
|
19
|
7 463
|
6585
|
|
20
|
16 995
|
14228
|
|
21
|
15 035
|
14691
|
|
22
|
31 768
|
29243
|
|
23
|
13 343
|
11971
|
|
24
|
25 030
|
21902
|
|
25
|
10 816
|
10225
|
|
26
|
29 196
|
24888
|
|
27
|
23 334
|
21337
|
|
28
|
22 101
|
20968
|
|
29
|
14 770
|
14124
|
|
30
|
19 025
|
17691
|
|
31
|
4 677
|
4492
|
|
32
|
20 210
|
18785
|
|
33
|
10 234
|
9350
|
|
34
|
10 752
|
7442
|
|
35
|
10 737
|
10038
|
|
36
|
4 903
|
4296
|
Рассчитаем величину
интервала группировки по следующей формуле:
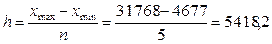 млн.руб.
млн.руб.
где xmax, xmin
- наибольшее и наименьшее значение признака соответственно; n - число групп.
Разделим банки по величине
пассивов на пять групп, величину интервала групп примем 5418,2 млн.руб. В
результате разбивки получим следующую группировку банков.
Таблица 2
– Группировка банков по величине пассивов
|
Группы банков по величине пассивов, млн.руб.
|
Число банков, единиц
|
Средняя величина пассивов, млн.руб.
|
Число банков, % к итогу
|
Накопленная частота
|
|
4 677 – 10 095,2
|
9
|
6 760,9
|
25,0
|
9,0
|
|
10 095,2 – 15 513,4
|
13
|
12 502,1
|
36,1
|
22,0
|
|
15 513,4 – 20 931,6
|
6
|
17 831,2
|
16,7
|
28,0
|
|
20 931,6 – 26 349,8
|
3
|
23 488,3
|
8,3
|
31,0
|
|
26 349,8 – 31 768
|
5
|
30 590,8
|
13,9
|
36,0
|
|
Итого
|
36
|
15 382,8
|
100,0
|
|
Как видно
из таблицы, наибольшее число банков в общем объеме (36,1%) имеют величину
пассивов на уровне 10095 – 15513 млн.руб.,
причем средняя величина пассивов этой группы составляет 12502,1 млн.руб. В
среднем величина пассивов в банках – 15382,8 млн.руб., доля банков, входящих в
группу с наибольшей величиной пассивов (13,9%) ниже доли банков, входящих в
группу с наименьшей величиной пассивов (25,0% в общем объеме).
Построим ряд
распределения, и отобразим его графически с помощью гистограммы.
|
Интервал
|
4677 - 10095,2
|
10095,2 - 15513,4
|
15513,4 - 20931,6
|
20931,6 - 26349,8
|
26349,8 - 31768
|
|
Частота
|
9,0
|
13,0
|
6,0
|
3,0
|
5,0
|
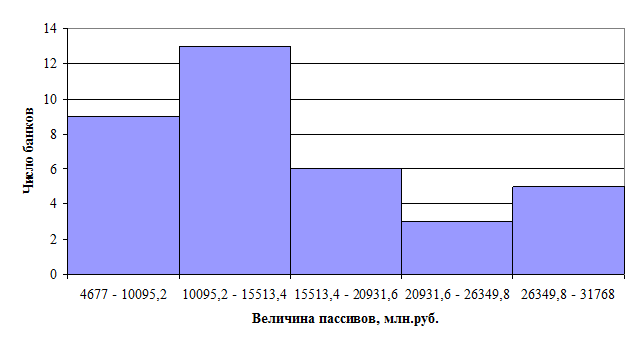
Рис. 1. Гистограмма распределения банков по величине пассивов
2) Определим графически
значение моды и медианы:
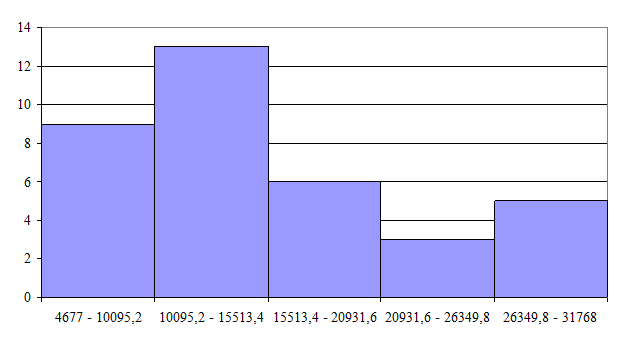
Рис. 2 –
Графическое нахождение моды


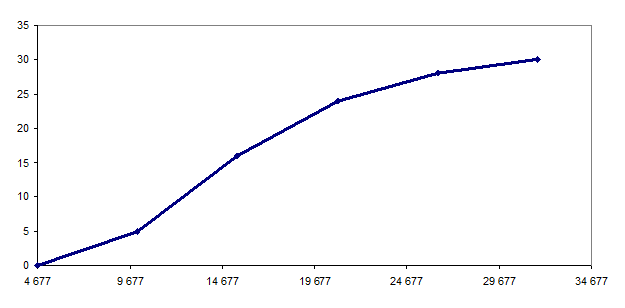
Рис. 3 – Графическое нахождение медианы
Медиана (Ме)
– это вариант, который находится а середине вариационного ряда. Медиана делит
ряд на две равные (по числу наблюдений) части.
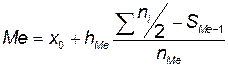 , (3)
, (3)
где х0 – нижняя
граница медианного интервала (накопленная частота которого превышает половину
общей суммы частот);
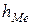 – величина медианного
интервала;
– величина медианного
интервала; 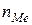 – частота медианного
интервала;
– частота медианного
интервала;
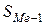 – накопленная частота
интервала, предшествующего медианному
– накопленная частота
интервала, предшествующего медианному
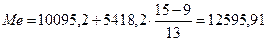 млн. руб.
млн. руб.
Модой (Мо)
вариационного ряда называется вариант, которому соответствует наибольшая
частота.
Для вычисления моды в
интервальном ряду сначала находится модальный интервал, имеющий наибольшую
частоту, а значение моды определяется линейной интерполяцией:
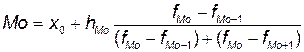 , (4)
, (4)
где хо – нижняя граница модального интервала;
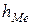 – величина модального
интервала;
– величина модального
интервала;
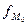 ,
, 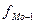 ,
, 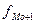 – частота ni
модального, до и послемодального интервала.
– частота ni
модального, до и послемодального интервала.
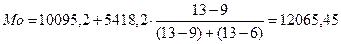 млн руб.
млн руб.
Из рисунков 2 и 3 видно,
что медиана и мода ряда распределения соответствуют расчетным, и равны 12595,9
и 12065,5 млн. руб. соответственно.
3) Рассчитаем
характеристики ряда распределения:
o средняя
арифметическая взвешенная определяется по формуле 5.
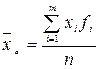 , (5)
, (5)
где xi
– варианты или середины интервалов вариационного ряда;
fi – соответствующая частота;
n – количество вариантов в вариационном ряду (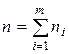 ).
).
Промежуточные
расчеты представим в таблице 4.
Таблица
4 - Промежуточные расчеты для определения средней взвешенной и среднего квадратического отклонения
|
Группы банков по величине пассивов, млн.руб.
|
Число банков, единиц
|
Середина интервала
х`i
|
x`i*fi
|
x`i - xср
|
(x`i - xср)2
|
(x`i - xср)2*fi
|
|
4677 - 10095,2
|
9
|
7386
|
66 475
|
-8 127
|
66053005
|
594477048
|
|
10095,2-15513,4
|
13
|
12804
|
166 456
|
-2 709
|
7339223
|
95409897
|
|
15513,4-20931,6
|
6
|
18223
|
109 335
|
2 709
|
7339223
|
44035337
|
|
20931,6-26349,8
|
3
|
23641
|
70 922
|
8 127
|
66053005
|
198159016
|
|
26349,8 - 31768
|
5
|
29059
|
145 295
|
13 546
|
183480570
|
917402851
|
|
Итого
|
36
|
|
558 482
|
|
330265026
|
1849484148
|
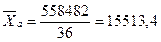 млн.руб.
млн.руб.
Среднее
квадратическое отклонение определяется по формуле 6.
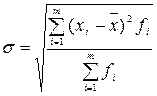 (6)
(6)
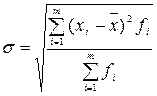 =√1849484148 / 36 =√51374559,67 =7167,6 млн. руб.
=√1849484148 / 36 =√51374559,67 =7167,6 млн. руб.
Т.е.
на 7167,6 млн.руб. в среднем величина пассивов отклоняется от среднего значения.
Коэффициент
вариации определяется по формуле 7.
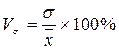 (7)
(7)
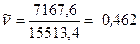 или 46,2%
или 46,2%
На
основании полученного коэффициента можно сделать вывод, что по величине
пассивов банки являются неоднородными, так как коэффициент вариации превышает
33%.
Арифметическая
средняя простая по таблице 1 будет составлять:
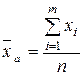 . (8)
. (8)
где xi – варианты или середины
интервалов вариационного ряда;
n – количество
вариантов в вариационном ряду (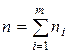 ).
).
Исходя
из наших данных: 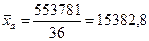 млн. руб.
млн. руб.
Расхождения между арифметической средней простой и взвешенной
произошло, так как арифметическая средняя взвешенная считалась по
сгруппированным данным.
Задание 2
По исходным данным
таблицы 1:
1. Установить наличие и характер связи
между величиной пассивов и работающих активов, образовав пять групп с равными
интервалами по обоим признакам, методами:
а) аналитической
группировки;
б) корреляционной
таблицы.
2. Измерить тесноту корреляционной связи
между названными признаками с использованием коэффициента детерминации и
эмпирического корреляционного отношения. Сделать выводы.
Решение.
1. Выявим наличие и характер связи между
величиной пассивов и работающих активов методом аналитической группировки,
образовав пять групп с равными интервалами по обоим признакам.
Из таблицы 5 выявляется следующая
закономерность – рост величины пассивов по банкам сопровождается увеличением величины
работающих активов.
Таблица
5 – Группировка банков по величине активов и пассивов, млн.руб.
|
Группы банков по величине пассивов, млн.руб.
|
Число банков
|
в среднем на один банк
|
|
Величина пассивов, млн.руб.
|
Величина активов, млн.руб.
|
|
4677 - 10095,2
|
9
|
6 760,9
|
6 025,6
|
|
10095,2 - 15513,4
|
13
|
12 502,1
|
11 494,3
|
|
15513,4 - 20931,6
|
6
|
17 831,2
|
16 444,8
|
|
20931,6 - 26349,8
|
3
|
23 488,3
|
21 402,3
|
|
26349,8 - 31768
|
5
|
30 590,8
|
26 856,8
|
|
Итого
|
36
|
15 382,8
|
13 911,6
|
Выявим наличие и характер связи между величиной
пассивов и работающих активов методом корреляционной таблицы, образовав пять
групп с равными интервалами по обоим признакам.
Рассчитаем величину
интервала группировки банков по величине активов:
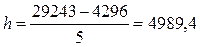 млн руб.
млн руб.
Таблица 6 - Распределение банков по сумме активов и
пассивов, млн.руб.
|
Группы банков по величине пассивов, млн.руб., Y
|
Группы банков по величине активов, млн.руб. Х
|
Число бан-ков, fy
|
|
xi
|
4296 - 9285
|
9285- 14275
|
14275-19264
|
19264-24254
|
24254-29243
|
|
yi
|
6791
|
11780
|
16770
|
21759
|
26748
|
|
4677 - 10095
|
7386
|
8
|
1
|
0
|
0
|
0
|
9
|
|
10095 - 15513
|
12804
|
1
|
9
|
3
|
0
|
0
|
13
|
|
15513 - 20932
|
18223
|
0
|
1
|
5
|
0
|
0
|
6
|
|
20932 - 26350
|
23641
|
0
|
0
|
0
|
3
|
0
|
3
|
|
26350 - 31768
|
29059
|
0
|
0
|
0
|
0
|
5
|
5
|
|
Число банков, fx
|
|
9
|
11
|
8
|
3
|
5
|
36
|
Как
следует из корреляционной таблицы, между изучаемыми признаками существует прямая
связь, поскольку с ростом величины пассивов по банкам величина активов также увеличивается.
Таблица 7 – Промежуточные расчеты внутригрупповой дисперсии
|
Группы банков по величине пассивов, млн.руб., Y
|
|
№ п/п
|
3475 - 5415
|
5415 - 7355
|
7355 - 9295
|
9295 - 11235
|
11235 - 13175
|
|
X
|
(x-xсрi)2
|
X
|
(x-xсрi)2
|
X
|
(x-xсрi)2
|
X
|
(x-xсрi)2
|
X
|
(x-xсрi)2
|
|
1
|
4492
|
2351792,6
|
9350
|
4598055,5
|
17213
|
590080
|
20968
|
188645,44
|
24888
|
3876173,4
|
|
2
|
4378
|
2714439,3
|
10146
|
1817933,6
|
15076
|
1873705
|
21337
|
4268,44
|
26118
|
545825,4
|
|
3
|
4296
|
2991362,4
|
10038
|
2120832,1
|
14228
|
4914350
|
21902
|
249666,78
|
28089
|
1518316,8
|
|
4
|
4780
|
1551408,6
|
7442
|
16421197,6
|
15676
|
591105
|
|
|
25946
|
829556,6
|
|
5
|
5728
|
88539,3
|
10225
|
1611142,0
|
17691
|
1552931
|
|
|
29243
|
5693950,4
|
|
6
|
6585
|
312978,1
|
10668
|
682784,4
|
18785
|
5476380
|
|
|
|
|
|
7
|
7024
|
996891,3
|
10085
|
1986148,2
|
|
|
|
|
|
|
|
8
|
9387
|
11299308,8
|
11908
|
171141,3
|
|
|
|
|
|
|
|
9
|
7560
|
2354519,8
|
11971
|
227235,6
|
|
|
|
|
|
|
|
10
|
|
|
14124
|
6915281,6
|
|
|
|
|
|
|
|
11
|
|
|
14389
|
8379243,6
|
|
|
|
|
|
|
|
12
|
|
|
14691
|
10218841,7
|
|
|
|
|
|
|
|
13
|
|
|
14389
|
8379243,6
|
|
|
|
|
|
|
|
Σ
|
54230
|
24661240,2
|
149426
|
63529080,8
|
98669
|
14998550,8
|
64207
|
442580,7
|
134284,0
|
12463822,8
|
На
основании расчетов, выполненных в таблицах 6 и 7, определим коэффициент
детерминации и эмпирическое корреляционное отношение.
Внутригрупповая дисперсия
(σj2)
отражает вариацию, т.е. часть вариации, происходящую под влиянием неучтенных
факторов и независящую от признака – фактора, положенного в основе группировки.
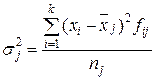
где 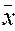 j – частная средняя по j-ой группе
(рассчитана в таблице 8);
j – частная средняя по j-ой группе
(рассчитана в таблице 8);
fj – число единиц в j-ой группе.
Таблица 8 – Результаты расчета
внутригрупповой дисперсии
|
Группы банков по величине пассивов, млн.руб.
|
Средняя величина активов, . Хi
|
Число банков, fi
|
Дисперсия затрат
|
|
|
|
|
4677 - 10095,2
|
6025,6
|
9
|
2740137,80
|
|
|
10095,2 - 15513,4
|
11494,3
|
13
|
4886852,37
|
|
|
15513,4 - 20931,6
|
16444,8
|
6
|
2499758,47
|
|
|
20931,6 - 26349,8
|
21402,3
|
3
|
147526,89
|
|
|
26349,8 - 31768
|
26856,8
|
5
|
2492764,56
|
|
Средняя
дисперсия из групповых (σср2) определяется по
следующей формуле:
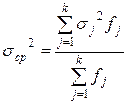
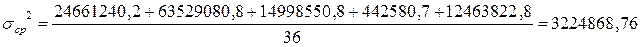
Вариацию между группами за счет признака-фактора,
положенного в основу группировки, отражает межгрупповая дисперсия:
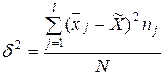
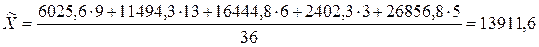
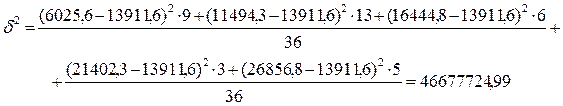
Общая дисперсия
рассчитывается по следующей формуле
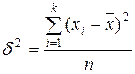
Таблица 9 –
Расчет общей дисперсии
|
Работающие активы,
млн. руб.
|
x-xср
i
|
(x-xср
i)2
|
|
4492
|
-9419,6
|
88728026,9
|
|
4378
|
-9533,6
|
90888681,5
|
|
4296
|
-9615,6
|
92458908,6
|
|
4780
|
-9131,6
|
83385306,9
|
|
5728
|
-8183,6
|
66970581,5
|
|
6585
|
-7326,6
|
53678416,3
|
|
7024
|
-6887,6
|
47438421,5
|
|
9387
|
-4524,6
|
20471603,0
|
|
7560
|
-6351,6
|
40342258,0
|
|
9350
|
-4561,6
|
20807789,1
|
|
10146
|
-3765,6
|
14179408,6
|
|
10038
|
-3873,6
|
15004432,6
|
|
7442
|
-6469,6
|
41855149,1
|
|
10225
|
-3686,6
|
13590691,9
|
|
10668
|
-3243,6
|
10520652,6
|
|
10085
|
-3826,6
|
14642527,4
|
|
11908
|
-2003,6
|
4014234,9
|
|
11971
|
-1940,6
|
3765755,9
|
|
14124
|
212,4
|
45132,6
|
|
14389
|
477,4
|
227953,2
|
|
14691
|
779,4
|
607533,6
|
|
14389
|
477,4
|
227953,2
|
|
17213
|
3301,4
|
10899535,4
|
|
15076
|
1164,4
|
1355930,9
|
|
14228
|
316,4
|
100137,1
|
|
15676
|
1764,4
|
3113264,2
|
|
17691
|
3779,4
|
14284200,3
|
|
18785
|
4873,4
|
23750460,8
|
|
20968
|
7056,4
|
49793408,2
|
|
21337
|
7425,4
|
55137225,2
|
|
21902
|
7990,4
|
63847202,4
|
|
24888
|
10976,4
|
120482332,6
|
|
26118
|
12206,4
|
148997286,0
|
|
28089
|
14177,4
|
200999931,0
|
|
25946
|
12034,4
|
144827853,1
|
|
29243
|
15331,4
|
235053188,8
|
|
Итого
|
|
1796493374,9
|
σ02= 1796493374,9/ 36 = 49902593,75
Проверим общую дисперсию правилом сложения:
σ02 = σср2 + δ2 = 3224868,76 + 46677724,99
= 49902593,75
Коэффициент детерминации
равен отношению межгрупповой дисперсии к общей и показывает долю общей вариации
результативного признака, обусловленного вариацией группировочного признака:
η2 = δ2
/σ 02
где η2 – коэффициент
детерминации.
η2 = 46677724,99 / 49902593,75= 0,935 или 93,5%
Из расчетов следует, что
на 93,5% вариация работающих активов обусловлена различиями величины пассивов.
Эмпирическое корреляционное отношение:
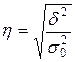
где η - эмпирическое корреляционное отношение.
По данным задачи
эмпирическое корреляционное отношение равно:
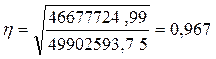
Эмпирическое
корреляционное отношение составляет 0,967, что согласно оценки по шкале
Чэддока, соответствует очень сильной связи между признаками.
Задание
3
По результатам выполнения
задания 1 с вероятностью 0,954 определить:
·
Ошибку
выборки средней величины пассивов банков, в которых будет находиться средняя величина в
генеральной совокупности.
·
Ошибку
выборки доли банков с величиной пассивов 12819 млн. руб. и более и границы, в
которых будет находиться генеральная доля.
Решение
1) Средняя ошибка выборки
при 3%-ой бесповторной выборке определяется по следующей формуле:
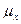 =
= 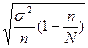 (15)
(15)
где σ 2 - дисперсия выборочной совокупности
(определена в задаче 1); n – объем выборочной совокупности;
N – объем генеральной совокупности.
и составит: 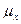 =
= 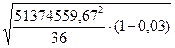 = 1176,55 млн руб.
= 1176,55 млн руб.
Предельная ошибка выборки с
вероятностью 0,954 (t=2): Δх
= t*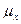 и составит: Δх =1176,55*2 = 2353,1 млн. руб. Тогда можно
утверждать, что при заданной вероятности генеральная средняя будет находиться в
следующих пределах:
и составит: Δх =1176,55*2 = 2353,1 млн. руб. Тогда можно
утверждать, что при заданной вероятности генеральная средняя будет находиться в
следующих пределах:
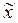 – Δx ≤
– Δx ≤ 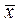 ≤
≤ 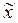 + Δx (16)
+ Δx (16)
или 13029,71 ≤ 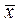 ≤ 17735,90 млн.руб.
≤ 17735,90 млн.руб.
2)
Выборочная
доля w, или частность, определяется отношением числа единиц, обладающих
изучаемым признаком m, к общему числу единиц выборочной совокупности n:
w = m/n
(17)
Предельная
ошибка для доли при бесповторном случайном и механическом отборе рассчитывают по следующим
формулам:
Δw = t 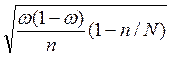 (18)
(18)
где Δw – предельная ошибка для доли.
Доля банков с величиной пассивов
12819 млн. руб. и более составляет: w = 20 / 36 = 0,56
Предельная ошибка для доли: Δw = 2* 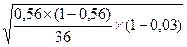 = 0,163
= 0,163
Границы
генеральной доли рассчитываются по формуле:
w
– Δw
≤ w
≤ w
+ Δw (19)
0,39
≤ w
≤ 0,72
С вероятностью 0,954 можно утверждать,
что удельный вес банков с величиной пассивов 12819 млн. руб. и более будет
находится в пределах 55,5% 16,3% или 39,2% ≤ w
≤ 71,9% в генеральной совокупности.
16,3% или 39,2% ≤ w
≤ 71,9% в генеральной совокупности.
Задание 4
Динамика остатков средств физических
лиц на счетах банка на 1 января характеризуется следующими данными:
|
Год
|
Остаток средств на счетах
|
Курс доллара США, руб.
|
|
рублевых, млн.руб.
|
валютных, тыс.долларов США
|
|
2000
|
1984
|
24305
|
27,00
|
|
2001
|
2386
|
28446
|
28,16
|
|
2002
|
3362
|
43825
|
30,67
|
|
2003
|
4836
|
64317
|
31,78
|
|
2004
|
7695
|
69330
|
29,45
|
1. Определить остаток
средств на всех счетах (рублевых и валютных) в рублях и по этому показателю
рассчитать:
а) абсолютные приросты (базисные и
цепные);
б) темпы роста и прироста (базисные и
цепные);
Результаты расчетов представить в
таблице.
в) среднегодовой темп роста.
2. Построить график динамики остатков
средств на всех счетах физических лиц в национальной валюте.
3. Произвести факторный анализ
динамики остатков средств в национальной валюте на валютных счетах, рассчитав
абсолютный прирост остатков средств на 1 января 2004 г. по сравнению с 1 января
2003 г. за счет изменения:
а) курса доллара;
б) остатка средств на счетах.
Сделать выводы.
Определим остаток средств на всех
счетах (рублевых и валютных) в рублях сложив сумму остатков на рублевых счетах
и сумму остатков на валютных счетах, пересчитав их в национальной валюте по
среднегодовому курсу доллара США.
Рассчитаем базисные и цепные темпы
роста и прироста по формулам:
– цепные темпы
роста, когда каждый уровень ряда
сопоставляется с предшествующим ему уровнем:
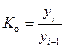 ,
,
– базисные темпы роста,
когда все уровни ряда сопоставляются с одним и тем же уровнем y0, выбранным за базу сравнения:
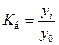 .
.
– базисные темпы
прироста:
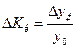
 .
.
– цепные темпы прироста:
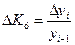 .
.
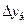 и
и 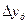 - абсолютный базисный или цепной прирост;
- абсолютный базисный или цепной прирост;
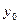 - уровень ряда динамики,
выбранный за базу для определения базисных абсолютных приростов;
- уровень ряда динамики,
выбранный за базу для определения базисных абсолютных приростов;
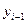 - уровень ряда
динамики, выбранный за базу для определения i-го цепного абсолютного прироста.
- уровень ряда
динамики, выбранный за базу для определения i-го цепного абсолютного прироста.
Сведем результаты расчета в таблицу.
Таблица 11 – Результаты расчета.
|
Год
|
Общий остаток средств, млн. руб.
|
Абсолютный прирост, млн.руб.
|
Темп роста, %
|
Темп прироста, %
|
|
базисный
|
цепной
|
базисный
|
цепной
|
базисный
|
цепной
|
|
2000
|
2640,2
|
0,0
|
0,0
|
100,0
|
100,0
|
0,0
|
0,0
|
|
2001
|
3187,0
|
546,8
|
546,8
|
120,7
|
120,7
|
20,7
|
20,7
|
|
2002
|
4706,1
|
2065,9
|
1519,1
|
178,2
|
147,7
|
78,2
|
47,7
|
|
2003
|
6880,0
|
4239,8
|
2173,9
|
260,6
|
146,2
|
160,6
|
46,2
|
|
2004
|
9736,8
|
7096,5
|
2856,8
|
368,8
|
141,5
|
268,8
|
41,5
|
Среднегодовой
темп роста можно определить, пользуясь формулой:
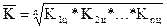
где n - число
рассчитанных цепных или базисных темпов роста;
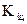 - цепные темпы роста.
- цепные темпы роста.
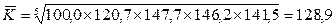
Построим график динамики остатков
средств на всех счетах физических лиц в национальной валюте.
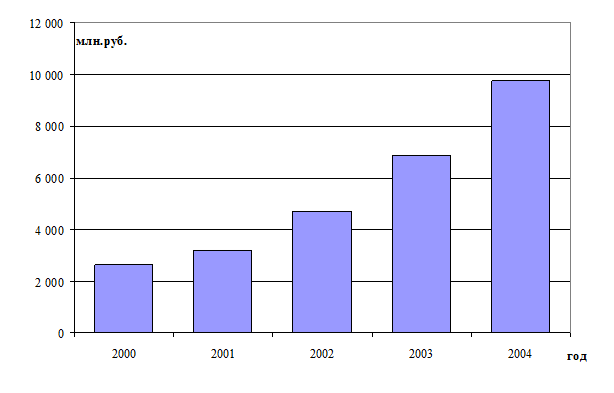
Рассмотрим динамику остатков средств
в национальной валюте на валютных счетах. Абсолютный прирост остатков средств
на 1 января 2004 г. по сравнению с 1 января 2003 г. составило
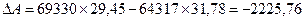 тыс.руб.
тыс.руб.
На изменение величины остатков в
национальной валюте оказали влияние два фактора: остаток средств на счетах и
изменение курса доллара США. Определим влияние этих факторов.
Влияние изменения остатков на счетах
составило:
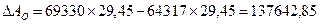 тыс.руб.
тыс.руб.
Влияние изменения курса доллара США
составило:
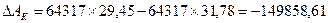 тыс.руб.
тыс.руб.
Осуществим проверку:
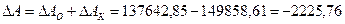 тыс.руб.
тыс.руб.
Таким образом, на 1 января 2004 г. на
валютных счетах остатки в национальной валюте были на 2225, 76 тыс.руб. меньше,
чем на 1 января 2003 г. Данное снижение было вызвано падением курса доллара
США, которое снизило сумму в рублях на 149,9 млн.руб. В долларах же остатки на
валютных счетах выросли. Если бы курс доллара США остался на уровне 1 января
2003 г., то остатки в национальной валюте также возросли бы на 137,6 млн.руб.
Общие же остатки на всех счетах в
национальной валюте выросли за счет значительного увеличения остатков на
рублевых счетах.
3. АНАЛИТИЧЕСКАЯ
ЧАСТЬ
3.1. Постановка задачи
По исходным данным о
банках, представленным в таблице 12, произвести группировку 20 банков по
величине кредитных вложений. Подобрать 3-4 наиболее экономически связанных и
существенных показателя, определить их суммарные величины по каждой группе, а
также вычислить показатели в относительном выражении. Результаты группировки
изложить в сводной групповой таблице.
Для группировки банков с
помощью аналитической группировки проанализировать зависимость величины
кредитных вложений от других экономических показателей, характеризующих
деятельность банков.
Таблица 12 – Данные о деятельности
коммерческих банков, млн.руб.
|
Номер банка
|
Кредитные вложения
|
Суммарный риск
|
Чистые активы
|
Суммарные обязательства
|
Прибыль
|
|
1
|
0
|
952
|
944
|
820
|
6
|
|
2
|
258
|
325
|
421
|
251
|
85
|
|
3
|
241
|
422
|
425
|
320
|
10
|
|
4
|
236
|
258
|
458
|
251
|
29
|
|
5
|
751
|
952
|
1152
|
1111
|
25
|
|
6
|
625
|
1145
|
1478
|
1521
|
300
|
|
7
|
421
|
581
|
721
|
521
|
6
|
|
8
|
853
|
952
|
952
|
800
|
19
|
|
9
|
41
|
452
|
521
|
400
|
41
|
|
10
|
451
|
752
|
752
|
630
|
14
|
|
11
|
87
|
152
|
125
|
45
|
1
|
|
12
|
251
|
281
|
325
|
251
|
11
|
|
13
|
236
|
325
|
581
|
451
|
36
|
|
14
|
251
|
210
|
412
|
332
|
35
|
|
15
|
45
|
178
|
214
|
95
|
41
|
|
16
|
325
|
331
|
352
|
258
|
5
|
|
17
|
285
|
400
|
451
|
332
|
32
|
|
18
|
251
|
422
|
710
|
521
|
15
|
|
19
|
352
|
399
|
452
|
335
|
13
|
|
20
|
102
|
105
|
114
|
0
|
9
|
Источник:
Бюллетень банковской статистики, 2006, № 6.
3.2. Методика решения задачи
Используя номограмму по
формуле Стерджесса, определяем, что для 20 банков (N) оптимальное количество
групп (m) составляет пять.
Таблица 13 – Номограмма по формуле
Стерджесса
|
N
|
15¸24
|
25¸44
|
45¸89
|
90¸179
|
180¸359
|
360¸719
|
720¸1489
|
|
m
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
Поскольку вариация
признака происходит в сравнительно узких границах и распределение носит
равномерный характер, то построим группировку с равными интервалами по признаку
кредитных вложений:
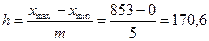 ,
,
где h – величина интервала;
xmax, xmin
– максимальное и минимальное значения группировочного признака в совокупности; m – число групп.
Определим количество
банков по группам при построении группировки с полученным интервалом, также
рассчитаем суммарное значение других представленных показателей, и их
относительное значение по группе. Результаты расчета представим в таблице 14.
3.3. Технология выполнения компьютерных расчетов
Расчеты выполняются в
табличном процессоре MS Excel. Расположение исходных данных для
расчетов представлено на рис. 5, а формульный шаблон группировочной таблицы и
формула расчета интервала на рис. 6.
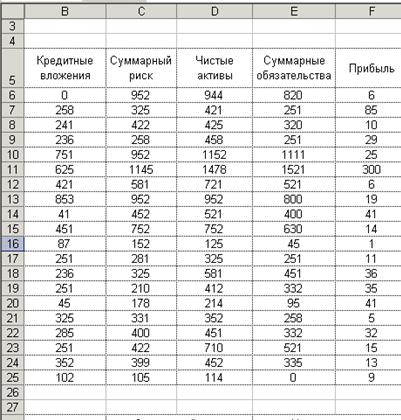
Рис. 5.
Расположение исходных данных на листе MS Excel
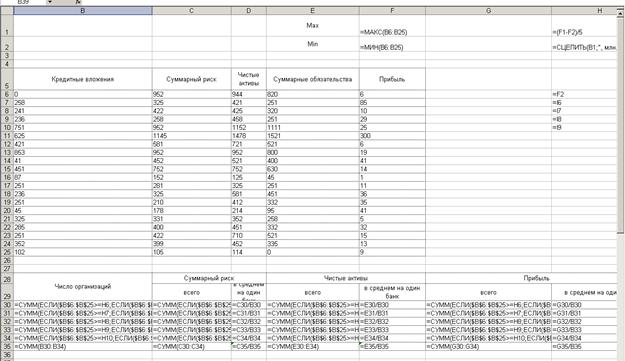
Рис. 6.
Расположение формульного шаблона группировочной таблицы
на листе MS Excel
Таблица 14 – Сводная
групповая таблица, млн.руб.
|
Группы банков по кредитным вложениям
|
Число органи-заций
|
Суммарный риск
|
Чистые активы
|
Прибыль
|
|
всего
|
в среднем на один банк
|
всего
|
в среднем на один банк
|
всего
|
в среднем на один банк
|
|
0 - 170,6
|
5
|
1839
|
367,8
|
1918
|
383,6
|
98
|
19,6
|
|
170,6 - 341,2
|
9
|
2974
|
330,4
|
4135
|
459,4
|
258
|
28,7
|
|
341,2 - 511,8
|
3
|
1732
|
577,3
|
1925
|
641,7
|
33
|
11,0
|
|
511,8 - 682,4
|
1
|
1145
|
1145,0
|
1478
|
1478,0
|
300
|
300,0
|
|
682,4 - 853
|
2
|
1904
|
952,0
|
2104
|
1052,0
|
44
|
22,0
|
|
Итого
|
20
|
9594
|
479,7
|
11560
|
578,0
|
733
|
36,7
|
Построим гистограмму и
кумуляту распределения коммерческих банков по величине кредитных вложений.
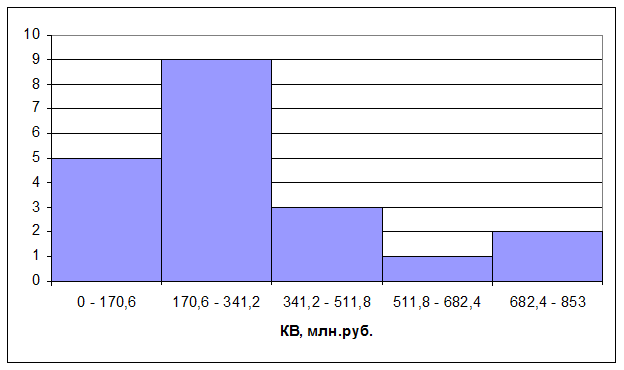
Рис.1. Гистограмма
распределения банков по величине кредитных вложений
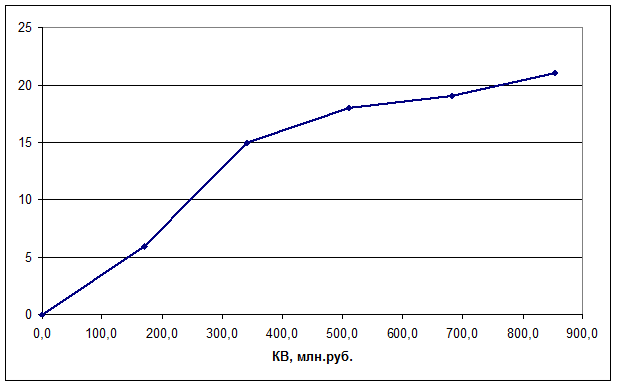
Рис.2.
Кумулята распределения банков по величине кредитных вложений
3.4. Анализ результатов статистических компьютерных расчетов
Построенная аналитическая
группировка позволяет сделать вывод, что наибольшее количество банков имеет
уровень кредитных вложений в пределах 170,6 – 341,2 млн.руб., в группы с
величиной кредитных вложений 511,8 – 682,4 млн.руб. попадает лишь один банк.
При росте величины кредитных вложений по банкам, такие показатели как суммарный
риск, чистые активы и прибыль также увеличиваются, т.е. они связаны прямо
пропорциональной связью.
На основе гистограммы
распределения банков по величине кредитных вложений можно сделать вывод, что
банки по величине кредитных вложений характеризуются концентрацией, которая
заключена в пределах величины кредитных вложений в ценные бумаги от 0 до 512
млн.руб.
ЗАКЛЮЧЕНИЕ
Сделаем краткие выводы по
всем разделам курсовой работы.
В теоретической части
курсовой рассмотрена система, показателей, характеризующих кредитную
деятельность банков. Основными их них являются объем предоставляемых кредитов
(как физическим, так и юридическим лицам), структура и качество активов,
доходность и рентабельность кредитной деятельности. Данные показатели изучаются
с помощью таких статистических методов, как метод группировок.
В расчетной части
курсовой работы был построен ряд распределения банков по признаку величина
пассивов, с образованием пяти групп с равными интервалами. По величине пассивов представленную
совокупность банков можно считать неоднородной, поскольку коэффициент вариации
превышает 33%.
Изучение взаимосвязи величины
пассивов и работающих активов банков показало, что существует прямая связь
между данными показателями, т.е. чем больше величина пассивов, тем больше
величина его работающих активов. Расчет коэффициента детерминации и
эмпирического корреляционного отношения также подтверждает тесноту связи данных
показателей.
Анализ выборочной
совокупности позволяет с вероятностью 0,954 утверждать, что предельная ошибка
выборки средней величины пассивов банков составит 1176,55 млн. руб. и генеральная средняя
будет находиться в пределах
13029,71 ≤ 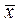 ≤ 17735,90 млн.руб. Также с вероятностью 0,954 можно утверждать,
что удельный вес банков с величиной пассивов 128119 млн. руб. и более будет
находится в пределах 55,5%
≤ 17735,90 млн.руб. Также с вероятностью 0,954 можно утверждать,
что удельный вес банков с величиной пассивов 128119 млн. руб. и более будет
находится в пределах 55,5%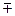 16,3% или 39,2% ≤ w
≤ 71,9% в генеральной совокупности.
16,3% или 39,2% ≤ w
≤ 71,9% в генеральной совокупности.
Анализ тесноты связи различных
показателей банков, проведенный в аналитической части, показывает, При росте
величины кредитных вложений по банкам, такие показатели как суммарный риск,
чистые активы и прибыль также увеличиваются, т.е. они связаны прямо пропорциональной
связью.
В итоге можно отметить,
что все задачи курсовой работы выполнены, цель достигнута.
СПИСОК
ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Гусаров В.М. Статистика: Учебное
пособие для вузов. – М.: ЮНИТИ-ДАНА, 2001.
2. Кажухарь Л.И. Основы общей теории
статистики. – М.: Финансы и статистика, 1999.
3. Общая теория статистики: Учебник/Под
ред. М.Р.Ефимовой. М.: ИНФРА–М, 2001.
4. Савицкая Г.В. Анализ хозяйственной
деятельности предприятия. – М.: ИНФРА-М, 2002.
5. Сироткина Т.С., Каманина А.М. Основы
теории статистики: Учеб. пособие для вузов/ Под
ред. проф. В.М. Симчеры. – М.: Финстатинформ, 1996.
6. Статистика. Методические указания по
выполнению курсовой работы. Для студентов III курса специальностей 060400 «Финансы
и кредит». – М.: Вузовский учебник, 2005.
7. Теория статистики: Учебник/Под ред.
Р.А. Шмойловой. – 3-е изд., перераб. и доп. – М.: Финансы и статистика, 2001.
8. Экономико-статистический анализ:
Учеб. пособие для вузов / С.Д. Ильенкова, Н.Д. Ильенкова, С.А. Орехов и др.;
Под ред. проф. С.Д. Ильенковой. – М.: ЮНИТИ-ДАНА, 2002.