Всероссийский заочный финансово-экономический
институт
Контрольная
работа
по дисциплине «Эконометрика»
Вариант № 22
Выполнил:
Проверил:
Тула, 2006 г.
Задание I.
Исходные данные:
|
Показатель
|
Номер
наблюдения
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
X(t)
|
75
|
77
|
73
|
70
|
66
|
63
|
67
|
63
|
61
|
1) определить
наличие тренда Y(t);
2) построить
линейную модель Y(t)=a0+a1t, параметры которой оценить с помощью
МНК;
3) оценить
адекватность построенных моделей на основе исследования:
- случайности остаточной
компоненты по критерию пиков;
- независимости уровней ряда
остатков по d-критерию
(в качестве критических используйте уровни d1=1,08 и d2=1,36) или по первому коэффициенту корреляции,
критический уровень которого r(1)=0,36;
- нормальности распределения
остаточной компоненты по R/S-критерию с критическими
уровнями 2,7-3,7;
4) для оценки точности модели
используйте среднеквадратическое отклонение и среднюю по модулю относительную
ошибку;
5) построить
точечный и интервальный прогнозы на два шага вперед (для вероятности P=70% используйте коэффициент
t=1,11)
Все расчеты проводились с использованием программы «Статэксперт»,
результаты которых представлены в виде таблиц и графиков.
1) Определение
наличия тренда.
Определим
статистики временного ряда:
|
Cтатистики временного ряда - Показатель-A
|
|
|
|
|
|
|
Базисные
характеристики
|
|
|
|
|
Наблюдение
|
Абс.
прирост
|
Темп
Роста
|
Темп
прироста
|
|
2
|
2.000
|
102.667
|
2.667
|
|
3
|
-2.000
|
97.333
|
-2.667
|
|
4
|
-5.000
|
93.333
|
-6.667
|
|
5
|
-9.000
|
88.000
|
-12.000
|
|
6
|
-12.000
|
84.000
|
-16.000
|
|
7
|
-8.000
|
89.333
|
-10.667
|
|
8
|
-12.000
|
84.000
|
-16.000
|
|
9
|
-14.000
|
81.333
|
-18.667
|
|
|
|
|
|
Цепные характеристики
|
|
|
|
|
Наблюдение
|
Абс.
прирост
|
Темп
роста
|
Темп
прироста
|
|
2
|
2.000
|
102.667
|
2.667
|
|
3
|
-4.000
|
94.805
|
-5.195
|
|
4
|
-3.000
|
95.890
|
-4.110
|
|
5
|
-4.000
|
94.286
|
-5.714
|
|
6
|
-3.000
|
95.455
|
-4.545
|
|
7
|
4.000
|
106.349
|
6.349
|
|
8
|
-4.000
|
94.030
|
-5.970
|
|
9
|
-2.000
|
96.825
|
-3.175
|
|
Средние
характеристики
|
|
|
Характеристика
|
Значение
|
|
Среднее
арифметическое
|
68.333
|
|
Средний
темп роста (%)
|
97.450
|
|
Средний
темп прироста (%)
|
-2.550
|
|
Средний
абсолютный прирост
|
-1.750
|
Результаты
проверки гипотезы об отсутствии тренда приведены в таблице:
|
Гипотеза
об отсутствии тренда
|
|
Метод проверки
|
Результат
|
|
Метод
Форстера-Стюарта
|
Да
|
|
Метод
сравнения средних
|
Нет
|
|
Вывод:
гипотеза отвергается
|
|
Приведем графики.
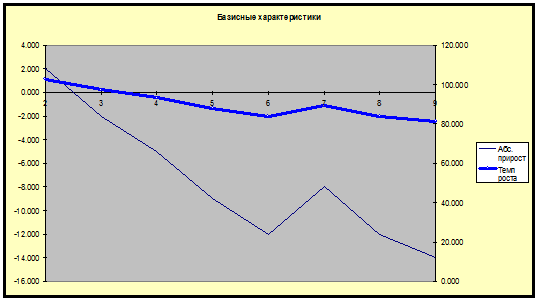
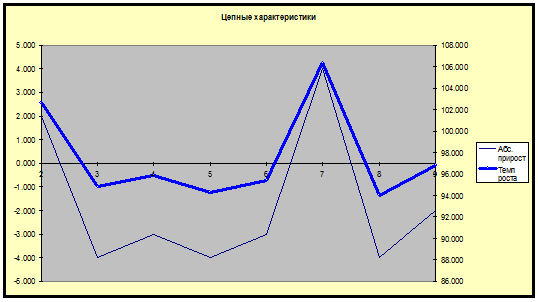
2) Построим
линейную модель.
Рассмотрим
уравнение вида 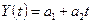 , где t
– время. С помощью данной функции будем аппроксимировать функцию, заданную
таблично с помощью метода наименьших квадратов, т.е. сумма квадратов отклонений
между теоретическими и эмпирическими уровнями:
, где t
– время. С помощью данной функции будем аппроксимировать функцию, заданную
таблично с помощью метода наименьших квадратов, т.е. сумма квадратов отклонений
между теоретическими и эмпирическими уровнями: 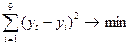 (1).
(1).
Параметры
модели 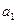 ,
, 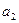 согласно методу наименьших квадратов находятся из решения
системы уравнений из преобразования (1):
согласно методу наименьших квадратов находятся из решения
системы уравнений из преобразования (1):
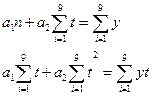
Решая эту систему, получим:
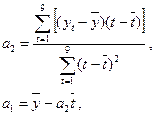
где 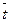 и
и 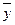 - средние значения
соответственно моментов наблюдения и уровней ряда.
- средние значения
соответственно моментов наблюдения и уровней ряда.
|
Параметры
моделей
|
|
|
|
Модель
|
a1
|
a2
|
|
Y(t)=+78.083-1.950*t
|
78.083
|
-1.950
|
3) Оценим адекватность, точность и
качество построенной модели.
|
Проверка
однородности данных
|
|
|
|
Номер наблюдения
|
Факт
|
Расчет
|
Новое
значение
|
|
7
|
67.000
|
63.250
|
67.000
|
|
Обнаружены
аномальные наблюдения!
|
|
|
|
Автокорреляционная
функция
|
|
|
|
Лаг
|
Исходный
ряд
|
Разностный
ряд (d=1)
|
|
1
|
0.641
|
-0.299
|
|
2
|
0.256
|
-0.147
|
|
Cтандартные
отклонения = +0.4658, +0.3684
|
|
|
Частная
автокорреляционная функция
|
|
|
Лаг
|
Исходный
ряд
|
Разностный
ряд (d=1)
|
|
1
|
0.809
|
-0.376
|
|
2
|
-0.262
|
-0.259
|
|
Cтандартные
отклонения = +0.3333, +0.3780
|
|
|
Таблица кривых роста
|
|
|
|
Функция
|
Критерий
|
Эластичность
|
|
Y(t)=+78.083-1.950*t
|
4.836
|
-0.143
|
|
Выбрана функция Y(t)=+78.083-1.950*t
|
|
|
Характеристики
базы моделей
|
|
|
|
Модель
|
Адекват
ность
|
Точность
|
Качество
|
|
Y(t)=+78.083-1.950*t
|
86.131
|
80.933
|
82.232
|
|
Лучшая
модель Y(t)=+78.083-1.950*t
|
|
|
4) Приведем характеристики остатков.
|
Таблица
остатков
|
|
|
|
|
|
номер
|
Факт
|
Расчет
|
Ошибка
абс.
|
Ошибка
относит.
|
|
1
|
75.000
|
76.133
|
-1.133
|
-1.511
|
|
2
|
77.000
|
74.183
|
2.817
|
3.658
|
|
3
|
73.000
|
72.233
|
0.767
|
1.050
|
|
4
|
70.000
|
70.283
|
-0.283
|
-0.405
|
|
5
|
66.000
|
68.333
|
-2.333
|
-3.535
|
|
6
|
63.000
|
66.383
|
-3.383
|
-5.370
|
|
7
|
67.000
|
64.433
|
2.567
|
3.831
|
|
8
|
63.000
|
62.483
|
0.517
|
0.820
|
|
9
|
61.000
|
60.533
|
0.467
|
0.765
|
|
Характеристики
остатков
|
|
|
Характеристика
|
Значение
|
|
Среднее
значение
|
0.000
|
|
Дисперсия
|
3.761
|
|
Приведенная
дисперсия
|
4.836
|
|
Средний
модуль остатков
|
1.585
|
|
Относительная
ошибка
|
2.327
|
|
Критерий
Дарбина-Уотсона
|
1.944
|
|
Коэффициент
детерминации
|
0.999
|
|
F
- значение ( n1 = 1, n2 = 7)
|
8737.727
|
|
Критерий
адекватности
|
86.131
|
|
Критерий
точности
|
80.933
|
|
Критерий
качества
|
82.232
|
|
Уравнение
значимо с вероятностью 0.95
|
5) Построим прогноз на 3 шага вперёд
|
Таблица
прогнозов (p = 80%)
|
|
|
|
|
Упреждение
|
Прогноз
|
Нижняя
граница
|
Верхняя
граница
|
|
1
|
58.583
|
56.318
|
60.848
|
|
2
|
56.633
|
54.004
|
59.262
|
|
3
|
54.683
|
51.680
|
57.686
|
Приведем
график прогноза:
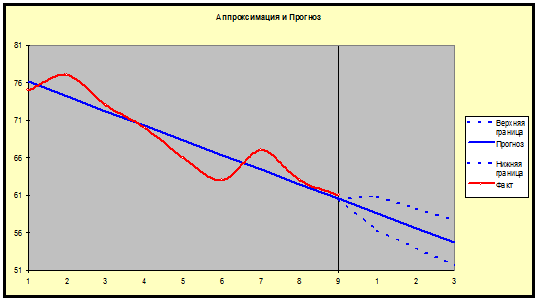
Построим
графики абсолютной и относительной ошибок:
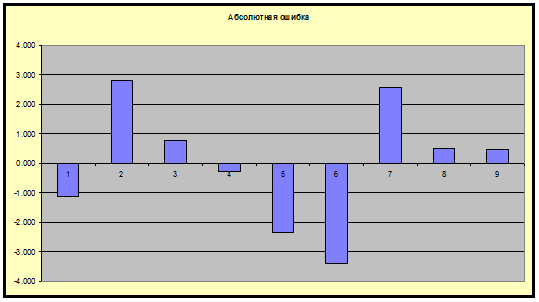
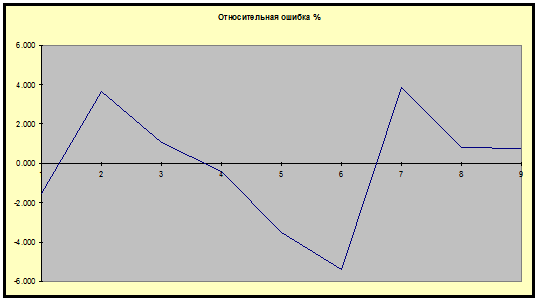
Задание II.
1) построить матрицу коэффициентов парной корреляции Y(t) с X1(t) и X2(t) и выбрать фактор, наиболее
тесно связанный с зависимой переменной Y(t).
Исходя из следующих данных:
|
Y(t)
|
X1(t)
|
X2(t)
|
|
75
|
28
|
15
|
|
77
|
34
|
20
|
|
73
|
32
|
24
|
|
70
|
36
|
30
|
|
66
|
39
|
33
|
|
63
|
42
|
37
|
|
67
|
45
|
36
|
|
63
|
41
|
40
|
|
31
|
46
|
42
|
С помощью Excel
рассчитаем матрицу парных коэффициентов корреляции переменных. Для этого
воспользуемся стандартной функцией:
1) в главном меню последовательно выбираем пункты Вставка / Функция;
2) в открывшемся окне Мастер
функций выбираем Категория:
Статистические / Функция: КОРРЕЛ;
3) заполняем Массив1
и Массив2 необходимым множеством
данных (Y(t) и X1(t), Y(t) и X2(t), X1(t) и X2(t));
4) результаты вычислений – матрица коэффициентов парной
корреляции – представлены на рис.2.1.
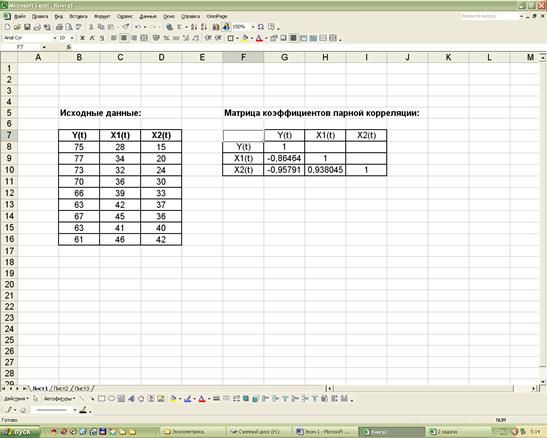
Рис. 2.1. Матрица коэффициентов парной корреляции
Коэффициент корреляции также
можно вычислить по следующей формуле:
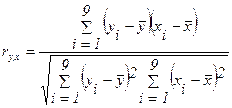 ;
;
Для удобства вычисления коэффициента корреляции ry,x1 предварительные
расчеты сведем в таблицу:
|
Наблюдение
|
Y(t)
|
X1(t)
|
(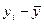 ) )
|
(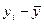 )2 )2
|
(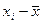 ) )
|
(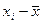 )2 )2
|
(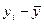 )( )(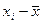 ) )
|
|
1
|
75
|
28
|
6,667
|
44,4444
|
-10,111
|
102,2346
|
-67,4074
|
|
2
|
77
|
34
|
8,667
|
75,1111
|
-4,111
|
16,9012
|
-35,6296
|
|
3
|
73
|
32
|
4,667
|
21,7778
|
-6,111
|
37,3457
|
-28,5185
|
|
4
|
70
|
36
|
1,667
|
2,7778
|
-2,111
|
4,4568
|
-3,5185
|
|
5
|
66
|
39
|
-2,333
|
5,4444
|
0,889
|
0,7901
|
-2,0741
|
|
6
|
63
|
42
|
-5,333
|
28,4444
|
3,889
|
15,1235
|
-20,7407
|
|
7
|
67
|
45
|
-1,333
|
1,7778
|
6,889
|
47,4568
|
-9,1852
|
|
8
|
63
|
41
|
-5,333
|
28,4444
|
2,889
|
8,3457
|
-15,4074
|
|
9
|
61
|
46
|
-7,333
|
53,7778
|
7,889
|
62,2346
|
-57,8519
|
|
Сумма
|
615
|
343
|
|
262,0000
|
|
294,8889
|
-240,3333
|
|
Среднее
|
68,333
|
38,111
|
|
|
|
|
|
В итоге при подстановке значений вычисляем ry,x1:
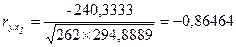
По аналогии расчета коэффициента ry,x1 вычисляем коэффициент парной корреляции ry,x2 и rx1,x2:
|
Наблюдение
|
Y(t)
|
X2(t)
|
(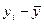 ) )
|
(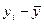 )2 )2
|
(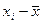 ) )
|
(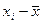 )2 )2
|
(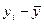 )( )(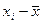 ) )
|
|
1
|
75
|
15
|
6,667
|
44,4444
|
-15,778
|
248,9383
|
-105,1852
|
|
2
|
77
|
20
|
8,667
|
75,1111
|
-10,778
|
116,1605
|
-93,4074
|
|
3
|
73
|
24
|
4,667
|
21,7778
|
-6,778
|
45,9383
|
-31,6296
|
|
4
|
70
|
30
|
1,667
|
2,7778
|
-0,778
|
0,6049
|
-1,2963
|
|
5
|
66
|
33
|
-2,333
|
5,4444
|
2,222
|
4,9383
|
-5,1852
|
|
6
|
63
|
37
|
-5,333
|
28,4444
|
6,222
|
38,7160
|
-33,1852
|
|
7
|
67
|
36
|
-1,333
|
1,7778
|
5,222
|
27,2716
|
-6,9630
|
|
8
|
63
|
40
|
-5,333
|
28,4444
|
9,222
|
85,0494
|
-49,1852
|
|
9
|
61
|
42
|
-7,333
|
53,7778
|
11,222
|
125,9383
|
-82,2963
|
|
Сумма
|
615
|
277
|
|
262,0000
|
|
693,5556
|
-408,3333
|
|
Среднее
|
68,333
|
30,778
|
|
|
|
|
|
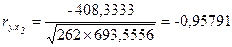
|
Наблюдение
|
X1(t)
|
X2(t)
|
(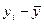 ) )
|
(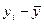 )2 )2
|
(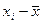 ) )
|
(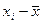 )2 )2
|
(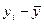 )( )(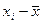 ) )
|
|
1
|
28
|
15
|
-10,111
|
102,2346
|
-15,778
|
248,9383
|
159,5309
|
|
2
|
34
|
20
|
-4,111
|
16,9012
|
-10,778
|
116,1605
|
44,3086
|
|
3
|
32
|
24
|
-6,111
|
37,3457
|
-6,778
|
45,9383
|
41,4198
|
|
4
|
36
|
30
|
-2,111
|
4,4568
|
-0,778
|
0,6049
|
1,6420
|
|
5
|
39
|
33
|
0,889
|
0,7901
|
2,222
|
4,9383
|
1,9753
|
|
6
|
42
|
37
|
3,889
|
15,1235
|
6,222
|
38,7160
|
24,1975
|
|
7
|
45
|
36
|
6,889
|
47,4568
|
5,222
|
27,2716
|
35,9753
|
|
8
|
41
|
40
|
2,889
|
8,3457
|
9,222
|
85,0494
|
26,6420
|
|
9
|
46
|
42
|
7,889
|
62,2346
|
11,222
|
125,9383
|
88,5309
|
|
Сумма
|
343
|
277
|
|
294,8889
|
|
693,5556
|
424,2222
|
|
Среднее
|
38,111
|
30,778
|
|
|
|
|
|
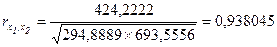
Полученные значения коэффициентов парной корреляции сведем в
следующую таблицу:
|
Y(t)
|
X1(t)
|
X2(t)
|
|
Y(t)
|
1
|
-0,86464
|
-0,95791
|
|
X1(t)
|
-0,86464
|
1
|
0,938045
|
|
X2(t)
|
-0,95791
|
0,938045
|
1
|
Из таблицы видно, что значения
коэффициентов парной корреляции указывают на весьма тесную связь переменной Y(t) с коэффициентом X2(t). Но в то же время
коэффициент rx1,x2 также имеет тесную межфакторную связь, которая
превышает тесноту связи X1(t) с Y(t). В связи с этим для улучшения
данной модели можно исключить из нее фактор X1(t) как малоинформативный, недостаточно статистически
надежный.
2) Построить линейную однопараметрическую модель регрессии Y(t)=а0+а1
X(t).
Для проведения регрессионного анализа воспользуемся EXCEL:
1) в главном меню последовательно выбираем пункты Сервис / Анализ данных;
2) в открывшемся окне Анализ
данных выбираем Инструменты анализа:
Регрессия;
3) заполняем Входной
интервал Y и Входной интервал X множеством данных Y(t) и X2(t);
4) отмечаем флажком Метки;
5) в поле Остатки отмечаем флажком Остатки, График остатков, График
подбора;
6) результат регрессионного анализа представлен в табл.
2.1-2.3;
Таблица
2.1
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
|
Y-пересечение
|
86,4539
|
2,1344
|
40,5046
|
|
X2(t)
|
-0,5888
|
0,0667
|
-8,8282
|
Во втором столбце табл.2.1
содержатся коэффициенты уравнения регрессии а0,
а1. В третьем столбце
содержатся стандартные ошибки коэффициентов уравнения регрессии, а в четвертом t-статистика, используемая
для проверки значимости коэффициентов уравнения регрессии.
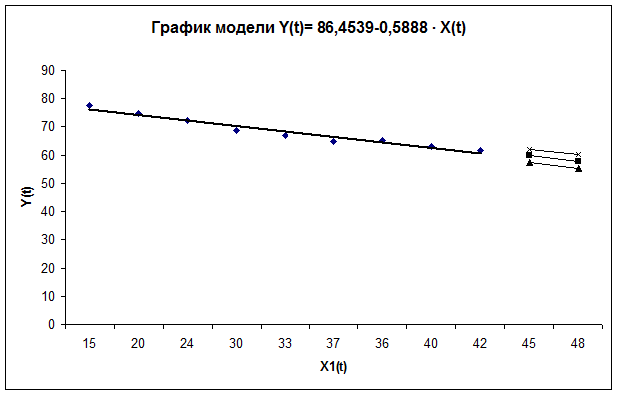
Уравнение регрессии зависимости Y(t) от X2(t) имеет
вид: Y(t)= 86,4539-0,5888 ∙ X(t)
Таблица 2.2
Расчеты по модели
регрессии
|
ВЫВОД ОСТАТКА
|
|
Наблюдение
|
Предсказанное Y(t)
|
Остатки
|
|
1
|
77,6226
|
-2,6226
|
|
2
|
74,6788
|
2,3212
|
|
3
|
72,3238
|
0,6762
|
|
4
|
68,7913
|
1,2087
|
|
5
|
67,0250
|
-1,0250
|
|
6
|
64,6700
|
-1,6700
|
|
7
|
65,2587
|
1,7413
|
|
8
|
62,9037
|
0,0963
|
|
9
|
61,7262
|
-0,7262
|
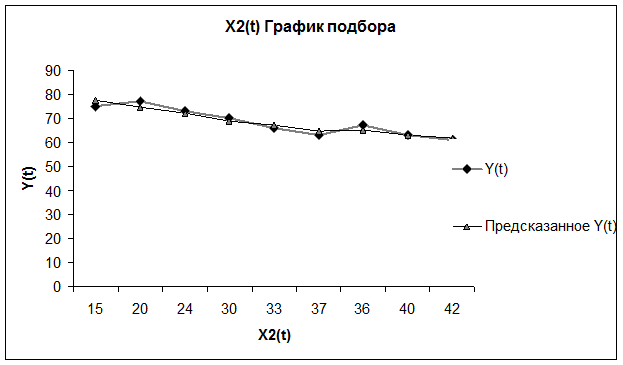
Оценка параметров
модели без ПЭВМ.
Построим линейную однопараметрическую модель регрессии для X2(t).
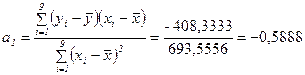
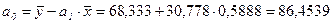
Y(t)= 86,4539-0,5888
∙ X(t).
3) Оценить качество построенной модели, исследовав ее адекватность и
точность;
Оценим
качество построенной модели, исследуя адекватность.
Модель
является адекватной, если математическое ожидание значений остаточного ряда
близко или равно нулю и если значения остаточного ряда случайны, независимы и
подчинены нормальному закону распределения.
а) при проверке независимости (отсутствия
автокорреляции) определяется отсутствие в ряду остатков систематической
составляющей (с помощью d-критерия
Дарбина-Уотсона).
Таблица 2.3
Данные для вычисления
d-критерия
|
Наблюдение
|
Y(t)
|
Y-расчетное
|
Отклонение E(t)
|
E(t)-E(t-1)
|
(E(t)-E(t-1))2
|
E(t)2
|
|
1
|
75
|
77,6226
|
-2,6226
|
|
|
6,8780
|
|
2
|
77
|
74,6788
|
2,3212
|
4,9438
|
24,4412
|
5,3880
|
|
3
|
73
|
72,3238
|
0,6762
|
-1,6450
|
2,7060
|
0,4572
|
|
4
|
70
|
68,7913
|
1,2087
|
0,5325
|
0,2836
|
1,4610
|
|
5
|
66
|
67,0250
|
-1,0250
|
-2,2337
|
4,9894
|
1,0506
|
|
6
|
63
|
64,6700
|
-1,6700
|
-0,6450
|
0,4160
|
2,7889
|
|
7
|
67
|
65,2587
|
1,7413
|
3,4113
|
11,6370
|
3,0321
|
|
8
|
63
|
62,9037
|
0,0963
|
-1,6450
|
2,7060
|
0,0093
|
|
9
|
61
|
61,7262
|
-0,7262
|
-0,8225
|
0,6765
|
0,5274
|
|
Сумма
|
|
|
|
|
47,8557
|
21,5925
|
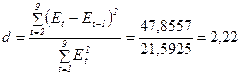 ;
; 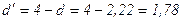
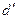 попало в интервал от d2 до 2, значит модель уровня ряда остатков
независима, автокорреляции нет, свойство независимости выполняется. Модель по
этому критерию адекватна.
попало в интервал от d2 до 2, значит модель уровня ряда остатков
независима, автокорреляции нет, свойство независимости выполняется. Модель по
этому критерию адекватна.
б) проверку
случайности уровней ряда остатков проведем на основе критерия поворотных точек.
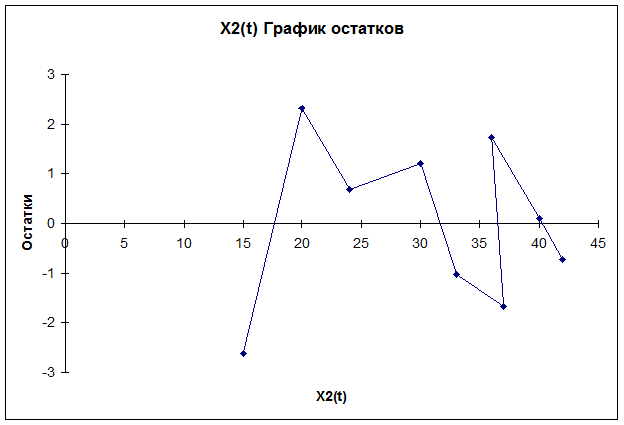
В случайном ряду чисел должно выполняться строгое
неравенство:
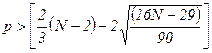 . Количество поворотных точек равно 5 (график остатков).
. Количество поворотных точек равно 5 (график остатков).
в) соответствие ряда остатков
нормальному закону распределения определим при помощи RS-критерия.
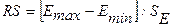 ,
,
где 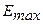 -максимальный уровень ряда остатков, равный 2,3212;
-максимальный уровень ряда остатков, равный 2,3212;
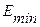 - минимальный уровень ряда остатков, равный -2,6226;
- минимальный уровень ряда остатков, равный -2,6226;
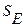 -среднеквадратическое отклонение,
-среднеквадратическое отклонение,
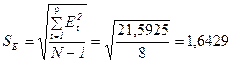 ,
,
Тогда:
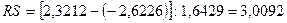
Расчетное значение попадает в
интервал (2,7…3,7), следовательно, свойство нормальности распределения
выполняется. Модель по этому критерию адекватна.
г) проверка равенства нулю
математического ожидания уровней ряда остатков осуществляется с использованием t-критерия Стьюдента.
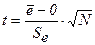 ,
,
где 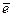 -среднее значение уровней остаточного ряда;
-среднее значение уровней остаточного ряда;
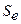 -среднеквадратическое отклонение уровней остаточного ряда.
-среднеквадратическое отклонение уровней остаточного ряда.
В нашем случае 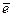 =0, поэтому гипотеза о равенстве математического ожидания
значений остаточного ряда нулю выполняется.
=0, поэтому гипотеза о равенстве математического ожидания
значений остаточного ряда нулю выполняется.
Для
расширенной характеристики модели регрессии вычислим несколько дополнительных
показателей: коэффициент детерминации R2 и
коэффициент множественной корреляции R:
|
Регрессионная
статистика
|
|
Множественный
R
|
0,9579
|
|
R-квадрат
|
0,9176
|
|
Нормированный
R-квадрат
|
0,9058
|
|
Стандартная
ошибка
|
1,7563
|
|
Наблюдения
|
9
|
Коэффициент детерминации:
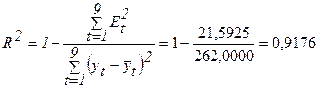
R2
показывает долю вариации результативного признака под воздействием изучаемых
факторов. Следовательно, более 91,76 % вариации зависимой переменной учтено в
модели и обусловлено влиянием включенного фактора.
R –
коэффициент множественной корреляции. R=0,9579 показывает
тесноту связи зависимой переменной Y с факторами X, включенными в модель.
4) Для модели регрессии рассчитать коэффициент эластичности и
β-коэффициент.
а) Расчет коэффициента
эластичности.
Он показывает,
на сколько процентов в среднем по совокупности изменится результат Y от своей средней величины
при изменении фактора Х на 1% от своего среднего значения:
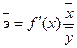
Для линейной
модели производная по функции равна коэффициенту при Х, т.е. а1.
Тогда получим:
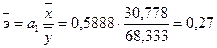
Следовательно,
при изменении Х на 1% от своего среднего значения величина Y в среднем изменится на 0,27%.
б) Расчет
β-коэффициента.
β-коэффициент
показывает, на какую часть сигмы изменяется результативный признак, при
изменении факторного признака на величину его сигмы. Сравнение
β-коэффициентов при различных факторах дает возможность оценить силу их
воздействия на результативный признак. Он вычисляется по формуле:
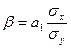 ,
,
Дисперсии
определим по формулам:
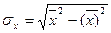 ,
,
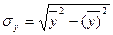
Все
необходимые вычисления сведем в таблицу:
|
Наблюдение
|
Y(t)
|
X2(t)
|
Y(t)2
|
X2(t)2
|
|
1
|
75
|
15
|
5625
|
225
|
|
2
|
77
|
20
|
5929
|
400
|
|
3
|
73
|
24
|
5329
|
576
|
|
4
|
70
|
30
|
4900
|
900
|
|
5
|
66
|
33
|
4356
|
1089
|
|
6
|
63
|
37
|
3969
|
1369
|
|
7
|
67
|
36
|
4489
|
1296
|
|
8
|
63
|
40
|
3969
|
1600
|
|
9
|
61
|
42
|
3721
|
1764
|
|
Сумма
|
615
|
277
|
42287
|
9219
|
|
Среднее
зн.
|
68,333
|
30,778
|
4698,5556
|
1024,3333
|
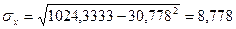 ,
,
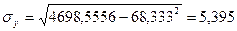
Тогда:
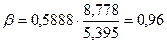 - при изменении факторного признака на величину его сигмы
результативный признак изменяется на 0,96 сигмы.
- при изменении факторного признака на величину его сигмы
результативный признак изменяется на 0,96 сигмы.
5) Построить
точечный и интервальный прогнозы на два шага вперед по модели регрессии (для
вероятности Р = 70 % используйте коэффициент v = 1,11). Прогнозные оценки фактора X(t) на два шага вперед
получить на основе среднего прироста от фактически достигнутого уровня).
Для вычисления
прогнозных оценок Y на основе построенной модели
необходимо получить прогнозные оценки фактора X.
Получим
прогнозные оценки фактора на основе величины его среднего абсолютного прироста САП.
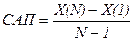 ;
;
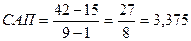 ;
;
Построим прогноз на 2 шага вперед. Для этого определим
значение X на первом и втором шагах
соответственно:
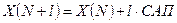 ;
;
l=1;
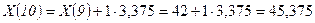 ;
;
l=2;
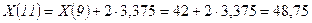 .
.
Для получения прогнозных оценок
зависимой переменной подставим в модель:
Y(t)= 86,4539-0,5888 ∙ X(t).
найденные прогнозные значения фактора X:
Y(10)= 86,4539-0,5888 ∙ X(10)= 86,4539-0,5888 ∙45,375=59,74
Y(11)= 86,4539-0,5888 ∙ X(11)= 86,4539-0,5888 ∙48,75=57,75
Определим доверительный интервал
прогноза, который будет иметь следующие границы:
- верхняя граница прогноза: Y(N+l) + U(l);
- нижняя граница прогноза: Y(N+l) – U(l).
Величина U(l) имеет вид:
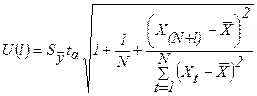 ,
,
где 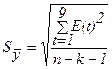 - стандартная ошибка.
Значение ошибки было определено при исследовании модели на точность и адекватность
(
- стандартная ошибка.
Значение ошибки было определено при исследовании модели на точность и адекватность
(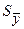 = 1,7563).
= 1,7563).
Необходимые вычисления для определения доверительного
интервала сведем в таблицу:
|
Наблюдение
|
X2(t)
|
(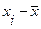 ) )
|
(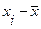 )2 )2
|
|
1
|
15
|
-15,778
|
248,9383
|
|
2
|
20
|
-10,778
|
116,1605
|
|
3
|
24
|
-6,778
|
45,9383
|
|
4
|
30
|
-0,778
|
0,6049
|
|
5
|
33
|
2,222
|
4,9383
|
|
6
|
37
|
6,222
|
38,7160
|
|
7
|
36
|
5,222
|
27,2716
|
|
8
|
40
|
9,222
|
85,0494
|
|
9
|
42
|
11,222
|
125,9383
|
|
Сумма
|
277
|
|
693,5556
|
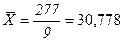
Для прогноза на два шага имеем:
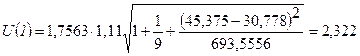
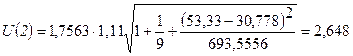
Результаты прогнозных оценок по модели регрессии представим
в таблице:
|
Время
|
Шаг
|
Прогноз
|
Нижняя граница
|
Верхняя граница
|
|
10
|
1
|
59,74
|
57,418
|
62,062
|
|
11
|
2
|
57,75
|
55,102
|
60,398
|
Отобразим на графике фактические данные, результаты расчетов
и прогнозирования.