Введение

                                                                                                          

1. Структура естественно научных знаний

 

     Естественные и гуманитарные науки.  Наука занимается изучением объективно существующих ( т.е. существующих независимо от чьего-либо сознания) объектов и явлений природы. Вопрос о том, существует ли окружающий нас мир сам по себе или он является продуктом деятельности  разума (принадлежащего некому высшему существу или каждому конкретному индивиду) составляет суть т.н. основного вопроса философии, классически формулируемом в виде дилеммы о первичности материи или сознания. В зависимости от ответа на основной вопрос философы подразделяются на материалистов (признают объективное существование окружающего нас мира, возникшего в результате саморазвития материи), объективных идеалистов (признают объективное существование мира, возникшего как результат деятельности высшего разума) и субъективных идеалистов (считают, что окружающий нас мир не существует реально, а есть плод воображения отдельного индивида) . По-видимому невозможно дать экспериментально обоснованного ответа на основной вопрос философии, хотя большинство естествоиспытателей являются приверженцами материалистических концепций.

     Все существующие научные дисциплины условно (любая классификация носит приближенный характер и неполно отражает истинную суть вещей!) разделены на две основные группы: естественнонаучные (занимаются изучением объектов природы и явлений, не являющихся продуктом деятельности человека или человечества) и гуманитарные (изучают явления объекты, возникшие как результат деятельности человека).

     Настоящий курс посвящен обзору важнейших концепций современного естествознания.

     Уровни организации материи и иерархия естественно научных знаний. Окружающие нас объекты природы имеют внутреннюю структуру, т.е. в свою очередь сами состоят из других объектов (яблоко  состоит из клеток растительной ткани, которая сложена из молекул, являющихся объединениями атомов и т.д.).  При этом естественным образом возникают различные по сложности уровни организации материи : космический, планетарный, геологический, биологический, химический, физический. Представители естественных наук, занимающиеся изучением объектов какого-либо уровня могут достичь их полного описания лишь основываясь на знаниях более “низкого” (элементарного) уровня (невозможно понять законы жизнедеятельности клетки, не изучив химизм протекающих в ней реакций). Однако реальные возможности каждого отдельного исследователя весьма ограничены (человеческой жизни недостаточно не только для того, чтобы плодотворно заниматься изучением сразу нескольких уровней, но даже заведомо не хватает на сколько-нибудь полное освоение уже накопленных знаний о каком-то одном). Из-за этого возникло деление естественно научных знаний на отдельные дисциплины, примерно соответствующие вышеперечисленным уровням организации материи: астрономию, экологию, геологию, биологию, химию и физику.  Специалисты, работающие на своем уровне, опираются на знания смежных наук, находящихся ниже по иерархической лестнице. Исключение составляет физика, находящаяся на “самом нижнем этаже” человеческих знаний (“составляющая  их фундамент”): исторически сложилось так,  что в ходе развития этой науки обнаруживались все более “элементарные” уровни организации материи (молекулярный, атомный, элементарных частиц...), изучением которых по-прежнему занимались физики.

     Естественные науки различных уровней не обособлены друг от друга. При изучении высокоорганизованных систем возникает естественная потребность в информации о составляющих их элементах, предоставляемой дисциплинами “более низких” уровней. При изучении же “элементарных” объектов весьма полезны знания о их поведении в сложных системах, где при взаимодействиях с другими элементами проявляются свойства изучаемых. Примером взаимодействия наук разных уровней может служить разработка Ньютоном классической теории тяготения (физический уровень), возникшей на основе законов движения планет Кеплера (астрономический уровень), и современные концепции эволюции Вселенной, немыслимые без учета законов гравитации.

     Естественные науки, находящиеся на нижних этажах иерархической лестницы, несомненно проще вышестоящих, поскольку занимаются более простыми объектами (строение электронного облака атома углерода, несомненно “проще пареной репы”, содержащей множество атомов с такими облаками!). Однако, именно из-за простоты изучаемых объектов науки нижних уровней сумели накопить  гораздо больше фактической информации и создать более законченные теории.

     Место математики среди естественных наук.  Обсуждавшаяся выше структура естествознания не содержит математики, без которой невозможна ни одна из современных точных наук. Это связано с тем, что сама математика не является естественной наукой в полном смысле этого понятия, поскольку не занимается изучением каких-либо объектов или явлений реального мира. В основе математики лежат аксиомы, придуманные человеком. Для математика не имеет решающего значения вопрос,  выполняются ли эти аксиомы в реальности или нет (напр. в настоящее время благополучно сосуществует несколько геометрий, основанных на несовместных друг с другом системах аксиом).

     Если математика заботит лишь логическая строгость его выводов, делаемых на основе аксиом и предшествующих теорем, естествоиспытателю важно, соответствует ли его теоретическое построение реальности. При этом в качестве критерия истинности естественнонаучных знаний выступает эксперимент, в ходе которого осуществляется проверка теоретических выводов.

     В ходе изучения свойств реальных объектов часто оказывается так, что они приближенно соответствуют аксиоматике того или иного раздела математики (напр. положение небольшого тела можно приближенно описать, задав три его координаты, совокупность которых можно рассматривать как вектор в трехмерном пространстве). При этом ранее доказанные в математике утверждения (теоремы) оказываются применимыми к таким объектам.

      Кроме сказанного, математика играет роль очень лаконичного, экономного и емкого языка, термины которого применимы к внешне совершенно разнородным объектам окружающего мира (вектором можно назвать и совокупность координат точки, и характеристику силового поля, и компонентный состав химической смести, и характеристику экономико-географического положения местности).

     Очевидно, что более простые объекты нашего мира удовлетворяют более простым системам аксиом, следствия из которых математиками изучены более полно. Поэтому естественные науки “низших” уровней оказываются более математизированными.

     Опыт развития современного естествознания показывает, что на определенном этапе развития естественно научных дисциплин неизбежно происходит их математизация, результатом которой является создание логически стройных формализованных теорий и дальнейшее ускоренное развитие дисциплины.

     Приближенный характер естественнонаучных знаний.  Несмотря на то, что естественные науки часто называют точными, практически любое конкретное утверждение в них носит приближенный характер. Причиной этого является не только несовершенство измерительных приборов, но и ряд принципиальных ограничений на точность измерений, установленных современной физикой. Кроме того, практически все реально наблюдаемые явления столь сложны и содержат такое множество процессов между взаимодействующими объектами, что их исчерпывающее описание оказывается не только технически невозможным, но и практически бессмысленным (человеческое сознание способно воспринять лишь весьма ограниченный объем информации). На практике исследуемая система сознательно упрощается путем ее замены моделью, учитывающей только самые важные элементы и процессы. По мере развития теории модели усложняются, постепенно приближаясь к реальности.

     Основные этапы развития естествознания могут быть выделены, исходя из различных соображений. По мнению автора, в качестве основного критерия следует рассматривать доминирующий среди естествоиспытателей подход к построению их теорий. При этом оказывается возможным выделение трех основных этапов.

     Естествознание древнего мира. Завершенного деления на дисциплины не существовало, создаваемые концепции в своем большинстве носили мировоззренческий характер. Экспериментальный метод познания в принципе допускался, но роль решающего критерия истинности эксперименту не отводилась. Верные наблюдения и гениальные обобщающие догадки сосуществовали с умозрительными и часто ошибочными построениями.

     Классический период развития естествознания берет свое начало с экспериментальных работ Галилея (18 век) и длится до начала нашего столетия. Характеризуется четким разделением наук на традиционные области и даже несколько гипертрофированной ролью эксперимента в их развитии (“понять- значит измерить”). Эксперимент рассматривается не только как критерий истинности, но и как основной инструмент познания. Вера в истинность экспериментально добытых результатов столь велика, что их начинают распространять на новые области и проблемы, где соответствующей проверки не производилось. При обнаружении расхождений так создаваемых концепций с реально наблюдаемыми явлениями неизбежно возникало недоумение, граничащее с попытками отрицания самой возможности познания окружающего мира.

     Современное естествознание характеризуется лавинообразным накоплением нового фактического материала и возникновением множества новых дисциплин на стыках традиционных. Резкое удорожание науки, особенно экспериментальной. Как следствие - возрастание роли теоретических исследований, направляющих работу экспериментаторов в области, где обнаружение новых явлений более вероятно. формулировка новых эвристических требований к создаваемым теориям: красоты, простоты, внутренней непротиворечивости, экспериментальной проверяемости, соответствия (преемственности). Роль эксперимента, как критерия истинности знания, сохраняется, но признается , что само понятие истинности не имеет абсолютного характера: утверждения, истинные при определенных условиях, при выходе за границы, в рамках которых проводилась экспериментальная проверка, могут оказаться приближенными и даже ложными. Современное естествознание утратило присущую классическим знаниям простоту и наглядность. Это произошло главным образом из-за того, что интересы современных исследователей из традиционных для классической науки областей переместились туда, где обычный “житейский” опыт и знания об объектах и происходящих с ними явлениях в большинстве случаев отсутствуют.

 

     Настоящий курс посвящен современным концепциям естествознания, неотделимым от знаний, накопленных в классический период развития наук. Его структура не отражает традиционного разделения знаний на отдельные дисциплины, а скорее следует историческому ходу развития основных мировоззренческих идей, берущих свое начало в наиболее фундаментальной из естественных наук - физике.

 

10. Постоянный электрический ток

     Условия возникновения тока. Электрическим током называют направленное движение заряженных частиц. Количественными характеристиками тока являются его сила тока (отношение заряда: переносимого через поперечное сечение проводника в единицу времени):

(1)  (1)       

и его плотность, определяемая соотношением:

(2)  (2)       .

Единицей измерения силы тока является ампер (1А - характерное значение тока, потребляемого бытовыми электронагревательными приборами).

      Необходимыми условиями существования тока являются наличие свободных носителей зарядов, замкнутой цепи и источника ЭДС (батареи), поддерживающего направленное движение.

     Электрический ток может существовать в различных средах: в металлах, вакууме, газах, в растворах и расплавах электролитов, в плазме, в полупроводниках, в тканях живых организмов.

      При протекании тока практически всегда происходит взаимодействие носителей зарядов с окружающей средой, сопровождающееся передачей энергии последней в виде тепла. Роль источника ЭДС как раз и состоит в компенсации тепловых потерь в цепях.

     Электрический ток в металлах обусловлен движением относительно свободных электронов через кристаллическую решетку. Причины существования свободных электронов в проводящих кристаллах может быть объяснена только на языке квантовой механики.

     Опыт показывает, что сила электрического тока, протекающего по проводнику, пропорциональна приложенной к его концам разности потенциалов (закон Ома). Постоянный для выбранного проводника  коэффициент пропорциональности между током и напряжением называют электрическим сопротивлением:

(3)    

      Сопротивление измеряют в омах (сопротивление человеческого тела составляет около 1000 Ом). Величина электрического сопротивления проводников слабо возрастает при увеличении их температуры. Это связано с тем, что при нагревании узлы кристаллической решетки усиливают хаотические тепловые колебания, что препятствует направленному  движению электронов. Во многих задачах непосредственный учет колебаний решетки оказывается весьма трудоемким. Для упрощения взаимодействия электронов с колеблющимися узлами оказывается удобным заменить их столкновениями с частицами  газа гипотетических частиц - фононов, свойства которых подбираются так, чтобы получить максимально приближенное к реальности описание и могут оказываться весьма экзотическими. Объекты такого типа весьма популярны в физике и называются квазичастицами. Помимо взаимодействий с колебаниями кристаллической решетки движению электронов в кристалле могут препятствовать дислокации - нарушения регулярности решетки. Взаимодействия с дислокациями играют определяющую роль при низких температурах, когда тепловые колебания практически отсутствуют.

     Некоторые материалы при низких температурах полностью утрачивают электрическое сопротивление, переходя в сверх проводящее состояние. Ток в таких средах может существовать без каких-либо ЭДС, поскольку потери энергии при столкновениях электронов с фононами и дислокациями отсутствуют. Создание материалов, сохраняющих сверхповодящее состояние при относительно высоких (комнатных) температурах и небольших токах является весьма важной задачей, решение которой произвело бы настоящий переворот в современной энергетике, т.к. позволило бы передавать электроэнергию на большие расстояния без тепловых потерь.

     В настоящее время электрический ток в металлах используется главным образом для превращения электрической энергии в тепловую (нагреватели, источники света) или в механическую (электродвигатели). В последнем случае электрический ток используется в качестве источника магнитных полей, взаимодействие с которыми других токов вызывает появление сил.

     Электрический ток в вакууме строго говоря невозможен из-за отсутствия в нем свободных электрических зарядов. Однако, некоторые проводящие вещества при нагревании или облучении светом способны испускать со своей поверхности электроны (термоэмиссия и фотоэмиссия), которые способны поддерживать электрический ток, двигаясь от катода к другому (положительному) электроду - аноду. При подаче на анод отрицательного напряжения ток в цепи обрывается. Описанное свойство обуславливает широкое применение электровакуумных приборов в электронных устройствах для выпрямления переменного тока. До сравнительно недавнего времени электровакуумные устройства широко использовались в качестве усилителей электрических сигналов. В настоящее время они почти полностью вытеснены полупроводниковыми приборами.

     Электрический ток в газах на первый взгляд не может существовать из-за отсутствия свободных заряженных частиц (электроны в атомах и молекулах газов прочно “связаны” с ядрами электростатическими силами). Однако, при передаче атому энергии порядка 10эВ (энергия, приобретаемая свободным электроном при прохождении через разность потенциалов в 10 В), последний переходит в ионизированное состояние (электрон уходит от ядра на сколь угодно большое расстояние). В газах при комнатных температурах всегда присутствует очень небольшое количество ионизированных атомов, возникших под действием космического излучения (фотоионизация). При помещении такого газа в электрическое поле заряженные частицы начинают разгоняться, передавая нейтральным атомам набранную кинетическую энергия и ионизуя их. В результате развивается лавинообразный процесс нарастания числа свободных электронов и ионов - возникает электрический разряд. Характерное свечение разряда связано с выделением энергии при рекомбинации электронов и положительных ионов. Типы электрических разрядов весьма разнообразны и сильно завися от состава газа и внешних условий.

      Плазма. Вещество, содержащее смесь нейтральных атомов, свободных электронов и положительных ионов, называют плазмой. Плазма, возникающая в результате сравнительно слаботочных  электрических разрядов (напр. в трубках “дневного света”) характеризуется весьма малыми концентрациями заряженных частиц по сравнению с нейтральными  (). Обычно ее называют низкотемпературной, поскольку температура атомов и ионов близка к комнатной. Средняя же энергия гораздо более легких электронов оказывается гораздо большей. Т.о. низкотемпературная плазма является существенно неравновесной, открытой средой. Как отмечалось, в подобных средах возможны процессы самоорганизации. Хорошо известным примером является генерация в плазме газовых лазеров высоко упорядоченного когерентного излучения.

     Плазма может так же может быть термодинамически равновесной. Для ее существования необходима очень высокая температура (при которой энергия теплового движения сравнима с энергией ионизации). Такие температуры существуют на поверхности Солнца, могут возникать при очень мощных электрических разрядах (молнии), при ядерных взрывах. Такую плазму называют горячей.

      Атмосферное электричество. Земля является достаточно хорошим проводником электрического тока (по сравнению с сухим воздухом). На высоте около 50 км ионизирующее космическое излучение обуславливает наличие  ионосферы - слоя сильно ионизированного газа. Измерения показывают, что между ионосферой и поверхностью Земли существует огромная разность потенциалов (около 5000000 В), причем ионосфера имеет положительный по отношению к Замле заряд. Наличие разности потенциалов между Землей и “небом” приводит к появлению тока очень малой плотности (A/) даже в таком плохом проводнике как воздух. Полный ток, приходящий на поверхность планеты, весьма велик (ок. А), а выделяемая им мощность сравнима с мощностью всех построенных электростанций (  Вт). Возникают естественные вопросы о механизме поддержания указанной разности потенциалов и о причинах, по которым ее наличие до сих пор никак не используется человеком.

     В настоящее время установлено, что основным механизмом, заряжающим “небо” относительно Земли являются грозы. Капли воды и кристаллы льда, перемещаясь вниз к основанию грозовой тучи собирают на себе имеющиеся в атмосфере отрицательные заряды и тем самым заряжают нижнюю часть грозового облака отрицательным электричеством до потенциалов, во много раз превосходящих потенциал Земли. В результате между Землей и тучей возникает очень большое электрическое поле, направленное в противоположную сторону по сравнению с полем, существующем в безоблачную погоду. Вблизи выступающих с поверхности Земли проводящих предметов это поле еще усиливается и оказывается достаточным для ионизации газа, которая нарастает по лавинообразному закону. В результате возникает очень мощный электрический разряд, называемый молнией. Вопреки бытующему мнению, молния начинается на Земле и бьет в тучу, а не наоборот.

      Характерное для ясной погоды электрическое поле напряженностью 100В/м не удается не только использовать, но даже ощутить, хотя на равной росту человека высоте при его отсутствии оно создает разность потенциалов около 200В. Причиной этого является низкая проводимость воздуха и, как следствие, малые плотности текущих на поверхность Земли токов. Введение в электрическую цепь хорошего проводника (человека), шунтирующего двухметровый воздушный столб, практически не изменяет суммарного сопротивления цепи “небо-Земля”, ток в которой остается неизменным. Вызываемое им падение напряжения на теле человека составляет около U=IR=0.2мкВ, что лежит значительно ниже порога чувствительности нашего организма.

     Электрический ток в живых тканях. Важная роль электрических импульсов для жизнедеятельности организмов предполагалась еще более 200 лет назад. Сейчас известно, что  эти импульсы используются для обеспечения управления работой органов и передачи информации между ними в процессе жизнедеятельности. Роль кабелей для передачи сигналов в сложнейшем “биологическом компьютере” играют нервы, основу которых составляют узко специализированные клетки - нейроны. Основные функции этих клеток - прием, обработка и усиление электрических сигналов. Нейроны связываются друг с другом в “сеть” при помощи специальных удлиненных выростов - аксонов, выполняющих функции проводников.  Исследования распространения электрических сигналов в аксонах выполнялись совместно биологами, химиками и физиками в 30-60 годах нашего века и явились одним из первых удачных примеров  плодотворного сотрудничества представителей смежных естественных наук.

    Как оказалось, свойства электрических импульсов, распространяющихся в аксонах существенно отличаются от привычных для электротехники: 1) скорость распространения импульсов по аксону оказывается на несколько порядков меньше характерных для металлических; 2) после прохождения электрического импульса существует “мертвое” время, в течение которого распространение следующего импульса невозможно; 3) существует пороговое значение напряжения (импульсы с амплитудой ниже пороговой не распространяются); 4) при медленном нарастании напряжения даже до превышающего порог значения импульс по аксону не передается (“аккомодация”).

     Перечисленные нехарактерные для традиционной электротехники особенности проводимости аксонов  нашли объяснения в рамках весьма специфического электро-химического механизма, центральная роль в котором принадлежит полу проницаемой для ионов клеточной мембране, отделяющей содержащий аномально высокую концентрацию ионов K+ и низкую - Na+  внутренний объем клетки (и ее аксона) от окружающей среды, заполненной физиологическим раствором. В результате хаотического теплового движения частиц через границу между областями с различными концентрациями положительных ионов возникают диффузионные потоки (K+ - из клетки, Na+ - внутрь ее), скорости которых регулируются проницаемостью клеточной мембраны и электрической разностью потенциалов по обе стороны от нее. Изменения проницаемости  мембраны для каждого из ионов приводит к изменению количества заряженных частиц, пересекающих границу и, следовательно, к изменению электрического потенциала аксона относительно внешней среды. Как показали опыты, проводимость участка мембраны изменяется в зависимости от приложенной к нему разности потенциалов. Т.о. подаваемый на участок аксона электрический импульс изменяет на небольшое время (зависящее от свойств аксона) проводимость мембраны, что ведет к перераспределению зарядов, усилению импульса и формированию его заднего фронта. При этом аксон одновременно играет роль проводника и “усиливающих подстанций - ретрансляторов”, что позволяет избежать затухания сигналов, передаваемых в организме на достаточно большие расстояния.

     Интересно, что весьма сходную проблему с той, что была решена природой, незадолго до раскрытия механизма проводимости аксона пришлось решать в радиотехнике при попытке организовать транс Атлантическую кабельную связь. Для того, чтобы избежать затухания и искажения сигнала в длинной линии, кабель пришлось разделить на сравнительно короткие звенья, между которыми были помещены усилители. Опыт, накопленный физиками при создании длинных линий кабельной связи существенно облегчил решение проблемы о механизме электропроводности аксона.

 

11. Классическая электродинамика

      История развития классической электродинамики является поучительным примером того, как  математизация естественно научной дисциплины и переход к изящному (хотя и достаточно сложному) языку описания  повлекли за собой качественный скачок в понимании целого ряда явлений природы, часть из которых была первоначально предсказана теоретически  (“на кончике пера”), а потом получила блестящее экспериментальное подтверждение.  В настоящей теме будет содержаться достаточно большое количество математических формул, приводимых лишь с целью иллюстрации красоты и компактности языка математики.

     Непрерывные распределения зарядов. Входящие в выражения для электростатических и магнитостатических полей (9_4) и (9_8) суммы в случае макроскопических заряженных тел содержат очень большое число слагаемых, соответствующих вкладам в поля от точечных зарядов. Их вычисление неудобно с чисто “технической” точки зрения: математическая операция суммирования более трудоемка, чем, например, интегрирование (сказанное относится  к аналитическим расчетам, при компьютерном счете суммирование предпочтительнее взятия интегралов,  однако в 19 веке подобной альтернативы в математике не существовало). Переход к интегрированию требовал приближенной замены дискретного распределения элементарных зарядов на непрерывное, характеризуемое плотностью электрического заряда 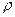  (отношение величины заряда к объему содержащего его небольшого, но макроскопического элемента пространства):

(1)      .

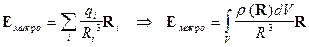 Естественно, что  замена (1) приводила к  “сглаживанию” рассчитываемых макроскопических полей по сравнению с реальными микроскопическими, сильно изменяющимися на сравнимых с размером атома расстояниях. Описанный переход к непрерывному распределение зарядов существенно упрощал расчеты, не снижая их практическую  ценность (наука и техника 19 века еще не доросли до эффектов, происходящих на микроскопическом уровне организации материи).

     Математический формализм. Переход к непрерывным распределениям зарядов и токов позволил переписать законы электро и магнитостатики сразу в нескольких математических формах, эквивалентных по физическому смыслу, но существенно различающихся по технике выполнения конкретных расчетов:

интегральные формулировки:

(2)  (2)        ;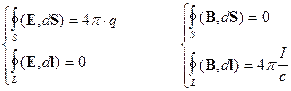

дифференциальные формулировки:

(3)     ;

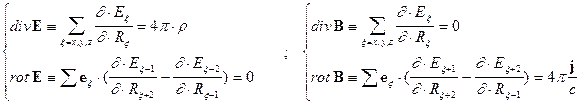расчет полей через скалярный 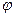 и векторный  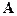потенциалы:

(4)  (4)     .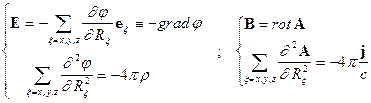

Т.о. адекватное описание одних и тех же законов естествознания возможно на различных языках математики.

     Операторы. В начале 20 века в математике были введены новые объекты - операторы, без использования которых современная физика была бы немыслима. Понятие оператора является естественным обобщением традиционного для классической математики понятия функции. Если под функцией понимается закон (правило, отображение), по которому одному числу (набору чисел) ставится в соответствие другое число (набор чисел), то под оператором подразумевают закон, по которому одному объекту (группе объектов) ставится в соответствие другой объект (группа). Наиболее часто встречаются операторы, действующие на функции (операторы умножения на число, дифференцирования, интегрирования и т.д.) или векторы (оператор поворота, проектирования и т.д.). Весьма полезной оказалась идея определения математических операций над операторами. Например, под произведением двух операторов подразумевается оператор, выполняющий последовательно действия каждого из перемножаемых операторов. Для операции умножения операторов в общем случае не выполняется свойство коммутативности:

(5)     .

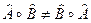    Использование языка операторов существенно сокращает запись многих математических формул и делает их более “элегантными”.  Так введение лишь одного дифференциального оператора “набла”

(6)  (6)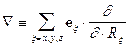      

при помощи стандартным образом определенных операций скалярного ( , )  и векторного [ , ] умножения позволяет записать системы уравнений (3) и (4) в весьма компактной форме:

(3’)           ;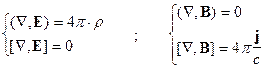

(4’)    ,                    .

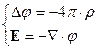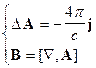В последних равенствах использован оператор Лапласа:

(7)     .

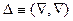Помимо краткости записи преимущество операторного метода состоит в том, что. с самим оператором набла можно обращаться почти так же, как с обычным вектором, что, несомненно, облегчает громоздкие выкладки.

     Закон электромагнитной индукции Фарадея. Долгое время электрические и магнитные явления считались независимыми, хотя даже на уровне магнитостатики это не совсем верно: магнитостатическое поле порождается постоянными токами, существование которых в веществе невозможно без наличия электрического поля. Фарадей экспериментальным путем установил, что изменяющееся во времени магнитное поле может порождать электрическое. Это электрическое поле в отличие от порождаемого зарядами потенциального электростатического является вихревым, т.е. его линии представляют собой замкнутые кривые (рис. 11_1). Открытый Фарадеем закон индукции впоследствии имел колоссальное практическое значение, поскольку открыл весьма удобный и дешевый способ преобразования механической энергии движения источников магнитного поля в электрическую, ныне лежащий в основе промышленного производства электроэнергии.

     С точки зрения математической записи уравнений для поля открытое Фарадеем явление требует видоизменения системы уравнений (6):

(10)      .

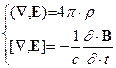     Гипотеза Максвелла.   Рассмотрев совместно систему уравнений (7) и (10) Максвелл обратил внимание на следующие ее недостатки:

1. Указанная система несовместна с законом сохранения заряда.

2. Система оказалась весьма несимметричной даже для случая описания электромагнитного поля в пустом пространстве (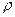=0 и j=0).

     Несоответствие уравнений закону сохранения заряда было достаточным аргументом для того, чтобы усомниться в их истинности, поскольку законы сохранения носят весьма общий характер. Оказалось, что существует множество способов видоизменения системы уравнений (7), (10), приводящих их в соответствие с законом сохранения. Максвеллом был выбран простейший из возможных путь, приводящий систему к симметричному виду в случае ее использования для описания полей в пустом пространстве. В последнее уравнение было добавлено слагаемое, описывающее возможность генерации вихревого магнитного поля изменяющимся электрическим (“ток смещения”):

(11)                        .

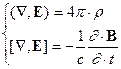
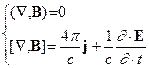     Чисто математическими следствиями из видоизмененной системы уравнений Максвелла были утверждение о сохранении энергии в электромагнитных процессах и теоретический вывод о возможности независимого от зарядов и токов существования поля в виде электромагнитных волн в пустом пространстве. Это последнее предсказание нашло блестящее экспериментальное подтверждение в знаменитых опытах Герца и Попова, положивших основу современной радиосвязи. Рассчитываемая из системы  (11) скорость распространения электромагнитных волн оказалась равной экспериментально измеренной скорости распространения света в вакууме, что означало объединение практически ранее независимых разделов физики электромагнетизма и оптики в одну законченную теорию.

     Проблема существования магнитного монополя. Колоссальный успех теории Максвелла продемонстрировал возможность теоретического поиска новых законов природы на основе анализа математических уравнений, описывающих ранее известные закономерности, с обязательной экспериментальной проверкой таким образом “угадываемых” результатов.

     Симметричная для описания электромагнитных полей в пустом пространстве система уравнений Максвелла (11) существенно “теряет свою красоту”  при учете электрических зарядов и токов: создаваемое электрическими зарядами потенциальное поле Е не имеет аналога в магнитных взаимодействиях. Эта ассиметрия послужила поводом для постановки множества экспериментов по поиску магнитных монополей (или магнитных зарядов) - гипотетических частиц, являющихся источником потенциального магнитного поля и теоретических исследований их предполагаемых свойств. До настоящего времени надежных экспериментальных данных о существовании магнитных монополей не получено.

     Противоречия между электродинамикой и классической физикой. Сформулированные в виде законченной теории и выдержавшие экспериментальную проверку законы электромагнетизма Максвелла оказались в противоречии с принципами, лежащими в основе классического миропонимания Галлилея - Ньютона:

1. Удовлетворяющие принципу относительности Галилея классические силы могут зависеть от времени, расстояний между телами и их относительных скоростей, т.е. величин, не изменяющихся при переходе из одной инерциальной системы отсчета в другую. Магнитостатические поля и связанные с ними силы Лоренца являются функциями скоростей зарядов по отношению к наблюдателю и различны в разных инерциальных системах отсчета. Т.о. явления природы, обусловленные электромагнитными взаимодействиями, с точки зрения классической физики в различных инерциальных системах отсчета должны протекать по-разному.

2. Получаемая в результате решения уравнений Максвелла скорость распространения электромагнитных волн в пустом пространстве оказалась независящей от скоростей движения как источника этих волн, так и наблюдателя. Этот вывод полностью противоречило классическому закону сложения скоростей.

    Все попытки видоизменить уравнения электромагнетизма так, чтобы привести их в согласие с принципами классического естествознания приводили к теоретическому предсказанию эффектов, ненаблюдаемых на эксперименте, и были признаны несостоятельными.

     Преобразования Лоренца.  Поскольку уравнения Максвелла не были инвариантными относительно преобразований Галилея, т.е. вопреки требованиям принципа относительности изменяли свою форму при переходе из одной инерциальной системы отсчета в другую, по правилам, задаваемым соотношениями:

(12)        ,

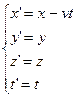Лоренцем был поставлен естественный вопрос об отыскании таких преобразований координат и времени, которые не изменяли бы уравнений Максвелла и были при этом максимально простыми. Эта задача была им решена как чисто математическая:

(13)        .

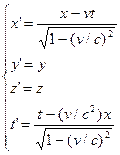Сравнивая преобразования Галилея (12) и Лоренца (13), легко заметить, что последние переходят в классические в случае скоростей, малых по сравнению со скоростью света с. Т.о. предложенные Лоренцем соотношения удовлетворяли принципу соответствия, согласно которому новая теория должна согласовываться со старой о областях, где последняя была надежно проверена на экспериментах. Кроме того, следующий из преобразований Лоренца релятивистский закон сложения скоростей оставлял скорость света инвариантной относительно переходя в любую инерциальную систему отсчета, движущуюся со скоростью, меньшей с.

     Опыты Майкельсона. Следующее из уравнений Максвелла утверждение о постоянстве скорости света при переходах в другие системы отсчета полностью противоречило классическим представлениям. Вставал естественный вопрос о его экспериментальной проверке. Весьма изящный эксперимент был осуществлен Майкельсоном с помощью специально сконструированного им прибора - интерферомета, позволяющего сравнивать времена распространения световых  сигналов вдоль двух взаимно перпендикулярных отрезков прямых, ограниченных на концах зеркалами (рис. 11_2). Идея опыта состояла в попытке зарегистрировать различие  скоростей распространения света вдоль разных плеч интерферометра,  вызванное орбитальным движением Земли. Опыты с интерферометром Майкельсона дали отрицательные результаты: скорость света с высокой точностью  оказалась независящей от соотношения направлений его распространения и движения Земли.

     Многочисленные попытки спасти классический закон сложения скоростей путем введения гипотетической среды - эфира, в которой распространяются  световые колебания потерпели полную неудачу свойства предполагаемой Среды оказывались весьма экзотическими, никаких экспериментальных подтверждений ее реального существования получено не было.

     Выход из возникшей на рубеже веков в естествознании тупиковой ситуации был предложен А. Эйнштейном, создавшим специальную теорию относительности (СТО), в которой на основе двух хорошо проверенных на эксперименте постулатов (утверждений) строится внутренне непротиворечивая (хотя и весьма странная с точки зрения классического естествознания и житейского опыта) концепция, объясняющая преобразования Лоренца и предсказывающая ряд новых явлений, реально зарегистрированных в природе.

 

12.  Основные положения Специальной теории относительности

     Постулаты Эйнштейна. Современный релятивистский подход к описанию природных явлений базируется на двух постулатах Эйнштейна.

    Первый является естественным обобщением принципа относительности Галлилея с механических на все без исключения явления природы и может быть сформулирован как утверждение о невозможности наблюдателю, находящемуся в замкнутой системе отсчета, при помощи какого-либо физического (а значит и любого другого) опыта установить, покоится ли его система отсчета или находится в состоянии равномерного прямолинейного движения. В пользу этого постулата свидетельствует обширный житейский опыт, показывающий, что находящийся в закрытом помещении (трюме корабля)  наблюдатель не в состоянии зарегистрировать факт его движения не только в результате постановки механических опытов, но и с помощью своих ощущений, в основе возникновения которых лежат, как известно, электрохимические процессы.

      Вторым постулатом Эйнштейна является утверждение о постоянстве скорости света, неоднократно проверявшееся не только Майкельсоном, но и впоследствии в более точных экспериментах.

       Основные выводы релятивистской кинематики.  На основе сформулированных постулатов Эйнштейна пересматриваются все основные положения классической кинематики. Делается вывод о том, что понятия одновременности собитий, доительностьи временного промежутка и длины отрезка перестают носить абсолютный характер, становясь зависимыми от выбора системы отсчета, из которой ведется наблюдение (подобно тому, как при классическом описании координаты материальной точки и ее скорость носили относительный характер).

     Предсказываемый релятивистской теорией эффект замедления времени состоит в том, что с точки зрения движущегося относительно рассматриваемой системы наблюдателя все интервалы времени (t’), характеризующие поцессы в этой системе (колебания маятников часов, распад нестабильных частиц,  старение биологических организмов и т.д.) увеличиваются по сравнению с интервалами, наблюдаемыми в самой этой системе ():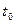

(1)       .

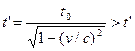Для находящихся же в самой расматриваемой системе наблюдателей происходящие в ней процессы протекают совершенно нормально, а время у движущегося наблюдателя “течет замедленно”.

     Эффект сокращения расстояний состоит в уменьшении длин отрезков с точки зрения наблюдателей, перемещающихся вдоль этих отрезков (отрезки, ориентированные перпендикулярно скорости относительного движения сохраняют свою длину неизменной):

(2)    

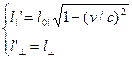
     Описанные эффекты проявляются лишь при скоростях, сравнимых со скоростью света и в настоящее время экспериментально зарегистрированы в пучках ультарелятивискских частиц, создаваемых на современных ускорителях. Например, короткоживущие частицы (время жизни 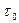, двигаясь с околосветовыми скоростями, вопреки классическим представлениям достигают приемника, удаленного на расстояние, значительно превышающее 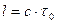. С точки зрения неподвижного наблюдателя это явление можно объеснить эффектом замедления времени (1), “удлинняющим” жизнь частицы, с точки зрения наблюдателя, движущегося вместе с частицей - эффектом сокращения расстояния до мишени, “летящей ему навстречу” (2).

     Полученные Лоренцем преобразования (10.13) являются чисто математическим следствием рассмотренных соотношений (1) и (2).

     С эффектом замедления времени часто ошибочно связывают “парадокс близнецов” - утверждение о том, что двигавшийся с околосветовыми скоростями космический путешественник  должен вернуться  на Землю менее постаревшим, чем его брат, оставшийся дома. Кажущийся парадокс связан с тем, что всилу относительности равномерного движения с точки зрения космического путешественника эффект замедления времени должен наблюдаться на самой Земле. Реального противоречия не возникает, поскольку для того, чтобы возвратиться домой, космонавт должен в течение определенного времени двигаться с ускорением (тормозить, разворачивать корабль, вновь ускоряться), что нарушает симметрию между ним и наблюдателем на Земле (напомним, что ускорение носит абсолютный характер). Адекватное описание явлений, происходящих в ускоренно движущихся системах отсчета, выходит за рамки СТО и состаяляет предмет). Общей Теории Относительности (ОТО) .

     Пространство Минковского. Широко используемая в классической физике векторная форма записи законов природы объясняется не только желанием сэкономить место, но и является математическим отражением факта инвариантности законов природы относительно поворотов выбранной системы координат в пространстве, что, разумеется, требует инвариантной формы их математической записи. Действительно, в изображенных на рис. 12_1 повернутых друг относительно друга системах координат проекции всех векторов на одноименные оси различны, но равенство

(3)    

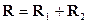
справедливо в каждой из систем, т.е. остается инвариантным относительно пространственных вращений. Помимо равенств между векторами инвариантами являются скалярные произведения векторов и вычисляемые с их помощью квадраты длин:

(4)     .

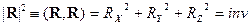Координаты же вектора в новой системе отсчета могут быть рассчитаны через координаты в старой с помощью тригонометрии:

(5)       .

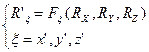      Последовательное релятивистское описание явлений природы должно быть инвариантным относительно переходов из одной инерциальной системы отсчета в другую, движущуюся относительно первой. Как отмечалось, при таких переходах перестает быть справедливым классический векторный закон сложения скоростей, длина векторов изменяется, а в закон преобразований их компонент (преобразования Лоренца) помимо пространственных переменных входит время:

(6)        .

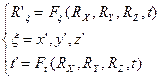      В создавшейся ситуации естественным выходом был переход от несвязанных друг с другом пространственного (трехмерного) и временного (одномерного) описаний явлений к  единому  описанию событий в четырехмерном пространстве-времени (пространстве Минковского)  при помощи четырехвекторов, три компоненты которых совпадают с обыконвенными простарнственными, а последняя дает временное описание. В этом пространстве переход в движущуюся систему отсчета рассматриваентся как обобщение понятия поворота, аналогом трехмерных траекторий являются четырехмерные кривые - мировые линии, инвариантами являются скалярные произведения четырехвекторо, определяемые соотношением:

(7)      ,

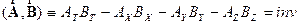и интервалы, являющиеся аналогами длин векторов:

(8)     

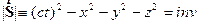
(следствие преобразований Лоренца).

отличающимся знаками от обычного “трехмерного”  определения. В связи с этим геометрическое свойства псевдоевклидового пространства Минковского существенно отличаются от привычных  свойств евклидового пространства . 

    Световой конус.Мировыми линиями свтовых лучей, выходящих из одной точки пространства Минковского (т.е. одновременно испущенных из одной точки трехмероного пространства) являются прямые, составляющие с осью ct одинаковый угол 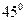 и образующие световой конус (рис. 12_2).. Мировые линии всех тел могут лежать лишь внутри светового конуса, поскольку допустимые скорости движения не могут превосходить с. Лежащие в верхней части светового конуса точки пространства Минковского образуют абсолютное будущее (множество событий, на которые в принципе можно повлиять, находясь в вершине конуса), нижняя часть светового конуса соответствует абсолютному прошлому (множество событий, которые в могли повлиять на происходящее в вершине конуса). Вне светового конуса лежат абсолютно недоступные событмя (т.е. невлияющие и независимые от происходящего в вершине конуса).

     Релятивистская динамика строится как обобщение классической в соответствии с требованиями релятивистской инвариантности. Важнейшую роль в ней играет четырехвектор энергии-импульса, получающийся из четырехвектора скорости домножением на инвариант массу покоя (массу тела в системе отсчета, где оно покоится):

(9)    

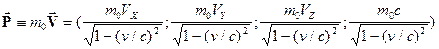
Пространственные компоненты этого четырехвектора весьма схожи с классическим импульсом mV. Учитывая эту аналогию иногда вводят понятие релятивистской массы, величина которой возрастает с увеличением скорости движения тела относительно неблюдателя:

(10)     .

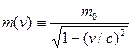С учетом (10) релятивистское уравнение движения в привычных трехмерных обозначениях принимает вид, аналогичный второму закону Ньютона в импульсной формулировке:

(11)    

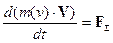
Возрастание релятивистской массы является одним из оснований утверждения о невозможность разогнать тело с ненулевой массой покоя до скорости света: по мере увеличения его скорости под действием постоянной силы ускорение начнет уменьшаться и стремиться к нулю при .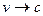

     Эффект возрастания релятивистской массы при приближении скорости к предельной наблюдается экспериментально в ускорителях ультарелятивистских частиц сиххрофазотронов, принцип действия которых аналогичен циклотронным ускорителям. Основное отличие состоит в том, что при больших скоростях разгоняемых частиц радиусы их орбит

(12)    

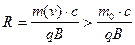
и периоды вращения

(13)    

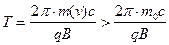
начинают существенно превосходить результаты расчетов по классическим формулам. Т.о. в настоящее время результаты СТО используются не только в науке, но и в инженерных расчетах.

     Смысл четвертой компоненты четырехвектора энергии-импульса можно установить на основе сравнения ее произведения на скорость света с классическим выражением для кинетической энергии:

(12)    

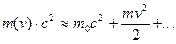
Принцип соответствия позволяет предположить, что величина

(13)    

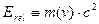
представляет собой релятивистское выражение для энергии тела, связанной с его движением. Однико, даже в случае нулевой скорости, согласно (13) лубое толо обладает энергией покоя, пропорциональной его массе. Эта колоссальная (по сравненью с характерными для классической теории масштабами) энергия до создания теории относительности оставалось “незамеченной” из-за того, что в подавляющем большинстве процессов суммарная масса составляющих систему объектов остается практически неизменной. Открытие энергии покоя имело громадное значение для развития энергетики и военной техники.

     Релятивистская электродинамика. Создание релятивистской теории позволило переписать систему уравнений Максвелла в весьма элегантной и краткой четырехмерной форме:

(14)     ,

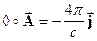где

(15)      

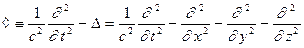
- релятивистски инвариантный четырехмерный аналог оператора Лапласа - оператор Д’Аламбера,

(16)     -

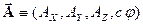-четырехмерный потенциал, состоящий из трех компонент векторного потенциала магнитного поля и скалярного потенциала электрического, 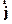 - четырехвектор плотности тока, получающийся домножением четырехвектора скорости на релятивистски-инвариантную величину электрического заряда.

      Излучение электромагнитных волн. Решением Уравнения (14) в пустом пространстве являются электромагнитные волны, распространяющиеся в пустом пространстве с инвариантной относительно преобразований Лоренца скоростью с. Рассмотрение уравнения (14) с учетом зарядо и токов приводит к выводу, что электромагнитные волны создаются электрическими зарядами при их ускоренном движении. При этом электромагнитное поле, создаваемое точечным зарядом на больших расстояниях от него (рис. 12_3) имеет вид

(17)      ,

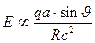т.е. убывает гораздо медленнее, чем статические поля. Это свойство обуславливает удобство использования переменных электромагнитных полей в целях связи.

     Происхождение силы Лоренца. Существование зависящей (вопреки требованием классической теории) от скорости относительно наблюдателя магнитной силы Лоренца в релятивистской теории находит весьма “неожиданное” объяснение. Сами магнитные взаимодействия и описывающая их сила являются “лишними” в теории электричества, т.е. адекватное описание реальности возможно и бех их использования на основе закона Кулона и релятивистских формул преобразования физических величин при переходах из одной системы отсчета в другую. Релятивистских эффект изменения силы взаимодействия между двумя зарядами с точки зрения движущегося наблюдателя был замечен экспериментально задолго до создания теории относительности и отнесен за счет существования “новой” магнитной силы, которую пришлось наделить весьма странными свойствами. Если бы теория магнетизма создавалась в наши дни, “магнитные взаимодейстивя” были бы предсказаны теоретически как релятивистская поправка к  электростатическим.

 8.  Неравновесные ансамбли. Открытые системы. Самоорганизация

        Проблема необратимости в статистической физике. Существование необратимых процессов в макро мире не вызывает сомнения. К ним относится установление равновесной температуры при тепловом контакте горячих и холодных тел, перемешивание первоначально разделенных газов в результате диффузии и многие другие. С точки зрения молекулярно-кинетической теории, сводящей тепловые макроскопические процессы к механическим взаимодействиям на микроскопическом уровне, возникновение необратимости достаточно неожиданно, поскольку механические явления обратимы во времени. Формально ето следует из того, что во второй закон Ньютона входит вторая производная по времени (ускорение), не меняющее знак при операции обращения времени t -> -t. В частности это, например,  означает, что заснятое при большом увеличении на кинопленку столкновение и разлет двух молекул будет быглядеть на экране вполне правдоподобно, независимо от того, как пленка вставлена в проэктор. Если же на пленку снят процесс диффузии газов (например окрашенных в разные цвета) так, что молекулы не различимы, а система наблюдается вцелом, выбор правильного направления движения пленки не вызывет сомнений.

     Проблема понимания механизма возниконовения необратимости имеет большое философское значение. Наличие необратимых процессов определяет направленность течения времени. В мире, где существуют только обратимые процессы, по-видимому было бы невозможно отличить прошлое от будущего.

       Макроскопические и микроскопические состояния. Энтропия. Механизм возникновения необратимости легко понять на примере расчета интуитивно весьма маловероятного явления: образования вакуума в одной половине комнаты вследствие случайного перемещения всех хаотически движущихся молекул в другую половину. Очевидно, что вероятность нахождения одной молекулы в выбранной половине объема равна 0,5.  Если движения молекул независимы, то вероятность всем N молекулам оказаться в этой половине равна произведению вероятностей для каждой из молекул. Т.о. полный вакуум в половине комнаты возникает с вероятностью

(1)       .

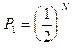О том, насколько мала эта величина, можно говорить, срввнив ее с вероятностью повседневно-наблюдаемого явления - равномерного распределения газа в двух половинах комнаты. Если мысленно занумеровать все молекулы, то вероятность обнаружения всех первых  N/2 молекул в одной половине объема равна

(2)        

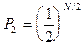
и совпадает с вероятностью найти все осавшиеся молекулы во второй половине. Полная вероятность описанного равномерного распределения, очевидно равна квадрату (2) и совпадает с (1).

     Полученный “странный” результат не означает того, что в комнате легко задохнуться. Ошибка расчета состоит в том, что для дыхания человека несущественно, какие именно молекулы кислорода находятся в его половине комнаты: если какую-либо пару молекул, находящихся в разных частях объема, поменять местами, этого “никто не заметит”. Таким образом, вероятность равномероного распределения молекул между двумя половинами объема превосходит вероятность образования вакуума в одной из половин в огромное число раз, равное количеству всевозможных перестановок молекул между этими половинами.

  Приведенный пример позволяет сформулировать общий механизм возникновения необратимых макроскопических процессов. Различные макроскопические состояния могут реализовываться различным числом отличающихся друг от друга микроскопических, переход между которыми не приводит к новым макро состояниям. Наиболее вероятными являются те макроскопические состояния, которым соответствует наибольшее число микроскопических. Такие состояния и являются термодинамически равновесными. Если же искусственно создать неравновесное  макроскопическое состояние, реализуемое малым числом микроскопических, вероятность их повтроной реализации оказывается весьма малой, что и означает переход системы в макроскопическое состояние, соответствующее термодинамическому равновесию. Самопроизвольный выход макроскопической системы из состояния термодинамического равновесия возможен, но крайне маловероятен.

     Количественной мерой вероятности реализации макроскопического состояния является его энтропия,  определяемая соотношением

(3)        ,

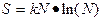
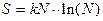где N - число соответствующих ему микроскопических состояний. Очевидно, что в ходе необратимых процессов (т.е. при переходе к более вероятным состояниям) энтропия системы возрастает, а при обратимых переходах - сохраняется. Закон возрастания энтропии носит не строгий, а вероятностный характер. Иногда говорят, что энтропия является мерой беспорядка в системе.

      Вечный двигатель второго рода представляет собой гипотетическое устройство, предназначенное для совершения макроскопической работы за счет энергии теплового движения вещества. Функционирование подобного устройства в замкнутой системе не противоречит закону сохранения энергии, но крайне маловероятно, поскольку позволило бы осуществить процесс, сопровождающийся уменбшением энтропии (теплый газ, находящийся в сосоянии термодинамического равновесия, с помощию такого “двигателя” можно было бы немного остудить, а полученную за счет этого энергию использовать на нагревание части газа, что вывело бы его из равновесия).

     Остроумный пример  неосуществимого вечного двигателя второго рода был предложен Максвеллом (“демон Максвелла”).  Его основу составлял замкнутый объем с перегородкой, небольшое отверстие в которой перекрывалось дверцей, управляемой сидящим внутри демоном так, что в одну сторону пропускались только быстро летящие молекулы, а в другую - медленные. В результате работы такого “демона” в замкнутой системе произошло бы разделение газа на холодный и горячий, т.е. возникло бы неравновесное состояние. Невозможность подобной работы “демона” объясняется тем, что будучи изолированным от окружающей среды, он, стремясь к термодинамическому равновесию с газом в сосуде, неизбежно нагреется до его температуры, начнет сам совершать хаотические тепловые колебания и, следовательно, потеряет способность отличать “быстрые” молекулы от “медленных”.

          Тепловая смерть Вселенной. Наш мир можно рассматривать как гигантскую термодинамическую систему, находящуюся в неравновесном состоянии (энергия сконцентрирована главным образом в горячих звездах и постепенно мигрирует в гораздо более холодное межзвездное пространство). Все имеющиеся двигатели (к которым вполне могут быть отнесены и биологические объекты) оказываются работоспособными в конечном итоге за счет существования указанной глобальной неравновесности. Естественными являются вопросы о причинах ее возникновения и перспективах, связанных со стремлением глобальной системы к термодинамическому равновесию.

      Возникновение глобальной неравновесности обычно связывают со случайной флюктуацией, имеющей гигантские масштабы и, поэтому, крайне маловероятной. Проблема малой вероятности частично снимается антропогенным принципом (до тех пор, пока флюктуация не возникла, некому было ее ожидать и задумываться над тем, насколько это будет маловероятным событием). После возникновения неравновесности стали возможными необратимые процессы, т.е. возникло понятия времени. Роль такого “начала отсчета мирового времени”  обычно приписывается большому взрыву исчерпывающее описании которого лежит далеко за рамками классического описания природы.

      Предполагаемое конечное равновесное состояние принято называть тепловой смертью Вселенной. Если весь окружающий мир действительно можно считать замкнутой системой, к которой применимы выводы классической термодинамики, при достижении равновесия он должен представлять собой однородный “бульон” с постоянной температурой, плотностью вещества и излучения, в котором не будет возможным никакое направленное преобразование энергии.

13. Ядерные реакции и современная энергетика

         Неядерные источники энергии. Вся промышленная энергетика на нашей планете до конца 40х годов в качестве источника в конечном итоге использовала энергию, поставляемую Солнцем. Гидро электростанции работают за счет энергии спускающейся с гор к морю воды, которая “доставляется” обратно за счет процессов испарения с поверхности океана. Используемые в тепловых двигателях горючие вещества (дерево, уголь, нефть) имеют биологическое происхождение и возникли в результате утилизации энергии Солнца растениями в процессе фотосинтеза. Ветряные двигатели используют энергию циркуляции атмосферы, возникающей из-за ее неоднородного нагрева. Исключение составляют пожалуй только приливные электростанции, не получившие до сих пор широкого распространения.

      Учитывая определяющую роль Солнца в современной энергетике, представляется важным рассмотреть процессы, обеспечивающие функционирование нашей звезды и возможности их использования для производства энергии в земных условиях.

     Сильные ядерные взаимодействия. В настоящее время надежно установлено, что составляющие вещество атомы представляют собой положительны ядра, окруженные отрицательно заряженными  электронными облаками. В свою очередь ядра состоят из тяжелых частиц нуклонов:

 положительных протонов и незаряженных нейтронов. Для обозначения причин, удерживающих находящиеся в ядре положительные частицы от разлетания из-за электрического отталкивания были введены сильные ядерные взаимодействия. Ядерные силы существенно превосходят электрические лишь на расстояниях, сравнимых с размерами ядра, и очень быстро ослабевают при удалении нуклонов друг от друга (поэтому такие силы называют близко действующими). Механизм возникновения ядерных сил до сих пор окончательно не выяснен, хотя их свойства хорошо изучены экспериментально и находят практическое применение.

     Дефект массы. Энергия связи. При сближении нуклонов на расстояния, допускающие “включение” ядерных сил, они образуют связанную систему с энергией, меньшей энергии свободных частиц. Неизбежное при таком процессе выделение энергии 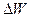согласно формуле Эйнштейна (12_13) приводит к уменьшению массы системы по сравнению с массой свободных частиц на величину

(1)     ,

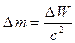называемую дефектом массы. Измерения масс ядер позволяют определить энергию связи, выделяющуюся при образовании ядер (рис,  13_1). Убывание энергии связи в области тяжелых ядер объясняется возрастанием их геометрических размеров, приводящим к уменьшению ядерных сил притяжения между удаленными друг от друга нуклонами по сравнению с силами их электрического отталкивания.

     Из энергетических соображений ясно, что легкие ядра должны стремиться к соединению в более тяжелые (реакции ядерного синтеза), а тяжелые ядра - к распаду на более легкие части (реакции деления ). Соответствующие находящимся в средней части таблицы Менделеева химическим элементам ядра обладают максимальной энергией связи и поэтому стабильны.

     Исторически ядерная реакция деления в земных условиях была осуществлена раньше, чем реакция синтеза.

     Цепная реакция деления ядер урана. В природе помимо широко распространенного стабильного изотопа урана 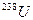 в малых количествах существуют ядра изотопа 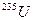, способных к спонтанному (самопроизвольному) делению на две примерно равные части, сопровождающемуся вылетом двух нейтронов:

(2)      .

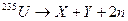Каждый из образовавшихся нейтронов может быть поглощен 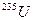, что вызывает вынужденное деление изотопа

(3)      ,

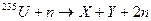приводящее к дальнейшему увеличению числа нейтронов. Т.о. возникают предпосылки возникновения лавинообразно нарастающей цепной реакции деления, сопровождающейся громадным выделением энергии в виде ускоряемых силами электрического отталкивания кусков ядер урана. В природе такой процесс обычно не неблюдается из-за того, что превосходящие по концентрации способный к делению изотоп ядра 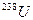 эффективно поглощают нейтроны без последующего деления. Исключение, по-видимому, составляют лишь реакции деления тяжелых ядер, происходящие в недрах некоторых планет (в том числе и Земли).

     Для искусственного осуществления цепной реакции (3) соединения урана обогащают, удаляя из них изотопы 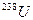. Обогащение урана - весьма сложная и дорогостоящая операция, поскольку оба изотопа имеют одинаковые химические свойства и не могут быть разделены стандартными методами. При объединении нескольких небольших объемов обогащенного урана в один, масса которого превышает критическую, потери вылетающих из образца нейтронов уменьшаются, что приводит к возникновению цепной реакции, носящей характер весьма мощного взрыва, сопровождающегося выделением большого количества энергии, возникающей вследствие уменьшения массы участвующих в реакции частиц.

     Ядерные реакторы. С точки зрения энергетики представляет интерес осуществление управляемой реакции деления, протекающей при стационарной концентрации нейтронов. В принципе она может быть осуществлена путем введения в активную зону реактора с надкритической массой веществ, поглощающих нейтроны (реакторы на быстрых нейтронах). большее распространение получили более легко осуществимые и относительно менее опасные реакторы на медленных нейтронах, в основе которых лежат эффекты резкого увеличения вероятности реакции (3) в случае малых скоростей нейтронов и потери способности к их поглощению у изотопа 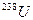. Реактор на медленных нейтронах представляют собой совокупность стержней из слабо обогащенного урана и замедлителя (вещества, способного эффективно уменьшать скорость образовавшихся при делении быстрых нейтронов, но не поглощающего их). Вылетающие из урановых стержней нейтроны отдают свою энергию замедлителю и попадают в другой стержень уже с малой скоростью, при которой из поглощение невозможно, а реакция вынужденного деления - весьма вероятна. 

     Стационарный режим работы реактора не является устойчивым и невозможен без внешнего управления. Управление  процессами в реакторе осуществляется за счет механических перемещений поглотителей нейтронов, возможные скорости которых намного меньше характерных скоростей рождения нейтронов в реакции (3). Управление оказывается возможным благодаря существованию значительно более медленного процесса рождения запаздывающих нейтронов , обусловленных слабыми ядерными взаимодействиями.

Выделяющаяся в реакторе тепловая энергия передается жидкому охладителю и впоследствии преобразуется в тепловую, электрическую или механическую форму.

     Несомненным преимуществом атомных электростанций является высокая энергетическая эффективность уранового топлива (отношение энергоотдачи к массе вещества), что приводит к значительному удешевлению его транспортировки и, следовательно, производимой энергии. К недостаткам использования ядерных реакторов в интересах энергетики следует отнести прежде всего экологическую опасность их топлива и продуктов, возникающих после деления, обусловленную их радиоактивностью. Так проблема утилизации отходов ядерного горючего и демонтажа отработавших запланированный срок ядерных котлов до сих пор не решена.

     Термоядерный синтез. Для осуществления реакции синтеза достаточно сблизить нуклоны на расстояние, достаточное для “включения” ядерных сил притяжения. Этому препятствуют электрические силы отталкивания, приводящие к возникновению потенциального барьера реакции (рис. 13_2), для преодоления которого нуклонам необходимо сообщить весьма значительную кинетическую энергию. В земных условиях температуру, обеспечивающую “поджигание” термоядерной реакции, удается получить за счет цепной реакции деления урана . “Водородная бомба”  представляет собой объем с ядерным горючим (обычно дейтерий), помещенный внутрь урановой бомбы, играющей роль запала, поджигающего реакции ядерного синтеза:

(4)    

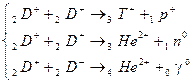
     Реакции термоядерного синтеза по-видимому являются источником, поддерживающим горения звезд. В пользу этого говорят данные астрономических наблюдений о химическим составе звезд (в основном легкие элементы - водород, гелий, являющиеся сырьем для реакций синтеза) и из температуре (температура Солнца 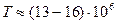K достаточна для поддержания реакций водородного цикла:

(5)       .

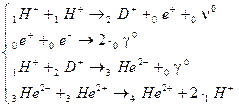     При более высоких температурах начинается “горение” ядер более тяжелых элементов(реакции гелиевого, углеродного, аргонового циклов), которое происходит с меньшим по сравнению с (5) энерговыделением, но играет решающую роль в процессах синтеза ядер тяжелых элементов нашей Вселенной.

     Исходная для водородного цикла (5) реакция превращения водорода в дейтерий протекает весьма медленно, т.к. входящий в нее процесс распада протона на нейтрон и позитрон обусловлен не сильными, а слабыми ядерными взаимодействиями. О реальном протекании такой реакции модно судить по наличию возникающих в ее результате легких частиц - нейтрино. Эксперименты по регистрации приходящего с Солнца нейтринного потока весьма сложны (нейтрино слабо взаимодействуют с веществом и пролетают сквозь него, “не оставляя следа”; помимо “солнечных” нейтрино имеется сильный фон, создаваемый прилетающими из дальнего космоса частицами) и до сих пор дают отрицательные результаты. Отсутствие приходящих с солнца нейтрино можно либо отнести к ошибкам в весьма сложном эксперименте,  либо рассматривать как указание на протекание на солнце отличных от (5) реакций, либо как свидетельство о том, что реакции горения водорода на нашей звезде уже прекратились, а ее свечение - есть результат эффекта пленения излучения в плотной горячей плазме.

     Проблема управляемого термоядерного синтеза. Главной проблемой в  осуществлении коммерческого производства энергии за счет реакции синтеза состоит в удержании горячей плазмы, в ограниченном объеме реактора: при ее контакте со стенками атомы последних разрушаются. На звездах проблема удержания “решается” весьма просто: сильное гравитационное поле не дает плазме покинуть зону реакции. В условиях Земли, очевидно, такой способ удержания неосуществим.

     В течение нескольких десятилетий проблему удержания пытаются решить, заменяя гравитационные силы более мощными - магнитными. Плазма помещается в неоднородное магнитное поле (“магнитные бутылки”), где заряженные частицы совершают квази периодическое движение между областями сгущения линий (аналогично тому, как космические частицы движется между магнитными полюсами Земли). Другой, более распространенной конфигурацией плазменного шнура в магнитном поле является тор (“Пристонский бублик”). Описанные устройства токамаки до сих пор не оказались работоспособными из-за разрушения конфигурации удерживающего магнитного поля дополнительными полями, генерируемыми сильными токами в плазме.

     Другой подход к решению проблемы получил название лазерного термоядерного синтеза и состоит в облучении интенсивном дейтериевой мишени лазерным излучением, вызывающем частичное испарение ее поверхность, сжатие и, как следствие, разогрев до около солнечных температур. Основные сложности связаны с наличием принципиальных ограничений на предельную мощность лазеров, их низким КПД, проблемой фокусировки на небольшой мишени и синхронизации срабатывания нескольких лазеров.

     В последние годы обсуждаются возможности осуществления термоядерного синтеза в значительно более “мягких” (по сравнению с горячей плазмой) условиях за счет процессов ядерного катализа. убедительных экспериментальных данных о возможности реализации такого подхода пока не получено.

     Реализация управляемой реакции термоядерного синтеза явилась бы настоящим переворотом в современной энергетике, поскольку запасов дейтерия, содержащегося в 1км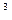океанской воды в принципе достаточно для  обеспечения сегодняшних энергетических потребностей человечества  в течение 1 года ( при этом практически вся вода, оставшаяся после извлечения ничтожной примеси “тяжелой составляющей” может быть возвращена в океан.

 

14. Гравитация и геометрические свойства пространства

     Весьма слабые гравитационные силы на современном этапе развития Вселенной играют определяющую роль в процессах космического масштаба, где электромагнитные взаимодействия оказываются в значительной степени скомпенсированными за счет существования равного количества разноименных зарядов, а коротко действующие ядерные силы проявляются только областях сосредоточения плотного и горячего вещества. Современное понимание механизма возникновения гравитационных сил стало возможным лишь после создания Теории Относительности, т.е. почти через три столетия после открытия Ньютонам закона Всемирного тяготения.

     Силы инерции.  Созданию современной теории гравитации предшествовало осознание глубокой связи, существующей между силами тяготения и псевдосилами инерции. Последние с классической точки зрения не являются мерой реального взаимодействия между телами, а вводятся в неинерциальных системах отсчета чисто формально для обеспечения возможности записи в них уравнений движения, совпадающих по форме со Вторым законом Ньютона. Так все пассажиры внутри равноускоренно движущегося автобуса относительно связанной с ним неинерциальной системы отсчета “летят к стенке” с одинаковым ускорением (равным ускорению автобуса), оставаясь “на самом деле” неподвижными относительно “хорошей” инерциальной системы отсчета, связанной с Землей. Для объяснения этого явления с точки зрения находящегося в автобусе наблюдателя приходится предположить, что при ускорении на все объекты действуют силы инерции, пропорциональные их массе и приводящие к одинаковым ускорениям:

(1)      .

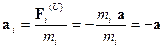     При вращательном движении неинерциальных систем отсчета выражение для силы инерции приобретет более сложный вид (в частности появляется слагаемое, зависящее от скорости движения тела - Криолисова сила наличие которой “объясняет” асимметрию размывания берегов рек, текущих в перпендикулярном вращению Земли направлении и вращение плоскости колебаний  маятника Фуко).

     Особенности гравитационных сил. Принцип эквивалентности. Сформулированный И.Ньютоном  закон гравитации по форме весьма схож с законом Кулона:

(2)       ,

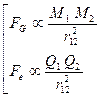что позволяет по аналогии с электрическим зарядом ввести гравитационный заряд (или гравитационную массу) - меру способности тел участвовать в гравитационных взаимодействиях. Гравитационная масса оказывается строго пропорциональной массе инертной (вводимой как коэффициент пропорциональности между силой и ускорением во втором законе Ньютона). Именно эта пропорциональность позволила измерять гравитационные заряды в тех же единицах, что и инертную массу (коэффициент пропорциональности “спрятан” в гравитационную постоянную).

     Пропорциональность гравитационной силы инертной массе делает ее весьма схожей с силой инерции. В частности при поступательном  движении неинерциальной системы отсчета с ускорением, равным ускорению свободного падения, вдоль направления гравитационных сил наступает полная компенсация сил тяготения и инерции - явление невесомости. Помещенный в закрытый лифт наблюдатель, ощущая исчезновение веса не может решить, что произошло в действительности: либо лифт начал падать вниз с ускорением свободного падения, либо исчезло гравитационное поле Земли.

     Обобщая описанный мысленный эксперимент А.Эйнштейн пришел к формулировке принципа эквивалентности: никаким опытом наблюдатель, помещенный в замкнутую систему отсчета не может установить, движется ли эта система отсчета с ускорением в пустом пространстве или покоится во внешнем гравитационном поле.

     Принцип эквивалентности в значительной степени устраняет “выделенность” инерциальных систем отсчета и позволяет исключить из теории само понятие гравитационных взаимодействий, факт наличия или отсутствия которых установить опытным путем, вообще говоря, оказывается невозможным. Наблюдаемые же на опыте отклонения траектории тел, перемещающихся вблизи массивных объектов трактуются не как результат взаимодействия, а как следствие искривления пространства.

     Искривленное пространство обладает геометрическими свойствами, существенно отличающимися от евклидового. В математическом формализме понятие кривизны пространства тесно связано с видом матрицы его метрического тензора - совокупности чисел 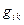, входящих в обобщенное определение скалярного произведения векторов:

(4)      .

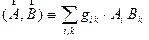Обычно эту совокупность записывают в виде таблицы (матрицы) размерами 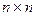(где n - размерность пространства):

(5)       .

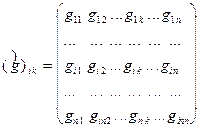В частных случаях трехмерного евклидового пространства и четырехмерного псевдоевклидового пространства Минковского метрические тензоры имеют вид:

(6)     ;

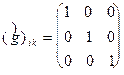
(7)       ,

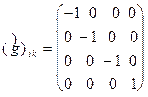т.е. представляющие их матрицы  диагональны.  Такие пространства являются неискривленными. 

     Если же матрица метрического тензора пространства содержит недиагональные элементы, пространство оказывается искривленными. Например, метрический тензор двумерного искривленного пространства - поверхности сферы имеет вид:

(7)         .

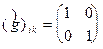     Основные идеи Общей Теории Относительности. Исходя из разработанной им Специальной Теории Относительности А.Эйнштейн сделал вывод о том, что помещенный в неинерциальную систему отсчета наблюдатель должен зарегистрировать наличие искривления пространства. Действительно, находящийся на вращающемся диске наблюдатель, измеряющий отношение длины окружности к радиусу, получит число, отличное от 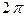, поскольку с точки зрения покоящегося наблюдателя  эталон длины будет изменять свои размеры при поворотах относительно обусловленной вращением диска скорости (рис. 14_1).

     Учитывая аналогию возникающих в неинерциальных системах отсчета сил инерции с гравитационными, А.Эйнштейн предположил, что массивные тела вызывают вокруг себя локальное искривление четырехмерного пространства-времени:

(8)     .

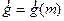     Обобщением закона инерции Галилея на случай искривленных пространств является утверждение о том, что мировыми линиями свободных тел являются геодезические (кривые, соответствующие минимальному собственному времени движения между заданными двумя точками). Движение вдоль геодезической в искривленном пространстве с точки зрения трехмерного наблюдателя  воспринимается  как движение по трехмерной кривой с переменной скоростью, что  в рамках классического подхода “объясняется” действием гравитационных сил.

     Уравнений гравитации в Общей Теории Относительности являются нелинейными:  при наличии больших масс  принцип суперпозиции нарушается.

     Экспериментальное подтверждение ОТО. Релятивистская теория гравитации удовлетворяет принципу соответствия ( в пределе малых масс и скоростей из нее непосредственно выводится закон Всемирного тяготения Ньютона ).  В то же время уравнения гравитации предсказывают ряд наблюдаемых эффектов, необъяснимых с позиций классической физики:

1. Прецессия эллиптических орбит планет, движущихся в поле сферических тел (зарегистрирована у ближайшей к Солнцу планеты - Меркурия).

2.   Эффект “абсолютного” замедления времени в гравитационном поле или при ускоренном движении (зарегистрирован по измерению времени распада нестабильных ядер и “красному смещению” световых волн в гравитационном поле).

3.   Искривление лучей света вблизи массивных тел, отличное по величине от эффекта, предсказываемого классической теории (наблюдается по изменению видимого положения звезд вблизи края Солнца).

      Одним из наиболее веских аргументов в пользу правильности ОТО является ее внутренняя логичность, красота и элегантность.

     Проблемы создания Общей Теории Поля.  После создания ОТО возникла весьма заманчивая перспектива  построит единое описание всех взаимодействий в природе, объяснив их соответствующими искривлениями пространства (“Общая Теория Поля”). А.Эйнштейн не смог реализовать эту программу, потерпели неудачи и многочисленные попытки его последователей. С сегодняшней точки зрения возможность построения такой теории в рамках чисто Эйнштейновского подхода представляется проблематичной, поскольку в построении теории электромагнитных взаимодействий был сделан весьма крупный шаг, заключающийся в создании квантовой механики, основополагающие идеи которой выходят далеко за рамки Теории относительности.

     Создание Теории Относительности было первым шагом в построении современной концепции естествознания. Ее роль состояла не только в уточнении и обобщении классических формул: было показано, что знания об окружающем мире не носят абсолютного характера и могут претерпевать существенные уточнения и изменения в ходе развития науки.  Описывающая реально наблюдаемые явления природы теория может базироваться на утверждениях и идеях, не всегда согласующихся с общепринятым мнением и “здравым смыслом”, являющимся обобщением повседневного опыта.

 

 

15.  Строение и эволюция Вселенной

     Космологические модели Вселенной. Поскольку гравитационные взаимодействия являются доминирующими на мега-уровне организации материи, космологические модели Вселенной должны строится в соответствии с требованиями Теории Относительности на основе реально наблюдаемых астрофизических явлений:

1. Однородность и изотропности космического пространства.

2. Конечная интенсивность светового потока, приходящего из космоса.

3. Красное смещение в спектрах излучения далеких звезд.

4. Существование реликтового излучения (однородного и изотропного фона электромагнитных волн, соответствующего температуре ок. 3К).

     Конечное количество света, приходящего от звездного неба, заставляет отвергнуть классические представления о бесконечном космическом пространстве, однородно заполненным звездами. Предпринимаемые в рамках классической концепции попытки построения космологических моделей с неоднородным распределением звезд в пространстве находятся в противоречии с астрономическими наблюдениями (неоднородность в концентрации звезд наблюдаются только на “относительно малых”  космических масштабах вплоть до межгалактических скоплений).

     А.Эйнштейном была предложена модель Вселенной, в которой локальные искривления пространства-времени гравитирующими массами приводит к глобальному искривлению, делающему Вселенную замкнутой по пространственным координатам. В этой цилиндрической модели Эйнштейна временная координата не искривляется (время равномерно течет от прошлого к будущему).  Впоследствии цилиндрическая модель была усовершенствована голландским астрофизиком Виллем де Ситтером, предположившим на основании наблюдаемого красного смещения, что время в удаленных частях Вселенной течет замедленно (искривление по временной координате) - модель замкнутой гиперсферы.. Обе эти стационарные модели Вселенной имеют два недостатка: необходимость предположить существование дополнительных зваимодействий, препятствующих сжатию Вселенной под действием гравитирующих масс, проблема “утилизации” света, испущенного звездами в предшествующие моменты времени в замкнутое пространство.

     На сегодняшний день наиболее популярна предложенная Фридманом модель расширяющейся Вселенной  (красное смещение и конечная светимость неба объясняются эффектом Доплера, нет необходимость во введении компенсирующих гравитацию взаимодействий), глобально искривленной из-за наличия гравитирующих масс. Обсуждаются ее две модификации:

1. Замкнутая модель (геометрический аналог - расширяющаяся гипресфера) предсказывает постепенное замедление расширения вследствие тормодения гравитационными силами с последующим переходом к сжатию.

2, Открытая модель (геометрический аналог -”седло”) замедляющееся расширение, происходящее бесконечно долго.

      В настоящее время предпочтение отдается открытой модели, поскольку оценки средней плотности вещества во Вселенной, сделанные на основе наблюдаемой концентрации звезд, показывают, что гравитационные силы не способны остановить происходящее с наблюдаемой скоростью разбегание. Оценки могут существенно измениться в пользу закрытой модели при наличии в космосе скрытых масс несветящегося вещества (например за счет ненулевой массы покоя нейтрино).

     Уравнения Общей Теории Относительности оказались весьма “гибкими” и допускают наличие большого числа космологических моделей Вселеной и сценариев их временного развития.

     Проблема Большого Взрыва. Наличие разбегания галактик в настоящее время требует предположения о том, что в прошлом вещество Вселенной было более плотным. Экстраполяция наблюдаемых скоростей на значительно более ранние периоды позволяет ценить время, когда это расширение началось (из точки???) в результате Большого Взрыва - ок. 25 млд.лет назад. Известные на сегодняшний день законы физики позволяют воспроизвести достаточно правдоподобный сценарий расширения, начиная с нескольких тысячных секунды после Большого Взрыва (что происходило до этого, напр. предшествовало ли ему сжатие предыдущего цикла, на современном этапе развития естествознания не обсуждается, поскольку не может быть хотя бы косвенно проверено на эксперименте).

     Горячая Вселенная. В первые моменты температура вселенной была столь высока, что в ней могли существовать лишь самые легкие элементарные частицы: фотоны, нейтрино и т.д. Быстрое расширение горячего сжатого “газа” вело к его охлаждению. Уже на первых секундах расширения стало возможным образование электронов и протонов, существующих в виде горячей плазмы и сильно взаимодействующих друг с другом и излучением, на долю которого приходилась основная доля энергии во Вселенной. Т.о. на ранней стадии, длящейся около 1 млн. лет во вселенной преобладали электромагнитные и ядерные  взаимодействия.

     Спустя указанный срок температура упала до величины, допускающей рекомбинацию электронов с протонами в нейтральные атомы водорода. С этого момента взаимодействие излучения с веществом практически прекратилось, доминирующая роль перешла к гравитации. Возникшее на стадии горячей Вселенной и постепенной остывающее в результате ее расширения излучение дошло до нас в виде реликтового фона.

     Холодная Вселенная.  На последующей стадии “холодной” Вселенной на фоне продолжающегося расширения и остывания вещества стали возникать гравитационные неустойчивости:  за счет флуктуаций плотности водородного газа стали возникать зоны его уплотнения, притягивающие к себе газ из соседних областей и еще больше усиливающие собственное гравитационное поле. Самоорганизация вещества во Вселенной (сложная неравновесная система, описываемая нелинейными уравнениями гравитации) в конечном итоге привела к возникновению крупномасштабной квазиупорядоченной межгалактической ячеестой структуры, а ее дальнейшая фрагментация дала начало быдущим галактикам и звездам. Анализ деталей этого процесса возможен на основании весьма сложных уравнений гирдро-газодинамики - теории нестационарного движения вещества и до сих пор удовлетворительно не разработан. Достаточно ясно, что в результате гравитационного сжатия выделяющаяся энергия в конечном итоге приводила к вторичному разогреву водородного топлива до температур, достаточных для начала термоядерных реакций водородного цикла.

     Эволюция звезд.  Первая стадия жизни звезды подобна солнечной - в ней доминируют реакции водородного цикла. Тампература звезды определяется ее массой и степенью гравитационного сжатия, которому противостоит главным образом световое давление. Звезда образует относительно устойчивую колебательную систему, ее периодические слабые сжатия и расширения определяют звездные циклы. По мере выгорания водорода в центре звезды, ее гелиевое ядро остывает, а зона протекания реакции синтеза перемещается на переферию. звезда “разбухает”, поглащая планеты ее системы, и остывает, превращаясь в красного гиганта.

     Дальнейшее сжатие гелиевого ядра поднимает его температуру до зажигания реакций гелиевого цикла. Водородная оболочка постепенно рассеивается, образуя звездную туманность, а сильно сжатое ядро раскаляется до высоких температур, соответствующих свечению бело-голубым светом (“белый карлик”). по мере выгорания топлива звезда угасает, превращаясь в устойчивого “черного карлика” - характерный итог эволюции большинства звезд с массой, порядка солнечной.

     Более массивные звезды (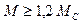) на этапе превращения в белого карлика теряют водородную оболочку в результате мощного взрыва, сопровождающегося многократным увеличением светимости (“сверх-новые звезды”). После выгорания их ядер сил давления в плазме оказывается недостаточным для компенсации гравитационных сил. В результате уплотнения вещества электроны “вдавливаются” в протоны с образованием нейтральных частиц. Возникает нейтронная звезда - весьма компактное (радиус в несколько километров) и массивное образование, вращающееся с фантастически высокой для космических объектов скоростью: около одного оборота в секунду. Вращающееся вместе со звездой его магнитное поле посылает в пространство узконаправленный луч электромагнитного (часто- рентгеновского) излучения, действуя подобно маяку. Источники мощного периодического излучения, открытые в радиоастрономии, получили название пульсаров.

     Звезды с массой, превосходящей массу Солнца более, чем в два раза, обладают столь сильным гравитационным полем, что на стадии нейтронной звезды их сжатие на останавливается. В результате дальнейшего неограниченного сжатия - гравитационного коллапса звезда уменьшается до таких размеров, что скорость, необходимая для ухода тела с ее поверхности на бесконечность превышает предельную (скорость света). При этом ни одно тело (даже свет) не может покинут непрерывно сжимающуюся звезду, представляющую собой “черную дыру”, размерами всего в несколько колометров. Существование черных дыр допускают уравнения Общей Теории Относительности.  В области черной дыры пространство-время сильно деформированы.

     Астрономические наблюдения затруднены, поскольку такие объекты не излучают свет. Однако обнаружены звезды, совершающие движение, характерное для компонент двойных звезд, хотя парной звезды не наблюдается. Весьма вероятно, что ее роль играет черная дыра или не излучающая нейтронная звезда.

     Помипо перечисленных обнаружен ряд астрофизических объектов, свойства которых не укладываются в приведенные схемы - квазары. Наблюдаемое их излучение аналогично пульсарному, но очень сильно смещено в красную область. Величина красного смещения указывает на то, что квазары находятся так далеко, что их наблюдаемая яркость соответствует излучению, превосходящему по интенсивности излучения галактического скопления. В то же время наличие быстрых изменений интенсивности ставит вопрос о механизме согласования излучения элементами системы, размеры которой должны составлять тысячи световых лет.

 

                                        Раздел  -  3

МИР  ГЛАЗАМИ  НИЛЬСА  БОРА                           

16.  Волны и их восприятие

     Волны и частицы в классическом естествознании. Вещество в классической теории обычно рассматривается как совокупность дискретных неделимых частиц - материальных точек. В зависимости от рассматриваемой задачи в их роли могут выступать макроскопические объекты, молекулы, атомы и т.д.

     Введение в естествознание концепции поля, в большинстве случаев описываемого непрерывными и обращающимися на бесконечности в 0 весьма сложными функциями координат и времени 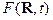, ставит вопрос о их разложении по более простым “базисным” функциям, с которыми легче производить расчеты. Такое представление функций аналогично процедуре нахождения проекций вектора на выбранные оси координат. Основное отличие состоит в том, что в случае “обычных“ векторов число ортогональных координатных осей и соответствующих им базисных векторов (размерность пространства) весьма ограничено (в евклидовом пространстве их 3), пространство же непрерывных функций оказывается бесконечно мерным, число элементов его базиса часто оказывается даже несчетным. В качестве базисных могут выбираться различные наборы функций. В большинстве задач наиболее удобны гармонические: синусы и косинусы. Теорема о разложении в ряды и интегралы Фурье утверждает, что любая достаточно гладкая функция может быть представлена как суперпозиция (сумма или интеграл) гармонических функций с различными частотами.

     В случае зависящей только от времени исходной функции 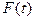 о ее Фурье разложении  говорят как о  представлении в виде суммы гармонических колебаний различных частот 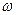, каждое из которых имеет вид

(1)      .

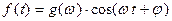В природе встречается множество процессов, представляющих собой почти гармонические колебания (напр. изменение электрического поля в конденсаторе, включенном в цепь колебательного контура - рис. 16_1 , широко используемого в качестве маятника в электронных часах). По существу все системы, имеющие точки устойчивого равновесия, могут совершать гармонические колебания вблизи этих точек.

     Если рассматриваемая функция зависит только от пространственных координат 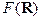, она может быть представлена суммой пространственных гармоник вида:

(2)       .

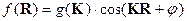     В общем случае функций, зависящих и от координат и от времени, их можно представить в виде суммы плоских монохроматических волн, каждая из которых описывается математическим выражением вида:

(3)      .

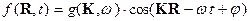     На рис. 16_2 изображены такие волны в одномерном и двухмерном случаях. Помимо плоских волн иногда используют разложения на сферические, цилиндрические и др. монохроматические волны. В качестве примера на рис. 16_3 приведена “мгновенная фотография” круговых (двухмерных сферических) волн. Примерами объектов природы, приближенно описываемых отдельными плоскими монохроматическими волнами, являются волны на поверхности моря (без “гребешков”), звуковые волны от камертона, излучение лазера.

     Т.о. монохроматические волны, как и точечные частицы, являются не столько понятиями, отражающими свойства реально существующих объектов, сколько моделями, существенно облегчающими математическое рассмотрение явлений природы. Наличие ряда объектов и явлений, приближенно описываемых этими моделями, привело к их некоторой абсолютизации на классическом этапе развития естествознания.

 

       Математический формализм описания волн и частиц.  Функцию, описывающую плоскую монохроматическую волну (3), удобно записывать с использованием многомерных обозначений в комплексном виде

(4)     ,

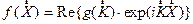причем знак операции взятия вещественной части комплексного числа обычно для краткости опускается.

     Для описания распределения плотностей (массы, заряда, спина и т.д.) точечных объектов вводят так называемые дельта-функции , математические свойства которых весьма экзотичны:

(5)       ,

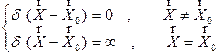причем на бесконечность функция уходит так “далеко”, что объем под ее графиком оказывается равным конечной величине - 1. Рис. 16_4  дает представление о виде дельта-функции.

 

     Аналогия между разложением вектора по базису и Фурье-представлением функций.  Ортонормированный базис  (совокупности взаимно ортогональных векторов единичной длины) {e} определяется соотношением:

(6)      ,

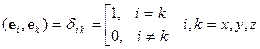Любой вектор R может быть разложен по выбранному базису:

(7)      ,

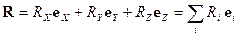 т.е. представлен как сумма единичных ортов, домноженных на числа, называемые проекциями вектора на направление орта (рис. 16_5). Выражение для проекций получается с учетом (6) в результате скалярного умножения (7) на каждый из ортов:

(8)     .

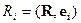     В функциональном пространстве роль векторов играют  непрерывные функции, роль скалярного произведения (операция, ставящая в соответствие двум векторам число) - интеграл по конфигуранционному пространству аргументов от их произведения:

(9)       .

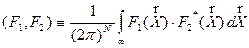Роль ортонормированного базиса может играть множество гармонических функций:

(10)     ,

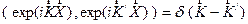причем дельта функция в (10) является аналогом символа Кронекера в (6). Теорема о разложении в интеграл Фурье, имеющая вид:

(11)    

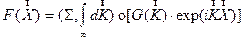
аналогична разложению (7), причем амплитуды волн (“проекции функции F на гармонические отры”) находятся аналогично тому, как это делалось для векторов в (8):

(12)       .

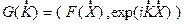        Помимо гармонических функций существует бесконечное множество других ортонормированных наборов, конкретный выбор которых определяется спецификой задачи. В частности,  могут использоваться и дельта-функции, строгое математическое определение которых аналогично разложениям (7) и (11):

(13)           .

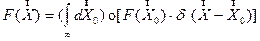      Т.о. с точки зрения математики дельта функции (описывающие точечные частицы) и гармонические функции (описывающие монохроматические волны) составляют ортонормированные наборы и могут использоваться для разложения более сложных функций и одинаково  пригодны для описания объектов и процессов с весьма разнообразными свойствами.

 

      Акустические волны. Звук представляет собой продольные волны сжатия, распространяющиеся в упругих материальных средах. В твердых телах возможен “поперечный” звук. Ухо человека воспринимает колебания, частоты которых лежат в диапазоне от  ??  Гц до  Гц ??. Высота звука определяется частотой колебаний: более высокие частоты вызывают ощущение “более высокого звука”, “басы” соответствуют низкочастотным колебаниям. Ощущение громкость звука определяется энергией, переносимой звуковой волной (пропорциональна квадрату амплитуды колебаний давления).

        Органы слуха млекопитающих представляют собой весьма совершенный акустический прибор, позволяющий регистрировать звук в широких диапазонах громкости (“сила возникающего ощущения” пропорциональна логарифму энергии). Основу “входного устройства” звукового канала составляет акустический резонатор, выделяющий и усиливающий из всевозможных акустических колебаний лишь те, что лежат в диапазоне восприятия. Основная роль в анализе звука принадлежит специальным упругим волоскам различных размеров, связанных с чувствительными нервными окончаниями. Гармонические Фурье-составляющие, на которые можно разложить звуковые колебания, вследствие явления резонанса (резкое увеличение амплитуды колебаний при совпадении собственной и вынуждающих частот) сильно раскачивают волоски строго определенных размеров, что вызывает появления импульсов в соответствующих нервных окончаниях. Соответствующая информация передается в мозг, где и возникает ощущение звука (эта часть процесса восприятия изучена наиболее плохо). Т.о, в ухе происходит фурье-анализ звуковых колебаний.

          Колебания воздуха, создаваемые свободно колеблющимися струнами, весьма близки к гармоническим (”чистый звук”), хотя и содержат малые примеси частот, кратных главной - обертоны. Их наличие объясняет факт различного звучания одной и той же ноты на разных инструментах. Обертоны “несут ответственность” за распознавание речи: при произношении гласных звуков голосовые связки человека создают соответствующие его высоте голоса частоты, весьма богатые обертонами. Движение языка и губ изменяют форму ротовой полости, выполняющей роль акустического резонатора,  и, как следствие, - режимы затухания различных гармоник.

      Музыкальные звуки представляют собой смесь нескольких гармонических колебаний, частоты которых относятся как небольшие целые числа и вызывают у человека приятные ощущения (механизм последнего не выяснен).  Близкие, но отличающиеся по частоте колебания вызывают неприятные ощущения диссонирующего звука. Звуковые колебания со сплошными спектром частот воспринимаются человеком как шум.

       Колебания плотности с частотами, лежащими ниже частотного порога восприятия, называются инфразвуком. Имеются данные о том, что интенсивный инфразвук определенных частот может оказывать весьма неблагоприятное влияние на человека, что по-видимому связано с его резонансным воздействием на протекающие в организме  периодические процессы.

          Акустические колебания с частотами, превышающими порог восприятия, носят названия ультразвука.  Ультразвук широко используется в локации в случаях, когда расстояния до объекта столь малы, что измерение времени распространения электромагнитных волн превращается в трудоемкую задачу. Возникающий при отражении звуковых волн  от движущихся объектов эффект Доплера позволяет определять скорости наблюдаемого объекта

          Видимый свет представляет собой поперечные электромагнитные волны, лежащие в частотном диапазоне от ?? Гц до ??Гц. Вызываемое им ощущение яркости определяется логарифмом энергии световой волны (энергия пропорциональна квадрату амплитуды).  Глаза человека и ряда высших млекопитающих способны осуществлять частотный Фурье-анализ электромагнитного поля, создавая различные ощущения цвета. Изменение цветов при движении по спектру от красного до фиолетового соответствует увеличению частот монохроматических гармоник электромагнитного поля.

     Ниже пределов чувствительности человеческого глаза на шкале частот электромагнитного излучения лежит инфракрасное излучение , непрерывно переходящее в  радиоволны.  Их биологическое воздействие в подавляющем большинстве случаев сводится к эффектам, связанным с нагреванием.  Ультрафиолетовое, рентгеновское и гамма излучения характеризуются частотами, лежащими выше предела зрительного восприятия.

     Возрастание частоты электромагнитного излучения сопровождается увеличением его вредного воздействия на биологические объекты.

      Особенности цветного зрения. Интересной физиологической особенностью зрения является тот факт, что определенным образом подобранная смесь монохроматических излучений может создавать точно такое же ощущение: как другое монохроматическое излучение (смесь красного и желтого цветов воспринимается как оранжевый, а не “красно-желтый”). Объяснение кроется в строении светочувствительных клеток - палочек и колбочек, образующих сетчатку глаза. Более чувствительные палочки реагируют только на энергию световой волны (в сумерках изображения теряют свой цвет), а колбочки содержат три сорта зрительного пигмента, имеющие различные кривые спектральной чувствительности (рис.  16_6). В результате протекающих в них физико-химических процессов при облучении клеток формируются электрические импульсы, величины которых определяются произведением интенсивности световой гармоники на чувствительность пигмента на ее частоте.  Т.о. преобразование световых сигналов при зрительном восприятии с математической точки зрения может рассматриваться как проектирование из бесконечномерного пространства амплитуд Фурье-гармоник электромагнитного поля в трехмерное пространство электрических импульсов. Всякое проектировании на подпространство меньшей размерности сопровождается частичной потерей информации, что и приводит к неоднозначности цветового восприятия.

     Физиологические особенности зрительного восприятия образов. Физико-химические процессы преобразования оптических сигналов в электрохимические являются первым звеном в длинной цепи, приводящей к формированию в сознании зрительного образа. Многие звенья этой цепи изучены весьма неполно.

      Светочувствительные клетки сетчатки  соединены не только с мозгом, на и друг с другом, образуя нейронную сеть, производящую первичную обработку зрительных сигналов и являющуюся вынесенной вперед частью мозга. О сложности процессов формирования зрительного образа говорят следующие особенности нашего восприятия:

1. Оптическая система глаза формирует на сетчатке перевернутое изображение, что не отражается на восприятии. При использовании специальных оптических систем, изменяющих изображение на сетчатке на неперевернутое, человек теряет способность адекватного зрительного восприятия. Через несколько дней пользования такой системой зрительная информация вновь начинает восприниматься нормально.

2. Сетчатка разделена на две примерно равные области, нервные волокна от которых идут в разные полушария мозга. Несмотря на то, что граница раздела приходится на центр зрительного поля, изображение не воспринимается как разорванное на две части.

3. Наличие на сетчатке “слепого пятна” (области, лишенной светочувствительных клеток) не приводит к возникновению незаполненной области в зрительной картине даже при восприятии ее одним глазом.

4.  Ощущение объемного непрерывного образа строится из двух не совпадающих друг с другом мозаичных картин, возникающих на сетчатках глаз.

5. Способность распознавания образов трехмерных объектов по их плоским контурным изображениям и возможность их классификации.

       Последняя, возможно наиболее удивительная способность зрения человека, тесно связана с интенсивно разрабатываемой в математике и технике проблемой распознавания образов.

       Фурье-анализ изображений.  При попадании в поле зрения человека нового объекта, его зрительный образ в сознании возникает весьма быстро, но потом уточняется и достраивается (иногда с исправлением ошибок первоначального восприятия (все любители сбора грибов  знают, как “замирает сердце” при виде гриба, через мгновение “превращающегося” в опавший лист).  Очевидно, что на более ранних стадиях эволюции отмеченное свойство было весьма полезным с точки зрения выживания.

        Указанная особенность хорошо вписывается в концепцию Фурье-анализа изображений, согласно которой обработка нервной системой зрительного образа начинается с разложения описывающей распределение интенсивности на сетчатке глаза функции I(x,y) в пространственный ряд Фурье, Его дальнейший анализ начинается с наиболее медленных пространственных гармоник и состоит в сравнении их амплитуд с “хранящейся в памяти библиотекой образов”.  По результатам анализа сравнительно небольшого числа гармоник делается предварительный вывод об объекте, который впоследствии уточняется в результате анализа высших составляющих.  Наряду с “волновой” существует и “точечная” концепция восприятия зрительных образов, согласно которой изображение воспринимается как совокупность светящихся точек.

 

    Т.о. даже на уровне классического описания с точки зрения математики нет принципиальной разницы между корпускулярным и волновым подходами к  описанию реальности. Различие состоит в выборе набора базисных функций. Правильной формулировкой вопроса к естествознанию в рассматриваемом блоке проблем, по-видимому состоит в том, существуют ли в природе реальные объекты, свойства которых близки (или даже тождественны) свойствам отдельно взятой базисной функции (гармонической или дельта-функции). Классическое естествознание отвечало на так поставленный вопрос утвердительно.

 

 

17. Распространение света

     Электромагнитные волны и световые лучи. Являющаяся решением уравнений Максвелла плоская монохроматическая волна в вакууме представляет собой существующие на бесконечном промежутке времени и занимающие все бесконечное пространство колебания электромагнитного поля, распространяющиеся со скоростью света в направлении, перпендикулярном семейству плоскостей, в каждой точке которых мгновенные значения полей Е и В одинаковы (рис. 17_1). Каждая из таких плоскостей называется волновым фронтом, а наименьшее расстояние между плоскостями, в которых поля находятся в фазе (имеют одинаковые мгновенные значения) называются длиной волны.  Лучом света называется нормаль к волновому фронту, вдоль которой распространяется волна. Обычно луч ассоциируется с образом очень тонкой светящейся линии, что верно лишь в случае, если его поперечные размеры существенно превышают длину волны (для видимого света ок. 500 мкм). При меньших поперечных размерах возникает явление дифракции, превращающее луч в расходящийся пучок.

      В природе истинных плоских монохроматических волн, занимающих все пространство и существующих бесконечно долго во времени, конечно, не существует. Реальные источники света излучают “обрывки синусоид” - световые цуги (рис. 17_2). Чем  длиннее цуг, тем больше он похож на плоскую монохроматическую волну (напомним, что теорема Фурье позволяет рассматривать цуг как совокупность плоских монохроматических волн, увеличение длительности цуга уменьшает число входящих в него гармоник).

     Модель атома Томсона. Идея о существовании неделимых частиц, слагающих вещество, уходит своими корнями в древнегреческую философию. Возникшие на классическом этапе развития естествознания химия и молекулярная теория газов рассматривали вещество как совокупность молекул, а в последствии - атомов (для объяснения химических реакций было необходимо предположение о перестройке молекул, а следовательно - существовании составляющих ее более мелких частиц). В конце 19 века стало ясно, что атомы сами обладают структурой, поскольку способны испускать гораздо более мелкие отрицательно заряженные частицы - электроны. Электрическая нейтральность атома требовала предположения о наличии в нем положительно заряженных частей. Томсоном была предложена модель, согласно которой электроны атома “вкраплены в упругое положительное желе” и способны совершать в нем гармонические колебания. Несмотря на некоторую наивность такой модели, она оказалась весьма работоспособной из-за того, что любая система вблизи положения устойчивого равновесия может совершать колебания, которые в грубом приближении можно считать гармоническими.

     Атом Томсона - пример ошибочной (с точки зрения сегодняшнего взгляда на вещи) модели, приводящей к правильному математическому описанию широкого круга явлений.

     Взаимодействие света с веществом (классическая концепция). Как отмечалось, ускоренно движущийся заряд (в том числе - совершающий гармонические колебания) испускает электромагнитные волны.  Возбуждение свободных колебаний электронов в атоме Томсона  приводит к излучению им света. Наиболее распространено возбуждение за счет теплового движения (лампы накаливания, пламена и т.д.) и при столкновениях с электронами (газоразрядные лампы). 

     Поглощение света в веществе объясняется переизлучением энергии световой волны  раскачиваемыми ею  электронами во всевозможных направлениях и ее частичным переходом в другие формы (тепловую). Конкретный механизм кажется весьма странным с точки зрения “здравого смысла” и связан с тем, что при сложении колебаний одинаковой частоты в зависимости от сдвига фаз суммарное колебание может иметь как большую, так и меньшую амплитуду по сравнению с отдельно взятыми слагаемыми (рис. 17_3). Совершающие вынужденные колебания в переменном поле световой волны электроны переизлучают электромагнитные волны на той же частоте, но сдвинутые по фазе относительно возбуждающей волны (результат расчетов в рамках механики Ньютона). Эти волны, складываясь с  исходной, приводят к следующим эффектам (рис. 17_4):

1. Постепенное затухание исходной волны по мере ее распространения в веществе (поглощение света), происходящее по хорошо согласующемуся с экспериментом закону Бугера:

(1)       ,

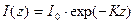где К - коэффициент поглощения, пропорциональный мнимой части комплексного показателя преломления вещества, удовлетворительно рассчитываемого методами классической физики на основе электродинамики и модели Томсона.

2. Изменение эффективной скорости распространения суммарной волны и, как следствие, преломление света на границе двух сред, происходящее по хорошо согласующемуся с экспериментом закону:

(2)        ,

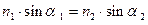где n=v/c - вещественная часть показателя преломления вещества, описывающая отношение фазовой скорости распространения в нем света с скорости света в вакууме.

 3.  Формирование    отраженной волны, распространяющейся под углом, равным углу падения.

4.  Возникновение флуоресценции (излучения в боковых направлениях) в случае образцов небольших поперечных размеров.

      В содержащих свободные электроны металлах эффективные вынужденные колебания зарядов возможны на любых частотах, что объясняет способность этих веществ отражать свет любых частот и являющийся смесью монохроматических белый свет. В диэлектриках электроны связаны с атомами Томсона упругими силами в в соответствии с законами резонанса могут совершать колебания большой амплитуды только на своих (резонансных) частотах. При падении белого света на такие вещества эффективно отражаются лишь некоторые гармоники, что приводит к возникновению окраски. Т.о. при рассматривании своего изображения в зеркале мы в действительности воспринимаем электромагнитное поле  свободных  электронов слоя металла, которые совершают колебания под действием волн, переизлучаемых атомами нашего тела.

     Электромагнитная теория взаимодействия света с веществом предсказала ряд трудно наблюдаемых эффектов, для наблюдения которых потребовалась постановка достаточно сложных экспериментов:

1.  Двулучепреломление - происходит в анизотропных веществах (обычно кристаллах), свойства которых различаются в зависимости от направлений. При распространении световых волн в таких средах оказываются возможными две скорости и, следовательно, два показателя преломления. В результате на границах анизотропных сред лучи света, преломляясь, раздваиваются.

2. Световое давление  возникает при поглощении или переизлучении света веществом вследствие взаимодействия движущегося электрона с магнитным полем световой волны.

3. Генерация кратных гармоник - возникает из-за нелинейности силы, удерживающей электрон в атоме. Помимо основной частоты вынужденных колебаний возникают “обертоны” - удвоенная, утроенная и т.д. частоты, что воспринимается как переизлучение света более высоких частот.

4. Самофокусировка света в веществе - возникает вследствие нелинейностей, приводящих к возрастанию показателя преломления при распространении света большой интенсивности.

5.  Наличие сигнальной волны, свободно распространяющейся (без поглощения) в веществе со скоростью света в вакууме на протяжении очень короткого промежутка времени, пока электроны атомов Томсона не вошли в режим стационарных колебаний (“еще не раскачались”).

     Принцип Ферма. Законы отражения и преломления света на границе раздела двух прозрачных сред удовлетворяют более общему принципу Ферма, согласно которому световые лучи в неоднородной среде имеют форму кривых, при движении вдоль которых свет затрачивает экстремальное (минимальное или максимальное) время на распространение между двумя выбранными точками среди бесконечного множества всевозможных близлежащих путей. Принцип Ферма может быть выведен из волновой теории как ее частное следствие и позволяет правильно описывать распространение света в средах с переменным показателем преломления, в случаях когда само понятие луча имеет смысл. Согласно этому принципу лучи света искривляются в сторону возрастания показателя преломления. Это свойство объясняет ряд “оптических иллюзий”: миражи - искривление световых лучей в слое нагревшегося у раскаленной поверхности песка или асфальта воздуха (рис. 17_5), “запаздывание” захода Солнца за горизонт вследствие искривления лучей неоднородной атмосферой (рис. 17_6) и другие.  В случае существования нескольких близких путей, требующих одинакового времени распространения света, лучи распространяются по каждому из них. На этом основано действие оптической линзы, собирающей испущенный точечным источником света пучок лучей в точку за счет “выравнивания” оптических длин путей (рис. 17_7).

     Экстремальные принципы в физике нередко вызывают недоумение у любителей “пофилософствовать” на около научные темы. По поводу принципа Ферма задается вопрос, откуда свет знает о том, какой путь окажется экстремальным?  При внимательном рассмотрении становится очевидной наивность самой постановки вопроса, поскольку само используемое при формулировке экстремального принципа понятие светового луча является не более, чем грубой моделью с очень ограниченной областью применимости. Свет, как совокупность электромагнитных волн, “подчиняется” не этому принципу, а системе уравнений Максвелла (которая, разумеется, тоже упрощает реальное положение дел), решение которой в некоторых случаях можно наглядно сформулировать в виде принципа наименьшего времени. Т.о. “правильными” были бы вопросы о том, почему приближенно верна система уравнений Максвелла (т.е. следствием какой более общей теории она является) и почему следствия волновой теории в области применимости геометрической оптики удается сформулировать в виде экстремального принципа.

     Ответ на первый вопрос будет обсуждаться в дальнейшем. что касается второго, что любой закон, записываемый в виде математического соотношения

(3)        ,

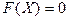может быть переформулирован как экстремальный принцип. Действительно, введение функцию

(4)      

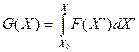
и постановка условия ее экстремальности приводит к выражению

(5)      ,

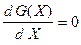математически эквивалентному (3). В случае геометрической оптики получилось так, что функция G(X) оказалась имеющей простой физический смысл (время распространения света).

     Классическая механика Ньютона может быть так же сформулирована как следствие экстремального принципа, согласно которому движущиеся частицы “выбирают” траектории, соответствующие минимальной величине функции Лагранжа ( интеграла от действия):

(6)     .

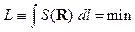      Законы движения тел в искривленном пространстве-времени так же были сформулированы в виде экстремального принципа (минимальности собственного времени).

     Экстремальные принципы широко распространены в современной физике, поскольку позволяют формулировать ее законы в весьма краткой форме.

     Вращение плоскости поляризации света оптически активными веществами является примером “неожиданного”, но на первый взгляд весьма частного явления природы, последующие размышления над которым привели к выводам, выходящим далеко за рамки геометрической оптики. Линейно поляризованными называется электромагнитные волны, вектор электрического поля которых всегда направлен вдоль прямой, определяющей направление поляризации (изображенная на рис. 17_1 волна поляризована в направлении “Х”). Естественный свет, создаваемый традиционными источниками, является хаотической смесью коротких цугов излучения с различной поляризацией. Пропуская такой свет через поляризатор (устройство, гасящее свет одной из линейных поляризаций), можно получить неполяризованый свет. Как показали опыты, проделанные в начале века, ряд растворов имеющих биологическое происхождение веществ (сахар, никотин) обладают удивительной способностью поворачивать плоскость поляризации света  (например, вправо). Повод для удивления состоял в том, что все известные законы физики были инвариантны относительно операции инверсии, меняющей местами “право” и “лево”, и было совершенно непонятно, что “заставляет” свет поворачивать плоскость поляризации в определенном направлении. Удивление еще более возросло после того, как выяснилось, что искусственно синтезированный сахар не обладает способностью вращать плоскость поляризации. Далее оказалось, что живые организмы способны усваивать лишь половину искусственно созданного сахара, а оставшаяся часть вращает плоскость поляризации в противоположном направлении!

     Объяснения естественной оптической активности ряда веществ связано с явлением пространственной изомерии сложных молекул. На рис. 17_8 приведены примеры пространственных изомеров, переходящих друг в друга при  инверсии координат, но не совместимые никакими пространственными вращениями. Независимо от ориентации в пространстве “правовинтовые” молекулы остаются закрученными в правую сторону (на “правый” винт можно наворачивать гайку с правой резьбой любой из ее сторон), что и определяет указанную асимметрию оптических свойств ряда веществ. В химическом отношении “правые” и “левые” изомеры, как и следовало ожидать из симметрии физических законов относительно инверсии, абсолютно эквивалентны (при искусственном синтезе сахара молекулы обеих модификаций возникли в равных количествах). В связи с этим возникает проблема поиска причин асимметрии в веществах, имеющих биологическое происхождение. Считается, что ее возникновение связано со случайностью и способностью к самокопированию биологических объектов: после возникновения первой асимметричной молекулы все последующие стали ее повторять, создавая “глобальную асимметрию вещества”, подобно тому, как создание первых винтов и гаек с правой резьбой впоследствии привело к “правому стандарту” в технике, несмотря на то, что с физической точки зрения право- и левовинтовые соединения эквиволентны.

      Сравнительно недавно в физике элементарных частиц были обнаружены процессы, несимметричные относительно операции инверсии.

 

18. Интерференция и дифракция

        Дифракция света. При внесении тела в заданное электромагнитное поле заряженные частицы начинают совершать вынужденные колебания, излучение от которых вносит искажения в исходное распределение света. В случае тел, размеры которых велики по сравнению с длиной волны, эти процессы хорошо описываются на языке геометрической оптики (как отражение, преломленое и поглощение света). В противном случае принято говорить о явлении дифракции. Строгое (в рамках волновой теории света) решение задачи о дифракции существует лишь для частного случая круглого однородного тела в поле плоской монохроматтической волны (теория Ми) и дается весьма громозкими формулами. Сравнительно простое приближенное решение получается в случае бесконечной поглощающей поверхности (экран) с отверстиями заданной формы и с заданным пропусканием света для точек, достаточно удаленных от них  (дифракция Френеля). Метод решения последней задачи был “угадан” Гюйгенсом, уточнен Френелем и лишь впоследствии был строго выведен Кирхгофом на основе волновой теории и уравнений Максвелла: электромагнитное поле вдали от экрана может рассчитываться как суперпозиция сферических волн, испускаемых каждой его открытой точкой.

       В соответствии с  принципом Гюйгенса-Френеля плоский волновой фронт волны, прошедший через большое отверстие, остается плоским вдали от его краев и изгибается у границы (рис. 18_1). Это означает, что световые лучи (множество нормалей к фронту) у границ отверстия изгибаются (дифрагируют). При уменьшении размеров отверстия роль дифракции возрастает. Отверстия, размеры которого сравнимы с длиной волны, превращает плоскую волну в сферическую. При прохождении света через такие отверстия приближение геометрической оптики становится неприменимым, основанные на ее принципах оптические приборы теряют свою работоспособность. Из-за явления дифракции принципиально невозможно получить оптическое изображение объекта или его деталей, размеры которых не превосходят длины волны излучения.

     Теория Кирхгофа. В основе теории дифракции Френеля лежит математическое тождество, позволяющее связать значения любой являющейся решением уравнения Д’Аламбера  функции E(r) в произвольной точке внутри замкнутой области с ее значениями на поверхности, ограничивающей эту область (интеграл Кирхгофа):

(1)       .

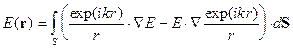Правдоподбное (но не совсем точное) предположение о том, что поле электромагнитной волны за непрозрачным экраном равно нулю, а искажения, вносимые переизлученным полем на открытых отверстиях малы позволяют получить для поля во всех точках за экраном выражение, согласующееся с принципом Гюйгенса-Френеля. На рис 18_2 приведена фотография распределения интенсивности света, дифрагировавшего на небольшом отверстии прямоугольной формы, и результат расчетов интенсивности по формуле (1).

     Интерференция. В предельном случае дифракции на экране с бесконечно-малыми отверстиями (математически описываемыми при помощи дельта-функций) говорят об интерференции, наблюдаемой методом деления волнового фронта. Христоматийным примером подобного рода экспериментов является опыт Юнга (рис. 18_3). В зависимости от разности хода  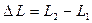вторичные сферические волны, возникающие на отверстиях экрана 1 и 2  при дифракции первичной сферической волны от точечного монохроматического источника S, в точке X происходит сложение или вычитание электромагнитных колебаний. В результате возникает интерференционная картинка в виде чередующихся светлых и темных полос. В 19 веке считалось, что опыты по интерференции являются неопровержимым свидетельством волновой природы света  (при прохождении пучка классических частиц через два отверстия в экране интерференционной картины, очевидно, возникать не может).

     Другим примером сложения колебаний является интерференция в тонких пленках (метод деления волнового фронта), при которой складываются электромагнитные волны, отразившиеся от двух поверхностей (рис. 18_4). В зависимости от соотношения между толщиной пленки и длиной волны излучения наблюдается усиление или ослабление цвета. При освещении белым светом (смесь с различными длинами волн) возникает зависящая от толщины цветная окраска пленки (например, радужные разводы на пятне нефти в воде). Описанный способ окраски используется в природе: пестрая расцветка крыльев бабочек обусловлена не наличием красящего пигмента, а интерференцией света в тонких прозрачных чашуйках крыльев. В технике интерференционные покрытия  используются для создания зеркал с высоким коэффициентом отражения (“диэлектрические зеркала”) и для просветления оптики (гашения волн, отраженных от многочисленных поверхностей линз сложных объективов).

     Интерфереметрические измерения. Высокая чувствительность наблюдаемой картины распределения интенсивностей к разности хода интерферирующих пучков лежит в основе целого класса сверх точных приборов, называемых интерферометрами.

     На рис. 18_5  изображен интерферометр Майкельсона, использованный в решающих экспериментах по проверке постулата о постоянстве скорости света. В приборе сравниваются фазы двух волн, распространяющихся во взаимно перпендикулярных плечах интерферометра. В зависимости от разности хода наблюдается усиление или ослабление света на выходе прибора. Этот прибор может использоваться для прицезионных измерение длины: при перемещении зеркала вдоль измеряемого объекта подсчет "миганий" интерференционной картины позволяет определить длину пройденного пути с точностью до четверти длины волны источника света (около 100 нм). Другим "впечатляющим" применением интерферометра является измерение сверх-малых скоростей движения (несколько сантиметров в год): сползание ледников, дрейф материков и т.д. 

     Поскольку  время распространения света в плечах интерферометра зависит не только от их длин, но и от показателя преломления прозрачной среды, с помощью интерференции можно производить точный анализ наличия малых химических примесей в веществе, вызывающих изменеие показателя преломления.

     Голография нашла применение не только в производстве изопродукции, но и в современной науке и технике. В отличии от фотографии, на которой осуществляется запись распределения интенсивности на плоскости изображения, создаваемого на пластинке методами геометрической оптики, голограмма сохраняет информацию не только об интенсивности слагающих электромагнитное поле волн, но и их фазе. Это позволяет практически полностью восстанавливать электромагнитное поле, создаваемое голографируемым объектом и вызывать зрительное ощущение реального объемного тела. В известном смысле голограмма аналогична зеркалу, продолжающему генерировать изображение после ухода смотревшейся в него девушки).

     Производство высококачественных гологамм стало возможным после создания лазеров - мощных источников монохроматического излучения, способных давать устойчивую интерференционную картину даже при больших разностях хода интерферииующих пучков. При записи голограммы (рис. 18_6) фотографируется сложная интерференционная картина, возникающая при сложении идущей непосредственно от лазера плоской монохроматической волны ("опорной волны") с рассеяной объектом "предметной волны", фронты которой могут представлять собой весьма сложные поверхности.  Считывание проявленной голограммы осуществляется при помощи того же лазера (рис. 18_7). В результате дифракции опорной волны на сложном узоре, возникшем при фотографировании интерференционной картины возникает две симметричные волны, одна из которых практически идентична предметной и формирует мнимое изображение объекта. Вторая волна создает "инвертированное" изображение, которое в практических приложениях стремятся подавить.

      В настоящее время широкое использование нашли толстые голограммы, со слоем фотоэмульсии, существенно превосходящим длину волны записывающего излучения. На такой голограмме регистрируется пространственная структура интерференционной картины. Такая трехмерная структура пропускает через себя только излучение с длиной волны, совпадающей с той, на которой записывалась голограмма. Т.о. для восстановления изображения толстой голограммой нет необходимости в освещении монохроматичесим источником: пластинка сама "выбирает" их белого света составляющую, на которой она создавалась.

     Комбинация из трех голограмм, записанныз в красных, зеленых и синих лучах создает цветное объемной изображение объекта.

     Обращение волнового фронта и динамическая голография.  Проблема обащения волнового вронта (ОВФ) возникла в связи с практически важной задачей фокусировки мощного лазерного излучения на небольших и возможно движущихся объектах (передача энергии, связь, "звездные войны" и т.д.).  Задача еще более усложняется в случае, когда источник излучения и мишень разделены толстым слоем нестационарной атмосферы: статистические флуктуации плотности приводят, согласно принципу Ферма, к искривлению лучей света (или, точнее, к искажению волнового фронта) и расфокусировке пучка.

     Поставленная проблема могла бы быть решена в случае создания хорошо отражающего свет зеркала, поверхность которого принимала бы форму фронта падающей на него волны (ОВФ - зеркала). В этом случае мишень можно было бы облучать сравнительно слабым источником света с широкой диаграммой направленности излучения. Часть фронита отраженной от мишени и искаженной атмосферой волны может быть пропущена через оптический усилитель (слой вещества, усиливающего проходящие через него световые волны, но не изменяющего никаких их характеристик, кроме амплитуды колебаний) и направлена на ОВФ- зеркало (рис. 18_7), при отражении от которого форма волнового фронта не изменится, а направление его распространения изменится на противоположное. После еще одного усиления волна пройдет через все искажающие неоднородности атмосферы в обратном направлении (время распространения света на расстояниях порядка толщины атмосферы намного меньше характерного времени перераспределения неоднородностей) и полностью сфокусируется на мишени.

     Существует несколько подходов к созданию ОВФ - зеркала: гибкая отражающая пленка, форма которой расcчитывается быстродействующим компьютером; обращение волнового фронта, возникающее вследствие нелинейного процесса вынужденного комбинационного рассеяния, голографические методы ОВФ (динамическая голография). Идея последнего подхода очевидна из соображений симметрии: при облучении тонкой голограммы считывающей волной, направленной точно навстречу использованной при записи опорной, одна из двух дифрагированных волн будет распространяться навстречу предметной, т.е. точно в направлении объекта (рис. 18_8). Проблема быстрого (по сравнению со скоростью изменения атмосферы) создания голограммы решается методами нелинейной оптики: существуют вещества, практически мгновенно становящиеся прозрачными под воздействием возникающего в максимумах интерференционной картины излучения большой интенсивности, которые и используются в качестве "фотопластинок" в динамической голографии.

     ОВФ уже сейчас используется в реально действующих экспериментальных установках по управляемому лазерному термоядерному синтезу, где приходится решать задачу одновременной фокусировки разогревающего излучения нескольких сверх мощных лазеров на небольшой дейтериевой мишени. С точки зрения теории решение проблемы ОВФ представляет самостоятельный интерес, поскольку представляет собой пример восстановления упорядоченного излучения после его искажения на хаотической структуре. Иногда о процессе ОВФ говорят как об обращении во времени классически необратимого процесса или даже просто об обращении времени.

    

 

 

19.  19. Волны, фотоны, кванты

     Ультрафиолетовая катастрофа. В конце прошлого столетия у естествоиспытателей начало складываться впечатление, что изучение фундаментальных закономерностей, лежащих в основе научной картины мира, близко к завершению. Это мнение основывалось на несомненных успехах классического естествознания, “подправленного” релятивистской теорией. Учет последней хотя и приводил к несколько неожиданным результатам, но не затрагивал укоренившегося представления о том любая реально существующая система может быть в принципе рассчитана с любой точностью и ее развитие во времени может быть исчерпывающим образом прогнозировано. Вне всякого сомнения, представители точных наук конца 19 века были далеки от попыток рассчитать поведение кошки на основе классической механики и электродинамики, но склонялись к мысли, что трудности подобного расчета носят чисто технический характер.

     На рубеже 19 и 20 веков в физике был сделан ряд открытий, в конечном итоге приведших к коренному пересмотру основных мировоззренческих принципов, лежащих в основе естествознания:

1.    1.     Открытие явления радиоактивности  (превращения атомов различных элементов друг в друга) показало ошибочность представлений об атоме как о неделимом “кирпичике” вещества.  Наиболее важным для последующего развития науки был не столько сам факт обнаружения нового явления (наличие сложной структуры атома и его частей не противоречило принципиальным установкам классического естествознания), сколько возникновение в результате подобных реакций “побочных продуктов”  - различных частиц с высокой энергией, которые удалось использовать в качестве весьма тонкого инструмента для исследований микроструктуры вещества.

2.    2.     Опыты Резерфорда по рассеянию альфа - частиц в тонких пленках вещества (в фольге) показали, что основная масса атома, вопреки модели Томсона, не “размазана” по его объему, а сосредоточена в компактном положительно заряженном теле - ядре. Для объяснения гораздо больших по сравнению с ядром размеров атомов (результаты оценок по плотности конденсированного вещества)  пришлось предположить, что их электроны “вынесены на периферию”. Простейшим объяснением причин, удерживающих электрон от падения на положительное ядро, было предположение об их движении в рамках предложенной Резерфордом планетарной модели атома.

3.    3.     Последовательное описание в рамках классической теории процессов  взаимодействия света с веществом приводило к абсурдному выводу, противоречащему реальным ненаблюдаемым эффектам, о неизбежном перетекании всей энергии от вещества к электромагнитному полю, который получил название ультрафиолетовой катастрофы.. Этот результат возникал как вследствие электродинамического рассмотрения уединенного атома Резерфорда (вращающийся вокруг ядра электрон, как любой ускоренно движущийся заряд, должен излучать энергию в виде электромагнитных волн, что  должно приводить к его падению на ядро через 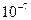с после начала движения), так и в результате термодинамического рассмотрения условия равновесия обладающего конечным числом степеней свободы вещества с излучением, число степеней свободы которого бесконечно (принцип возрастания энтропии требует перетекания энергии из более сосредоточенного  ее состояния в веществе к менее упорядоченное состояние, соответствующее равновероятному распределению по своему бесконечному набору степеней свободы системы “вещество + электромагнитное поле”). Получение одинакового неверного результата в рамках двух различных классических теорий заставляло усомниться в правильности основополагающих принципов, заложенных в из основе.

4.    4.     Опыты показывали, что излучение слабо взаимодействующих друг с другом атомов  (газоразрядная плазма) происходит лишь на определенных дискретных частотах. В простейшем случае атомов водорода наблюдаемые частоты подчинялись очень простой, но никак не объясняемой классической физикой эмпирической закономерности:

(1)  (1)  ,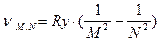

где M и N - любые целые числа.

5.    5.     Опыты по фотоэффекту (явлению выбивания светом электронов с поверхности проводника) указывали, что свет может вести себя подобно частицам и пропорциональной частоте излучения энергией, количество которых пропорционально его интенсивности.

6.    6.     Теплоемкость “идеального газа электронов” в проводящих кристаллах оказывалась исчезающе малой (при нагревании тел входящие в его состав электроны не поглощали энергии на увеличение скоростей хаотического движения, оставаясь “вмороженными”).

7.    7.     Периодическая зависимость химических свойств элементов от зарядов ядер их атомов не могла быть удовлетворительно объяснена классической физикой.

8.    8.     Детерминированность фундаментальных законов классической  физики явно противоречила низкой  предсказуемости поведения биологических объектов.

     Т.о. на рубеже веков накопилось большое количество на первый взгляд разрозненных экспериментальных результатов, не укладывающихся в рамки представлений классической физики. Постепенно возникло понимание того, что причина кроется не в ошибочности отдельных теорий, а в неполноте основополагающих принципов классического естествознания.

     Кванты. Первый шаг на пути к преодолению возникших проблем был сделан Максом Планком на основе детального анализа условий термодинамического равновесия излучения и модельного вещества, представляющего собой ансамбль классических атомов Томсона, имеющих всевозможные резонансные частоты. Выбор простой модели позволил до конца провести все расчеты в аналитическом виде, что существенно облегчило анализ принципиальных ошибок классического описания. Планк установил, что проблема ультрафиолетовой катастрофы может быть снята, если предположить, что энергия совершающих гармонические колебания электронов может принимать не непрерывный, а дискретный  набор значений (рис.19_1):

(2)     ,

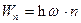где 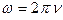  - частота собственных колебаний квазиупругого электрона, n=0, 1, 2, 3, ...- целое число (“номер энергетического уровня”), а константа пропорциональности 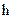 получила название постоянной Планка. При этом обмен энергией между атомом Томсона и излучением оказывается возможным лишь дискретными порциями - квантами, величина которых определяется разностью энергий уровней:

(3)      .

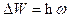Дискретный характер обмена энергией атомов с полем “исключал из игры” огромное число степеней свободы последнего и устранял неизбежное перетекание к ним всей энергии вещества.

     Полученное на основе гипотезы (2) выражение для распределения по частотам энергии теплового равновесного  излучения “спектр излучения абсолютно черного тела” (рис. 19_2):

(4)    

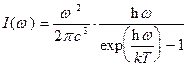
находится в прекрасным согласии с результатами измерений спектров, излучаемых нагретым плотным веществом (раскаленные твердые тела, поверхности звезд и т.д.). В настоящее время формула (4) широко используется для определения температур поверхностей самосветящихся разогретых тел.

    Квантовая гипотеза Планка хорошо согласуется с законами фотоэффекта.

     Предложенная Планком модель с современной точки зрения обладала множеством недостатков, поскольку использовала множество допущений, характерных для классической теории: электромагнитное поле в ней рассматривалось классически, на основе уравнений Максвелла; предполагалось, что распределение атомов по энергиям подчиняется классической статистике Больцмана; наконец сама формула (2) для энергия осциллятора впоследствии оказалась неточной. Несмотря на этом успех гипотезы Планка был предопределен введением ключевого понятия - кванта, дальнейшее развитие которого привело к созданию современной картины естествознания.

     Фотоны.  Рассмотрение электромагнитного поля даже в рамках классической теории позволяет приписать ему “традиционные” для частиц характеристики: энергию и импульс. Квантованный характер обмена энергией между веществом и полем и открытые законы фотоэффекта делали весьма соблазнительной идею рассмотрения поля как совокупности частиц фотонов, рождающихся и гибнущих при излучении и поглощении света соответственно. Поскольку скорость распространения электромагнитного поля в вакууме совпадает с предельным значением с, фотон является ультрарелятивистской частицей с равной нулю массой покоя:  в противном случае импульс фотона был бы бесконечно большим, и процедура загорания на пляже не доставляла бы нам ни малейшего удовольствия:

(5)      .

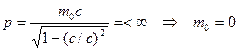     Релятивистское соотношение между энергией и импульсом

(6)     ,

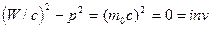получающееся в результате скалярного умножения четырехвектора энергии-импульса (12_9) на себя, приводит к  следующему выражению, связывающему импульс фотона с его частотой:

(7)       .

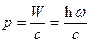     Наличие импульса у фотона позволило изящно и количественно правильно описать явление светового давления как простое следствие закона сохранения импульса при поглощении света веществом.

     Концепция фотонов (корпускулярная модель) привела к большим трудностям при интерпретации экспериментов по интерференции и дифракции,  доказывающих волновую природу света.

     Корпускулярно-волновой дуализм.  Весьма распространено мнение о том, что корпускулярные и волновые свойства света не могут проявляться одновременно: в опытах по интерференции свет ведет себя как волны, а при взаимодействии с веществом - как частицы. О такой “взаимоисключающей двойственности” принято говорить как о корпускулярно - волновом дуализме.

   Отношение к этой проблеме сильно зависит от того, какой смысл вкладывается в понятия “волна” и “частица”.  Например, если называть волной любой объект, описываемый гармонической функцией типа (16_3), а частицей - соответственно объект, описываемый дельта-функцией, то всякий объект природы, допускающий описание при помощи математических функций может рассматриваться либо как совокупность волн, либо -частиц в зависимости от желания. Поскольку помимо указанных существует множество других ортогональных наборы функций, с точки зрения математики последовательный подход требует признания не двойственности, а бесконечной множественности природы как микроскопических, так и макроскопических объектов.

     Традиционная же для физике проблема состоит в попытке разрешить дилемму о том, идентично ли поведение света потоку подчиняющихся механике Ньютона “небольших шариков” - корпускул или оно подобно поведению волн на поверхности воды или звуковых колебаний в воздухе.  При этом вопросы о том, почему свет обязан быть похожим на привычные нам объекты макромира и  почему привычные для нас законы поведения классических частиц и волн не требуют объяснения не задаются.

     Что же касается возможности опыта, в котором одновременно проявлялись бы и волновые и корпускулярные свойства света, то для его осуществления  достаточно в классическом опыте Юнга уменьшить интенсивность источника света (например, до уровня излучения одного фотона в минуту), а для регистрации интерференционной картины использовать пластинку с фотоэмульсией (химическим соединением, зерна которого разрушаются при воздействии света). При такой постановке опыта видно, что каждый фотон на пластинке оставляет зачерненную точку, то есть подобно частице локализован в пространстве. Однако положение засвеченных точек на фотопластинке совершенно не соответствует классическим представлениям о поведении ньютоновских частиц: по мере накопления их количества на пластинке появляется характерная  для классических волн интерференционная картина.

         Принципиальное отличие в поведении фотонов от классических частиц состоит в том, что при наличии интерференции света (оба отверстия в промежуточном экране открыты)  наблюдаемая на фотопластинке  картина не является суммой картин, возникающих при поочередном открывании отверстий (рис. 19_3). Т.о. утверждение о том, что при наличии интерференции  каждый из фотонов пролетает либо через отверстие |1>, либо через отверстие |2> промежуточного экрана не является верным, поскольку принципиально невозможно зарегистрировать прохождение фотона через одну из щелей, не поглотив его. Поглощение же фотона у одной из щелей промежуточного экрана просто означает ее закрытие, что неминуемо приводит к исчезновению интерференционной картины.

      По современным представлениям на вопрос о том, в какую точку фотопластинки |x> попадет излученный источником фотон, теория в принципе не может дать ответа, позволяя лишь рассчитывать только вероятность попадания частицы в рассматриваемую точку. Эта вероятность оказывается пропорциональной классическому значению интенсивности света (квадрату модуля электрического поля), вычисляемому обычными методами решения задач интерференции:

(8)     .

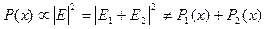     Энергия, переносимая интерферирующими световыми пучками равна произведению энергии одного фотона (3) и числа фотонов, попадающих в рассматриваемую точку (разумеется пропорционального вероятности P(x) ). Таким образом снимается “противоречие” между классическим и планковским выражениями для энергии электромагнитного поля.

     Значение фотонной модели. Предложенная А.Эйнштейном модель фотонов (“частиц, летящих без траекторий”) завоевала большую популярность из-за своей наглядности и до сих пор широко используется при решении задач квантовой механики.  Введенное для объяснения взаимодействия удаленных друг от друга зарядов электромагнитное поле наконец получило “почти зримый образ” совокупности частиц. Наглядность этого “образа” весьма обманчива: свойства фотонов существенно отличаются от привычных свойств частиц, что иногда приводит к недоразумениям даже у специалистов. Более того, может быть поставлена под сомнение целесообразность самой концепции фотонов, поскольку эти “частицы” могут быть зарегистрированы лишь как акт взаимодействия излучения с веществом, в все моменты между излучением и поглощением фотон принципиально ненаблюдаем.

 

       Раздел - 1

                      Мир глазами Исаака Ньютона

 

2.  Пространство и время.

    

     Понятия пространства и времени являются философскими категориями и не определяются в естествознании. Для естественных наук важно уметь определять их численные характеристики - расстояния между объектами и длительности процессов, а так же - описывать их свойства, поддающиеся экспериментальному изучению.

     Измерение расстояний. Проблема ограниченности Вселенной. Измерить расстояние между двумя объектами - значит сравнить его с эталонным. До недавнего времени в качестве эталона использовалось тело, сделанное из твердого сплава, геометрическая форма которого слабо изменялась при изменении внешних условий. В качестве единицы длины был выбран метр, отрезок, сравнимый с характерными размерами человеческого тела. Очевидно, что в большинстве случаев эталон не укладывался целое число раз на длине измеряемого отрезка. Оставшаяся часть измерялась при помощи 1/10, 1/100 и т. эталона. В принципе считалось, что такую процедуру можно продолжать до бесконечности, в результате чего получалось бы точное значение длины, выражаемое бесконечной десятичной дробью, т.е. вещественным числом. (В математике понятие вещественного числа возникло как результат обобщения описанной процедуры измерения длин отрезков).

     На практике многократное деление исходного эталона было невозможно. Для повышения точности измерения и измерения малых отрезков потребовался эталон существенно меньших размеров, в качестве которого по настоящее время используются стоячие электромагнитные волны оптического диапозона.

     В природе существуют объекты, значительно меньшие длин волн оптического излучения (молекулы, атомы, элементарные частицы). При их измерениях помимо неудобства сравнения с  эталоном больших размеров возникает более принципиальная проблема: объекты, размеры которых меньше длины волны электромагнитного излучения, перестают его отражать и, следовательно, оказываются невидимыми.  Для оценки размеров таких мелких объектов свет заменяют потоком каких-либо элементарных частиц (электронов, нейтронов и т.д.). Величина объектов оценивается по т.н. сечениям рассеяния, определяемым отношением числа частиц, изменивших направления своего движения, к плотности падающего потока. Наименьшим расстоянием, известным в настоящее время, является характерный размер элементарной частицы (м). Говорить о меньших размерах, по-видимому, бессмысленно.

       При измерении расстояний, значительно превышающих 1м, пользоваться эталоном длины вновь оказывается неудобно. Для измерения расстояний, сравнимых с размерами Земли, применяют методы триангуляции (определение большей стороны треугольника по точно измеренной меньшей стороне и двум углам) и радиолокации (измерение времени задержки отраженного сигнала, скорость распространения которого известна, относительно момента передачи), Для много больших расстояний (до удаленных звезд и соседних галактик) указанные методы оказываются вновь неприменимы (отраженный радиосигнал оказывается слишком слабым, углы треугольника отличаются от  на слишком малую величину). На столь больших расстояниях наблюдаемыми оказываются только самосветящиеся объекты (звезды и галактики), расстояния до них оценивается исходя из наблюдаемой яркости.

      Размеры наблюдаемой части вселенной имеют размеры порядка м. Вопрос о том, имеют ли смысл большие расстояния сводится к проблемам конечности и ограниченности Вселенной, до сих пор окончательно не решенным космологией. Со времен Ньютона считалось, что окружающий нас мир однороден и не может иметь границ (в противном случае возникал вопрос о их физической природе и о том, “что находится по другую сторону”). Однако, предположение о бесконечности Вселенной, совместно с естественным допущением о равномерном распределении звезд по объему и беспрепятственном распространении света в пространстве, приводил к заведомо абсурдному выводу о бесконечно ярком свечении ночного неба (т.н. парадокс ночного неба). Позднее пришло понимание того, что понятия бесконечности и неограниченности не эквивалентны друг другу (напр. шар не имеет границ, но площадь его конечна).

        Измерение интервалов времени. Возраст Вселенной. Измерить длительность процесса - значит сравнить его с эталонным. В качестве последнего удобно выбрать какой-либо периодически повторяющийся процесс (суточное вращение Земли, биение человеческого сердца, колебание маятника, движение электрона вокруг ядра атома). Долгое время в качестве эталонного процесса использовались колебания  маятника. За единицу измерения времени выбрали секунду (интервал, примерно равный периоду сокращения сердечной мышцы человека).

      Для измерения значительно более коротких времен возникла необходимость в новых эталонах. В их роли выступили колебания кристаллический решетки (кварцевые часы имеют характерный период колебаний в 1нс=  с) и движение электронов в атоме (атомные часы с характерным временем  с ). Еще меньшие времена можно измерять, сравнивая их со временем прохождения света через заданный промежуток. по-видимому, наименьшим осмысленным интервалом является время прохождения света через минимально возможное расстояние (с  ).

          При помощи маятниковых часов возможно измерение временных интервалов, значительно превосходящих 1с (человеческая жизнь длится около с), но и здесь возможности метода не беспредельны. Времена, сравнимые с возрастом Земли (ок. с) возможно оценивать лишь по полураспаду атомов радиоактивных элементов. Максимальным промежутком времени, о котором имеет смысл говорить в нашем мире, по-видимому является возраст Вселенной, оцениваемый периодом в  с (началом существования нашего мира принято считать Большой взрыв, произошедший в весьма малой области пространства, в результате которого возник наблюдаемый сейчас мир, представляющий собой совокупность объектов, разлетающихся от начальной точки; события, произошедшие до Большого взрыва никак не влияют на настоящее и, следовательно, могут не рассматриваться).

      В классическом естествознании, занимающимся главным образом описанием макроскопических (сравнимых с размерами человеческого тела) объектов, предполагается, что процедура измерения основных пространственно-временных характеристик (расстояний и длительностей) в принципе может быть выполнена сколь угодно точно и при этом может практически не влиять на измеряемый объект и происходящие с ним процессы.

          Геометрические свойства пространства и времени. Геометрические свойства пространства изучаются геометрией, традиционно базирующейся на системе аксиом Евклида. В отличие от математики, для естествознания небезынтересен вопрос, соответствуют ли эти аксиомы реальным свойствам нашего пространства (напр. вполне мыслима ситуация, в которой сумма углов треугольника может отличаться от : на рис. 2_1 изображен треугольник, все углы которого прямые). Опыт показывает, что для наблюдателя, движущегося без ускорения вдали от массивных тел, аксиоматика Евклида выполняется с хорошей точностью.

         Важной характеристикой материальных систем является их число степеней свободы (минимальной количество чисел, необходимое для исчерпывающего описания положения объекта в пространстве). Чем большим числом степеней свободы обладает объект, тем более трудоемко его описание. Возникает естественный вопрос о минимальном числе степеней свободы, которым может обладать объект в нашем мире. Опыт показывает, что для не взаимодействующих с другими объектами тел это число равно 3 (тремя степенями свободы обладают, например, элементарные частицы с нулевым спином). Об этом свойстве нашего пространства говорят как о его трехмерности (иногда говорят, что трехмерность означает возможность задания трех взаимно перпендикулярных направлений в пространстве). Число степеней свободы большинства реальных объектов может быть существенно большим (спортивный велосипед с хорошо затянутыми болтами и гайками обладает как минимум 18 степенями свободы), однако при решении многих практических задач “внутренние степени свободы” оказываются несущественными (на финише велогонки положение педалей велосипеда лидера никем не регистрируется). Число рассматриваемых степеней свободы можно существенно сократить вплоть до трех (при движении в пространстве), двух (при движении по поверхности) или одной (при движении вдоль заданной кривой). Реальное тело при этом по существу заменяется моделью материальной точки (тело, размеры и форма которого в рассматриваемой ситуации несущественны).

         Для задания временных характеристик процессов может понадобиться несколько вещественных чисел (жизнь человека можно характеризовать, например, моментами его рождения, свадьбы и смерти). Однако существуют явления, для исчерпывающего временного описания которых достаточно одного числа (напр. распад элементарной частицы, который не имеет длительности, поскольку  не может быть разделен на какие-то промежуточные процессы). Существование таких “элементарных” процессов позволяет утверждать, что время одномерно.

       Аналогично тому, как в пространственном описании вводилась модельное представление о материальной точке, при описании эволюции во времени можно ввести понятие мгновенного события, т.е. процесса, длительностью которого в рассматриваемой ситуации можно принебречь (напр. удар мяча о стену часто можно считать мгновенным, хотя детальное рассмотрение показывает, что это весьма сложный и многоэтапный процесс).

          Относительность свойств пространства и времени. Во времена Ньютона считалось, что свойства пространства и времени абсолютны, т.е. не зависят от наличия материальных тел, протекающих процессов и наблюдателей. Современная физика показала ограниченность таких представлений: геометрические свойства пространства и времени  тесно связаны с наличием и расположением массивных тел, зависят от характера протекающих процессов и даже от состояния наблюдателя. В связи с этим сейчас принято говорить, что свойства пространства и времени относительны.

     В классическом естествознании рассматриваются макроскопические объекты и явления, происходящие в существующих независимо от них и друг от друга пространстве и времени, носящих абсолютный характер.

 

20. 20. Принципы квантовой механики

     Соотношение неопределенности Гейзенберга. Логическим развитием идеи о корпускулярных свойствах света (“волны могут вести себя подобно частицам”)  явилось признание волновых свойств у частиц (электрон, нейтрон, протон и т.д. мало отличаются от фотонов и подобно им могут проявлять волновые свойства).Например, в случае очень близкого расположения небольших щелей в опыте Юнга с источником электронов вместо светового так же возникает интерференционная картина. Рентгеновские лучи (фотоны с очень большой энергией) при дифракции на трехмерной кристаллической структуре дают картинку, сходную с получающейся при дифракции электронов.

     Рассуждения, аналогичные ранее проделанным для интерферирующих фотонов, требуют признания невозможности постановки эксперимента по выяснению через какое из двух отверстий пролетел электрон при условии сохранения интерференционной картины. В отличие от фотона, электрон (или другая элементарная частица) в принципе могут быть зарегистрированы без их обязательного поглощения (например, по рассеянному на них свету).  Однако, любое взаимодействие обладающих малыми частиц с другими телами (даже со светом) неизбежно приводит к существенным изменениям состояний самих наблюдаемых частиц, что ведет к разрушению интерференционной картины (фотоны при рассеянии передают частицам импульс порядка 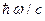,  попытка уменьшения которого за счет уменьшения частоты освещающего излучения неизбежно приводят к потере информации о положении частицы из-за явления дифракции). Многочисленные мысленные эксперименты, подобные рассмотренному приводят к выводу о невозможности одновременного измерения координаты и импульса частиц со сколь угодно высокой наперед заданной точностью. Выражающее принципиальные ограничения на точность измерений неравенство, связывающее минимально возможные погрешности  было предложено Гейзенбергом и носит название соотношения неопределенности:

(1)  (1)     .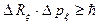

     Соотношение неопределенности Гейзенберга явилось предметом пристального внимания философии, поскольку провозглашаемый принципиальный запрет  перекликался с идеями сторонников агностических учений, отрицающих возможность познания окружающего нас мира. Несмотря на то, что подавляющее большинство естествоиспытателей  уверено в познаваемости мира,  требовался серьезный философский анализ возникшей  проблемы.  По-видимому, выход состоит в признании неприменимости методов описания макроскопических объектов к объектам микромира: если объект не обладает какими-либо характеристиками, то невозможности их точного экспериментального определения вовсе не означает невозможности изучения объекта (бессмысленность попыток получить экспериментально ответ на вопрос о длине хвоста черта не означает невозможности познания мира в целом).  Т.о. соотношение неопределенности является “подсказкой” природы о том, что привычный язык классической кинематики  и динамики Ньютона малопригоден для описания процессов с участием объектов микромира.

     Особенности квантово-механического описания.  “Правила игры” квантовомеханического описания нерелятивистских макро- и микроскопических объектов не могут быть выведены, исходя из “привычных” классических законов, поскольку являются более общими и включают в себя эти классические законы, как частный случай, получаемый в виде чисто математических следствий из постулируемых принципов квантовой механики (принцип соответствия должен выполняться).

Критерием истинности формулируемых принципов, как обычно, является эксперимент и, может быть, красота и  изящность теории (“эта теория достаточно безумна, что бы быть верной”). Следует ожидать, что после завершения разработки еще более общей теории (релятивистской квантовой механики), принципы нерелятивистской теории превратятся в прямые следствия новых, более фундаментальных принципов.

     Наиболее принципиальными отличиями квантовомеханического описания явлений от принятого в классическом естествознании подхода являются:

1.  Отказ от детерминированности  и признание принципиальной роли случайности в процессах с участием микрообъектов. В классическом описании понятие случайности используется для описания поведения элементов статистических ансамблей и является лишь сознательной жертвой полнотой описания во имя упрощения решения задачи. В микромире же точный прогноз поведения объектов, дающий значения его традиционных для классического описания  параметров, по-видимому, вообще невозможен. По этому поводу до сих пор ведутся оживленные дискуссии: приверженцы классического детерминизма, не отрицая возможности использования уравнений квантовой механики для практических расчетов, видят в учитываемой ими случайности результат нашего неполного понимания законов (“внутренних механизмов”), управляющих пока непредсказуемым  для нас поведением микро объектов.  Приверженцем такого подхода, допускающего наличие у квантовых объектов “внутренних степеней свободы”, бал А. Эйнштейн, сформулировавших свою позицию в знаменитом высказывании: ”Я не могу предположить, что бы господь Бог играл в кости”. До настоящего времени не обнаружено никаких экспериментальных фактов, указывающих на существование внутренних механизмов, управляющих “случайным” поведением микрообъектов.

2. Принципиально отличающийся от классического закон сложения вероятностей взаимоисключающих друг друга (с классической точки зрения) событий (например, прохождение электрона через одну из щелей экрана в опыте Юнга). В классической концепции вероятности всегда складываются:

(2)      ,

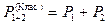что и приводит к не оправдывающемуся на опыте ожиданию обнаружить при открывании двух щелей картины, равную сумме изображений, получаемых от каждой из щелей в отдельности. В кавнтовой механике закон (1) справедлив только в случае, когда существует хотя бы принципиальная возможность установить какое из возможных событий произошло на самом деле (при освещении щелей Юнга коротковолновым излучением можно узнать, по какому пути прошел электрон, закон сложения (1) выполняется и интерференционной картины не возникает). Если же ситуация такова, что события принципиально неразличимы, суммарная вероятность вычисляется как квадрат модуля суммы комплексных функций, называемых амплитудами вероятностей:

(3)      ,

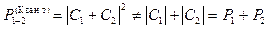при этом вероятности не суммируются, что, например, и наблюдается в экспериментах по интерференции электронов (рис. 20_1). При движении в пустом пространстве амплитуда перехода частицы из одной точки в другую совпадает с выражением для плоской монохроматической волны, частота которой связана с энергией формулой Планка 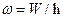. (Сравните формулу (3) с выражением, описывающим интерференцию света  (19_8):  далеко идущие выводы напрашиваются сами собой! Однако, именно здесь уместна большая осторожность: современная квантовая механика является нерелятивистской теорией и из ее законов непосредственно не может быть получено исчерпывающее описание ультрарелятивистской частицы -  фотона.)

3. В квантовой механике отвергается постулируемая в классическом естествознании принципиальная возможность выполнения измерений и даже наблюдений объектов и происходящих с ними процессов, не влияющих на эволюцию изучаемой системы. Это приводит к существованию пар канонически-сопряженных классических параметров, одновременное сколь угодно точное измерение которых оказывается невозможным (к ним относятся уже упоминавшиеся координата - импульс, время - энергия, и др.).

     Законы классической физики получаются из квантовомеханических в пределе больших масс составляющих систему тел. При этом, например, даваемые соотношением неопределенности (1) ограничения на точность оказываются малосущественными:

(4)      .

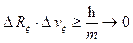Выходящий из имеющей две открытые двери комнаты человек, в принципе, “будет интерферировать” подобно электрону в опыте Юнга, из-за чего возникнут области в пространстве, где он не сможет появиться. однако из-за большой массы человека размеры этих областей будут столь малы (реально много меньше размеров микрочастицы), что для реальных задач макроскопического описания указанное явление заведомо несущественно и даже не наблюдаемо. При рассмотрении же движения электрона (масса всего 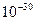 кг) в атоме (характерные размеры около  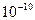м) соотношение неопределенности предсказывает наличие заведомо ненулевого импульса. Соответствующая ему кинетическая энергия оказывается близкой  по порядку величины к потенциальной энергии электростатического притяжения электрона к ядру. При этом соотношение неопределенности “не дает” электрону существенно приблизиться к ядру, поскольку при этом скорость его движения неизбежно должна увеличиться. Т.о электрон в атоме является принципиально квантово-механическим объектом. При квантово-механическом рассмотрении атома даже в рамках полу классической модели Резерфорда проблема ультрафиолетовой катастрофы снимается.

      “Старая” и “новая” квантовые механики. Основная заслуга в строгой формулировке принципов квантовой механики принадлежит Н.Бору. В первоначальном варианте им использовалась планетарная модель атома Резерфорда, в рамках которой движущемуся по круговой орбите электрону сопоставлялись волна, квадрат модуля которой определял вероятность обнаружения электрона в данной точке (“волна ДеБройля”). Бор постулировал существование стационарных орбит, при движении по которым электрон не излучает электромагнитные волны (оказалось, что на таких орбитах укладывается целое число длин волн ДеБройля). При переходе электрона с одной орбиты на другую изменение его энергии сопровождается излучением или поглощением фотона. Такая модель прекрасно объясняла частотные закономерности в спектре излучения атомов водорода (19_5), но еще сохраняла черты отвергаемой классической теории (электроны в атоме имели траектории, которые нельзя наблюдать, не изменяя состояния атома). Теория не могла объяснить некоторых деталей (“тонкой структуры”), обнаруженных при более точных (интерферометрических) исследованиях спектра водорода. Более того, с помощью постулатов Бора не удавалось объяснить наблюдаемые весьма сложные спектры многоэлектронных атомов и их молекулярных соединений. Наконец, “старая” квантовая механика  не объясняла множества других явлений, происходящих с атомами и молекулами, которые были уже хорошо известны в химии.

         Спустя более, чем десятилетие, после создания первой квантово-механической модели атома водорода Н.Бором была построена новая законченная и непротиворечивая квантово-механическая теория, в целом с успехом используемая до настоящего времени. Как это уже не раз случалось в физике, ее создание потребовало развития нового математического аппарата, адекватно описывающего сформулированные  в ее рамках новые физические идеи.

     Математический формализм квантовой механики: состояния, амплитуды, операторы.  Существует несколько альтернативных математических формализмов, отвечающих основным физическим идеям квантовой механики.  Один из подходов состоит в рассмотрении состояний физической системы как векторов в пространстве, размерность которого определяется числом ее взаимоисключающих состояний, называемых базисными (на рис. 20_2  в качестве примера приведены два таких состояния молекулы бензола с различными конфигурациями химических связей, допустимых классической теорией валентности).  Под скалярным произведением двух состояний понимается комплексное число - амплитуда, квадрат модуля которой дает вероятность найти систему в одном из перемножаемых состояний, если точно известно, что она  находится в другом. В примере с молекулой бензола

(5)  (5)  ,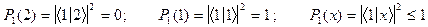

где через 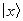обозначено состояние, соответствующее “равномерному распределению химических связей” , к признанию реального существования которого химия шла достаточно долгим путем.

     Для описания измеряемых физических величин F в квантовой механике вводятся операторы 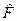, действия которых на векторы состояний в общем случае приводят к появлению новых векторов:

(6)    

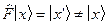
 (так на языку математики описывается тот факт, что процедура измерения оказывает влияние на изучаемую квантово-механическую систему).  Наблюдаемое на опыте среднее значение физической величины в заданном состоянии системы определяется диагональным матричным элементом оператора этой величины:

(7)  (7)       .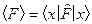

     Т.о. математический аппарат современной квантовой механики ориентирован на вычисления вероятностей пребывания физических систем в тех или иных состояниях и средних значений физических величин, характеризующих эту систему, т.е. как раз те величины, которые могут быть измерены в реальном эксперименте.

     Эволюция во времени квантово-механических систем. Для описания изменения системы во времени вводится оператор эволюции, связывающий ее состояния в два близких момента:

(8)  (8)       .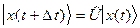

Если оператор эволюции известен, его последовательное применение к исходному состоянии системы позволяет проследить за ее временным развитием, т.е. решить основную задачу естествознания. Обычно оператор эволюции за бесконечно малый  промежуток времени записывают в виде

(9)  (9)  ,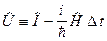

где 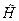 - оператор Гамильтона. Подстановка выражения (9) в (8) приводит к основному уравнению квантовой механики

(10) (10)   ,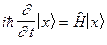

играющему столь же важную роль в квантовой теории, как законы Ньютона в классическом естествознании.  По своему смыслу оператор Гамильтона является обобщением классического понятия энергии, поскольку для частного случая стационарной изолированной системы 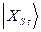 (где энергия сохраняется) уравнение (10) имеет решение

(11) (11) ,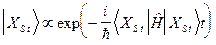

совпадающее с волной ДеБройля и удовлетворяющее стационарному уравнению

(12) (12) .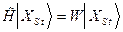

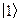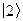     Стационарные состояния квантово-механических систем. При решении уравнения (11) определяются стационарные состояния системы и соответствующие им значения энергии W. В случае дискретного набора разрешенных энергий говорят об энергетических уровнях системы, в случае непрерывного набора - о непрерывном спектре энергий.  Например, базисные состояния  и  молекулы бензола не являются стационарными: являющаяся следствием соотношения неопределенности неточная локализация электронов в пространстве приводит к возможности перехода этих состояний друг в друга (т.н. туннельный эффект).  Уравнение (12) позволяет отыскать два сохраняющихся во времени состояния, которые оказываются симметричной и антисимметричной линейными комбинациями базисных:

(13) (13)  ,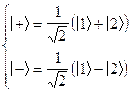

и определить соответствующие им энергии

(14) (14)  .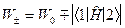

Т.о. наличие возможности переходов между двумя эквивалентными состояниями приводит  к возникновению в системе двух энергетических уровней вместо одного (рис. 20_3). Система может находиться лишь в одном из построенных стационарных состояний ( 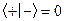 ), но в каждом из них вероятность найти классически осмысленную конфигурацию 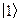 или 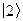 одинакова и равна 0.5. Симметричное стационарное состояние энергетически более выгодно и наиболее часто реализуется в природе.

     Аммиачный мазер.  Существует множество разнообразных систем, обладающих двумя  базисными состояниями, не сохраняющимися во времени. К ним относится молекула аммиака,  с классической точки зрения имеющая две конфигураци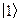и   или 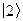, способные превращаться друг в друга из-за туннельного эффекта (рис. 20_4). Стационарные энергетические уровня молекулы разделены зазором, энергетически соответствующем высокочастотному радиоизлучению. Настроенное в резонанс внешнее электромагнитное поле способно вызывать переходы между этими состояниями, которых сопровождаются поглощением или излучением энергии в виде электромагнитных волн (на другом языке - фотонов).  Ансамбль из молекул, находящихся в верхнем энергетическом состоянии способен только излучать энергию, т.е. взаимодействовать с электромагнитным полем, усиливая его. На описанном принципе основана работа первого мазера - лазера, работающего в радио диапазоне излучения.

     Природа химической связи. Системой с двумя состояниями является простейшее химическое соединение - молекулярный ион водорода 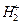 (рис. 20_5). Как и в рассмотренных выше случаях причиной не сохранения во времени выбранных базисных состояний является туннельный эффект. При сближении ядер вероятность туннельного перехода электрона от одного  к другому возрастает , что  приводит к увеличению расстояния между подуровнями и делает симметричное  состояние иона энергетически более выгодным. “Стремясь к снижению полной энергии”, ядра сближаются, что воспринимается как результат действия дополнительной силы, обеспечивающей возникновение химической связи.

     Природа электростатических и ядерных взаимодействий. В общих чертах сходный механизм лежит в основе современных представлений о возникновении электростатических взаимодействий между электрическими зарядами. Вместо “туннелирующего” электрона в молекулярном ионе роль переносчика электрических взаимодействий между зарядами играют виртуальные фотоны, обнаружения которых в реальном эксперименте оказывается принципиально невозможным.

      Сходный механизм был предложен и в случае сильных ядерных взаимодействий. Быстрый спад ядерных сил при увеличении расстояний привел к допущению, что переносчиком взаимодействия является на обладающий нулевой массой покоя фотон, а весьма тяжелая частица с массой,  превосходящей электронную примерно в 200 раз. Вскоре такие частицы были обнаружены в космических лучах (пи-мезоны), но дальнейшие эксперименты показали их непричастность к ядерным силам.  Однако выдвинутая гипотеза все же оказалась жизнеспособной: впоследствии были обнаружены похожие на ранее открытые мезоны частицы, свойства которых согласовывались с предсказанными на основе анализа ядерных сил.

     Электропроводность кристаллов. Системы с двумя состояниями обладают двумя энергетическими подуровнями . Увеличение числа эквивалентных состояний приводит к появлению большего числа подуровней.  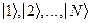Примером системы с большим числом состояний может служить электрон в идеальном кристалле, который может быть локализован вблизи каждого из N регулярно расположенных ионов, что соответствует набору базисных состояний:  (рис. 20_6). Самой низкой энергии соответствует симметричная линейная комбинация базисных состояний:

(15) (15)   ,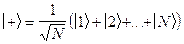

другие ортогональные линейные комбинации дают систему из близкорасположенных друг к другу N энергетических подуровней. При увеличении числа атомов в кристалле подуровни сливаются в сплошную полосу - энергетическую зону, соответствующую непрерывному набору разрешенных значений энергии электрона. Поскольку свободная частица в пустом пространстве так же может обладать энергией из непрерывного набора, поведение электрона в идеальном бесконечном кристалле весьма сходно с поведением свободной частицы. Этим объясняется возможность существования электропроводности в твердых кристаллических телах.

     Уравнение Шредингера.  При описании движения микрочастиц в пространстве в качестве базисного  удобно выбрать непрерывный набор состояний с определенными координатами 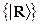, для каждого из которых может быть записано уравнение, аналогичное (10). Конкретный вид оператора Гамильтона для этого случая был правильно угадан Шредингером и имеет вид, аналогичный классическому выражению для механической энергии:

(16) (16) ,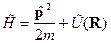

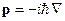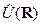где - оператор импульса,  - оператор потенциальной энергии. Наибольший практический интерес представляют вероятности обнаружить находящуюся в стационарном состоянии 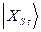 частицу в заданной точке пространства R.  В соответствии с общими правилами квантовой механики эта вероятность дается квадратом модуля соответствующей амплитуды, называемой волновой функцией:

(17) (17)  .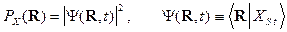

     Анализ математических свойств стационарного уравнения Шредингера

(18) (18)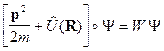

показывает, что в случаях, когда область классически возможного движения частицы в пространстве ограничена, разрешенным является только дискретный набор энергетических уровней. При неограниченном движении энергетический спектр непрерывен.

     В простейшем случае стационарных решений для атома водорода связанным состояниям (электрон находится вблизи ядра) соответствует набор разрешенных значений энергии, полностью совпадающий с вычисленными в рамках первой модели Бора и прекрасно согласующийся с экспериментом (рис. 20_7).  В ионизованном состоянии (электрон ушел от ядра на бесконечно большое расстояние) частица может обладать любым значением энергии.

   

21. Атомы и молекулы

     Спин. Принцип запрета Паули.  Строение и свойства атома могут быть объяснены, исходя их обсуждавшихся первопринципов квантовой механики, дополненных еще двумя утверждениями:

1. Помимо трех “классических” степеней свободы, связанных с описанием положения частицы в пространстве (имеется в виду нерелятивистское описание), электрон обладает дополнительной “внутренней” степенью свободы, называемой спином. Соответствующая спину четвертая координата может принимать только два дискретных  значения, которые удобно считать равными +1/2 и -1/2 (вполне допустимы и другие терминологии для обозначения двух базисных состояний: “спин вверх” и “спин вниз”, “вращение вправо” и “вращение влево”, 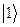 и 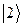,  т.д.).

2. Для электронов строго выполняется принцип запрета Паули, согласно которому невозможно существование двух электронов в одинаковых квантовомеханических состояниях.

     В дальнейшем будет обсуждаться вопрос о глубокой внутренней связи между этими двумя утверждениями.

     Атом водорода. Вырождение энергетических уровней. Наличие у нерелятивистского электрона четырех степеней свободы требует задания его состояния при помощи четырех параметров. Для описания положения электрона в пространстве удобно использовать полярную систему координат с началом отсчета, совмещенным с ядром атома (рис. 21_1). Соответствующие базисные состояния удобно обозначать  как 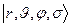.  Сохраняющиеся во времени состояния, получаемые в результате решения стационарного уравнения Шредингера, соответствуют определенным значениям энергии, момента импульса, проекции момента на ось z и одному из двух возможных значений спиновой переменной: 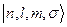.  Принимающие дискретный набор значений параметры, характеризующих стационарное состояние, называются квантовыми числами. Главное квантовое число n определяет энергию электрона в стационарном состоянии:

(1)      .

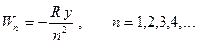( Ry=13.6 эВ - “постоянная Ритберга”). Азимутальное квантовое число  l определяет величину момента импульса , обусловленного орбитальным движением электрона:

(2)    

Магнитное квантовое число m определяет пространственную ориентацию момента импульса (точнее величину его проекции на произвольно заданное направление в пространстве; проекции на другие направления в стационарном состоянии не определены):

(3)      .

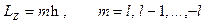     В соответствии с общими правилами квантовой механики вероятность обнаружения в выбранной точке пространства электрона, находящегося в  стационарном состоянии дается квадратом модуля шредингеровской волновой функции. Математические свойства уравнения Шредингера для рассматриваемой системы позволяют представить волновую функцию как произведение двух, зависящих только от расстояния и только от углов соответственно.

(4)    

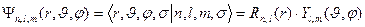
     На рис. 21_2 приведены результаты аналитического расчета нижних состояний электрона в атоме водорода. Как видно, существуют наборы различающихся друг от друга состояний, обладающих одинаковой энергией. Соответствующие им энергетические уровни называются вырожденными. В квантовой механике показывается, что вырождение уровней является следствием наличия у системы симметрии. Уровни атома водорода сильно вырождены из-за высокой симметрии электрического поля, создаваемого практически точечным ядром.

     Проблема описания многоэлектронных атомов. Стационарная теория возмущений. Задача описания квантовомеханических систем, содержащих несколько микрообъектов до сих пор не решена в общем виде. Реальные расчеты проводятся по методу последовательных приближений, в рамках которого осуществляется поэтапный учет имеющихся в атоме взаимодействий по мере убывания их интенсивности. Приближенное решение, полученное на определенным этапе является основой для последующего уточнения вида оператора Гамильтона и соответствующих ему собственных волновых функций. Математическая реализация описанной процедуры в квантовой механике получила название теории возмущений.

     В настоящее время интенсивное развитие вычислительной техники сделало возможным другого, более точного метода численных расчетов многоэлектронных атомов, основанного на использовании экстремальных принципов квантовой механики - метода Хартри и Фока. Для сложных атомов осуществление такого подхода требует использования практически предельных возможностей современной вычислительной техники.

     Нулевое приближение теории возмущений: Периодическая Система Элементов. В рамках нулевого (самого грубого)  приближения теории возмущений учитывается только взаимодействие электронов с ядром и запрет на их эквивалентные состояния, налагаемый принципом Паули. При этом разрешенные для электронов состояния водородоподобны.

     Число электронов в нейтральном атоме, разумеется, должно равняться порядковому номеру элемента, определяемому зарядом ядра. Заполнение “вакантных” мест на энергетических уровнях электронами “регламентируется” стремлением атома (как и любой другой системы) к минимуму энергии и запретом Паули, допускающим нахождение не более одного электрона в каждом из состояний 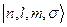.  С учетом соотношений между квантовыми числами легко получить, что на всех состояниях уровня с n=1 может находиться 2  s-электрона, на n=2 - 8  электронов (2 в s-состоянии и 6 p-электронов), группа состояний с n=3 помимо s и p имеют d-оболочку, суммарное число электронов оказывается равным 18 (рис. 21_3).  Находящиеся на верхнем энергетическом уровне электроны наименее сильно связаны с ядром и легче откликаются на внешние воздействия (например, при передаче энергии к атому эти электроны легче возбуждаются, переходя на более высокие свободные энергетические уровни). Именно эти валентные электроны способны участвовать в обменных взаимодействиях, подобных приводящему к образованию молекулярного иона водорода. Поскольку число валентных электронов на верхнем уровне по мере увеличения заряда ядра периодически изменяется от 1 до максимального значения, химические свойства элементов так же обнаруживают периодические изменения.

     Хорошо известно, что указанная закономерность, носящая фундаментальный характер для химии была впервые замечена Д.И.Менделеевым задолго до создания квантовой механики. Найденный им имперический закон позволил предсказать свойства ряда неизвестных в то время элементов, все из которых впоследствии были обнаружены. Квантовомеханическая теория сделала Периодический закон простым математическим следствием уравнения Шредингера, записываемого в весьма грубом приближении, вскрыв смысл составляющих таблицу периодов и групп. Принадлежность элемента к тому или иному периоду определяется главным квантовым числом его заполняемого верхнего уровня. Определяющий максимальную валентность номер группы задается числом электронов на верхнем уровне. Количество элементов в периоде равняется кратности вырождения соответствующего энергетического уровня. С другой стороны, объяснение Периодического Закона было большим успехом квантовой механики, существенно упрочнившей позиции этой “странной теории”, сделавшей наше современное миропонимание таким, как оно есть.

     Первое приближение: термы.  В рамках первой поправки к результатам расчетов многоэлектронных атомов учитывается электростатическое отталкивание электронов и специфическое  влияние принципа Паули, запрещающее двум электронам в одинаковых спиновых состояниях находиться в близких точках пространства. Первый эффект приводит к появлению зависимости энергии уровней от азимутальных квантовых чисел ( несферическое распределение электронной плотности в пространстве ухудшает симметрию создаваемого ядром поля и частично снимает вырождение энергетических уровней ). Второй эффект обуславливает зависимость энергии уровня от взаимного направления спинов электронов внешних энергетических оболочек. Возникающие в рамках этого приближения стационарные состояния получили название термов (рис. 21_4). Приводящее к возникновению термов приближение необходимо учитывать при интерпритации спектров излучения и поглощения света атомами и при анализе тонких химических эффектов, например, связанных с явлением направленной валентности.

      Второе приближение: тонкая структура термов. Детальный анализ спектральных линий показал, что в ряде случаев они оказываются двойными (“дуплеты”), тройными (“триплеты”) и т.д. Это наводило на мысль о энергетическом расщеплении некоторых термов на ряд близко расположенных компонент. Причиной появления такой тонкой структуры (рис. 21_5) являются дополнительные и весьма слабые взаимодействия обусловленных спином магнитных полей электронов с движущимся относительно них ядром (“спин-орбитальное взаимодействие”), с другими движущимися электронами (“взаимодействие спин - чужая орбита”) и со спиновыми магнитными полями других электронов (“спин-спиновое взаимодействие”) и специфические релятивистские эффекты (например, зависимость массы электрона от скорости). Результаты расчетов (носящих главным образом теоретический интерес и являющихся своеобразным тестом нашего понимания строения атома) полностью совпадают с данными спектроскопических измерений.

        Следующее приближение: сверх-тонкая структура. Весьма трудоемкие спектроскопические исследования с использованием интерференционной техники высокого разрешения показывают наличие слабого расщепление компонент тонкой в подуровни сверх-тонкой структуры. Причиной ее появления является взаимодействие очень слабого магнитного поля атомного ядра (обусловленного движением в нем заряженных протонов и наличием спина у всех нуклонов) с движущимися электронами, а так же движение ядра и конечность его размеров. Исследование сверх-тонкой структуры спектральных линий позволяет относительно дешево получить экспериментальную информацию о стуктуре атомного ядра  и протекающих в нем процессах (описанный метод является своеобразным нарушением принципов классической оптики, ограничивающих возможность получения оптической информации об объектах, размеры которых существенно меньше длины волны).

       В простейшем случае атома водорода сверх-тонкая структура уровней может быть рассчитана в рамках квантовой механики абсолютно точно. Вызванное перечисленными эффектами сверх-тонкое расщепление нижнего энергетического уровня водорода имеет величину, соответствующую длине волны радиоизлучения в 21 см. Именно это значение было использовано в качестве масштаба расстояний в космическом послании к инопланетным цивилизациям, помещенном на межпланетную космическую станцию Пионер.

      Еще более тонкие исследования спектра атома водорода показали наличие у него небольшого сдвигя вниз уровней, соответствующих s-состояниям, который не укладывается в рамки “классической квантовой механики” (так называемый Лэмбовский сдвиг). По современным представлениям он мжет быть объяснен лишь в рамках следующей за квантовой механикой более общей теории - квантовой электродинамики.

       Излучение и поглощение света атомами.  Переходы между стационарными состояниями атома возможны при наличии внешнего воздействия, зависящего от времени. Таковым может быть изменяющееся электромагнитное поле световой волны. Вынужденные или индуцированные переходы могут происходить как с излучением, так и с поглощением энергии (обычно в виде одного фотона).  Вероятность таких переходов пропорциональна интенсивности электромагнитного излучения на частоте, совпадающей с энергией перехода. В случае отсутствия внешнего электромагнитного поля переходы между стационарными состояниями атомов в рамках квантовой теории невозможны, поскольку нет возмущения, их вызывающих. Однако, опыт показывает, что в описанной ситуации возможны спонтанные переходы на нижние энергетические уровни с излучением света  В классическую квантовую теорию возможность таких переходов приходится вводить как дополнительный принцип, а их вероятность определять, исходя из вероятности вынужденных переходов и требования возможности термодинамического равновесия атомов с полем.

     Аппарат квантовой механики позволяет рассчитать вероятность вызванных воздействием на атом внешним электромагнитным полем индуцированных переходов, сопровождающихся излучением и поглощением света. Соответствующий математический аппарат носит название нестационарной теории возмущений и учитывает влияние внешнего поля в рамках осуждавшегося метода последовательных приближений.  Обычно расчеты ведутся в первом приближении, дающем выражение для вероятности перехода в единицу времени, зависящее от специфики исходного и конечного уровней и типа излучаемого фотона:

(5)     

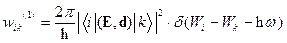
(наличие дельта функции является математическим выражением выполнения закона сохранения энергии при излучении и поглощении фотонов).

     В случаях, когда вероятность переходов в первом приближении по каким-то соображениям (чаще всего вследствие законов сохранения) оказывается малой (“переход оптически запрещен”)

приходится учитывать следующих приближения. Так во втором порядке теории возмущений вероятность перехода зависит не только от характеристик начального и конечного уровня перехода, но и от всех остальных стационарных состояний:

(6)    

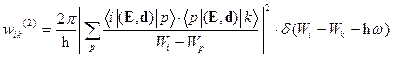
В большинстве случаев в сумме ославляется небольшое число слагаемых, дающих главный вклад в амплитуду перехода. Некоторая схожесть выражений для амплитуд в первом и втором порядках позволила говорить о (6) как о переходе через виртуальный промежуточный уровень. Этот термин носит чисто формальный характер: в промежуточное состояние система реально не переходит: для этого состояния даже не выполняется закон сохранения энергии. Тем ни менее концепция виртуальных состояний широко используется из-за своей наглядности.

     Двухатомные молекулы. Простейшей двухатомной молекулой является молекула водорода, обладающая двумя эквиволентными  состояниями, отличающимися друг от друга перестановкой электронов (рис. 21_6). Механизм возникновения химической связи аналогичен рассмотренному для иона водорода с той только разницей, что запрет Паули требует нахождения электронов в различных квантовомеханических состояниях. Из-за этого связанное состояние молекулы возникает только в случае противоположно направленных спинов электронов (в печати недавно  появилось сообщение о уникальном эксперименте по получению макроскопических порций атомарного водорода, неспособного соединяться в молекулы из-за того, что все атомы содержали электроны с одинаковым направлением спина). Механизм возникновения ковалентной  связи в разнообразных химических соединениях аналогичен.

     Оптические спектры молекул более богаты, чем атомные, что с одной стороны связано с меньшей симметрией системы и с появлением возможности новых форм движения (колебаний и вращений ядер) с другой. Суммарная энергия молекулы (рис. 21_7) складывается из трех существенно различающихся по порядку величины составляющих:  энергия электронной оболочки (характерные разности между энергиями стационарных состояний соответствуют оптическому или ультрафиолетовому излучению), энергия колебания ядер (соответствует инфракрасной части спектра) и энергия вращения молекулы как целого (радиочастотный диапозон). В результате вместо характерных для излучения атомов линейчатых спектров молекулы дают полосатые спектры, состоящие из большого числа близкорасположенных линий.

     Квантовомеханические расчеты двухатомных молекул оказываются существенно более трудоемкими, чем расчеты для атомов и за исключением небольшого числа простейших химических соединений пока носят уникальный характер.

     Трехатомные и многоатомные молекулы с точки зрения квантовой механики являются очень сложными системами, практически не поддающимися расчетам с традиционной для атомно-молекулярной физики точностью. Рассмотрениетаких систем обучно носит полу- качественный характер и сводится к анализу свойств их симметрии (теория групп), на основе которого делается выводы о структуре системы энергетических уровней. По-водимому, сложность таких систем делает их объектом изучения естественных наук более высокого уровня: химии и молекулярной биологии.

 

 

                                                                                   Раздел - 4

                        Мир глазами Поля Дирака

26. Объединение идей квантовой механики и релятивизма

       Недостаточность “классической” квантовой механики.  По своему построению квантовая механика является существенно нерелятивистской теорией: используемое в уравнении Шредингера выражение для оператора Гамильтона является обобщением классической формулы для  энергии. Для множества реальных приложений теории (физика кристаллов, химия, биология)  требование малости скоростей не является существенным ограничением: диапозон энергий, с которыми приходится иметь дело в земных условиях недостаточен для разгона объектов до релятивистских скоростей. Однако существует целый ряд разделов естествознания, развитие которых сделало актуальным вопрос о разработке релятивистской квантовой теории. К ним прежде всего следует отнести разделы физики, занимающиеся взаимодействием света с веществом: зародившаяся в результате попыток поняти физическую природу света квантовая механика оказалась неспособной адекватно описать ультрарелятивистскую частицу - фотон. Релятивистская теория микромира необходима физике ядра и элементарных частиц, поскольку изучаемые в ее рамках процессы с участием сильных взаимодействий сопровождаются обменом большими порциями энергии, что неизбежно связано с возникновением высоких скоростей. Космологические теории эволюции Вселенной и Большого Взрыва требуют развития аппарата описания вещества в экстремальных (с нашей точки зрения) состояниях. Наконец, наличие плохо связанных друг с другом релятивистской и квантовой теорий, каждая из которых по-своему “объясняла” классическую концепцию, являющуюся предельным случаем каждой из них, неизбежно ставило вопрос об их объединении. Попытки обобщения квантовой механики и придания ей релятивистски инвариантной формы делались буквально с первых шагов ее создания, но до сих пор еще не привели к созданию законченной и полностью свободной от внутренних противоречий теории.

     S-матрица. Дополнительной сложностью, присущей релятивистской теории является несохранение числа частиц, участвующих в процессе. В частности это означает, что любая рассматриваемая система должная обладать бесконечным числом степеней свободы. Поскольку сама процедура измерения координат частицы в принципе может приводить к рождению новых частиц, она становится принципиально бессмысленной.  Релятивистская квантовая теория отказывается не только от описания пространственного положения микрообъектов,  но и от описания процессов с их участием в виде происходящих последовательно (друг за другом) промежуточных событий. 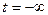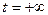Расчеты поддаются лишь амплитуды вероятностей переходов системы из исходного состояния при , в котором все входящие в нее частицы находятся так далеко друг от друга, что взаимодействие между ними пренебрежимо мало в одно из допустимых законами сохранения  конечное состояние при , в котором продукты реакции вновь являются практически свободными объектами. Набор амплитуд таких переходов образует s-матрицу,  вычисление которой и является задачей релятивистской квантовой теории.

      Уравнение Клейна-Гордона было первой удачной попыткой обобщения уравнения Шредингера на случай релятивистского описания электромагнитных взаимодействий микрообъектов. В основе предложенного вывода лежала идея заменить нерелятивистский оператор Гамильтона в уравнении Шредингера

(1)  (1)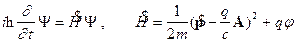       

на его релятивистский аналог, вид которого устанавливался на основании сравнения классических (не квантово-механических)  выражений для релятивистской и нерелятивистской функций Гамильтона:

(2)  (2)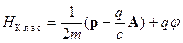            

(3)  (3)          ,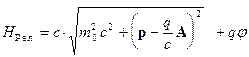

где учтена возможность взаимодействия зарядов с электрическим и магнитным полями, описываемыми потенциалами 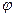 и A.

     Основная математическая трудность, возникающая при попытке перевести релятивистскую формулу  (3) на язык квантово-механических операторов состояла в том, что операция извлечения корня из оператора не определена. Предложенный выход состоял в переходе к уравнению второго порядка, возникающего при возведении в квадрат операторного аналога уравнения  (3), где сам оператор Гамильтона согласно (1) заменялся на оператор дифференцирования по времени:

(4)  (4)    .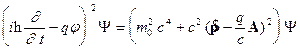

     Полученное таким образом уравнение могло быть легко протестировано на хорошо изученном частном случае описания фотона (q=0, m=0).  Подстановка указанных значений приводит к обыкновенному уравнению Д’Аламбера, описывающему распространение света в вакууме.

     Уравнение Клейна-Гордона в настоящее время считается правильным релятивистским обобщением уравнений квантовой механики, не учитывающих наличие спина у микрообъектов. Оно адекватно оисывает поведение частиц с нулевым спином.

 

27. Уравнение Дирака

      Спин. Спин является важнейшей характеристикой микрообъектов, которая не имеет сколько-нибудь близкого аналога в макроскопическом мире.

     Первыми экспериментами, в которых проявлялось это необычное свойство, были опыты Штерна и Герлаха по взаимодействию обладающих спином объектов с пространственно неоднородным магнитным полем (рис. 27_1). Пучок предварительно никак не ориентированных в пространстве атомов пропускался между полюсами магнита, в результате чего атомы испытывали отклонения в направлении магнитного поля, что было очень похоже на поведении в сходной ситуации небольших макроскопических магнитиков. Наличие внутри атома движущихся зарядов, способных взаимодействовать с магнитным полем, в принципе могло объяснить такое поведение даже на языке классической физики. Несколько странным выглядело лишь то, что исходный пучок не “размывался” в непрерывную полосу (чего следовало ожидать в случае потока произвольно ориентированных относительно поля намагниченных макроскопических частиц), а разделялся на несколько дискретных составляющих, что на классическом языке означало бы наличие дискретного набора разрешенных ориентаций частиц. Нерелятивистская квантовая механика объяснила наблюдаемое явление как результат квантования момента импульса и его проекции на направление магнитного поля. Каждая из возникающих в магнитном поле компонент пучка соответствует определенному значению магнитного квантового числа m, количество которых определяется величиной момента импульса и равно 2l+1. Аналогичное по природе явление наблюдалось в спектрах излучения атомов, помещенных в магнитное поле: спектральные линии расщеплялись на такое же число компонент, соответствующих определенному значению m (эффект Зеемана - снятие вырождения энергий при помещении системы в обладающее весьма низкой симметрией магнитное поле).  Описанные закономерности не выполнялись для атомов с нечетным числом электронов : например, пучки из атомов первой группы в наинизшем s-состоянии расцеплялись на две компоненты, хотя и не обладали вообще никаким  моментом.

     Для разрешение возникшего противоречия была высказана гипотеза о существовании у электрона собственного момента количества движения, названного спином. Очень грубая классическая аналогия позволяет сравнить обладающий спином электрон с планетой, совершающей помимо орбитального движения вокруг звезды, вращение вокруг своей оси. Вращающийся электрически заряженный шарик, в принципе, может участвовать в магнитных взаимодействиях, однако классические оценки показывают, что для количественного объяснения наблюдаемых эффектов скорость движения его поверхности должна превышать скорость света. Т.о. в нерелятивистскую квантовую механику спин был введен как дополнительное свойство бесструктурных частиц, объяснение природы возникновения которого не могло быть получено на основании принципов теории.

     Уравнение Паули. Формальное описание поведения электрона во внешнем магнитном поле, обусловленное наличием у него спина, было достигнуто в рамках модификации нерелятивистского уравнения Шредингера, предложенной Паули. Идея состояла в замене шредингеровской воновой функции двухкомпонентным вектором

(1)     ,

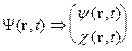удовлетворяющему несколько видоизмененному уравнению:

(2)       ,

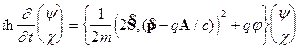где  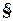- оператор спина, действие которого переводит компоненты волновой функции друг в друга, конкретный вид которого был установлен исходя из анализа результатов опытов Штерна - Герлаха и достаточно общих соображений о поведении системы с двумя базисными состояниями при вращениях в пространстве системы координат. Нахождение электрона в одном из возможных спиновых состояний (при обсуждении концепции классической квантовой механики для них использовались обозначения 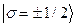)  отождествляется с описанием его при помощи одной из двух компонент волновой функции.

     Уравнение Паули правильно описывает поведение нерелятивистского электрона во внешнем магнитном поле.

       Уравнение Дирака. Предложенное П.Дираком уравнение является обобщением уравнения Паули на случай движения заряженных частиц со спином 1/2  с  релятивистскими скоростями. К его конкретному виду можно прийти на основе сопоставления уравнений Шредингера, Клайна-Гордона и Паули:

 

------------------------------------------------------------------------------------------------------------------------------

*********       Спин не учитывается                                                  Учет наличия спина

------------------------------------------------------------------------------------------------------------------------------

                                            Нерелятивистская теория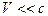    

                                                

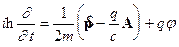
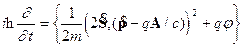
      (уравнение Шредингера)                                                                        (Уравнение Паули)

------------------------------------------------------------------------------------------------------------------------------

                                             Релятивистская теория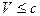   

           

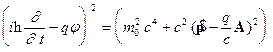
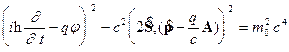
   (уравнение Клейна-Гордона)                                                                  (Уравнение Дирака)

------------------------------------------------------------------------------------------------------------------------------

Для сокращения записи уравнения приведены в операторном виде: сами волновые функции отсутствуют (напомним, что содержащие оператор спина уравнения в правом столбце таблицы подразумевают наличие двух компонент у волновых функций).

      С точки зрения математики уравнение Дирака является дифференциальным уравнением второго порядка в частных производных. Чисто тождественными преобразованиями оно может быть сведено к системе из двух уравнений первого порядка. Последние можно объединить в одно уравнение первого порядка, связывающее четырехкомпонентные волновые функции. Релятивистское обобщение уравнения Паули приводит к необходимости допустить существование четырех  допустимых внутренних состояний электрона вместо двух, постулируемых в классической теории.

      Уравнение Дирака дает правильное количественное описание таких “тонких” эффектов атомно-молекулярной физики, как спин-орбитальное взаимодействие и позволяет верно рассчитывать поправки к энергиям атомных уровней, обусловленные релятивистской зависимостью массы от скорости. Написанные по аналогии с решением задачи для электрона выражения для описания магнитного взаимодействия ядра с электронами (изначально ниоткуда не следует, что тяжелые частицы, составляющие ядро должны подчиняться тем же уравнения, что и электроны) дают правильное описание сверх тонкой структуры спектральных линий. Уравнение Дирака подчиняется принципу соответствия: его разложение в ряд по малому параметру

(3)     

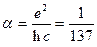
(“постоянная тонкой структуры”) в нулевом приближении приводит к уравнению Шредингера, а в первом - к уравнению Паули.

        Помимо успешного объяснения известных из экспериментов фактов уравнение Дирака предсказывало ряд неизвестных в то время эффектов, весьма странных даже с точки зрения квантовой механики.

      Дираковский вакуум. Наличие четырехкомпонентной волновой функции в уравнении Дирака означало возможность четырех  различных состояний свободного электрона в заданной точке пространства, два из которых интерпретировались как различные ориентации спина. С другой стороны, записанное для свободной частицы уравнение предсказывало возможность двух отличающихся знаком значений энергии:

(4)       .

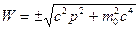Отрицательные энергии возникали и в неквантовой теории, но отбрасывались как физически бессмысленные решения. После того, как в решении уравнения Дирака эти состояния появились “наравне” с экспериментально зарегистрированными спиновыми, идея их простого отбрасывания стала непривлекательной.

     Если в случае свободной частицы разрешенные  по Дираку энергии представляли собой две полубесконечные непрерывные полосы, разделенные интервалом 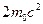, то для частиц в ограниченном пространстве возникали дискретные энергетические уровни (рис. 27_2).  Признание наличия нижних состояний ставило вопрос о причинах, запрещающих “падение” на них реально существующих электронов. Такой процесс должен был бы сопровождаться выделением колоссальной по масштабам микромира энергии, превосходящей .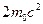

       Дирак высказал предположение, что бесконечная группа уровней с отрицательными энергиями полностью заполнена  электронами, существование которых нами никак не регистрируется. Это означало превращение  “пустого” вакуума Ньютона в весьма сложную систему, содержащую “половину всего сущего” - в вакуум Дирака.

       Антивещество. При передаче находящемуся на “отрицательном уровне” электрону достаточной энергии (например, от электромагнитного поля) он может перейти в состояние с положительной энергией и стать наблюдаемым. При этом на нижнем уровне останется незаполненное вакантное место - “дырка”, поведение которой должно быть сходно с обладающей положительным зарядом частицей (аналогом дырки может служить пузырек в бокале шампанского, движущийся против действия силы тяжести: на самом деле при этом жидкость опускается вниз, а место, где ее нет - перемещается наверх).

     Первоначально предполагалось, что дырками в дираковском вакууме являются протоны, единственные известные в то время элементарные частицы с противоположным электронному зарядом и спином 1/2. Различие масс объяснялось сильным взаимодействием между заполняющими нижние уровни электронами. Этой соблазнительной модели (еще одно “великое объединение”) не суждено было выжить: на эксперименте процесс перехода электрона на нижний уровень, воспринимаемый как взаимное уничтожение (аннигиляция) электрона с протоном

 (5)    

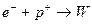
ни кем никогда не наблюдался.

     Спустя небольшой промежуток времени после того, как был поставлен вопрос реальном существовании и физическом смысле дырок К.Андерсон, занимавшийся фотографированием треков приходящих из космоса частиц в магнитном поле обнаружил след неизвестной ранее частицы, по всем параметрам тождественной электрону, но имеющей  заряд противоположного знака.  Частица была названа позитроном. При сближении с электроном позитрон аннигилирует с ним на два фотона высокой энергии (гамма-кванта), необходимость возникновения которых обусловлена законами сохранения энергии и импульса:

(6)      .

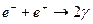     Впоследствии оказалось, что практически все элементарные частицы (даже не имеющие электрического заряда) имеют своих “зеркальных” двойников - античастицы, способные аннигилировать с ними. Исключение составляют лишь немногие истинно нейтральные частицы, например фотоны, которые тождественны своим античастицам.

     Интерпретация Фейнмана. Изящная интерпретация античастиц была предложена Р.Фейнманом, по-новому взглянувшим на хорошо известный факт гармонической зависимости стационарных состояний системы от времени:

(7)          .

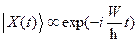В случае античастиц стоящий в выражении для энергии знак минус может быть перенесен на время. Это позволяет рассматривать позитроны как обыкновенные электроны, перемещающиеся во времени в противоположную сторону. На рис. 27_3 изображены мировые линии аннигилирующих на два фотона электрона и позитрона в пространстве Минковского. Поскольку рождение электрон-позитронных пар и их аннигиляция могут происходить параллельно в сразу нескольких точках пространства - времени, возникает соблазнительная возможность объединить их всех одной мировой линией (рис. 27_4), что означает рассмотрение всего множества существующих в данный момент частиц как одной частицы с “изломанной мировой линией”.  Каждое пересечение горизонтальной прямой с такой мировой линией соответствует либо электрону, либо позитрону. Модель Фейнмана удачно подчеркивает замечательный факт абсолютной эквивалентности всех электронов в мире: все они являются одной и той же элементарной частицей.

      Космологический аспект проблемы антивещества. В связи с полной физической симметрией между частицами и античастицами возникает космологическая проблема объяснения причин неравномерной плотности вещества и антивещества во Вселенной. С одной стороны, наличие равных концентраций частиц и античастиц означал бы невозможность устойчивого существования вещества из-за аннигиляции. С другой, остается неясным, “куда делись” соответствующие “непарным” электронам позитроны. Справедливости ради следует отметить, что на сегодняшний день мы не обладаем  достоверной информацией о том, из чего состоят другие звезды: излучаемый атомами вещества и антивещества одинаков. 

      По-видимому все до сих пор прилетающие из космоса метеориты  состояли из “нормального” вещества, поскольку процессы выделения энергии, соответствующей аннигиляции макроскопического тела, к счастью не наблюдались. Из этого не следует вывод о том, что во всем космосе преобладает нормальное вещество: большинство метеоритов приходит к нам из ближнего космоса и имеют родственное происхождение с объектами солнечной системы.

    

28. Фермионы

     Интерференция тождественных частиц. Как отмечалось, все электроны эквиволентны друг другу. Это означает, что в случае системы с несколькими электронами в различных состояниях принципиально невозможно указать, какой из электронов реально находится в каждом из состояний. Общие принципы квантовомеханического описания позволяют описать эту “классически странную” ситуацию весьма просто:  существует множество ортогональных базисных состояний системы (на самом деле неразличимых), соответствующих всевозможным размещениям “мысленно занумерованных” электронов по одноэлектронным состояниям, а реализующееся в природе состояние есть их суперпозиция. Например, простой двухэлектронной системой с двумя состояниями является атом гелия (рис. 28_1), один электрон которого находится на самом нижнем энергетическ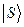ом уровне , а другой - на ближайшем возбужденном уровне 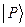. Мыслимы симметричная и антисимметричная линейные комбинации эквиволентных состояний:

(1)      .

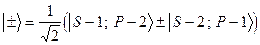     В рамках релятивистской квантовой теории исходя из требований релятивистской инвариантности и положительности числа частиц в системе может быть получен однозначный ответ на вопрос, какое из этих двух состояний реализуется в природе:  амплитуды тождественных частиц с полуцелым спином интерферируют, всегда образуя антисиметричные состояния, в случае систем тождественных частиц с целым спином всегда реализуются симметричные системы . По мнению Р.Фейнмана  сложность доказательства столь просто формулируемого правила свидетельствует о неполноте наших знаний фундаментальных законов природы.

     Фермионы. Из правила интерференции непосредственно следует принцип Паули для электронов: в случае нахождения двух электронов в полностью эквивалентных состояниях (все квантовые числа одинаковы) разность в (1) превращается в 0, что означает равную нулю вероятность реализации такого состояния, т.е. его невозможность.

     Специфическое свойство частиц с полуцелым спином (“фермионов”) не занимать состояния с уже имеющейся частицей видоизменяет функцию их распределения по сравнению с классической статистикой Больцмана:

(2)      .

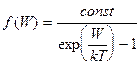Распределение (2) получило название статистики Ферми-Дирака.

     Указанному свойству фермионов наш мир “обязан” своим многообразием: если бы запрета Паули не существовало, элетроны всех атомов собирались бы на самом нижнем энергетическом уровне, химические свойства различных элементов были бы одинаковыми.

      Вырожденный ферми-газ.

 

    

3. Проблема движения

 

     Классификация форм движения. В широком смысле понятие движение используется для обозначения любых изменений, происходящих с объектом или системой объектов с течением времени. Различным уровням организации материи соответствуют свои характерные формы движения (социальные, биологические, химические, физические и т.д.). Высшие формы движения включают в себя более простые и могут быть сведены к их совокупностям (напр. передача возбуждения между нервными клетками организма представляет собой импульсы токов и напряжений, распространяющихся по нейронам, а последние обусловлены движением положительно заряженных ионов Na и K). Простейшей формой является механическое движение, представляющее собой перемещение объектов в пространстве.

        Описание изменяющихся  во  времени  величин. Если какая-либо величина F, которой может быть приписано численное значение, изменяется во времени, это символически записывают в следующем виде:

(1)      .

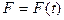     Существует несколько способов задания зависимости F(t), соответствующих различным уровням экспериментального изучения явлений.

      Табличный способ представляет собой набор численных значений измеряемой величины 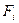    в моменты времени    и наиболее достоверно отражает результаты измерений. В связи с тем, что измеряемые величины не могут быть определены абсолютно точно, корректная запись результатов измерений должна содержать информацию о погрешности в виде доверительного интервала, т.е. численного промежутка, в котором находится истинное значение измеряемой величины с заранее заданной вероятностью (обычно 90%). Ниже приводится пример  табличного задания роста ребенка во времени по результатам измерений, проводившихся по одному разу в год в месяц его рождения:

 

Возраст (годы)         Рост (метры)

                      

..................................................

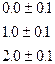
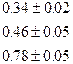
Основным недостатком этого способа является его малая наглядность.

     Графический способ состоит в нанесении точек на график, по осям которого отложены значения величин F и t. “Точки” положено изображать в виде фигур (прямоугольников, эллипсов, крестиков и т.д.), размеры которых отражают погрешность измерений (рис. 3_1). Обычно нанесенные точки соединяют плавной кривой, отражающей представления исследователя (часто весьма субъективные)  о истинном характере зависимости F(t). Интервал между точками на графиках желательно выбирать так, чтобы между ними изображаемая зависимость имела монотонный характер, т.е. не имела минимумов и максимумов.

       Аналитический способ представляет собой описание зависимости F(t) в виде функции, конкретный вид которой подбирается на основе разумного компромисса между требованиями наилучшего соответствия с результатами измерений и простоты формул. Часто качественный вид зависимости априорно известен из теории. При этом выбор рассматриваемых функций существенно сужается, результаты измерений частично учитываются подбором значений подгоночных параметров. Последний способ задания наиболее информативен, но наименее достоверен.

        Производная  и  интеграл. Для характеристики изменения величины F(t) вводится понятие скорости ее изменения (отношение приращения величины к соответствующему интервалу времени при условии, что последний весьма мал):

(2)       .

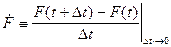Для математической операции (2), носящей название дифференцирования или взятия производной, используется несколько общепринятых обозначений:

(3)       .

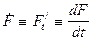     Величина производной числено равна тангенсу угла наклона касательной к графику F(t) (рис. 3_2). В случае возрастания функции F ее производная положительна, при убывании - отрицательна. В точках экстремумов (минимумов и максимумов) производная обращается в нуль. По известной зависимости F(t) производная всегда вычисляется и при том - однозначно (исключение составляют лишь случаи, когда F(t) имеет разрывы, но в реальной природе подобных зависимостей практически никогда не встречается).

     Обратная задача- определение зависимости F(t) по известной скорости ее изменения 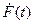  имеет однозначное решение лишь в случае дополнительного задания начального условия (значения величины F в какой-либо момент времени):

(4)      .

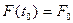     Приращение величины F вычисляется в результате взятия определенного интеграла:

(5)       ,

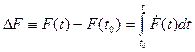числено равного площади под графиком зависимости 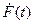  (рис. 3_2). По приращению величины и ее значению, согласно (5), можно найти F(t):

(6)         .

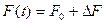      Описание эволюции сложных систем. Системы, имеющие несколько степеней свободы, описываются набором величин 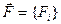 называемых координатами системы (число координат N равно числу степеней свободы). Геометрическим образом состояния системы является точка в N-мерном пространстве конфигураций, координаты которой определяются набором 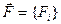. Если система изменяется с течением времени, составляющие набора  изменяются и изображающая точка перемещается в конфигурационном пространстве  =(t).

 

        Векторные и скалярные величины. C математической точки зрения вектором можно называть упорядоченный набор чисел лишь в том случае, если он обладает рядом определенных свойств. В частности, для любых двух таких наборов должны быть определены операции сложения и умножения на число так, чтобы выполнялись следующие свойства:

коммутативности:   

(7)   ,               ,

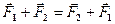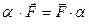ассоциативности:      

(8)   ,      ,

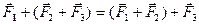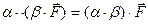и дистрибутивности: 

(9)   ,    ,

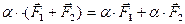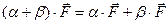Поскольку свойства (7-9) справедливы для операций сложения и умножения вещественных чисел, практически все утверждения из алгебры скалярных величин остаются справедливыми и для векторов. Вектор является обобщением понятия числа на случай многомерных пространств. Скаляры можно рассматривать как векторы в одномерном пространстве.

     Использование векторов позволяет строить описание весьма разнообразных объектов (материальных точек, сил, полей, состояний, численности населения городов, физиологических ощущений и т.д.), используя единообразные математические обозначения

 

     Пользуясь аналогией с соотношениями (1-6), легко определить понятие вектора скорости изменения системы:

(10)   

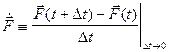
и обобщить все последующие  соотношения на многомерный случай.

      Движение материальной точки в пространстве трех измерений является частным примеров эволюции во времени весьма простой системы, исчерпывающее описание которой дается тремя декартовыми координатами, совокупность которых называется радиус-вектором:

(11)      

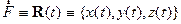
(для обозначения “обычных” векторов в трехмерном пространстве будут использоваться жирные буквы без стрелок).

Сумма векторов определяется  как вектор, составляющие которого являются суммами соответствующих составляющих слагаемых

(12)        ,

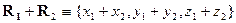а произведение на число - как вектор, составляющие которого получаются домножением составляющих исходного на это число:

(13)        .

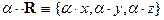Легко убедиться, что все необходимые свойства (7-9) при таком определении операций выполняются. Производная радиус-вектора по времени получила название вектора мгновенной скорости:

(14)         ,

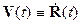а производная скорости - ускорения:

(15)          .

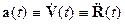По известной зависимости положения тела от времени R(t) его скорость и ускорение определяются однозначно. В случае заданной скорости V(t) для однозначного определения радиус-вектора R(t)  необходимо знать положение тела в какой-то определенный момент времени (“начальное положение”). Если же задана зависимость ускорения от времени, то по ней может быть найдена скорость, а по последней - радиус-вектор. Очевидно, что решение будет однозначным, если заданы начальная скорость и положение тела.

     Относительность механического движения. Однозначное задание радиус-вектора возможно лишь после задания системы координат. Различные системы координат могут по-разному располагаться в пространстве и иметь  различные скорости движения. Получим связь между характеристиками движения материальной точки в неподвижной (0) и движущейся (0’) системах отсчета (рис. 3_3) . Пусть R(t) и R’(t) - радиус-векторы материальной точки в двух системах отсчета, а r(t) - вектор, задающий положений движущейся системы (0’) относительно неподвижной (0). Очевидно, что

(16)      .

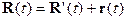Дифференцируя равенство (16) по времени, получаем закон сложение скоростей, позволяющий находить скорость относительно движущейся системы отсчета V’, если заданы скорость движения тела в неподвижной V и относительная скорость движения систем отсчета v:

(17)       .

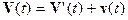Аналогичное соотношение справедливо  и для ускорений.

      Закон (10) показывает, что тело, покоящееся в одной системе отсчета, может двигаться в другой. Т.о. бессмысленно говорить о механическом движении вообще, не указав системы отсчета. Говорят, что механическое движение относительно.

     Закон преобразования координат (16), записанный для частного случая равномерного прямолинейного движения одной системы отсчета относительно другой (рис. 3_4) носит название преобразований Галилея:

(18)       .

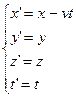Приведенные соотношения с точки зрения здравого смысла кажутся самоочевидными. На сомом деле при их выводе делаются весьма сильные допущения о том, что интервалы времени и длины отрезков одинаковы в обоих системах отсчета.

        Эффект Доплера, являющийся следствием закон сложения скоростей, имеет много интересных проявлений в природе и технике. Пусть какой-либо источник создает с частотой 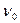 периодическое возмущение (“сигнал”) ,  распространяющееся в пространстве со скоростью C (примером может служить распространение звуковых волн в воздухе). Эффект Доплера состоит в том, что в случае движения источника или приемника частота принимаемого сигнала изменяется. Пусть, например, источник приближается к неподвижному приемнику со скоростью V. Скорость движения сигнала относительно источника, согласно (17), равна c’=c-v. За время между излучением двух последовательных сигналов 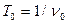 пройденный возмущением путь окажется равным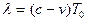(рис. 3_5). Приемник будет регистрировать приход сигналов через время 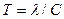, т.е. с частотой

(18)      .

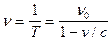     При удалении источника (V<0) регистрируемая частота оказывается меньше исходной (звук, например, будет казаться более низким), при приближении (V>0) - частота возрастает (звук становится более высоким). В случае V=C частота становится бесконечно большой, что в акустике соответствует возникновению ударной волны при движении источника со скоростью звука (т.н. звуковой барьер).  При сверхзвуковом движении формула (18) формально дает отрицательное значение частоты, что соответствует приему сигналов, приходящих в обратном порядке по сравнению с их испусканием.

     В оптике наблюдается сходный эффект, приводящий к изменению частоты излучения (цвета) источника: удаляющиеся источники выглядят “более красными”, приближающиеся - “фиолетовыми” Количественные соотношения несколько отличаются от (18), поскольку при решении задач о движении с около световыми скоростями закон сложения скоростей (17) перестает выполняться. Астрономические наблюдения показывают, что спектры излучения далеких звезд смещены в красную сторону (т.е. частота приходящего от далеких звезд света оказывается заниженной), что служит основой для предположения о разбегании галактик или расширении Вселенной. Измерения сдвигов частот показали, что скорости разбегания звезд пропорциональны расстояниям до них (рис. 3_6):

(19)     ,

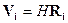где константа H носит названия постоянной Хаббла.

        Утверждение о разбегании галактик ставит два естественных вопроса:

1) Не означает ли соотношение (19) что мы находимся в центре мира?

2) Куда разбегаются звезды?

          Ответ на первый вопрос достаточно очевиден: наблюдатель на любой другой звезде увидит точно такую же картину разбегания. Например, скорость звезды 1 относительно звезды 2, согласно закону сложения скоростей равна

(20)       ,

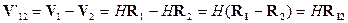что соответствует закону Хаббла. (рис. 3_5).

        Удовлетворительный ответ на второй вопрос, попутно разрешающий парадокс звездного неба, по-видимому состоит в утверждении о глобальной неэвклидовости нашего пространства. Сказанное можно пояснить на модели двумерных существ, оказавшихся на поверхности сферы, радиус которой возрастает во времени (надувающийся шарик). Если на поверхность такой сферы

нанести точки (“звезды”), расстояние между ними будет увеличиваться в полном соответствии с законом Хаббла (прямыми в этом “искривленном мире” следует называть дуги больших кругов на поверхности сферы). Вопрос же о том, куда разбегаются звезды для двумерных существ вообще бессмысленен, поскольку они не способны даже представить истинного вида поверхности, на которой находятся.

 

4. Взаимодействие тел

     Взаимодействие тел. Опыт показывает, что при сближении тел (или систем тел) характер их поведения меняется. Поскольку эти изменения носят взаимный характер, говорят, что тела взаимодействуют друг с другом. При разведении тел на очень большие расстояния (на бесконечность) все известные на сегодняшний день взаимодействия исчезают.

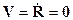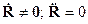     Галлилей первым дал правильный ответ на вопрос, какое движение характерно для свободных  (т.е. не взаимодействующих тел). Вопреки существующему тогда мнению, что свободные тела “стремятся” к состоянию покоя (), он утверждал, что при отсутствии взаимодействия тела находятся в состоянии равномерного движения (), включающего покой как частный случай.

     Инерциальные системы отсчета. В рамках формального математического подхода, реализуемого в кинематике, утверждение  Галилея выглядит бессмысленным, поскольку равномерное в одной системе отсчета движение может оказаться ускоренным в другой, которая “ничем не хуже” исходной. Наличие взаимодействия позволяет выделить особый класс систем отсчета, в которых свободные тела движутся без ускорения (в этих системах большинство законов природы имеют наиболее простую форму). Такие системы называются инерциальными. 

     Все инерциальные системы эквивалентны друг другу, в любой из них законы механики проявляются одинаково. Это свойство было также отмечено Галилеем в сформулированном им принципе относительности: никаким механическим опытом в замкнутой (т.е. не сообщающейся с внешним миром) системе отсчета невозможно установить покоится ли она или равномерно движется. Любая система отсчета, равномерно движущаяся относительно инерциальной тоже является инерциальной.

     Между инерциальными и неинерциальными системами отсчета существует принципиальное отличие: находящийся в замкнутой системе наблюдатель способен установить факт движения с ускорением последних, “не выглядывая наружу”(напр. при разгоне самолета пассажиры ощущают, что их “вдавливает” в кресла).  В дальнейшем будет показано, что в неинерциальных системах геометрия пространства перестает быть евклидовой.

      Законы Ньютона как основа классической механики.  Сформулированные И.Ньютоном три закона движения в принципе позволяют решить основную задачу механики, т.е. по известным начальному положению и скорости тела определить его положение и скорость в произвольный момент времени.

      Первый закон Ньютона постулирует существование инерциальных систем отсчета.

  Второй закон Ньютона утверждает, что в инерциальных системах ускорение тела пропорционально приложенной силе, физической величине, являющейся количественной мерой взаимодействия. Величину силы, характеризующей взаимодействие тел, можно определить, например, по деформации упругого тела, дополнительно введенного в систему так, что взаимодействие с ним полностью компенсирует исходное. Коэффициент пропорциональности между силой и ускорением называют массой тела:

(1)      F=ma

Под действием одинаковых сил тела с большей массой приобретают меньшие ускорения. Массивные тела при взаимодействии в меньшей степени меняют свои скорости, “стремясь сохранить  естественное движение по инерции”. Иногда говорят, что масса является мерой инертности тел (рис. 4_1).

     К классическим свойствам массы следует отнести 1) ее положительность (тела приобретают ускорения в направлении приложенных сил), 2) аддитивность (масса тела равна сумме масс его частей), 3) независимость массы от характера движения (напр. от скорости).

        Третий закон утверждает, что взаимодействия оба объекта испытывают действия сил, причем эти силы равны по величине и противоположно направлены.

       Типы фундаментальных взаимодействий.  Попытки классификации взаимодействий привели к идее выделения минимального набора фундаментальных взаимодействий, при помощи которых можно объяснить все наблюдаемые явления. По мере развития естествознания этот набор менялся. В ходе экспериментальных исследований периодически обнаруживались новые явления природы, не укладывающиеся в принятый фундаментальный набор, что приводило к его расширению (например, открытие структуры ядра потребовало введения ядерных сил).  Теоретические же осмысление, вцелом стремящееся к единому, максимально экономному  описанию наблюдаемого многообразия, неоднократно приволило к “великим объединениям” внешне совершенно несхожих явлений природы (ньютон понял, что падение яблока и движение планет вокруг Солнца являются результатами проявления гравитационных взаимодействий, Эйнштейн установил единую природу электрических и магнитных взаимодействий, Бутлеров опроверг утверждения о различной природе органических и неорганических веществ).

         В настоящее время принят набор из четырех типов фундаментальных взаимодействий: гравитационные, электромагнитные, сильное и слабые ядерные. Все остальные, известные на сегодняшний день, могут быть сведены к суперпозиции перечисленных.

    Гравитационные взаимодействия обусловлены наличием у тел массы и являются самыми слабыми из фундаментального набора. Они доминируют на расстояниях космических масштабов (в мега-мире).

     Электромагнитные взаимодействия  обусловлены специфическим свойством ряда элементарных частиц, называемым электрическим зарядом. Играют доминирующую роль в макро мире и микромире вплоть на расстояниях, превосходящих характерные размеры атомных ядер.

     Ядерные взаимодействия  играют доминирующую роль в ядерных процессах и проявляются лишь на расстояниях, сравнимых с размером ядра, где классическое описание заведомо неприменимо.

     В настоящее время стали весьма популярны рассуждения о биополе, при помощи которого “объясняется”  ряд не очень надежно установленных на эксперименте явлений природы, связанных с биологическими объектами. Серьезное отношение к понятию биополя зависит от того, какой конкретный смысл. Вкладывается в этот термин.  Если понятие биополя используется для описания взаимодействий с участием биологических объектов, сводящихся к четырем фундаментальным, такой подход не вызывает принципиальных возражений, хотя введение нового понятия для описания “старых” явлений противоречит общепринятой в естествознании тенденции к минимизации теоретического описания.  Если же под биополем понимается новый тип фундаментальных взаимодействий, проявляющийся на макроскопическом уровне (возможности существования которого априорно, очевидно, отрицать бессмысленно), то для столь далеко идущих выводов необходимы очень серьезные теоретические и экспериментальные обоснования, сделанные на языке и методами современного естествознания, которые до настоящего времени представлены не были.

       Законы Ньютона и основная задача механики. Для решения основной задачи механики (определение положения тела в произвольный момент времени по известным начальному положению и скорости) достаточно найти ускорение тела как функцию времени a(t). Эту задачу решают законы Ньютона (1) при условии известных сил. В общем случае силы могут зависеть от времени, положения и скорости тела:

(2)     F=F(r,v,t) ,

т.е. для нахождения ускорения тела необходимо знать его положение и скорость. Описанная ситуация в математике носит название дифференциального уравнения второго порядка:

(3)      ,

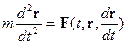(4)     

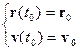
В математике показывается, что задача (3-4) при наличии двух начальных условий (положение и скорость в начальный момент времени) всегда имеет решение и притом единственное. Т.о. основная задача механики в принципе всегда имеет решение, однако найти его часто бывает весьма трудно.

      Детерминизм Лапласа. Немецкий математик Лаплас применил аналогичную теорему о существовании и единственности решения задачи типа (3-4) для системы из конечного числа уравнений для описания движения всех взаимодействующих друг с другом частиц реального мира и пришел к выводу о принципиальной возможности расчета положения всех тел в любой момент времени. Очевидно, что это означало возможность однозначного предсказанная будущего (хотя бы в принципе) и полную детерменированность (предопределенность) нашего мира. Сделанное утверждение, носящее скорее философский, а не естественно научный характер, получило название детерминизма Лапласа. При желании из него можно было сделать весьма далеко идущие философские и социальные выводы о невозможности влиять на предопределенный ход событий. Ошибочность этого учения состояла в том, что атомы или элементарные частицы (“материальные точки”, из которых составлены реальные тела) на самом деле не подчиняются классическому закону движения (3), верному лишь для макроскопических объектов (т.е. обладающих достаточно большими массами и размерами). Правильное с точки зрения сегодняшней физики описание движения во времени микроскопических объектов, какими являются составляющие макроскопические тела атомы и молекулы, дается уравнениями квантовой механики,, позволяющими определить только вероятность нахождения частицы в заданной точке, но принципиально не дающего возможности расчета траекторий движения для последующих моментов времени.

 

 

 

5. Законы сохранения

     Иерархия естественно научных законов. Количество законов природы, сформулированных в естественных науках к настоящему времени, весьма велико. Они неравнозначны.

      Наиболее многочисленным является класс эмпирических законов, формулируемых в результате обобщения результатов экспериментальных наблюдений и измерений. Часто эти законы записываются в виде аналитических выражений, носящих достаточно простой, но приближенный характер. Область применимости этих законов оказывается достаточно узкой. При желании увеличить точность или расширить область применимости математические формулы, описывающие такие законы, существенно усложняются. Примерами эмпирических законов могут служить закон Гука (при небольших деформациях тел возникают силы, примерно пропорциональные величине деформации), закон валентности (в большинстве случаев атомы объединяются в химические соединения согласно их валентности, определяемым положением в Периодической таблице элементов),  некоторые частные законы наследственности ( напр. сибирские коты с голубыми глазами обычно от рождения глухи). На ранних этапах развития естественных наук в основном шло по пути накопления подобных законов. Со временем их количество возросло настолько, что возник вопрос о нахождении новых законов, позволяющих описать эмпирические в более компактной форме.

      Фундаментальные законы представляют собой весьма абстрактные формулировки, непосредственно не являющиеся следствием экспериментов. Обычно фундаментальные законы “угадываются”, а не выводятся из эмпирических. Количество таких законов весьма ограничено (напр. классическая механика содержит в себе лишь 4 фундаментальных закона:  законы Ньютона и закон Всемирного тяготения). Многочисленные эмпирические законы являются следствиями (иногда вовсе не очевидными) фундаментальных. Критерием истинности последних является соответствие конкретных следствий экспериментальным наблюдениям. Все известные на сегодняшний день фундаментальные законы описываются достаточно простыми и изящными математическими выражениями, “не ухудшающимися” при уточнениях. Несмотря на кажущийся абсолютный характер, область применимости фундаментальных законов так же ограничена. Эта ограниченность не связана с математическими неточностями, а имеет более фундаментальный характер: при выходе из области применимости фундаментального законы начинают терять смысл сами понятия, используемые в формулировках (так для микрообъектов оказывается невозможным строгое определение понятий ускорения и силы, что ограничивает применимости законов Ньютона).

       Ограниченность применимости фундаментальных законов естественно приводит к вопросу о существовании еще более общих законов. Таковыми являются законы сохранения. Имеющийся опыт развития естествознания показывает, что законы сохранения не теряют своего смысла при замене одной системы фундаментальных законов другой. Это свойство теперь используется как эвристический принцип, позволяющий априорно отбирать “жизнеспособные” фундаментальные законы при построении новых теорий. В большинстве случаев законы сохранения не способны дать столь полного описания явлений, какое дают фундаментальные законы, а лишь накладывают определенные запреты на реализацию тех или иных состояний при эволюции системы.

         Связь законов сохранения с симметрией системы. Ответ на естественный вопрос о том, почему справедливы законы сохранения в физике был найден сравнительно недавно. Оказалось, что  законы сохранения возникают в системах при наличии у них определенных элементов симметрии. (Элементом симметрии системы называется любое преобразование, переводящие систему в себя, т.е.  не изменяющее ее. Например элементом симметрии квадрата является поворот на прямой угол вокруг оси, проходящей через его центр - “ось вращения четвертого порядка”).

        Глобальные законы сохранения связаны с существованием таких преобразований, которые оставляют неизменными любую систему. К ним относятся:

          Закон сохранения энергии, являющийся следствием симметрии относительно сдвига во времени (однородности времени).

           Закон сохранения импульса, являющийся следствием симметрии относительно параллельного переноса в пространстве (однородности пространства).

    Закон сохранения момента импульса, являющийся следствием симметрии относительно поворотов в пространстве (изотропности пространства).

   Закон сохранения заряда, являющийся следствием симметрии относительно замены описывающих систему комплексных параметров на их комплексно сопряженные значения.

      Закон сохранения четности, являющийся следствием симметрии относительно операции инверсии (“отражения в зеркале”, меняющего “право” на “лево”).

      Закон сохранения энтропии, являющийся следствием симметрии относительно обращения времени.

           Кратко рассмотрим законы сохранения механических величин.

     Закон сохранения импульса. Каждой материальной точке с массой m, движущейся со скоростью V, приписывается векторная характеристика - импульс, определяемый как произведение Массы на скорость:

(1)     .

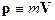Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил:

(2)       .

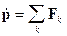В случае системы материальных точек (совокупностью которых можно считать любое реальное тело) полный импульс определяется как векторная сумма всех импульсов

(3)       ,

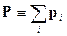Скорость изменения полного импульса определяется суммой внешних сил, действующих на систему (т.е. только сил, описывающих взаимодействие элементов системы с не принадлежащими ей объектами):

(4)    

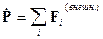
     Системы, на которые не действуют внешние силы, называются замкнутыми. В них полный импульс не изменяется во времени. Это свойство находит большое практическое применение, поскольку лежит в основе принципа реактивного движения (рис. .5_1)..

      В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Однако, этот закон сохранения верен и в случаях, когда Ньютоновская механика неприменима (релятивистская физика, квантовая механика). Как отмечалось, он может быть получен как следствие интуитивно-верного утверждения о том, что свойства нашего мира не изменятся, если все его объекты (или начало отсчета!) переместить на некоторый вектор L. В настоящее время не существует каких-либо экспериментальных фактов, свидетельствующих о невыполнении закона сохранения импульса.

     Закон сохранения момента импульса. Если понятие импульса в классической механике характеризует поступательное движение тел, момент импульса вводится для характеристики вращения. В случае материальной точки, обладающей импульсом p, положение которой задается радиус-вектором R (рис. 5_2), ее момент импульса относительно начала координат равен

(5)        

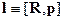
(знаком [,] обозначена операция векторного умножения, в результате которой получается вектор, направленный в соотвествии с правилом правой руки в направлении, перпендикулярном перемножаемым векторам, числено равный 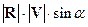). Например, при движении тела по окружности вектор L направлен вдоль ее оси.

      Скорость изменения момента импульса определяется моментом силы (произведением силы на “плечо”):

(6)      .

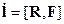Очевидно, что момент импульса сохраняется во времени в случае отсутствия сил или при условии действия сил в направлении R.

     Закон сохранения момента импульса является следствием утверждения о том, что свойства окружающего мира не изменяются при поворотах (или повороте системы отсчета) в пространстве.

      Момент импульса системы  точечных тел L определяется как сумма моментов каждой из точек и сохраняется во времени при условии равенства нулю момента внешних сил.

       В случае твердого тела, вращающегося вокруг неподвижной оси, все его точки движутся по окружностям, центры которых лежат на этой оси. Полный момент ориентирован вдоль оси вращения. Т.о. при отсутствии внешних воздействий  ось вращения тела вместе с L сохраняет свою ориентацию в пространстве. Это свойство используется в навигационных приборах (гирокомпасах).

В случае неравенства нулю момента силы соотношение (6) предсказывает весьма “необычное” с точки зрения “здравого смысла” поведение быстро вращающихся тел ( их момент импульса направлен по оси вращения) с помещенной на острие осью вращения (рис. 5_3).. Такие тела под действием внешних сил (например, силы тяжести) вместо того, чтобы перемещаться в сторону действия силы, начинают медленно вращаться вокруг острия в перпендикулярной приложенной силе плоскости.  Несмотря на то, что подобное поведение является непосредственным следствием законов Ньютона (или еще более общих законов сохранения и симметрии), этот эффект часто не только вызывает удивление у лиц, мало знакомых с точными науками, но и дает им повод рассуждать об “ошибочности  современного естествознания вообще и классической физики в частности.  Основанный на принципе “...если я не понимаю теории или наблюдаемого эффекта, то тем хуже для них...”, к сожалению до сих пор все еще популярен, хотя уже на протяжении нескольких столетий развивающееся естествознание демонстрирует его весьма  низкую эвристическую эффективность.

 

Закон сохранения механической энергии утверждает, что сумма кинетических и потенциальных энергий элементов системы не изменяется во времени при условии, что в системе действуют только потенциальные (консервативные) силы. Этот закон механики является частным случаем более общего закона сохранения энергии, выполняющегося в любой замкнутой (изолированной от внешнего мира) системе. Формулировка закона сохранения энергии обладает меньшей наглядностью по сравнению с законами сохранения импульса и момента, поскольку для  понятия энергии по-видимому невозможно дать исчерпывающего определения даже в рамках классического естествознания. При взаимодействиях между телами энергия может переходить из одной формы в другую и описываться совершенно непохожими друг на друга математическими выражениями. В результате развития естествознания неоднократно открывались новые формы энергии, смысл этого понятия уточнялся.

     Первоначально в механике были введены кинетическая энергия (обусловленная движением тела)

(7)        ,

 

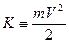и потенциальная (обусловленная взаимодействиями между телами и зависящая от их расположения в пространстве) - U(R). Конкретное математическое выражение для U(R) определяется взаимодействиями между объектами. В большинстве механических систем механическая энергия (сумма K+U) сохраняется во времени (напр. в случае мяча, упруго ударяющегося о пол). Однако нередки и такие системы, в которых механическая энергия изменяется (чаще всего убывает). Для описания  этого были введены диссипативные силы (напр. силы вязкого и сухого трения и др.). Со временем выяснилось, что диссипативные силы описывают не исчезновение или возникновение механической энергии, а переходы ее в другие формы (тепловую, электромагнитную, энергию связи и т.д.). История развития естествознания знает несколько примеров того, как кажущееся нарушение закона сохранения энергии стимулировало поиск  ранее неизвестных каналов ее преобразования, что в результате приводило к  открытию ее новых форм (так, например, “безвозвратная” потеря энергии в некоторых реакциях с участием элементарных частиц послужила указанием на существование еще одной неизвестной ранее элементарной частицы, впоследствии получившей название нейтрино).

     Закон сохранения энергии имеет большое практическое значение, поскольку существенно ограничивает число возможных каналов эволюции системы без ее детального анализа(рис. 5_4). Так  на основании этого закона оказывается возможным априорно отвергнуть любой весьма проект весьма экономически привлекательного вечного двигателя первого рода (устройства, способного совершать работу, превосходящую необходимые для его функционирования затраты энергии).

        Обсуждение смысла оставшихся глобальных законов сохранения требует уяснения менее широко известных концепций современной физики и будет осуществлено ниже в соответствующих разделах настоящего курса.

 

    

 6. Законы движения небесных тел и строение Солнечной системы

     Двумя наиболее значительными успехами классического естествознания, основанного на механике Ньютона, были практически исчерпывающее описание наблюдаемого движения небесных тел и объяснение известных из  эксперимента законов идеального газа.

      Законы Кеплера.  Первоначально считалось, что Земля неподвижна, а движение небесных тел казалось весьма сложным. Галилей одним из первых высказал предположение о том, что наша планета не является исключением и тоже движется вокруг Солнца. Эта концепция была встречена достаточно враждебно. Тихо Браге  решил не принимать участия в дискуссиях, а заняться непосредственным измерениями координат тел на небесной сфере. Он посвятил этому всю свою жизнь, но не только не сделал каких-либо выводов из своих наблюдений, но даже не опубликовал результатов. Позднее данные Тихо попали к Кеплеру, который нашел простое объяснение наблюдаемым сложным траекториям, сформулировав три законов движения планет (и Земли) вокруг Солнца (рис.6_1):

1. Планеты двигаются по эллиптическим орбитам, в одном из фокусов которых находится Солнце.

2. Скорость движения планеты изменяется таким образом, что площади, заметаемые ее радиус-вектором за равные промежутки времени, оказываются равными.

3. Периоды обращения планет одной Солнечной системы и большие полуоси их орбит связаны соотношением:

(1)     .

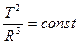     Сложное движение планет на “небесной сфере”, наблюдаемой с Земли, согласно Кеплеру, возникало вследствие сложения этих планет по эллиптическим орбитам с движением наблюдателя, совершающего вместе с Землей орбитальное движение вокруг солнца и суточное вращение вокруг оси планеты.

      Прямым  доказательством суточного вращения Земли был эксперимент, поставленный Фуко, в котором плоскость колебаний маятника поворачивалась относительно поверхности вращающейся Земли.

     Закон Всемирного тяготения. Законы Кеплера прекрасно описывали наблюдаемое движение планет, но не вскрывали причин, приводящих к  такому  движению (напр. вполне можно было считать, что причиной движения тел по кеплеровым орбитам являлась воля какого-либо существа или стремление самих небесных тел к гармонии). Теория гравитации Ньютона указала причину, обусловившую движение космических тел по законам Кеплера, правильно предсказала и объяснила особенности их движения в более сложных случаях, позволила в одних терминах описать многие явления космического и земного масштабов (движение звезд в галактическом скоплении и падение яблока на поверхность Земли).

       Ньютон нашел правильное выражение для гравитационной силы, возникающей при взаимодействии двух точечных тел (тел, размеры которых малы по сравнению с расстоянием между ними):

(2)      ,

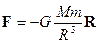которое совместно со вторым законом в случае, если масса планеты m много меньше массы звезды M, приводило к дифференциальному  уравнению

(3)      ,

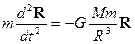допускающему аналитическое решение. Не привлекая каких-либо дополнительных физических идей, чисто математическими методами модно показать, что при соответствующих начальных условиях (достаточно малые начальные расстояние до звезды и скорость планеты) космическое тело будет совершать вращение по замкнутой, устойчивой эллиптической орбите в полном согласии с законами Кеплера (в частности второй закон Кеплера является прямым следствием закона сохранения момента импульса, выполняющегося при гравитационных взаимодействиях, поскольку момент силы (2) относительно массивного центра всегда равен нулю). При достаточно высокой начальной скорости (ее значение зависит от  массы звезды и начального положения) космическое тело движется по гиперболической траектории, в конце концов уходя от звезды на бесконечно большое расстояние.

       Важным свойством  закона гравитации (2) является сохранение его математической формы в случае гравитационного взаимодействия неточечных тел в случае сферически-симметричного распределения их масс по объему. При этом роль R играет расстояние между центрами этих тел.

      Движение небесных тел при наличии возмущений. Строго говоря, законы Кеплера выполняются точно лишь в случае движения лишь одного тела вблизи другого, обладающего значительно большей массой, при условии сферичности этих тел. При незначительных отступлениях от сферической формы (напр. из-за вращения звезды она может несколько “сплющиться”) орбита планеты перестает быть замкнутой и представляет собой прецессирующий вокруг звезды эллипс.

      Другим часто встречающимся возмущением является гравитационное влияние планет одной звездной системы друг на друга. Кеплеровы орбиты являются устойчивыми относительно слабых возмущений, т.е., испытав воздействие от близко пролетающего соседа, планета стремится вернуться на исходную траекторию. При наличии сильных возмущений (пролет массивного тела на небольшом расстоянии) задача о движении существенно усложняется и не может быть решена аналитические. численные расчеты показывают, что в  этом случае траектории планет перестают быть эллипсами и представляют собой незамкнутые кривые.

        Согласно третьему закону Ньютона существует сила, действующая на звезду со стороны планет. В случае M>>m ускорение звезды пренебрежимо мало и ее можно считать неподвижной. При наличии двух тел соизмеримых масс, притягивающихся друг к другу, возможно их устойчивое совместное движение по эллиптическим орбитам вокруг общего центра масс. Очевидно, что более массивное тело совершает движение по орбите меньшего радиуса. В случае движения планет вокруг звезды указанный эффект малозаметен. однако в космосе были обнаружены системы, совершающие описанное движение - двойные звезды. Численный расчет движения планет в системе двойной звезды показывает, что их орбиты существенно нестационарны, расстояние от планеты до звезд быстро меняется в весьма широких пределах. Неизбежные при этом быстрые изменения климата на планетах делает там весьма проблематичной возможность биологической эволюции. Еще менее вероятно возникновение технических цивилизаций на планетах систем двойных звезд, поскольку сложное непериодическое движение планет приводит к трудно расшифровываемому наблюдаемому движению  тел на “небесной сфере”, существенно затрудняя формулировку законов Кеплера и, как следствие, развитие классической механики (рис. 6_2).

     Строение Солнечной системы.  Хорошо известно, что основная масса Солнечной системы (около 99.8%) приходится на ее единственную звезду - Солнце.  Суммарная масса планет составляет только 0.13% от общей. На остальные тела системы (кометы, спутники планет, астероиды и метеоритное вещество) приходится только 0.0003% массы. Из приведенных цифр следует, что законы Кеплера для движения планет в нашей системе должны выполняться очень хорошо. Существенные отклонения от эллиптических орбит могут возникать лишь в случае близкого (по сравнению с расстоянием до Солнца) пролета мимо одной из планет: Меркурия, Венеры, Земли, Марса, Юпитера, Сатурна, Урана, Нептуна или Плутона (особенно это касается самой массивной из планет -  Юпитера). Именно наблюдения возмущения орбиты Нептуна позволили предсказать, а потом и обнаружить Плутон - самую удаленную из известных планет нашей системы.

      Ньютоновский закон гравитации и законы Кеплера позволяют связать размеры орбит планет с периодами вращения, но не позволяют рассчитывать сами орбиты. Еще в 18 веке была предложена эмпирическая формула для радиусов орбит планет солнечной системы:

(4)       ,

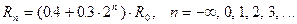где 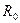 - радиус орбиты Земли. В отличие от законов Кеплера соотношение (4) никак не следует из законов Ньютона и до сих пор не получило теоретического обоснования, хотя орбиты всех известных на сегодняшний день планет удовлетворительно описываются этой формулой. Исключение составляет лишь значение n=3, для которого на рассчитанной орбите планеты не существует. Вместо нее был обнаружен пояс астероидов - небольших по планетным масштабам тел неправильной формы.  Эмпирические законы, не подтвержденные имеющейся теорией, могут играть положительную роль в исследованиях, поскольку тоже отражают объективную реальность (возможно в  несовсем точном и даже в несколько искаженном виде).

     Привлекательной казалась гипотеза о ранее существовавшей пятой  планете - Фаэтоне, разрушенной на куски гигантским гравитационным притяжением ее массивного соседа - Юпитера, однако количественный анализ движения планеты - гиганта показал несостоятельность этого предположения. По-видимому упомянутая проблема может быть разрешена  лишь на основе законченной теории возникновения и эволюции планет Солнечной системы, пока еще несуществующей. Весьма привлекательная теория совместного происхождения солнца и планет из единого газового облака, сжавшегося под действием гравитационных сил, оказывается в противоречии с наблюдаемым неравномерным распределением вращательного момента (момента импульса) между звездой и планетами. Обсуждаются модели происхождения планет в результате гравитационного захвата Солнцем тел, прилетающих из далекого космоса, эффекты, вызванные взрывом сверх-новых. В большинстве “сценариев” развития солнечной системы существование пояса астероидов так или иначе связывается с его близким соседством с самой массивной планетой системы.

      Известные на сегодняшний день свойства планет Солнечной системы позволяют разделить их на две группы. Первые четыре планеты земной группы  характеризуются сравнительно малыми массами и большими плотностями слагающих их веществ. Они состоят из расплавленного железного ядра, окруженного силикатной оболочкой - корой. Планеты обладают газовыми атомосферами. Их температуры главным образом определяются расстоянием до Солнца  и убывают с его увеличением. Начинающаяся с Юпитера группа планет - гигантов  в основном сложена из легких элементов (водорода и гелия), давление которых во внутренних слоях возрастает до огромных величин, вследствие гравитационного сжатия. В результате по пере приближения к центру газы постепенно переходят в жидкое и, возможно, в твердотельное состояния. Предполагается, что в центральных областях давления столь велико, что водород существует в металлической фазе, пока не наблюдавшейся на Замле даже в лабораторных условиях. Планеты второй группы обладают большим числом спутников. У сатурна их число столь велико, что при недостаточном увеличении планета кажется опоясанной системой непрерывных колец (рис. 6_3).

      Проблема существования жизни на других планетах до сих пор вызывает повышенный интерес в околонаучных сферах. В настоящее время можно с достаточной степенью достоверности можно утверждать, что в привычных для современного естествознания белковых формах жизнь на планетах Солнечной системы (разумеется, за исключением Земли) не существует. Причиной этому прежде всего является малость физико-химического диапозона условий, допускающих возможности существования органических молекул и протекания жизненно важных химических реакций с их участием (не слишком высокие и низкие температуры, узкий интервал давлений, наличие кислорода и т.д.).  Единственной, помимо Земли, планетой, условия на которой явно не противоречат возможности существования белковой жизни, является Марс. Однако достаточно детальные исследования его поверхности с помощью межпланетных станций “Марс”, “Марионер” и “Викинг” показали, что жизнь на этих планетах не существует даже в виде микроорганизмов (рис. 6_4).

     Что же касается вопроса о существовании небелковых форм внеземной жизни, его серьезному обсуждению должна предшествавать строгая формулировка самого обобщенного понятия жизни, но эта проблема до сих пор не получила общепризнанного удовлетворительного решения. (Создатся впечатление, что открытие форм жизни, существенно отличающихся от привычных для нашего воображения, вообще может не вызвать сколько-нибудь заметного интереса у ненаучной общественности. Не очень трудно вообразить себе создание компьютерных вирусов, способних размножаться в сетях и способных эволюционировать, гораздо труднее представить реакцию на это в обществе, отличную от досады пользователей, потерявших программы).

      О природе гравитационных сил. Сформулированный Ньютоном закон всемирного тяготения относится к фундаментальным законам классического естествознания. Методологической слабостью концепции Ньютона был его отказ обсуждать механизмы, приводящие к возникновению  гравитационных сил (“Я гипотез не измышляю”). После Ньютона неоднократно предпринимались попытки создания теории гравитации. Подавляющее большинство подходов связано с так называемыми гидродинамическими моделями гравитации, пытающимися объяснить возникновение сил тяготения механическими взаимодействиями массивных тел с промежуточной субстанцией, которой приписывается то или иное название: “эфир”, “поток гравитонов”, “вакуум” и т.д. Притяжение между телами возникает вследствие разряжения Среды, возникающей либо при ее поглощении массивными телами, либо при экранировке ими ее потоков. Все эти теории имеют общий существенный недостаток: правильно предсказывая зависимость силы от расстояния (2), они неизбежно приводят к еще одному ненаблюдаемому эффекту: торможению тел, движущихся относительно введенной субстанции.

     Существенно новый шаг в развитии концепции гравитационного взаимодействия был сделан А. Эйнштейном, создавшим общую теорию относительности.

    

 7. Термодинамическое и статистическое описание классических равновесных ансамблей

       Основания молекулярно-кинетической теории. В настоящее время не вызывают сомнений утверждения, лежащие в основе молекулярно-кинетической теории:

1. Все тела состоят из относительно устойчивых частиц (молекул и атомов);

2. Молекулы находятся в постоянном хаотическом движении;

3. Молекулы взаимодействуют друг с другом.

Эти утверждения носят настолько общий характер, что невозможно указать небольшой набор каких-либо конкретных экспериментов, полностью их доказывающих.

     В пользу первого положения прежде всего свидетельствуют сами факты существования таких разделов естествознания, как химия и молекулярная физика, в которых на оснолве гипотезы о молекулярном строении вещества делается множество конкретных выводов, прекрасно согласующихся с экспериментом. В физике имеется множество косвенных методов, позволяющих определять форму, размеры и расположение молекул, данные этих методов согласуются друг с другом. Созданный сравнительно недавно туннельный микроскоп позволяет визуализовать отдельные атомы и молекулы, расположенные на гладкой поверхности проводящего кристалла.

      Предположение о хаотическом движении молекул впервые было высказано ботаником Броуном, наблюдавшим незначительные перемещения частичек пыльцы цветка, помещенных в жидкость. Методами своей науки Броун убедился в ошибочности своего исходного предположения, что частицы пыльцы являются живыми существами, обладающими способностью самостоятельного движения, и отнес причину их случайных блужданий к передаче импульса в результате случайных ударов со стороны хаотически перемещающихся молекул. Движением молекул объясняется явления диффузии (постепенного перемешивания различающихся веществ вблизи границы их соприкосновения), теплопередачи (постепенное выравнивание температур при соприкосновении горячих и холодных тел), распространения звука и др. В  опыте Штерна была осуществлена непосредственная демонсрация движения молекул горячих паров металла и получена информация о скоростях этого движения.

      Наличием взаимодействия молекул объясняется факт возможности существования вещества в различных агрегатных состояниях. Природа сил, возникающих между молекулами - электрическая. На больших расстояниях полярные молекулы притягиваются друг к другу как электрические диполи, на малых - притяжения сменяется отталкиванием близкорасположенных ядер (рис. 7_1). Как видно, существует два значения межмолекулярных расстояний, при которых любая пара молекул будет находиться в равновесии: Ro и бесконечность. В природе реализуются оба типа равновесных состояний. Первое относится к конденсированным состояниям вещества (т.е. жидкостям и твердым телам; различие между ними состоит в наличии кристаллической решетки у последних), второе - к газообразным состояниям. Очевидно, что при изменении объемов, занимаемых конденсированным веществом, неизбежно возникновение больших внутренних  сил, обусловленных взаимодействиями между молекулами. Возрастание давления газов при изменении объема связано не с наличием сил взаимодействия между его молекулами, а с увеличением частоты ударов молекул о стенки сосуда.

       Основные подходы к описанию макроскопических порций вещества. Поскольку вещество состоит из частиц - молекул, возникает очевидное желание получить описание его свойств в результате решения динамической задачи о движении всех частиц. Как  уже отмечалось, адекватное описание движения микроскопических частиц возможно лишь на языке вантовой механики. Однако в случаях, когда частицы оказываются почти свободными, описывающие их уравнения квантовой механики переходят в законы движения ньютона. Т.о. возникает принципиальная возможность получить правильное описание поведения вещества в газообразной форме, используя подходы классической физики. Реально подобная динамическая задача не может быть решена из-за фантастически большого числа частиц, образующих макроскопические порции вещества (например, в 1кг молекулярного водорода число молекул составляет 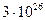, т.е. настолько огромно, что одна только проблема записи результатов расчета всех координат оказывается заведомо невыполнимой).

      Более плодотворным оказался феноменологический подход к созданию теории вещества, состоящий в введении новых термодинамических характеристик, удобных  для   описания макроскопических ансамблей   (массы, давления, температуры, объема и энтропии),  и  экспериментального исследования связей между ними. Основным результатом такого подхода была формулировка уравнения состояния идеального газа (уравнения Менделеева-Клайперона):

(1)         

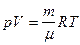
и уравнений теплового баланса, долгое время вполне удовлетворявших практическим потребностям теплофизики.

        Несмотря на успехи, описанный подход не мог считаться удовлетворительным, поскольку не соответствовал принципу экономии мышления и содержал новые величины и понятия, никак не связанные с уже имевшимися в фундаментальных теориях. В результате был разработан статистический подход, являющийся своеобразным компромиссом между  двумя рассмотренными. В его рамках ставится задача вычисления не набора динамических переменных всех частиц системы, а их средних значений. Эти средние сказываются тесно связанными с термодинамическими характеристиками вещества. Т.о. статистический подход позволяет установить более глубокий физический смысл феноменологически введенных термодинамических величин и объяснить природу связывающих их закономерностей.

      Распределение Максвелла. Первым удачным опытом реализации статистического подхода в теории вещества было решение задачи о распределении по скоростям молекул идеального газа (газа, расстояния между молекулами которого значительно превышают размеры молекул, и в котором притяжение молекул играет существенно меньшую роль, чем межмолекулярное отталкивание). Исходными предпосылками, позволившими решить задачу, были:

1.) Газ находится в состоянии термодинамического равновесия (т.е. его макроскопические параметры и средние значения микроскопических параметров не изменяются во времени).

2.) Все столкновения молекул происходят по законам упругого удара (т.е. при каждом столкновении выполняются законы сохранения импульса и механической энергии).

3.) Пространство, заполненное газом, является однородным и изотропным (это требование, например, предполагает отсутствие силы тяжести и каких-либо других внешних силовых полей).

4.) Молекулы обладают тремя степенями свободы (т.е. не способны вращаться и совершать колебаний).

5.) Движение молекул происходит независимо вдоль каждой из координатных осей.

     Перечисленные допущения позволили чисто математически (без каких-либо дополнительных физических требований) рассчитать функцию распределения молекул по скоростям f(v), с помощью которой вероятность обнаружения молекулы, составляющие вектора скорости которой лежат в интервалах

(1)       ,

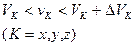вычисляется по формуле:

(2)        .

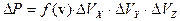     Найденное Максвеллом распределение имело вид:

(3)        .

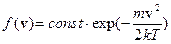Соответствующие графики при различных абсолютных температурах приведены на рис. 7_1, из которых видно, что при любых температурах наибольшая вероятность соответствует скоростям молекул, лежащим в области нуля. Увеличение температуры вызывает лишь относительное увеличение доли быстрых молекул. При T->0 распределение локализуется в раионе точки v=0, что означает исчезновение теплового движения молекул.

       Из полученного Максвеллом распределения (3) непосредственно следуют выражения, связывающие термодинамические величины (температуру и давление) с механическими (кинетическая энергия и концентрация частиц):

(4)        ,

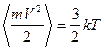(5)        .

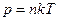Из уравнений молекулярно-кинетической теории (4) и (5), в свою очередь, следует уравнение состояния идеального газа (1) и объясняются все имперически - найденные газовые законы (например, увеличение давления при нагревании происходит из-за того, что появившаяся группа более быстрых молекул чаще ударяет о стенки сосуда и передает им при каждом ударе больший импульс).

     Разработанный Максвеллом подход позволил не только объяснить уже известные законы поведения газа, но и обобщить их на случаи, не описываемые уравнением состояния (1) (поведение газа в силовом поле и при концентрациях, когда приближение идеального газа становится неприменимым).

     Распределение Больцмана является естественным обобщением (3) на случай газа, находящегося под действием внешних сил. При их отсутствии (и, следовательно, равной нулю потенциальной энергии) экспоненциальный множитель содержал отношение кинетической и средней тепловой энергий. Учет наличия сил, очевидно, может быть осуществлен заменой (3) на

(6)        .

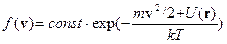Так, поскольку вблизи поверхности Земли потенциальная энергия молекулы с массо m равна U=mgh, из (6) следует, что вероятность найти молекулу на определенной высоте (а вместе с ней и плотность и давление газа) уменьшается по экспоненциальному закону:

(7)       

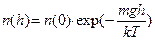
тем быстрее, чем больше масса молекул газа (рис. 7_2). На этом свойстве основаны многочисленные методы разделения смесей веществ с различными молекулярными весами (отстаивание и центрифугирование).

 

       Нестабильность атмосфер планет. Предсказываемый формулой (7) экспоненциально-быстрый спад до 0 концентрации газа на больших высотах (сравнимых с радиусом планеты) оказывается ошибочным из-за того, что в указанной области приближеной выражение для потенциальной энергии U=mgh становится неприменимым. Подстановка точного выражения

(8)       

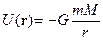
в (7) показывает, что даже при бесконечно-большом удалении от планеты концентрация газа не должна падать до нуля. Физически это означает, что газ из атмосфер планет должен перетекать в открытый космос до тех пор, пока там не установится конечное давление. Учитывая колоссальное различие объемов пустого космического пространства и атмосфер планет, из сказанного легко понять, что равновесные атмосферы у шарообразных космических тел невозможны. Скорость потери планетой ее атмосферы сильно зависит от ее температуры и массы: в космос улетают лишь те молекулы, чья скорость превосходит вторую космическую. Как видно из распределения Максвелла, вероятность обнаружить быструю молекулу весьма быстро спадает с увеличением скорости. Поэтому более массивные планеты (Земля, Венера) теряют свою атмосферу значительно медленнее, чем легкие (Марс, Луна).

        Молекулярно-кинетическая теория и “первое начало термодинамики”.  Молекулярно-кинетическая теория позволила дать простое объяснение так называемому первому началу термодинамики. Этот весьма общий закон первоначально был сформулирован в результате обобщения опыта многочисленных неудачных попыток создания вечного двигателя первого рода - весьма привлекательного с экономической точки зрения технического устройства, способного производить механическую работу, большую чем подведенная к нему тепловая (или другая) энергия. Одной из формулировок первого начала является утверждение о невозможности подобного устройства,  другой - закон сохранения энергии, записываемый в виде:

(9)        ,

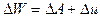где второе слагаемое описывает “невосполнимую потерю” части подведенной к устройству энергии.

     Согласно общему закону сохранения, энергия не исчезает, а переходит в другие формы. С точки зрения молекулярно-кинетической теории введенная в (9) дополнительная величина u (т.н. внутренней энергия)  имеет простой механический смысл и представляет собой сумму кинетических энергий теплового движения всех молекул и потенциальных энергий их взаимодействия. Т.о. часть подводимой к двигателю (или любой другой термодинамической системе) энергии тратится на ее нагревание.

       Применение статистического подхода в других областях естествознания. Впоследствии объединенное распределении Максвелла-Больцмана было получено из весьма общих соображений, справедливых не только для идеальных газов, но и для других равновесных статистических ансамблей, в которых вероятность нахождения объекта в рассматриваемом состоянии не зависит от числа уже имеющихся объектов в этом состоянии. Так распределения типа (6) часто встречаются в физике плазмы, физике растворов, в химии, имеется опыт их успешного применения в таких мало похожих на идеальный газ системах, как, например, не связанные с атомами электроны в проводящих кристаллах и даже электронные оболочки атомов с большими порядковыми номерами. Представляется весьма вероятным, что сходные подходы могут быть плодотворными и в других областях, где сложность рассматриваемых систем не позволяет производить точные расчеты поведения каждого отдельного элемента - биологии, экономике, социологии (например, автору известны не претендующие на большую серьезность попытки физиков вывести аналогичные максвелловским функции распределения людей по деньгам, городов по населению и т.п.).

                                        Раздел - 2

                        Мир глазами Альберта Эйнштейна

 

9. Электрический заряд и электромагнитные взаимодействия

       Электростатические взаимодействия. Как и другие фундаментальные понятия физики, понятие заряда не может быть строго определено. По существу заряженными мы называем тела, способные участвовать в электромагнитных взаимодействиях.  В общем случае эти взаимодействия достаточно сложны и зависят не только от взаимного расположения тел и их свойств, но и от скоростей движения. В простейшем случае, когда оба заряженных тела покоятся, взаимодействие между ними называются электростатическими. В случае точечных заряженных тел (т.е. тел, размеры которых малы по сравнению с расстоянием между ними) электростатические взаимодействия описываются законом Кулона:

     Сила, действующая между двумя точечными покоящимися зарядами обратно пропорциональна квадрату расстояния между ними и направленными вдоль прямой, соединяющие эти частицы:

(1)      .

Т.о. заряженными можно назвать такие тела, которые, находясь в покое, взаимодействуют с силой (1). Такая зависимость от расстояния отличает электростатические взаимодействия от ядерных, убывающих с расстоянием значительно быстрее.

     Гравитационные силы, как и электростатические, убывают обратно пропорционально квадрату расстояния. Имеются следующие принципиальные различия между этими силами:

1. Электростатические силы существенно превосходят гравитационные (например, электростатическое притяжение электрона к ядру атома превосходит гравитационные в 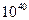 раз.

2. Электростатические силы могут быть как силами притяжения, так и отталкивания, в то время как гравитационные - только притяжения.

3.  Величина гравитационных сил пропорциональна массам взаимодействующих тел, что приводит к специфическому для гравитации явлению невесомости. Подобной зависимости от массы в электростатических силах не наблюдается.

     Электрический заряд. Как уже упоминалось, электростатические взаимодействия могут приводить к появлению сил притяжения и отталкивания. Опыт показывает, что все заряженные частицы можно разбить на две группы так, чтобы любая пара из одной группы отталкивалась, а из различных - притягивалась. Частицы, входящие в одну группу с электроном условно были названы отрицательными, в другую - положительными. Для количественной характеристики способности частиц участвовать в электростатических взаимодействиях была введения скалярная величина электрический заряд таким образом, чтобы возникающая сила оказывалась пропорциональной произведению взаимодействующих зарядов:

(2)  (2)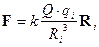  

(коэффициент пропорциональности в (2) зависит от выбора системы единиц). Введение знаков “+” и “-“ для различия двух типов зарядов оказалось весьма удобным, т.к. позволило описать притяжение и отталкивание при помощи одной математической формулы (2).

     Весьма примечательным является факт, что электрические заряды всех относительно стабильных заряженных элементарных частиц равны друг другу по модулю. Это позволило ввести понятие элементарного заряда (е). До настоящего времени не обнаружено способных существовать обособленно элементарных частиц с зарядом, не кратным элементарному (имеются основания полагать, что сами элементарные частицы “составлены” из “субчастиц” - кварков, заряды которых кратны e/3, однако до сих пор свободные кварки в экспериментах не обнаружены). Величина заряда любого макроскопического тела определяется разностью составляющих его положительных и отрицательных частиц и, разумеется, кратна элементарному заряду. Говорят, что электрический заряд дискретен.

     Существование элементарного заряда делает привлекательным выбор такой системы единиц, в которой он равнялся бы единице. Однако, по историческим причинам и  из соображений удобства ведения технических расчетов в качестве единицы заряда была выбрана другая, гораздо большая величина (единица заряда в системе Си превосходит элементарный в 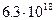 раз, в системе Гаусса заряд выбирается так, чтобы коэффициент в законе Кулона (2) равнялся 1).

     Другим свойством электрического заряда является абсолютно точно выполняемый закон его сохранения: в замкнутой системе алгебраическая сумма зарядов не изменяется во времени. Этот закон нетривиален, поскольку закона сохранения носителей зарядов (элементарных частиц) не существует: они могут превращаться друг в друга. Однако, при взаимопревращениях частиц суммарный заряд остается постоянным. Реакция типа

(3)  (3)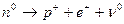  

невозможна. Отсутствие экспериментальных данных о существовании некоторых допускаемых законом сохранения электрического заряда реакций превращения элементарных частиц делает привлекательным введение новых типов зарядов (лептонный, странность, очарование и т.д.), и соответствующих им законов сохранения.

     Концепция поля.  Заряженные частицы взаимодействуют друг с другом на расстоянии в пустом пространстве. Возникает вопрос о механизме возникновения этих сил. Достаточно естественной выглядит полевая концепция, согласно которой каждый заряд создает вокруг себя в пространстве “нечто”, называемое электрическим полем,  а действующая на другой заряд сила возникает вследствие его взаимодействия с полем в той точке пространства, где он находится. Т.о. поле выступает в роли переносчика взаимодействия между заряженными частицами.

     В пользу объективного существования поля свидетельствуют следующие факты:

1.  Конечность скорости распространения изменения поля, вызванного изменением его источника.

2.  Наличие энергии в “пустом” пространстве, заполненным полем, которое в принципе может быть зарегистрировано не только при помощи электростатических взаимодействий.

3.  Возможность существования поля после исчезновения его источника.

     Введенная для электромагнитных взаимодействий, полевая концепция оказалась весьма удобной.  Она позволяет разбивать задачу о взаимодействии тел на две: расчет поля в точке расположения частицы и расчет силы, возникающей при ее взаимодействии с этим полем. В настоящее время понятие поля используется для описания всех типов фундаментальных взаимодействий.

     Электростатическое поле и его свойства. Электростатическое поле создается заряженными частицами. В случае нескольких частицы выполняется принцип суперпозиции: полное поле равно сумме полей, создаваемых каждым из источников. Количественной характеристикой электростатического поля является вектор напряженности Е, равный по определению силе, действующей со стороны поля на единичный заряд, помещенный в рассматриваемую точку пространства.

(4)    

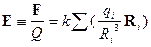
 Графически поле удобно изображать в виде силовых линий, кривых, в каждой точке которых вектор Е направлен по касательной. Величина напряженности определяется густотой линий. Линии вектора Е начинаются на положительных зарядах или на бесконечности, оканчиваются - на отрицательных или на бесконечности. Замкнутых линий электростатического поля не существует (рис. 9_1)

   Потенциал  электростатического поля.. Поля с перечисленными свойствами типа называются потенциальными, поскольку для помещенных в них тел может быть введено понятие потенциальной энергии как работы сил поля по перемещению заряда в точку, принятую за нулевую. При этом потенциальная энергия оказывается пропорциональной величине заряда помещенного в поле тела. Это позволяет ввести характеризующее только поле понятие потенциала как энергии единичного заряда в рассматриваемой точке:

(4)     ,

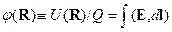где символ “( , )” использован для обозначения операции скалярного произведения векторов, определяемой равенством:

(5)       ;

в простейшем геометрическом представлении вектором в виде стрелок скалярное произведение числено равно произведению длин векторов на косинус угла между ними.

     Потенциал в системе единиц Си измеряется в вольтах . Человек способен ощущать разность потенциалов около 1В. Напряжение (разность потенциалов), превосходящее 30В, считается опасным для жизни.

     Движение частиц в электростатических полях.  Электрические силы (F=QE), направленные вдоль поля (в случае положительно заряженных частиц) и против (в случае отрицательных),  способны изменять скорость зарядов как по величине, так и по направлению. Это обуславливает широкое использование электростатических полей для разгона и управления движением заряженных частиц. Так в электронно-лучевых трубках телевизоров и осциллографов электроны создаются и разгоняются в заряженном до разности потенциалов ок.30кВ конденсаторе - электронной пушке и посылаются в нужную точку флюоресцирующего при их ударах ударах экрана при помощи изменяемых во времени полей в конденсаторах, образующих отклоняющую систему (рис. 9_2).

     Магнитные взаимодействия.  Опыт показывает, что силы, возникающие между зарядами при их движении, отличаются от электростатических. Для описания возникающих отличий был введен новый тип взаимодействий - магнитные и их переносчик - магнитное поле. Для количественного магнитных полей был введен вектор магнитной индукции В так, чтобы действующая на движущейся со скоростью v  заряд Q сила вычислялась по формуле:

(6)      ,

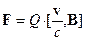где символ “[ , ]” использован для обозначения операции векторного умножения, определяемой в трехмерном случае соотношением:

(7)      

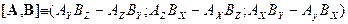
и представляет собой вектор, числено равный площади параллелограмма, построенного на перемножаемых векторах, и направленный перпендикулярно его плоскости в стороны, определяемую по правилу правой руки (рис. 9_3).

     Магнитное поле и его свойства. Магнитные поля создаются движущимися зарядами, подчиняются принципу суперпозиции и могут быть рассчитаны согласно:

(8)      .

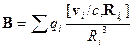Обычно магнитные поля изображают с помощью линий, в каждой точке которых вектор В направлен по касательной. В случае движущегося равномерно и прямолинейно заряда линии В представляют собой семейство окружностей с центрами, лежащими на его траектории (рис. 9_4). В общем случае линии магнитного поля представляют собой замкнутые кривые, нигде не возникающие и не обрывающиеся. Поля с такими свойствами называют вихревыми.

     Движение заряженных частиц в магнитных полях в общем случае происходит по винтовым траектория, “накрученным” на линии В (рис.9_4). Радиус кривизны траектории (при заданном поле) определяется перпендикулярной полю составляющей начальной скорости и удельным зарядом частицы (q/m), период вращения определяется только удельным зарядом, шаг траектории - направленной по полю составляющей скорости. При движении в магнитном поле кинетическая энергия частиц не меняется, действующие силы вызывают лишь изменения направления движения. Магнитные поля широко используются для управления пучками заряженных частиц (магнитная фокусировка в электронно-лучевых трубках), их сортировке по скоростям (монокинетизации электронных пучков) или удельным зарядам (масс-спектроскопия, пузырьковые камеры в магнитных полях и т.д.).

     Магнитное поле Земли предохраняет биосферы от попадания опасных для жизни потоков заряженных частиц, приходящих из космоса. Эти частицы, закручиваясь вокруг линий В, “путешествуют” от одного магнитного полюса планеты к другому за среднее время порядка. 1.5 с.

      Электрические и магнитные поля в веществе. С точки зрения теории электричества вещество при нормальных условиях можно рассматривать как вакуум с относительно небольшим количеством связанных зарядов и молекулярных токов. Первые представляют собой главным образом совокупности положительно заряженных ядер и окружающих их отрицательно заряженных электронных облаков; вторые - обусловлены движением электронов в атомах и специфическим (присущим микрообъектам) внутренним движением - спином. Полные электрическое и магнитное поля в веществе является суперпозицией внешних полей (создаваемых “свободными” зарядами и токами) и полей, создаваемых зарядами вещества. При отсутствии внешнего поля заряды и токи в веществе обычно распределяются так, что их средние электрическое и магнитное поля оказываются равными нулю. Внешние поля вызывают перераспределение  связанных зарядов и молекулярных токов и, как следствие, появление дополнительных полей в веществе.

      В большинстве веществ (диэлектрика) отрицательно заряженные электроны достаточно крепко связаны  электрическими силами с положительными ядрами, и внешнее поле не способно привести к значительному перераспределению зарядов. В таких веществах электрическое поле оказывается меньшим по сравнению с полем, которое создавали бы свободные заряды в вакууме. В металлах электроны способны практически беспрепятственно перемещаться и под действием электрического поля двигаются до тех пор, пока не создадут в веществе конфигурации, при которой полное поле обратится в 0. В диэлектриках электрическое поле ослабевает, в металлах равно 0.

     По отношению к реакции на внешнее магнитное поле вещества подразделяются на диамагнетики (ослабляют магнитное поле), парамагнетики (поле в веществе незначительно увеличивается) и ферромагнетики (поле возрастает в десятки тысяч раз и не исчезает после выключения внешнего поля). В отличие от электростатики, непротиворечивая теория магнитных свойств вещества может быть изложена лишь на языке квантовой механики.

Кафедра “Название кафедры”	Утверждаю Ректор ИМИСП _______________  А.Н.Лапин "____" ____________ 199__

 

Учебная программа

по дисциплине

"Современные концепции естествознания"

для студентов программы	"Бакалавр Менеджмента"
направление подготовки	521500, Менеджмент

 

 

	Курс	Семестр	Вид(ы) заключительного контроля
Современные концепции естествознания	1	2	зачет

 

 

название дисциплины:  Современные концепции естествознания

Цели и задачи:  на базе фактических сведений, полученных при изучении курсов в рамках СРЕДНЕ ОБРАЗОВАТЕЛЬНОЙ программы сформировать  у  обучаемых  правильные философско-мировоззренческие ПРЕДСТАВЛЕНИЯ о взглядах современного естествознания на устройство окружающего мира, основных перспективных НАПРАВЛЕНИЯХ дальнейшего развития естественно научных дисциплин, их месте в современной системе общечело\-веческих ценностей и возможностях их практического применения.

 

Методика преподавания:  проведение обзорных лекций-дискуссий после обязательного первоначального ознакомления учащихся с темой очередного занятия по авторскому конспекту; выбор выносимых на обсуж\-дение тем осуществляется с учетом пожеланий учащихся; в случае наиболее ТРУДНО ВОСПРИНИМАЕМЫХ тем лекция сопровождается компьютерными демон\-страциями изучаемых моделей.

Структура дисциплины (час.)

 

		Аудиторные занятия	Самостоятельная работа
№	Тема	Лекции	Семинары, деловые игры, лабораторные работы	студентов
1      1	Введение	2	0
2      2	Мир глазами Исаака Ньютона	4	4
3      3	Мир глазами Альберта Эйнштейна	4	2
4      4	Мир глазами Нильса Бора	4	4
5      5	Мир глазами Поля Дирака	4	2
6      6	Заключение	2	0
	ИТОГО:	20	12	сумма
	ВСЕГО:	32

 

 

 

Содержание дисциплины

Введение. Структура естественно научных знаний и их роль в развитии общества.

1.    1.    Мир глазами Исаака Ньютона: обзор основных достижений классического естествознания. (Классические представления о пространстве и времени. Способы описания движения. Взаимодействия. Законы сохранения и их связь с симметрией систем. Строение солнечной системы. Статистическое описание равновесных систем. Неравновесные системы и самоорганизация. Биологическая эволюция.)

2.    2.    Мир глазами Альберта Эйнштейна: Теория относительности - как первый опыт критического переосмысления классических концепций естествознания. (Электромагнитные взаимодействия и концепция поля. Необходимость переосмысления классических представлений о пространстве-времени. Принцип соответствия. Основные выводы специальной теории относительности. Гравитация и современные взгляды на строение Вселенной. Энергетика и экология.)

3.    3.    Мир глазами Нильса Бора: квантовомеханический способ описания и отказ от требований классического детерминизма. (Физические и психологические аспекты зрительного восприятия образов. Традиционное описание оптических явлений - первый шаг к волновой механике. Фотоны и кванты. Философские аспекты проблемы познаваемости мира в свете корпускулярно-волнового дуализма и соотношения неопределенности. Вероятностное описание событий. Химические процессы с точки зрения квантовомеханического описания. Проблема нарушения четности . )

4.    4.    Мир глазами Поля Дирака: квантовая электродинамика как попытка синтеза идей релятивизма и квантовомеханического подхода к описанию объектов микромира. (Спин как пример не имеющего классического аналога свойства реальных объектов. Квантовая статистика: бозоны и фермионы. Современные лазеры и их использование. Строение атомов и кристаллов. Полупроводники и их использование. Понятие об архитекруре ЭВМ. Дираковский вакуум, частицы и античастицы.  Фотоны и колебания вакуума. Нанотехнологии.)

5.    5.    Заключение. Естественно научные теории: создание, проверка, развитие, использование, замена более совершенной.

Общие замечания по содержанию дисциплины

      В настоящем курсе не ставится задача систематического описания окружающего мира с точки зрения современного естествознания, что, очевидно, невозможно в рамках односеместрового курса, и  весьма проблематично для естественно научных факультетов университетов. По убеждению автора в курсе “Современные концепции естествознания” для студентов экономических специальностей основное внимание должно уделяться следующим аспектам:

1. Объективное существование законов природы, независящих от определяемых мировоззрением исследователя его желаний и часто невписывающихся в ранее общепринятые теоретические концепции.

2.  Сложность адекватного прогноза коммерческой реализации новой естественно научной теории на ранних этапах ее развития.

3.  Необходимость математизации естественно научных теорий в целях ускорения их развития и облегчения общения между представителями смежных  наук.

Литература

            Основная

1. А.Г.Спирин "Основы философии", М., 1988.

2. В.П.Бранский "Философское значение "проблемы наглядности" в

   физике", Л., 1962.

3. Л.Купер "Физика для всех", Наука, М., 1980, т.1,2.

4. Р.Фейнман "Характер физических законов", М., 1970.

 

            Дополнительная

5. И.Р.Пригожин "От существующего к возникающему", М., 1994.

6. Ю.Л.Ермолаев, А.Л.Сание "Электронная синергетика", ЛГУ, 1989.

7. Ю.Л.Климонтович "Турбулентное движение и структура хаоса",

   Наука,1990.

8. А.П.Пурмаль "Как превращаются вещества", Наука,1989.

9. М.Д.Франк-Каменецкий "Самая главная молекула", Наука, 1989.

10.М.Б.Веркимблит "Электричество в живых организмах", Н.,1989.

11. И.Д.Новиков “Как взорвалась Вселенная”, Н.,1990.

12. К.Ю.Богданов “Физик в гостях у биолога”. Н., 1990.

13. А.В.Бялко “Наша планета Земля”. Н. 1990.

Составитель:  

чирцов  александр сергеевич,

                                                                    кандидат физ.-мат. наук,

                                                                   доцент физического факультета  сПбГУ