Содержание
ВВЕДЕНИЕ. 3
1. Характеристика методов выявления тенденции в
рядах динамики. 5
1.1. Метод укрупнения интервала динамического ряда. 6
1.2. Метод скользящей средней. 7
1.3. Метод аналитического выравнивания. 9
1.4. Метод конечных разностей. 11
1.5. Методы адаптивного моделирования и
прогнозирования. 17
2. Технология выявления тенденции методом
аналитического выравнивания по прямой. 22
ЗАКЛЮЧЕНИЕ. 27
СПИСОК ЛИТЕРАТУРЫ.. 28
ВВЕДЕНИЕ
Статистика – особая отрасль практической
деятельности людей, направленная на сбор, обработку и анализ данных,
характеризующих социально-экономическое развитие страны, ее регионов, отраслей
экономики, отдельных предприятий. Статистикой также называют науку,
занимающуюся разработкой теоретических положений и методов, используемых
статистической практикой хозяйственных субъектов экономики. Между
статистической наукой и практикой существует тесная связь. Статистическая
практика применяет методы, выработанные наукой; в свою очередь статистическая
наука опирается на материалы практики и, обобщая опыт практики, разрабатывает
новые правила обработки информации.
Особенность
статистики заключается в том, что
статистические данные сообщаются в количественной форме, т.е. статистика
говорит языком цифр, отображающих общественную жизнь во всем многообразии ее
проявлений. При этом статистику прежде всего интересуют те выводы, которые
можно сделать на основе анализа надлежащим образом собранных и обработанных
цифровых данных.
Одной
из важнейших задач статистики является изучение изменений анализируемых
показателей во времени. Эти изменения можно изучать, если иметь данные по
определенному кругу показателей на ряд моментов времени или за ряд промежутков
времени, следующих друг за другом. Таким образом временные ряды (динамические)
являются важным инструментом статистического анализа, что обусловливает
актуальность выбранной темы.
Цель
работы – характеристика методов выявления тенденции в рядах динамики, а также
иллюстрация их практического применения на примере деятельности строительного
концерна «Сибирь».
Поставленная цель требует постановки и решения
следующих задач:
-
характеристика основных методов выявления тенденции в
рядах динамики;
-
сравнение методов
выявления тенденции в рядах динамики;
-
ранжирование методов по степени их сложности и
применимости в анализе временных рядов;
-
подробная характеристика метода аналитического
выравнивания на примере основных показателей коммерческой деятельности строительного
концерна «Сибирь».
1. Характеристика методов выявления тенденции в
рядах динамики
Одной из задач, возникающих при анализе рядов
динамики, является установление закономерности изменения уровней изучаемого
показателя во времени.
В некоторых случаях эта закономерность, общая
тенденция развития объекта вполне ясно отображается уровнями динамического
ряда. Так, в приведенном в табл.1 примере уровнями динамического ряда
свойственна тенденция к снижению, не нарушаемая на протяжении всего
рассматриваемого периода. В других рядах динамики наблюдается систематическое
увеличение уровней ряда (например, при изучении динамики средней заработной
платы по данным табл.2. Однако часто приходится встречаться с такими рядами
динамики, когда уровня ряда претерпевают самые различные изменения (то
возрастают, то убывают) и можно говорить лишь об общей тенденции развития
явления, либо о тенденции к росту, либо к снижению. В этих случаях для
определения основной тенденции развития явления, достаточно устойчивой на
протяжении данного периода, используют особые приемы обработки рядов динамики
на примере основных производственных показателей деятельности строительного
концерна «Сибирь» [12].
Таблица 1
|
Годы
|
Всего
построено (млн.кв.м) жилищно-строительными коопера-тивами
|
Абсолютное изменение млн.
кв.м
|
Коэффициенты роста по
сравнению
|
Темпы прироста (%) по
сравнению
|
|
по сравне-нию с уровнем 1999
г.
|
по сравне-нию с предшес.
годом
|
с 1999 г.
|
с предшествующим
годом
|
с 1999 г.
|
с предшествующим
годом
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
1999
|
2,9
|
-
|
-
|
-
|
-
|
-
|
-
|
|
2000
|
2,4
|
-0,5
|
-0,5
|
0,8276
|
0,8276
|
-17,24
|
-17,24
|
|
2001
|
2,1
|
-0,8
|
-0,3
|
0,7241
|
0,8750
|
-12,50
|
-12,50
|
|
2002
|
1,9
|
-1,0
|
-0,2
|
0,6552
|
0,9048
|
-9,52
|
-9,52
|
|
2003
|
1,8
|
-1,1
|
-0,1
|
0,6207
|
0,9474
|
-5,26
|
-5,26
|
Уровня
ряда динамики формируются под совокупным влиянием множества длительно и
кратковременно действующих факторов и в том числе различного рода случайных
обстоятельств. Выявление основной закономерности изменения уровней ряда
предполагает ее количественное выражение, в некоторой мере свободное от
случайных воздействий. Выявление
основной тенденции развития (тренда) называется в статистике также выравниванием
временного ряда, а методы выявления основной тенденции – методами выравнивания [7,
с. 31]. Выравнивание позволяет
характеризовать особенность изменения во времени данного динамического ряда в
наиболее общем виде как функцию времени, предполагая, что через время можно
выразить влияние всех основных факторов.
Таблица 2
|
Месяцы
|
Среднемесячная заработная
плата
|
|
тыс. руб.
|
|
Январь
2003
|
302,6
|
|
Февраль
2003
|
321,0
|
|
Март
2003
|
361,5
|
|
Апрель
2003
|
386,2
|
|
Май
2003
|
429,9
|
|
Июнь
2003
|
480,6
|
|
Июль
2003
|
499,5
|
1.1. Метод укрупнения интервала динамического ряда
Один
из наиболее простых приемов обнаружения общей тенденции развития явления – укрупнение интервала динамического ряда [6,
с. 45]. Смысл приема заключается в том, что первоначальный ряд динамики
преобразуется и заменяется другим, показатели которого относятся у большим по
продолжительности периодам времени. Например, ряд, содержащий данные о месячном
объеме производства может быть преобразован в ряд квартальных данных. Вновь
образованный ряд может содержать либо абсолютные величины за укрупненные по
продолжительности промежутки времени (эти величины получают путем простого
суммирования уровней первоначального ряда
абсолютных величин), либо средние величины. При суммировании уровней или
при выведении средних по укрупненным интервалам отклонения в уровнях, обусловленные
случайными причинами, взаимопогашаются, сглаживаются и более четко обнаруживается
действие основных факторов изменения уровней
(общая тенденция).
1.2. Метод скользящей средней
Выявление
основной тенденции может быть осуществлено также методом скользящей средней [3, с. 132]. Для определения скользящей
средней формируем укрупненные интервалы, состоящие из одинакового числа
уровней. Каждый последующий интервал получаем, постепенно сдвигаясь от
начального уровня динамического ряда на один уровень. Тогда первый интервал
будет включать уровни y1, y2, …, ym; второй –
уровни y2, y3, …, ym+1 и т.д.
Таким образом, интервал сглаживания как бы скользит по динамическому ряду с
шагом, равным единице. По сформированным укрупненным интервалам определяем
сумму значений уровней, на основе
которых
рассчитываем скользящие средние. Полученная средняя относится к середине
укрупненного интервала. Поэтому при сглаживании скользящей средней технически
удобнее укрупненный интервал составлять из нечетного числа уровней ряда.
Нахождение скользящей средней по четному числу уровней создает неудобство,
вызываемое тем, что средняя может быть отнесена только к середине между двумя
датами. В этом случае необходима дополнительная процедура центрирования
средних. Ниже приводится порядок расчета скользящих средних, используя данные о
дневном выпуске продукции предприятия за месяц (табл.3).
Возьмем
в качестве укрупненного интервала период в 3 дня, тогда первая скользящая сумма
будет равна объему производства за первый, второй и третий рабочий дни, вторая
скользящая сумма – за второй, третий и четвертый рабочие дни и т.д. В табл. 3 в
гр.3 и 4 приведены скользящие суммы за трехдневный и пятидневный промежутки.
Скользящая средняя, рассчитанная по трехдневным
скользящим суммам будет отнесена ко второму дню каждой трех дневки
(см.гр.5). Скользящая же средняя, рассчитанная по пятидневным суммам (см.гр.6),
относится к третьему дню соответствующей пятидневки [12].
Таблица 3
|
Рабочие дни месяца
|
Выпуск продукции, млн.
руб.
|
Скользящие суммы,
млн. руб.
|
Скользящие средние,
млн. руб.
|
|
3-х дневные
|
5-ти дневные
|
3-х дневные
|
5-ти дневные
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
37
|
-
|
-
|
-
|
-
|
|
2
|
42
|
112
|
-
|
37,3
|
-
|
|
3
|
33
|
120
|
215
|
40,0
|
43,0
|
|
4
|
45
|
136
|
233
|
45,3
|
46,6
|
|
5
|
48
|
158
|
247
|
52,7
|
49,4
|
|
6
|
55
|
169
|
284
|
65,3
|
56,8
|
|
7
|
56
|
181
|
308
|
60,3
|
61,6
|
|
8
|
70
|
195
|
324
|
65,0
|
64,8
|
|
9
|
69
|
213
|
324
|
71,0
|
64,0
|
|
10
|
74
|
214
|
340
|
71,3
|
68,0
|
|
11
|
71
|
231
|
370
|
77,0
|
74,0
|
|
12
|
86
|
227
|
370
|
75,7
|
74,0
|
|
13
|
70
|
248
|
393
|
82,7
|
78,6
|
|
14
|
92
|
230
|
387
|
76,7
|
77,4
|
|
15
|
68
|
253
|
404
|
84,3
|
80,8
|
|
16
|
93
|
242
|
423
|
80,7
|
84,6
|
|
17
|
81
|
263
|
425
|
87,7
|
85,0
|
|
18
|
89
|
264
|
460
|
88,0
|
92,0
|
|
19
|
94
|
286
|
476
|
95,3
|
95,2
|
|
20
|
103
|
306
|
494
|
102,0
|
98,8
|
|
21
|
109
|
311
|
516
|
103,7
|
103,3
|
|
22
|
99
|
319
|
-
|
106,3
|
-
|
|
23
|
111
|
-
|
-
|
-
|
-
|
Охарактеризуем
подход к выбору интервала сглаживания. Нередко выбор интервала сглаживания
осуществляется произвольно, однако при этом нужно учитывать количество уровней
в анализируемом ряду динамики, так как при использовании приема скользящей
средней сглаженный ряд сокращается по сравнению с исходным рядом на число уровней, равное (m-1). Вместе с тем, чем продолжительнее интервал
сглаживания, тем сильнее усреднение, а потому выявляемая тенденция развития
получается более плавной. Чаще всего интервал сглаживания может состоять из
трех, пяти или семи уровней. Первоначальные и выровненные динамические ряды с
помощью скользящих средних изображены на рис.1.

1.3. Метод аналитического выравнивания
Изучение
основной тенденции развития методом скользящей средней является лишь
эмпирическим приемом предварительного анализа. Рассмотренные приемы сглаживания
динамических рядов (укрупнение интервала и метод скользящей средней) могут
рассматриваться как важное вспомогательное средство, облегчающее применение
других методов и, в частности, более строгих методов выявления тенденции. Для
того чтобы представить количественную модель, выражающую общую тенденцию
изменений уровней динамического ряда во времени, используется аналитическое выравнивание ряда динамики [4,
с. 187]. В этом случае фактические уровни заменяются уровнями, вычисленными на
основе определенной кривой. Предполагается, что она отражает общую тенденцию
изменения во времени изучаемого показателя.
Таблица 4
|
Название функции
|
Описание
функции
|
|
1.Линейная
2. Парабола
второго порядка
3.
Кубическая парабола
4.
Показательная
5.
Экспоненциальная
6.
Модифицированная экспонента
7. Кривая
Гомперца
8.
Логистическая кривая
9.
Логарифмическая парабола
10.
Гиперболическая
|
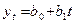
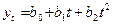
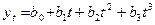
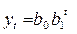
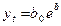
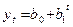
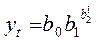
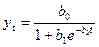


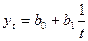
|
При
аналитическом выравнивании ряда динамики закономерно изменяющийся уровень
изучаемого показателя оценивается как функция времени 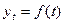 , где
, где 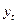 - уровни динамического ряда, вычисленные по соответствующему
аналитическому уравнению на момент времени t.В табл.4 приводятся различные виды трендовых моделей,
наиболее часто используемые для аналитического выравнивания [4, с. 176].
- уровни динамического ряда, вычисленные по соответствующему
аналитическому уравнению на момент времени t.В табл.4 приводятся различные виды трендовых моделей,
наиболее часто используемые для аналитического выравнивания [4, с. 176].
Выбор
формы кривой во многом определяет результаты экстраполяции тренда. Основанием
для выбора вида кривой может использоваться содержательный анализ сущности
развития данного явления. Можно опираться также на результаты предыдущих
исследований в данной области.
На
практике для этих целей прибегают к анализу графического изображения уровней
динамического ряда (линейной диаграммы). Однако из графического представления
эмпирических данных не всегда удается произвести однозначный выбор формы
уравнения. Поэтому целесообразно воспользоваться графическим изображением
сглаженных уровней, в которых случайные и волнообразные колебания в некоторой
степени оказываются погашенными (см. рис.1).
1.4. Метод конечных разностей
При
выборе вида кривой для выравнивания динамического ряда возможно также
использование метода конечных разностей,
который основан на свойствах различных кривых, применяемых при выравнивании
[2, с. 134]. Обязательным условием при этом является равенство интервалов между
уровнями динамического ряда.
Свойства
конечных разностей заключаются в следующем:
1.
Если общая тенденция выражается линейным уравнением
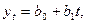
тогда
получаем
постоянными
первые разности: 
нулевыми
вторые разности:  .
.
Равенство
 постоянной величине и
постоянной величине и 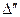 нулю при вычислении их
по фактическим данным рассматривается не для каждого отдельного случая, а лишь
в целом по всей совокупности уровней. Так, при
нулю при вычислении их
по фактическим данным рассматривается не для каждого отдельного случая, а лишь
в целом по всей совокупности уровней. Так, при
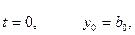
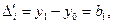
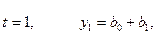
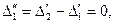
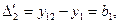
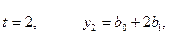

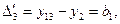

2.
Если тенденция выражается параболой второго порядка  то получим постоянными
– вторые разности, нулевыми – третьи разности.
то получим постоянными
– вторые разности, нулевыми – третьи разности.
Если
рассмотреть уравнение параболы при разных t, то получатся при:
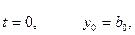
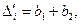
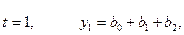
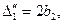
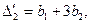
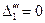
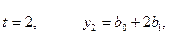


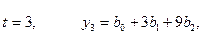
и
т.д.
Основываясь
на указанных свойствах конечных разностей для различных видов кривых, Е.М.
Четыркин сделал вывод о применимости для
выравнивания линейной функции, если любые три равностоящие уровня имеют нулевую
вторую разность [11, с. 156-157]. Порядок разностей, остающихся примерно равными
друг другу, принимается за степень выравнивающего многочлена, т.е. если
примерно одну и ту же величину имеют вторые разности, то для выравнивания используется
парабола второго порядка.
Можно
указать и ряд других признаков, которые могут помочь при выборе формы кривой:
если примерно постоянными оказываются темпы роста, то для выравнивания
применяется показательная функция; если первые разности имеют тенденцию
уменьшатся с постоянным темпом, то следует остановиться на модифицированной
экспоненте; если средние уровни, нанесенные на полулогарифмическую сетку,
близки к прямой линии, то предпочтительнее простая экспонента; если первые
разности обратных значений средних уровней изменяются на один и тот же процент,
то следует остановиться на логистической кривой.
При
выборе формы уравнения следует исходить и из объема имеющейся информации. Чем
больше параметров содержит уравнение тренда, тем больше должно быть наблюдений
при одной и той же степени надежности оценивания. Выбор формы кривой может
осуществляться и на основе принятого критерия, в качестве которого может
служить сумма квадратов отклонений фактических значений от значений,
рассчитанных по уравнению тренда. Из совокупности кривых выбирается та, которой
соответствует минимальное значение критерия.
Рассмотрим
аналитическое выравнивание ряда динамики по прямой, то есть аналитическое
уравнение вида:
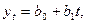
где t – порядковый номер периодов или моментов времени.
Параметры
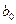 и
и  прямой рассчитываются
по методу наименьших квадратов (МНК)
[10, с. 87-88]. Система нормальных
уравнений в данном случае имеет вид:
прямой рассчитываются
по методу наименьших квадратов (МНК)
[10, с. 87-88]. Система нормальных
уравнений в данном случае имеет вид:
 .
.
Поиск
параметров уравнения можно упростить, если отсчет времени производить так, чтобы
сумма показателей времени изучаемого ряда динамики была равна нулю 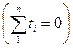 . При нечетном числе уровней ряда динамики для получения
. При нечетном числе уровней ряда динамики для получения 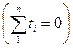 уровень, находящийся в
середине ряда, принимается за условное начало отсчета времени (этому периоду
или моменту времени придается нулевое значение). Даты времени, стоящие выше
этого уровня, обозначаются натуральными числами со знаком мину (-1, -2, -3 и
т.д.), а ниже – натуральными числами со знаком плюс (+1, +2, +3 и т.д.) (см.
гр.3 табл. 5).
уровень, находящийся в
середине ряда, принимается за условное начало отсчета времени (этому периоду
или моменту времени придается нулевое значение). Даты времени, стоящие выше
этого уровня, обозначаются натуральными числами со знаком мину (-1, -2, -3 и
т.д.), а ниже – натуральными числами со знаком плюс (+1, +2, +3 и т.д.) (см.
гр.3 табл. 5).
Если
число уровней динамического ряда четкое, периоды времени верхней половины ряда
(до середины) нумеруются –1, -3, -5 и т.д., а нижней - +1, +3, +5 и т.д. При
этому условии  будет равна нулю и
система нормальных уравнений преобразуется следующим образом:
будет равна нулю и
система нормальных уравнений преобразуется следующим образом:
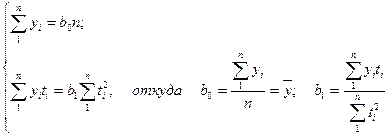
Если в изменениях уровней
обнаруживается тенденция к постоянству темпов роста, то выравнивание ряда
следует проводить по показательной кривой:
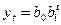 ,
,
где  – коэффициент роста.
– коэффициент роста.
Техника выравнивания по
показательной кривой аналогична технике выравнивания по прямой, за исключением
того, что выравниваются здесь не уровни ряда, а их логарифмы:
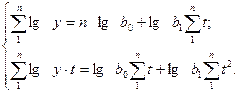
Приравнивая 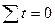 , получаем
, получаем
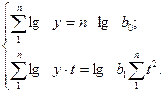 (8)
(8)
По вычисленным значения
логарифмов определяем величины параметров уравнения показательной кривой 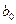 и
и  .
.
Современные компьютерные
программы по анализу временных рядов позволяют автоматически определять тип
модели, адекватной исходным данным, на основе соответствующего критерия.
Аналитическое уравнение
представляет собой математическую модель развития явления и дает выражение
статистической закономерности, проявляющейся в рядах динамики. Следует помнить,
что прием аналитического выравнивания содержит в себе ряд условностей,
связанных прежде всего с тем, что уровни, характеризующие тот или иной
динамический ряд, рассматриваются как функция времени. В действительности же
развитие явлений обусловлено не тем, сколько времени прошло с отправного
момента, а тем, какие факторы влияли на развитие, в каком направлении и с какой
интенсивностью. Развитие явлений во времени выступает как внешнее выражение
этих факторов, как их суммарное действие, оказывающее выражение этих факторов,
как их суммарное действие, оказывающее влияние на изменение уровня в отдельно
взятые промежутки или моменты времени. Выявить основную тенденцию развития явления
методом наименьших квадратов можно лишь тогда, когда выяснено, что
изменяющиеся во времени процессы протек5ают
на всем рассматриваемом промежутке времени одинаково, что их количественное и
качественное изменение происходит под действием одного и того же комплекса
основных факторов, определяющих движение данного ряда динамики.
Модели, учитывающие общие
закономерности изменения экономического явления в изучаемый интервал времени и
изменения во времени влияния комплекса факторов, называют многофакторными динамическими моделями [1, с. 81].
Допустим, что величина
исследуемого показателя 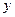 зависит от изменения
нескольких факторов
зависит от изменения
нескольких факторов  . Располагая данными по некоторой совокупности объектов за
ряд лет, можно построить корреляционную модель, характеризующую зависимость
. Располагая данными по некоторой совокупности объектов за
ряд лет, можно построить корреляционную модель, характеризующую зависимость 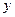 от указанных факторов
для каждого периода времени.
от указанных факторов
для каждого периода времени.
Предположим, что зависимость
может быть представлена линейной функцией. Тогда модель будет иметь вид:
для периода 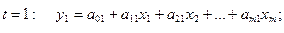
для периода 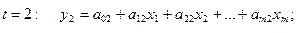
для периода 
и т.д.
Для всех периодов получим
систему из 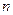 уравнений, и для
каждого из факторов будет
уравнений, и для
каждого из факторов будет 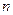 коэффициентов
регрессии, то есть будем иметь временные ряды для каждого из коэффициентов
регрессии:
коэффициентов
регрессии, то есть будем иметь временные ряды для каждого из коэффициентов
регрессии:
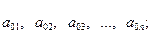
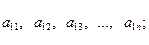
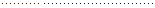

Рассматривая каждый из этих
временных рядов, можно представить  как функцию времени и,
используя аналитическое выравнивание, построить прогнозы коэффициентов
регрессии на период времени
как функцию времени и,
используя аналитическое выравнивание, построить прогнозы коэффициентов
регрессии на период времени 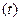 , то есть определить значение величин
, то есть определить значение величин 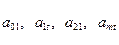
Тогда величина признака 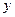 на период
на период  может быть представлена так:
может быть представлена так:
 .
.
Значения факторов 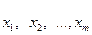 необходимо определить
также на момент времени
необходимо определить
также на момент времени  . Обычно для этого используют либо контрольные цифры, либо
экстраполяцию по линии тренда.
. Обычно для этого используют либо контрольные цифры, либо
экстраполяцию по линии тренда.
Еще раз следует подчеркнуть,
что прогноз уровня, характеризующего определенный объект с опорой на метод
аналитического выравнивания, основан на предположении, что те же самые условия,
в которых формировались уровни ряда в прошлом, будут существовать и в будущем.
Использование экстраполяции в изменившихся условиях, появление новых факторов,
оказывающих влияние на формирование уровней временного ярда, будет сопряжено с
более или менее значительными ошибками. Причем экстраполяция на отдаленные даты
подвержена более значительным ошибкам, чем краткосрочная экстраполяция. Это в
известной степени может объясняться определенной инерционностью развития
управляемых объектов: чем выше уровень управления, тем более инерционен объект
управления. Однако с удалением периода прогноза от фактических уровней
временного ряда влияние инерционности развития снижается и возрастает влияние
новых условий и факторов. Поэтому целесообразно постоянно обновлять временные
ряды по мере получения новых данных, что обусловливает и корректировку уравнений
тренда.
Выделим особенности моделей аналитического
выравнивания уровней динамического ряда, накладывающие ограничения на их
использование. Во-первых, динамические ряды, к которым применяется
аппроксимация, должны быть достаточно длинными. Во-вторых, применение
аппроксимации наиболее целесообразно в случае медленно и плавно меняющегося
уровня. В-третьих, аппроксимация как метод моделирования практически не
адаптируется к изменяющимся условиям формирования уровней ряда; при появлении
новых данных построение модели должно быть проведено заново. В-четвертых, при использовании
для расчета параметров уравнения метода наименьших квадратов считается, что
значимость информации в пределах отрезка аппроксимации одинакова независимо от
давности полученных данных, в то время как более поздние данные имеют большую
ценность.
1.5. Методы адаптивного моделирования и
прогнозирования
Помимо этого, динамические
ряды экономических показателей часто имеют небольшие длину и подвержены
значительным колебаниями, которые аппроксимация предвидеть не может. Поэтому в
практике статистического анализа экономических процессов большое
распространение получили методы
адаптивного моделирования и прогнозирования.
В основе адаптивных методов
лежит модель экспоненциального сглаживания, возможность использования которой
для прогнозирования была доказана Р.Брауном. Сущность этого метода заключается
в том, что временной ряд сглаживается с помощью взвешенной скользящей средней,
в которой веса распределяются по экспоненциальному закону. Такая взвешенная
скользящая средняя характеризует значения динамического ряда в конце интервала
сглаживания, то есть является характеристикой последних уровней ряда.
Экспоненциальная средняя
первого порядка для исходного рада записывается следующим образом:
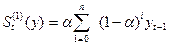 .
.
где  – экспоненциальная средняя первого порядка;
– экспоненциальная средняя первого порядка;
 - коэффициент
сглаживания.
- коэффициент
сглаживания.
Экспоненциальная средняя  –го порядка, соответственно определяется следующим образом:
–го порядка, соответственно определяется следующим образом:
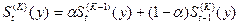
Коэффициенты полиномов,
используемых для прогнозирования, могут быть получены через сглаженные значения
ряда, и для линейной модели их формулы имеют следующий вид:

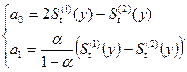
Рассмотрим последовательность
построения линейной модели на основе данных об объеме производства
строительного концерна «Сибирь» в 2003 г. (табл.7).
Начальные величины 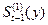 и
и 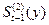 могут быть получены исходя из системы уравнений
могут быть получены исходя из системы уравнений
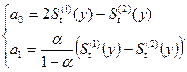
подстановкой параметров 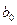 и
и  , полученных при выравнивании динамического ряда по
уравнению тренда с использованием МНК.
, полученных при выравнивании динамического ряда по
уравнению тренда с использованием МНК.
С помощью аналитического
выравнивания по прямой получаем  ,
, 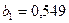 и, соответственно,
уравнение тренда
и, соответственно,
уравнение тренда  . Коэффициент сглаживания
. Коэффициент сглаживания  выбирается после
содержательного анализа исследуемого процесса в зависимости от относительной
ценности прошлых данных. Если необходимо придать больший вес последним данным,
что значение выбирается близким к единице, если необходимо учесть большую часть
имеющихся данных, то берутся небольшие значения коэффициента сглаживания. В
качестве метода выбора оптимального значения
выбирается после
содержательного анализа исследуемого процесса в зависимости от относительной
ценности прошлых данных. Если необходимо придать больший вес последним данным,
что значение выбирается близким к единице, если необходимо учесть большую часть
имеющихся данных, то берутся небольшие значения коэффициента сглаживания. В
качестве метода выбора оптимального значения  может быть использован
следующий: динамический ряд делится на две части; по первой части ряда для
различных значений
может быть использован
следующий: динамический ряд делится на две части; по первой части ряда для
различных значений  строится модель и
осуществляется прогнозирование на период, соответствующий длине второй части. Оптимальное
значение выбирается
строится модель и
осуществляется прогнозирование на период, соответствующий длине второй части. Оптимальное
значение выбирается  по минимальной
среднеквадратической ошибке уравнения.
по минимальной
среднеквадратической ошибке уравнения.
Для дальнейших расчетов
используем  . Система уравнений для определений
. Система уравнений для определений 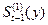 и
и 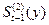 будет иметь следующий
вид:
будет иметь следующий
вид:

Из системы уравнений получаем  и
и 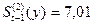 .
.
Для получения текущих значений
скользящих средних используется формула, выведенная Р.Брауном. Для линейной
модели скользящих средних определяются следующим образом:
 ;
;
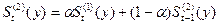 .
.
Например, для февраля  и
и 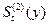 и рассчитываются
следующим образом:
и рассчитываются
следующим образом:
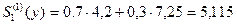
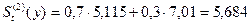 .
.
Таблица
7
|
Месяц
|
Выпуск продукции тыс. т
|

|

|
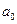
|
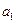
|
Выровнен-ные значения выпуска
продукции, тыс. т
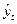
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
Январь
|
4,2
|
|
|
|
|
|
|
Февраль
|
5,3
|
5,115
|
5,684
|
4,546
|
-1,326
|
3,220
|
|
Март
|
6,3
|
5,245
|
5,337
|
5,113
|
-0,308
|
4,805
|
|
Апрель
|
6,4
|
5,984
|
5,802
|
6,166
|
0424
|
6,590
|
|
Май
|
5,7
|
6,275
|
6,133
|
6,417
|
0,331
|
6,748
|
|
Июнь
|
6,5
|
5,873
|
5,951
|
5,795
|
-0,182
|
5,613
|
|
Июль
|
6,4
|
6,312
|
6,204
|
6,420
|
0,252
|
6,168
|
|
Август
|
7,6
|
6,374
|
6,323
|
6,425
|
0,119
|
6,544
|
|
Сентябрь
|
8,4
|
7,232
|
6,959
|
7,505
|
0,636
|
8,141
|
|
Октябрь
|
10,1
|
8,050
|
7,723
|
8,377
|
0,762
|
9,139
|
|
Ноябрь
|
11,2
|
9,485
|
8,956
|
10,014
|
1,233
|
11,247
|
|
Декабрь
|
11,8
|
10,686
|
10,167
|
11,205
|
1,209
|
12,414
|
Результаты расчетов скользящих
средних представлены в гр. 3 и 4 табл.7. Параметры 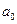 и
и 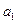 ,. исходя из (1), определяются с использованием уже рассчитанных
в гр.3 и 4 табл.7 значений
,. исходя из (1), определяются с использованием уже рассчитанных
в гр.3 и 4 табл.7 значений  и
и 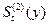 . Параметры
. Параметры 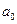 и
и 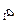 (см.гр.5 и 6 табл.7) используются в качестве коэффициентов
прямой для расчета выровненных уровней. Например, для февраля 4,546; 1,326 ;
3,220 и т.д. (см. гр.7 табл.7).
(см.гр.5 и 6 табл.7) используются в качестве коэффициентов
прямой для расчета выровненных уровней. Например, для февраля 4,546; 1,326 ;
3,220 и т.д. (см. гр.7 табл.7).
Таким образом, мы видим, что
одним из существенных преимуществ методов, основанных на экспоненциальном
сглаживании, является возможность учета временной ценности информации и
адаптации к изменяющимся условиям, что имеет большое практическое значение при
нестабильном протекании экономических процессов.
Другим преимуществом
экспоненциального сглаживания является то, что в отличие от метода скользящей
средней при использовании экспоненциального сглаживания существует возможность
построения прогнозных оценок уровней динамического ряда. Используя оценки
параметров на момент времени, могут быть получены прогнозы уровней ряда.
Рассчитаем для 2002 г.
Скользящие средние рассчитываются следующим образом:
 ,
,
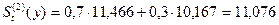 .
.
Соответственно, значения
параметров тренда 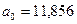 и
и 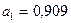 . Подставляя значения параметров в уравнение прямой, получим
прогнозное значение выпуска продукции
. Подставляя значения параметров в уравнение прямой, получим
прогнозное значение выпуска продукции  .
.
Экспоненциальное сглаживание
как метод выравнивания лежит в основе более сложных методов адаптивного моделирования.
Например, Уинтерсом была предложена модель, учитывающая сезонную составляющую
динамического ряда. Эти методы могут быть использованы для оценки тенденций
развития различных общественных явлений.
2. Технология выявления тенденции методом аналитического
выравнивания по прямой
Рассмотрим
аналитическое выравнивание по прямой ряда динамики строительства жилья концерном
«Сибирь» (см. данные табл.1). Расчет параметров уравнения прямой представлен в
табл.8.
Таблица 8
|
Годы
|
Построено жилищно-строитель-ными
коопера-тивами, млн. кв.м
yi
|
Услов-ные обозна-чения
периодов,
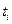
|

|
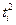
|
Выравнен-ные уровни ряда
динамики, млн. кв.м
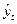
|

|
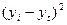
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
1999
2000
2001
2002
2003
|
2,9
2,4
2,1
1,9
1,8
|
-2
-1
0
+1
+2
|
-5,8
-2,4
0
1,9
3,6
|
4
1
0
1
4
|
2,76
2,49
2,22
1,95
1,68
|
0,14
-0,09
-0,12
-0,05
0,12
|
0,0196
0,0081
0,0144
0,0025
0,0144
|
|
итого
|
11,1
|
|
-2,7
|
10
|
11,10
|
0,00
|
1,0590
|
Используя
итоги граф 2, 4 и 5, определим параметры уравнения прямой:
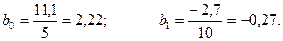
По рассчитанным параметрам записываем уравнение
прямой ряда динамики, характеризующего строительство жилья
жилищно-строительными кооперативами:
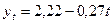 .
.
Используя приведенное уравнение, рассчитаем для
каждого года теоретические значения:
для
1999 г. 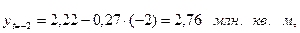
для
2000 г.  (см. итоги гр.2 и 6 табл.8).
(см. итоги гр.2 и 6 табл.8).
Правильность
расчета уровней выравниваемого ряда динамики может быть проверена следующим
образом: сумма значений эмпирического ряда должна совпадать с суммой
вычисленных уровней выровненного ряда, т.е. 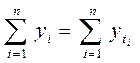 (см. итоги гр. 2 и 6).
(см. итоги гр. 2 и 6).
Продление
в будущее тенденции, наблюдавшейся в прошлом, носит название экстраполяции. Экстраполируя при 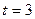 , находим уровень 2002 г., равный
, находим уровень 2002 г., равный 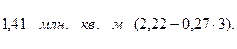
Возможность
экстраполяции обеспечивается двумя обстоятельствами:
1)
общие условия, определяющие тенденцию развития в прошлом, не претерпевают
существенных изменений в будущем;
2)
тенденция развития явления характеризуется тем или иным аналитическим
уравнением.
Общая
тенденция развития может быть охарактеризована с помощью содержательного
экономического анализа. Вместе с тем расчет таких показателей, как скорость
роста, темпы роста, пункты роста, позволяет ориентироваться в наличии или
отсутствии устойчивой тенденции развития и обосновать форму уравнения тренда.
Если условия формирования уровней ряда изменяются, то расчет параметров
уравнения не следует вести по данным за весь рассматриваемый период времени. В
этом случае целесообразно разбить ряд динамики на ряд этапов, ориентируясь на
устойчивость абсолютных приростов или пунктов роста. Значение 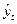 , полученное в результате экстраполяции, используют для
определения прогнозного значения на будущее.
, полученное в результате экстраполяции, используют для
определения прогнозного значения на будущее.
При
составлении прогнозов оперируют не точечной, а интервальной оценкой, определяя
так называемые доверительные интервалы
прогноза. Величина доверительного интервала определяется в общем виде так:
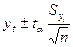 ,
,
где 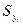 - среднее квадратическое отклонение от тренда;
- среднее квадратическое отклонение от тренда;
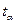 - табличное значение t-критерия Стьюдента при уровне значимости
- табличное значение t-критерия Стьюдента при уровне значимости  .
.
Величина 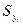 определяется по формуле:
определяется по формуле:
 ,
,
где
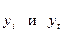 - соответственно
фактические и расчетные значения уровней
- соответственно
фактические и расчетные значения уровней
динамического ряда;
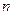 - число уровней ряда;
- число уровней ряда;
 - количество
параметров в уравнении тренда (для уравнения прямой
- количество
параметров в уравнении тренда (для уравнения прямой
 ).
).
Используя данные гр.8 табл.8, рассчитаем среднюю
квадратическую ошибку линейного уравнения тренда;
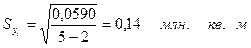
Отсюда величина относительной ошибки составляет 6,32%:
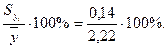
Величина средней квадратической ошибки может быть
рассчитана иным способом, позволяющим избежать ошибки при округлениях величины  . Для уравнения линейного тренда
. Для уравнения линейного тренда 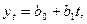 величина
величина 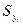 определяется по
формуле:
определяется по
формуле:

Для примера, приведенного в
табл.5, получим, получим 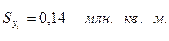

Если воспользоваться методом
конечных разностей для выбора формы уравнения тренда, то из данных гр.4 табл.1
можно видеть, что абсолютные приросты не являются постоянными, а начиная с 2001
г. постоянными будут вторые разности (разности абсолютных приростов). В этом
случае, как было показано выше, для выравнивания может использоваться парабола
второго порядка:
 .
.
Система нормальных уравнений
для нахождения параметров уравнения параболы (при соблюдении принципа отсчета
от условного начала) будет иметь вид:
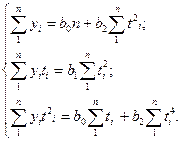
Расчет параметров этого
уравнения представлен в табл.6.
Подставляем итоги гр.2, 4, 5,
6 и 7 табл.6 и получаем следующую систему уравнений для данного временного
ряда:

Таблица
9
|
Годы
|
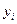
|
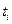
|
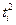
|

|
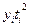
|

|
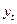
|

|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
1999
|
2,9
|
-2
|
4
|
-5,8
|
11,6
|
16
|
2,889
|
+0,011
|
|
2000
|
2,4
|
-1
|
1
|
-2,4
|
2,4
|
1
|
2,426
|
-0,026
|
|
2001
|
2,1
|
0
|
0
|
0
|
0
|
0
|
2,091
|
+0,009
|
|
2002
|
1,9
|
+1
|
1
|
1,9
|
1,9
|
1
|
1,886
|
+0,014
|
|
2003
|
1,8
|
+2
|
4
|
3,6
|
7,2
|
16
|
1,809
|
-0,009
|
|
Итого
|
11,1
|
0
|
10
|
-2,7
|
23,1
|
34
|
11,10
|
0,00
|
Решая систему уравнений,
определим значения параметров уравнения параболы второго порядка:

Отсюда уравнение параболы
второго порядка, характеризующего тенденцию строительства жилья
жилищно-строительными кооперативами, будет записано так:
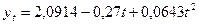 .
.
Величина среднего
квадратического отклонения фактических уровней динамического ряда от выровненных
для уравнения параболы второго порядка определится по формуле:
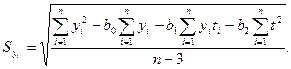
т.е.
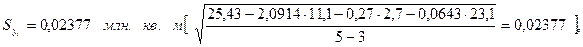
относительная ошибка уравнения составить 1,07%. Сравнив
полученные значения 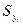 для уравнения прямой и
параболы второго порядка, можно сделать вывод о том, что парабола более точно
описывает основную тенденцию ряда динамики, характеризующего строительство
жилья жилищно-строительными кооперативами.
для уравнения прямой и
параболы второго порядка, можно сделать вывод о том, что парабола более точно
описывает основную тенденцию ряда динамики, характеризующего строительство
жилья жилищно-строительными кооперативами.
Прогноз на 2005 г. по
уравнению параболы второго порядка будет составлен следующим образом:
1)
экстраполируя для 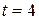 , получаем
, получаем 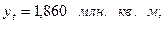
2)
значение критерия Стьюдента при уровне значимости 5% и
числе степеней свободы 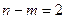 равно 4,303.
равно 4,303.
Таким образом, с вероятностью
95% можно ожидать, что в 2005 г. строительный концерн «Сибирь» построить жилья
не меньше, чем 1,814 млн. кв. м., но не больше 1,906 млн. кв. м.
Приведенные расчеты следует
рассматривать не как завершающую стадию прогнозирования, а лишь как
предварительный этап в разработке прогноза. Для составления прогноза должна
быть привлечена дополнительная информация, не содержащаяся в самом динамическом
ряду.
ЗАКЛЮЧЕНИЕ
Любая экономическая деятельность основывается на
анализе показателей и данных,
характеризующих результаты этой деятельности. В основе этого анализа лежит
статистическая наука, предоставляющая инструментарий для анализа.
Одной
из важнейших задач статистики является изучение изменений анализируемых
показателей во времени. Эти изменения можно изучать, если иметь данные по
определенному кругу показателей на ряд моментов времени или за ряд промежутков
времени, следующих друг за другом. Таким образом временные ряды (динамические)
являются важным инструментом статистического анализа, что обусловливает
актуальность выбранной темы.
В
данной курсовой работе была поставлена и выполнена цель - охарактеризовать
методы выявления тенденции в рядах динамики, что является одной из главнейших
задач, возникающих при анализе рядов динамики. В процессе работы были даны
характеристики следующим основных методам выявления тенденции в рядах динамики:
метода укрупнения интервала
динамического ряда, метода скользящей средней, метода аналитического выравнивания,
метода конечных разностей, методов адаптивного моделирования и прогнозирования.
В
работе были поставлены и решены
следующие задачи: характеристика основных методов выявления тенденции в рядах
динамики; сравнение методов выявления
тенденции в рядах динамики; ранжирование методов по степени их сложности и
применимости в анализе временных рядов.
В
курсовой работе рассмотрена технология выявления тенденции аналитического
выравнивания по прямой на конкретном примере показателей коммерческой
деятельности строительного концерна «Сибирь».
СПИСОК
ЛИТЕРАТУРЫ
1.
Ефимова М.Р., Петрова Е.В., Румянцева В.Н. Общая теория
статистики: Учебник. – М., 2002. – 416 с.
2.
Елисеева И.И., Юзбашев М.М. Общая теория статистики. –
М., 1995. - 456 с.
3.
Ефимова М.Р., Рябцев В.М. Общая теория статистики. –
М., 1991. – 389 с.
4.
Кендэл М. Временные ряды / Пер. с англ. Ю.П.Лукашина. –
М., 1981. – 290 с.
5.
Льюис К.Д. Методы прогнозирования экономических
показателей / Пер. с англ. Е.З.
Демиденко. – М., 1986. – 370 с.
6.
Миллс Ф. Статистические методы. / пер. с англ. – М.,
1990. – 456 с.
7.
Рябушкин Т.В., Ефимова М.Р., Ипатова И.М. и др. Общая
теория статистики. – М.: 1990. – 567 с.
8.
Статистический анализ в экономике / Под ред.
Г.Л.Громыко. – М., 1992. – 450 с.
9.
Статистический словарь. / под ред. М.А.Королева. – М., 1989. – 560 с.
10. Статистическое
моделирование и прогнозирование: Учебное пособие. / Под ред. А.Г.Гранберга. –
М., 1990. – 289 с.
11. Четыркин
Е.М. Статистические методы прогнозирования. – М., 1975. – 349 с.
12. www. Sibir-stroy.ru