Задача 1
Оборот и среднесписочная численность работников 20 торговых предприятий за отчетный период следующие:
|
№ п/п |
Оборот, тыс.руб. |
Среднесписочная численность работников, чел. |
|
1 |
131,3 |
5 |
|
2 |
31,1 |
2 |
|
3 |
164,4 |
4 |
|
4 |
32,7 |
2 |
|
5 |
161,5 |
6 |
|
6 |
67,9 |
5 |
|
7 |
64,9 |
3 |
|
8 |
102,3 |
5 |
|
9 |
89,2 |
4 |
|
10 |
165,4 |
5 |
|
11 |
140,2 |
6 |
|
12 |
114,6 |
4 |
|
13 |
57,8 |
3 |
|
14 |
73,4 |
5 |
|
15 |
87,5 |
4 |
|
16 |
50,8 |
2 |
|
17 |
111,0 |
4 |
|
18 |
93,5 |
3 |
|
19 |
171,1 |
6 |
|
20 |
48,4 |
2 |
С целью выявления зависимости между объемом оборота и средней выработки на одного работника произвести группировку предприятий по размеру оборота, образовав четыре группы с равными интервалами. В каждой группе и по итогу в целом посчитать:
1) количество предприятий;
2) объем оборота – всего, и в среднем на одно предприятие;
3) среднесписочное число работников – всего и в среднем на одно предприятие;
4) среднюю выработку (оборот на одного работника);
Результаты группировки оформить в разработочной и групповой таблицах.
Сделать выводы.
Решение
Минимальное значение: 31,1
Максимальное значение: 171,1
Размах: 171,1 – 31,1 = 140
Размах одной группы 140 / 4 = 35
1) Построим рабочую таблицу:
|
Группа |
Предприятие |
Оборот, тыс. руб. |
Среднесписочная численность работников, чел. |
|
31,1 – 66,1 |
2 |
31,1 |
2 |
|
4 |
32,7 |
2 |
|
|
7 |
64,9 |
3 |
|
|
13 |
57,8 |
3 |
|
|
16 |
50,8 |
2 |
|
|
20 |
48,4 |
2 |
|
|
Итого 1-ая группа |
6 предприятий |
285,7 |
14 |
|
Среднее по 1-ой группе |
|
47,6166667 |
2,333333333 |
|
66,1 – 101,1 |
6 |
67,9 |
5 |
|
9 |
89,2 |
4 |
|
|
14 |
73,4 |
5 |
|
|
15 |
87,5 |
4 |
|
|
18 |
93,5 |
3 |
|
|
Итого 2-ая группа |
5 предприятий |
411,5 |
21 |
|
Среднее по 2-ой группе |
|
82,3 |
4,2 |
|
101,1 – 136,1 |
1 |
131,3 |
5 |
|
8 |
102,3 |
5 |
|
|
12 |
114,6 |
4 |
|
|
17 |
111 |
4 |
|
|
Итого 3-ая группа |
4 предприятия |
459,2 |
18 |
|
Среднее по 3-ей группе |
|
114,8 |
4,5 |
|
136,1 – 171,1 |
3 |
164,4 |
4 |
|
5 |
161,5 |
6 |
|
|
10 |
165,4 |
5 |
|
|
11 |
140,2 |
6 |
|
|
19 |
171,1 |
6 |
|
|
Итого 4-ая группа |
5 предприятий |
802,6 |
27 |
|
Среднее по 4-ой группе |
|
160,52 |
5,4 |
|
Всего |
|
1959 |
80 |
По каждой группе и в целом по совокупности подсчитаем:
1. Количество предприятий
Группа 31,1 – 66,1: 6
Группа 66,1 – 101,1: 5
Группа 101,1 – 136,1: 4
Группа 136,1 – 171,1: 5
В целом 20 предприятий
2. Объем оборота – всего и в среднем на одно предприятие
Всего: 131,3 + 31,1 + 164,4 + 32,7 + 161,5 + 67,9 + 64,9 + 102,3 + 89,2 +
+ 165,4 + 140,2 + 114,6 + 57,8 +73,4 + 87,5 + 50,8 + 111,0 + 93,5 +
+ 171,1 + 48,4 = 1959
В среднем не одно предприятие: 1959 / 20 = 97,95
3. Среднесписочное число работников
Всего: 5 + 2 + 4 + 2 + 6 + 5 + 3 + 5 + 4 + 5 + 6 + 4 + 3 + 5 + 4 + 2 + 4 + 3 +
+ 6 + 2 = 80
В среднем на одно предприятие: 80 / 40 = 4
4. Средняя выработка (оборот на одного работника):
1959 / 80 = 24,4875
2) Построим сводную таблицу:
|
Группа |
Кол-во предприятий |
Оборот |
Среднесписочная численность |
Оборот 1 рабочего |
||
|
Всего |
На 1 пред-е |
Всего |
На 1 пред-е |
|||
|
1 |
6 |
285,7 |
47,61666667 |
14 |
2,33333333 |
20,4071429 |
|
2 |
5 |
411,5 |
82,3 |
21 |
4,2 |
19,5952381 |
|
3 |
4 |
459,2 |
114,8 |
18 |
4,5 |
25,5111111 |
|
4 |
5 |
802,6 |
160,52 |
27 |
5,4 |
29,7259259 |
|
ИТОГО: |
1959 |
|
80 |
|
|
Выводы: Наибольшее число предприятий (6) попадает в первую группу с интервалом 31,1 – 66,1, а наименьшее (4) попадает в третью группу с интервалом 101,1 – 136,1.
Задача 13
Производство однородной продукции предприятиями объединения составила:
|
Предприятие |
Фактически произведено продукции млн.руб. |
Выполнение плана, % |
Удельный вес продукции первого сорта, % |
|
1-е |
41,2 |
103 |
85 |
|
2-е |
20,9 |
95 |
80 |
|
3-е |
32,1 |
107 |
90 |
Вычислить:
1) процент выполнения плана выпуска продукции в среднем по объединению;
2) средний процент выпуска продукции первого сорта по объединению.
Дать обоснование применения формул средних для расчета показателей. Сделать выводы.
Решение
1) Процент выполнения плана в среднем по объединению:
(41,2*103 + 20,9*95 + 32,1*107) / (41,2 + 20,9 + 32,1) = 102,5881
2) Средний процент выпуска продукции первого сорта по объединению
(41,2*85 + 20,9*80 + 32,1*90) / (41,2 + 20,9 + 32,1) = 85,595
Выводы. Второе предприятие выполнило план ниже среднего показателя по объединению, а первое и третье предприятия выполнили план выше среднего уровня.
Средний процент продукции первого сорта по всем предприятия составил 85,6%. Первое и второе предприятия выполнили продукции первого сорта меньше среднего, а третье предприятие – выше среднего.
Задача 30
Торговая площадь магазинов организации на начало года характеризуется следующими данными:
|
Год |
Торговая площадь, кв.м. |
|
1 |
687 |
|
2 |
707 |
|
3 |
722 |
|
4 |
758 |
|
5 |
808 |
Определить:
1) вид динамического ряда;
2) средний уровень динамического ряда;
3) абсолютные приросты, темпы роста и прироста цепные и базисные, абсолютное содержание 1% прироста;
4) средний абсолютный прирост, средний темп роста и прироста уровней динамического ряда.
Результаты расчетов представить в таблице. Изобразить динамический ряд на графике. Сделать выводы.
Решение
1. Вид динамического ряда: интервальный, абсолютный, так как заданы абсолютные значения параметров.
2. Средний уровень ряда
(707 + 722 + 758 + 808) / 4 = 748,75
3. Рассчитаем абсолютные приросты, темпы роста и прироста (цепные и базисные), абсолютное содержание 1% прироста:
|
Год |
Торговая площадь |
Абсолютный прирост |
Темп роста |
Темп прироста |
Значение 1% прироста |
|||
|
Цепной |
Базисный |
Цепной |
Базисный |
Цепной |
Базисный |
|||
|
1 |
687 |
Х |
Х |
Х |
Х |
Х |
Х |
Х |
|
2 |
707 |
20 |
20 |
1,03 |
1,03 |
0,03 |
0,03 |
6,87 |
|
3 |
722 |
15 |
35 |
1,02 |
1,05 |
0,02 |
0,05 |
7,07 |
|
4 |
758 |
36 |
71 |
1,05 |
1,10 |
0,05 |
0,10 |
7,22 |
|
5 |
808 |
50 |
121 |
1,07 |
1,18 |
0,07 |
0,18 |
7,58 |
|
Итого |
3682 |
121 |
247 |
Х |
Х |
Х |
Х |
Х |
Приведенные показатели рассчитываются следующим образом:
Абсолютный цепной прирост за год N, где N>1 равен разности:
(Торговая площадь за N год) – (Торговая площадь за N-1 год)
Абсолютный базисный прирост за год N, где N>1 равен разности:
(Торговая площадь за N год) – (Торговая площадь за 1 год)
Цепной темп роста за год N, где N>1 вычисляется:
(Торговая площадь за N год) / (Торговая площадь за N-1 год)
Базисный темп роста за год N, где N>1 вычисляется:
(Торговая площадь за N год) / (Торговая площадь за 1 год)
Цепной темп прироста за год N, где N>1 вычисляется:
(Цепной темп роста за N год) - 1
Базисный темп прироста за год N, где N>1 вычисляется:
(Цепной темп прироста за N год) - 1
Значений 1% прироста за год N, где N>1 вычисляется как:
(Торговая площадь за N год) / 100
4. Средний абсолютный прирост, средний темп роста и прироста уровней динамического ряда
Средний абсолютный прирост: 121 / 4 = 30,25
Средний темп роста: (1,03 + 1,05 + 1,1 + 1,18) / 4 = 1,09
Средний темп прироста: (0,03 + 0,05 + 0,1 + 0,18) / 4 = 0,09
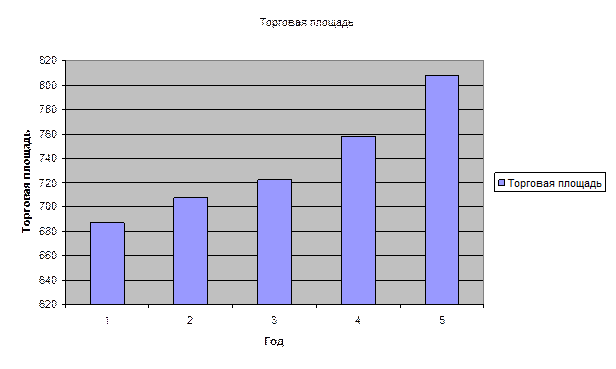
На приведенной выше гистограмме показано изменение размеров торговых площадей за 5 лет.
Задача 54
Продажи товара А на рынках города за два периода составили:
|
Рынок |
Базисный период |
Отчетный период |
||
|
цена за 1 кг, руб |
продано, кг |
цена за 1 кг, руб |
продано, кг |
|
|
|
p0 |
q0 |
p1 |
q1 |
|
1-й |
18 |
180 |
20 |
170 |
|
2-й |
16 |
230 |
19 |
250 |
Определить:
1) индекс средней цены (индекс цен переменного состава);
2) индекс цен в неизменной структуре продажи (индекс цен постоянного состава);
3) индекс структурных сдвигов в объеме продажи.
Показать взаимосвязь индексов. Сделать выводы.
Решение.
Для расчета индексов необходимо определить общую стоимость
товаров (товарооборот) за базисный период (![]() ), отчетный период (
), отчетный период (![]() ) и условную стоимость отчетного периода по ценам базисного
) и условную стоимость отчетного периода по ценам базисного ![]() , представленные в таблице.
, представленные в таблице.
1. Индекс средней цены (переменного состава)
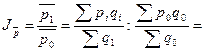
![]()
2. Индекс цен постоянного состава
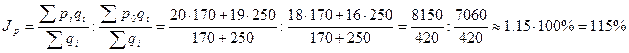
3. Индекс структурных сдвигов
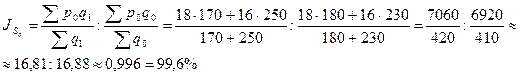
Выводы. Средняя цена единицы товара в отчетном периоде по сравнению с базисным возросла на 15% (115-100), за счет изменения цен постоянного состава.
Задача 67
Данные о движении кадров производственного предприятия за два года:
|
Показатели |
Базисный год |
Отчетный год |
|
Численность работников на начало года |
315 |
308 |
|
Принято работников |
25 |
21 |
|
Уволено работников |
32 |
29 |
|
В том числе: |
|
|
|
по собственному желанию |
5 |
2 |
|
по сокращению штатов |
12 |
16 |
|
на пенсию, по инвалидности, по призыву в армию |
10 |
8 |
|
за нарушение трудовой дисциплины, ввиду несоответствия занимаемой должности |
5 |
3 |
Определить численность работников на конец каждого года, абсолютные и относительные показатели движения кадров за каждый год.
Дать оценку изменения интенсивности движения работников.
Сделать выводы.
Решение
Численность работников на конец базисного года: 308 человек
Численность работников на конец отчетного периода:
308 + 21 – 29 = 300
Показатели движения кадров сведены в таблице:
|
Абсолютные показатели |
Базисный год |
Отчетный год |
|
Общий оборот |
57 |
50 |
|
Текучесть кадров |
10 |
5 |
|
Относительные показатели |
Базисный год |
Отчетный год |
|
Среднесписочная численность |
312 |
304 |
|
Коэффициент по приему |
0,08 |
0,069 |
|
Коэффициент по увольнению |
0,103 |
0,095 |
|
Коэффициент текучести |
0,032 |
0,016 |
Значительно увеличился коэффициент по приему кадров с 0,08 до 0,069 уменьшился коэффициент увольнения, и коэффициент текучести кадров также снизился с 0,032 до 0,016.
Все это снижает падение численности персонала предприятия и является безусловно позитивным фактом.
Задача 70
Данные статистической отчетности предприятия за два периода:
|
Показатели |
Базисный период |
Отчетный период |
|
Оборот, тыс. руб. |
3433 |
5684 |
|
Средняя списочная численность работников, чел. |
36 |
38 |
|
Фонд заработной платы, тыс. руб. |
427,2 |
567,0 |
Определить:
1) среднюю заработную плату и среднюю выработку одного работника за каждый период;
2) абсолютный прирост фондов заработной платы – всего, в том числе за счет изменения численности работников и средней заработной платы;
3) долю влияния изменения численности работников и средней заработной платы на общий прирост фонда заработной платы;
4) абсолютный прирост оборота – всего, в том числе за счет изменения численности работников и средней выработки.
Сделать выводы.
Решение
1. Средняя зарплата и средняя выработка одного работника за каждый период:
средняя
зарплата за базисный период ![]()
средняя
зарплата за отчетный период ![]()
средняя
выработка за базисный период ![]()
средняя
выработка за отчетный период ![]()
2. Абсолютный прирост фонды заработной платы:
всего ![]() = 567000 – 427200 = 139800
= 567000 – 427200 = 139800
3. долю влияния изменения численности работников и средней заработной платы на общий прирост фонда заработной платы
|
Показатели |
Базисный период |
Отчетный период |
Индексы |
|
Оборот, тыс. руб. |
3433 |
5684 |
1,656 |
|
Средняя списочная численность работников, чел. |
36 |
38 |
1,055 |
|
Фонд заработной платы, тыс. руб. |
427,2 |
567,0 |
1,327 |
За счет изменения численности: ![]() 38 – (38 / 1,055) = 1,981
38 – (38 / 1,055) = 1,981
За счет изменения средней зарплаты: 567000 – (567000 / 1,327) = 139720,422
ВЫВОДЫ: общий прирост фонда заработной платы возрастает большей частью за счет изменения средней заработной платы.
Задача 103
Товарные запасы потребительского общества составили на 1-е число каждого месяца в тыс. руб.: 1.01 – 24; 1.02 – 26; 1.03 – 28; 1.04 – 30; 1.05 – 25; 1.06 – 26; 1.07 – 32. Оборот I квартала – 63 тыс. руб., II квартала – 72 тыс.руб.
Вычислить за каждый квартал:
1) средние товарные запасы;
2) товарные запасы в процентах к обороту;
3) оборачиваемость товарных запасов в днях и в числе оборотов.
Сделать выводы.
Решение.
1. Средние товарные запасы:
(24000 + 26000 + 28000 + 30000 + 25000 + 26000 + 32000) / (31 + 28 + 31 + 30 + 31 + 30 + 31) = 900
2. Товарные запасы в процентах к обороту:
за первый
квартал: ![]()
за второй
квартал: ![]()
3. Оборачиваемость товарных запасов:
средний оборот
за день: ![]()
оборачиваемость
в днях: 1 квартал ![]()
![]()
2
квартал ![]()
оборачиваемость в числе оборотов:
1
квартал ![]()
2
квартал ![]()
Выводы. Товарные запасы превосходят товарооборот в первом квартале на 43%, а во втором квартале на 25%. Оборачиваемость товарных запасов в 1-ом квартале составляет 84,5 дней или 1,0655 оборота; во 2-ом квартале – 96,5.
За первый квартал совершено 1,0655 оборота, а за второй 0,953.
Задача 115
Оборот предприятия увеличился на 18%, а сумма издержек обращения возросла на 12%.
Определить, как изменился уровень издержек обращения. Привести формулы используемых индексов. Показать их взаимосвязь.
Решение
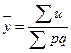
![]()
![]()
![]()
Выводы. Уровень издержек изменился в 0,95 раза.