Вариант 1
1.
Найти среднее арифметическое, медиану, моду, среднее геометрическое, размах,
среднее квадратическое отклонениедисперсию, коэффициент вариации.
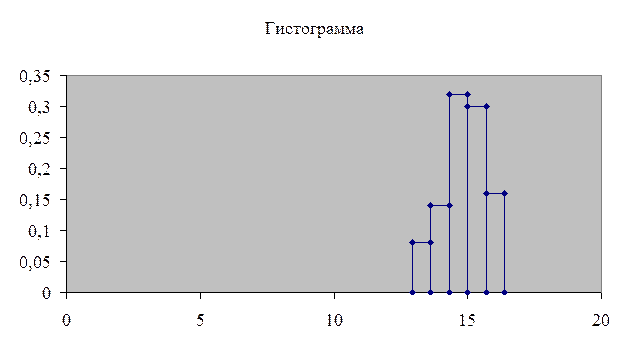
2. Построить гистограмму,
предварительно разбив выборку на 5 интервалов.
3. Осуществить проверку гипотезы
о среднем значении нормально распределенной генеральной совокупности при
известной дисперсии.
4. Осуществить проверку гипотезы о
среднем значении нормально распределенной генеральной совокупности при
неизвестной дисперсии.
5. Осуществить проверку гипотезы
о дисперсии нормально распределенной генеральной совокупности.
6. Осуществить проверку гипотезы о
согласии с нормальным распределением с параметром сдвига 15, параметром
масштаба 0,8 с использованием критерия 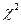 Пирсона.
Пирсона.
7. По выборке из первых 10 наблюдений
осуществить проверку гипотезы о согласии с нормальным распределением с
параметром сдвига 15, параметром масштаба 0,8 с использованием
непараметрических критериев Колмогорова, Смирнова, 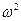 ,
, 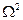 , Мизеса.
, Мизеса.
|
14,70
|
14,31
|
14,40
|
14,81
|
13,33
|
14,36
|
14,94
|
16,18
|
15,18
|
15,19
|
|
14,07
|
14,83
|
16,09
|
14,31
|
16,32
|
15,39
|
15,09
|
13,98
|
15,59
|
15,18
|
|
14,16
|
15,31
|
13,53
|
15,74
|
16,38
|
15,75
|
15,27
|
13,58
|
14,87
|
15,25
|
|
14,53
|
15,32
|
14.60
|
15,14
|
12,93
|
15,73
|
14,04
|
13,95
|
15,69
|
14,48
|
|
15,01
|
14,88
|
14,54
|
13,92
|
15,30
|
14,58
|
14,67
|
15,69
|
15,01
|
14,87
|
Решение.
1.
Чтобы найти среднее
арифметическое, медиану, моду, размах, среднее квадратическое отклонение,
дисперсию, коэффициент вариации используем описательную статистику в редакторе
ЕXCEL:
|
Описательная статистика
|
|
Среднее
|
14,8594
|
|
Стандартная ошибка
|
0,108827
|
|
Медиана
|
14,875
|
|
Мода
|
15,01
|
|
Стандартное отклонение
|
0,769525
|
|
Дисперсия выборки
|
0,592169
|
|
Эксцесс
|
-0,0887
|
|
Асимметричность
|
-0,20968
|
|
Интервал
|
3,45
|
|
Минимум
|
12,93
|
|
Максимум
|
16,38
|
|
Сумма
|
742,97
|
|
Счет
|
50
|
Получаем:
среднее арифметическое - 14,8594,
медиана - 14,875,
мода - 15,01,
размах - 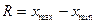 = 3,45,
= 3,45,
среднее квадратическое отклонение - 0,769525,
дисперсия - 0,592169.
Коэффициент вариации 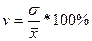 = 0,769525 / 14,8594 * 100 = 5,179%.
= 0,769525 / 14,8594 * 100 = 5,179%.
Среднее геометрическое 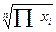 = 14,84.
= 14,84.
2.
Разбиваем выборку на 5 интервалов.
При
n=5 получаем
размер интервала 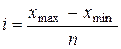 = 3,45/5= 0,69.
= 3,45/5= 0,69.
Находим границы интервалов и считаем количество
точек в каждом интервале:
|
№ интервала
|
Левая граница
|
Правая граница
|
Количество точек интервала
|
Частота
|
|
1-й интервал
|
12,93
|
13,62
|
4
|
0,08
|
|
2-й интервал
|
13,62
|
14,31
|
7
|
0,14
|
|
3-й интервал
|
14,31
|
15
|
16
|
0,32
|
|
4-й интервал
|
15
|
15,69
|
15
|
0,3
|
|
5-й интервал
|
15,69
|
16,38
|
8
|
0,16
|
3. Осуществим проверку гипотезы о
среднем значении 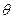 нормально
распределенной генеральной совокупности при известной дисперсии.
нормально
распределенной генеральной совокупности при известной дисперсии.
Гипотеза: 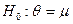 . Для
проверки такой гипотезы воспользуемся
критерием, статистика которого имеет вид:
. Для
проверки такой гипотезы воспользуемся
критерием, статистика которого имеет вид: 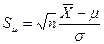 .
.
Пусть 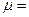 15, известная дисперсия
15, известная дисперсия 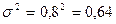 . Тогда
. Тогда  .
.
Критическое
значение статистики 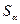 при уровне значимости
при уровне значимости 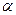 = 0.05 равно 1.645. Так как вычисленное по выборке
значение статистики не превышает критического, то проверяемая гипотеза о
согласии не отвергается.
= 0.05 равно 1.645. Так как вычисленное по выборке
значение статистики не превышает критического, то проверяемая гипотеза о
согласии не отвергается.
4.
Осуществим проверку гипотезы о среднем значении 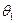 нормально
распределенной генеральной совокупности при неизвестной дисперсии.
нормально
распределенной генеральной совокупности при неизвестной дисперсии.
Гипотеза: 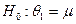 . Для
проверки такой гипотезы воспользуемся
критерием, статистика которого имеет вид:
. Для
проверки такой гипотезы воспользуемся
критерием, статистика которого имеет вид: 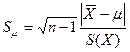 .
.
Пусть 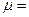 15. Тогда
15. Тогда 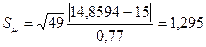 .
.
Критическое
значение статистики 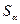 при уровне значимости
при уровне значимости 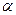 = 0.05 равно 1.67. Так как вычисленное по выборке
значение статистики не превышает критического, то проверяемая гипотеза о
согласии не отвергается.
= 0.05 равно 1.67. Так как вычисленное по выборке
значение статистики не превышает критического, то проверяемая гипотеза о
согласии не отвергается.
5.
Осуществим проверку гипотезы о дисперсии нормально распределенной генеральной
совокупности.
Гипотеза: 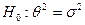 . Для
проверки такой гипотезы воспользуемся
критерием, статистика которого имеет вид:
. Для
проверки такой гипотезы воспользуемся
критерием, статистика которого имеет вид: 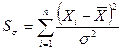 .
.
Составляем таблицу значений 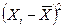 =
=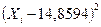
|
0,025
|
0,302
|
0,211
|
0,002
|
2,339
|
0,249
|
0,006
|
1,744
|
0,103
|
0,109
|
|
0,623
|
0,001
|
1,514
|
0,302
|
2,133
|
0,282
|
0,053
|
0,773
|
0,534
|
0,103
|
|
0,489
|
0,203
|
1,767
|
0,775
|
2,312
|
0,793
|
0,169
|
1,637
|
0,000
|
0,153
|
|
0,109
|
0,212
|
0,067
|
0,079
|
3,723
|
0,758
|
0,671
|
0,827
|
0,690
|
0,144
|
|
0,023
|
0,000
|
0,102
|
0,882
|
0,194
|
0,078
|
0,036
|
0,690
|
0,023
|
0,000
|
Тогда 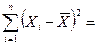 29,016.
29,016.
Пусть 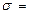 0,8. Тогда
0,8. Тогда 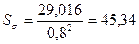 .
.
Критическое
значение статистики 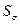 при уровне значимости
при уровне значимости 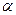 = 0.05 равно 67,5. Так как вычисленное по выборке
значение статистики не превышает критическое, то проверяемая гипотеза о
согласии не отвергается.
= 0.05 равно 67,5. Так как вычисленное по выборке
значение статистики не превышает критическое, то проверяемая гипотеза о
согласии не отвергается.
6. Осуществим проверку гипотезы о
согласии с нормальным распределением с параметром сдвига 15, параметром
масштаба 0,8 с использованием критерия 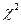 Пирсона.
Пирсона.
Гипотеза: 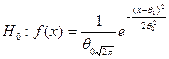 , где
, где 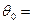 0,8,
0,8, 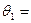 15.
15.
Для
вычисления значения статистики 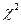 Пирсона по формуле
Пирсона по формуле
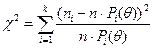
воспользуемся
результатом, полученным в п.2 при разбиении области определения
случайной величины на 5
интервалов группирования.
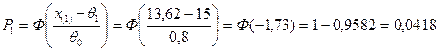
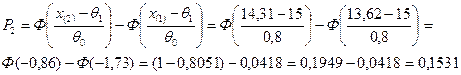
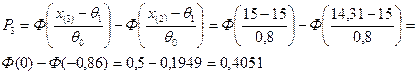
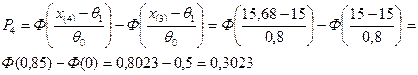
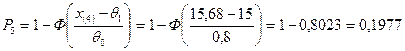 .
.
Получаем
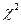 =3,056.
=3,056.
Для
уровня значимости 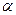 = 0.05 и
k
=5
критическое значение статистики
= 0.05 и
k
=5
критическое значение статистики  равно 9,4877.
равно 9,4877.
Сравниваем полученное значение 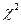 с
критическим значением статистики.. Так как вычисленное по выборке значение
статистики не превышает критического, то проверяемая гипотеза о согласии не
отвергается.
с
критическим значением статистики.. Так как вычисленное по выборке значение
статистики не превышает критического, то проверяемая гипотеза о согласии не
отвергается.
7. По выборке из первых 10 наблюдений
|
14,70
|
14,31
|
|
14,07
|
14,83
|
|
14,16
|
15,31
|
|
14,53
|
15,32
|
|
15,01
|
14,88
|
осуществим
проверку гипотезы о согласии с нормальным распределением с параметром сдвига
15, параметром масштаба 0,8 с использованием непараметрических критериев
Колмогорова, Смирнова, 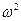 ,
, 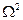 , Мизеса.
, Мизеса.
Гипотеза: 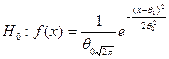 , где
, где 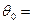 0,8,
0,8, 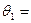 15.
15.
а)
Критерий Колмогорова
Вычисляем
значение статистики Колмогорова по формуле: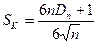 , где
, где 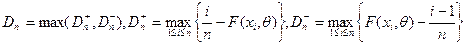 .
.
Составляем
расчетную таблицу:
|
i
|
xi
|
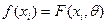
|
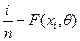
|
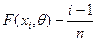
|
|
1
|
14,7
|
0,535
|
-0,435
|
0,535
|
|
2
|
14,07
|
0,980
|
-0,780
|
0,880
|
|
3
|
14,16
|
0,866
|
-0,566
|
0,666
|
|
4
|
14,53
|
0,593
|
-0,193
|
0,293
|
|
5
|
15,01
|
0,499
|
0,001
|
0,099
|
|
6
|
14,31
|
0,724
|
-0,124
|
0,224
|
|
7
|
14,83
|
0,510
|
0,190
|
-0,090
|
|
8
|
15,31
|
0,538
|
0,262
|
-0,162
|
|
9
|
15,32
|
0,540
|
0,360
|
-0,260
|
|
10
|
14,88
|
0,504
|
0,496
|
-0,396
|
|
max
|
0,496
|
0,880
|
Получаем:
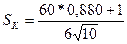 = 2,583.
= 2,583.
Для
уровня значимости 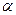 = 0.05 критическое значение статистики
= 0.05 критическое значение статистики 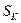 равно 1,3581.
равно 1,3581.
Так
как вычисленное по выборке значение статистики
превышает критическое, то проверяемая гипотеза о согласии отвергается.
б)
Критерий Смирнова
Вычисляем значение статистики Смирнова по формуле 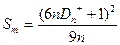
Получаем:
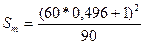 = 10,513.
= 10,513.
Для
уровня значимости 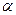 = 0.05 критическое значение статистики
= 0.05 критическое значение статистики 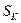 равно 5,9915.
равно 5,9915.
Так
как вычисленное по выборке значение статистики
превышает критическое, то проверяемая гипотеза о согласии отвергается.
в)
Критерий 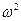 Мизеса.
Мизеса.
Вычисляем
значение статистики 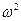 Мизеса
по формуле:
Мизеса
по формуле:

Составляем
расчетную таблицу:
|
i
|
xi
|
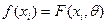
|
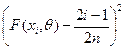
|
|
1
|
14,7
|
0,535
|
0,235
|
|
2
|
14,07
|
0,980
|
0,689
|
|
3
|
14,16
|
0,866
|
0,379
|
|
4
|
14,53
|
0,593
|
0,059
|
|
5
|
15,01
|
0,499
|
0,002
|
|
6
|
14,31
|
0,724
|
0,030
|
|
7
|
14,83
|
0,510
|
0,020
|
|
8
|
15,31
|
0,538
|
0,045
|
|
9
|
15,32
|
0,540
|
0,096
|
|
10
|
14,88
|
0,504
|
0,199
|
|
сумма
|
1,754
|
Получаем:
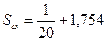 = 1,804.
= 1,804.
Для
уровня значимости 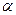 = 0.05 критическое значение статистики
= 0.05 критическое значение статистики 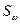 равно 0,4615.
равно 0,4615.
Так
как вычисленное по выборке значение статистики
превышает критическое, то проверяемая гипотеза о согласии отвергается.
г) Критерий 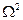 Мизеса
Мизеса
Вычисляем
значение статистики 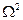 Мизеса
по формуле:
Мизеса
по формуле:
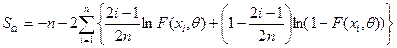
Составляем
расчетную таблицу:
|
i
|
xi
|
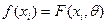
|
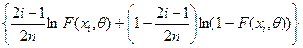
|
|
1
|
14,7
|
0,535
|
-0,75194
|
|
2
|
14,07
|
0,980
|
-3,148
|
|
3
|
14,16
|
0,866
|
-1,44833
|
|
4
|
14,53
|
0,593
|
-0,7482
|
|
5
|
15,01
|
0,499
|
-0,69315
|
|
6
|
14,31
|
0,724
|
-0,70844
|
|
7
|
14,83
|
0,510
|
-0,6852
|
|
8
|
15,31
|
0,538
|
-0,65068
|
|
9
|
15,32
|
0,540
|
-0,63172
|
|
10
|
14,88
|
0,504
|
-0,68429
|
|
сумма
|
-10,1499
|
Получаем:
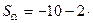 (-10,15)= 10,3. Для уровня
значимости
(-10,15)= 10,3. Для уровня
значимости 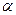 = 0.05 критическое значение статистики
= 0.05 критическое значение статистики 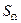 равно 2,4924.
равно 2,4924.
Так
как вычисленное по выборке значение статистики
превышает критическое, то проверяемая гипотеза о согласии отвергается.
Как видим, при задании уровня
значимости
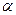 = 0.05 нет
оснований для
= 0.05 нет
оснований для
принятияия
проверяемой гипотезы по всем критериям согласия.