Вариант 8
1.
Найти среднее арифметическое, медиану, моду, среднее геометрическое, размах,
среднее квадратическое отклонение, дисперсию,
коэффициент вариации.
2. Построить гистограмму,
предварительно разбив выборку на 5 интервалов.
3. Осуществить проверку гипотезы о
среднем значении нормально распределенной генеральной совокупности при
известной дисперсии.
4. Осуществить проверку гипотезы о
среднем значении нормально распределенной генеральной совокупности при
неизвестной дисперсии.
5. Осуществить проверку гипотезы о
дисперсии нормально распределенной генеральной совокупности.
6. Осуществить проверку гипотезы о
согласии с нормальным распределением с параметром сдвига 15, параметром
масштаба 0,8 с использованием критерия 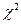 Пирсона.
Пирсона.
7. По выборке из первых 10 наблюдений
осуществить проверку гипотезы о согласии с нормальным распределением с
параметром сдвига 15, параметром масштаба 0,8 с использованием
непараметрических критериев Колмогорова, Смирнова, 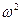 ,
, 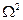 , Мизеса.
, Мизеса.
|
6,67
|
4,97
|
5,36
|
7,17
|
0,68
|
5,19
|
7,72
|
13,14
|
8,79
|
8,84
|
|
3,91
|
7,27
|
12,77
|
4,98
|
13,76
|
9,73
|
8,4
|
3,54
|
10,57
|
8,78
|
|
4,34
|
9,37
|
1,59
|
11,22
|
14,03
|
11,29
|
9,18
|
1,80
|
7,45
|
9,11
|
|
5,93
|
9,41
|
6,26
|
8,63
|
-1,06
|
11,21
|
3,78
|
3,41
|
11,02
|
5,71
|
|
8,03
|
7,47
|
5,99
|
3,28
|
9,30
|
6,14
|
6,54
|
11,02
|
8,03
|
7,42
|
Решение.
1.
Чтобы найти среднее
арифметическое, медиану, моду, размах, среднее квадратическое
отклонение, дисперсию, коэффициент вариации используем описательную статистику
в редакторе ЕXCEL:
|
Описательная статистика
|
|
Среднее
|
7,425
|
|
Стандартная ошибка
|
0,462
|
|
Медиана
|
7,460
|
|
Мода
|
8,030
|
|
Стандартное отклонение
|
3,270
|
|
Дисперсия выборки
|
10,694
|
|
Эксцесс
|
-0,413
|
|
Асимметричность
|
-0,058
|
|
Интервал
|
13,350
|
|
Минимум
|
0,680
|
|
Максимум
|
14,030
|
|
Сумма
|
371,260
|
|
Счет
|
50,000
|
Получаем:
среднее арифметическое - 7,425,
медиана - 7,460,
мода - 8,030,
размах - 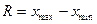 = 13,350,
= 13,350,
среднее квадратическое
отклонение - 3,270,
дисперсия - 10,694.
Коэффициент вариации 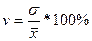 = 3,27 / 7,425 * 100 =
44,04%.
= 3,27 / 7,425 * 100 =
44,04%.
Среднее геометрическое  = 6,43.
= 6,43.
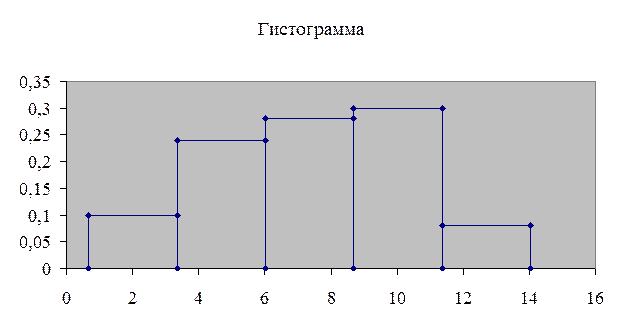
2. Разбиваем выборку на 5 интервалов.
При n=5 получаем
размер интервала 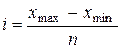 = 13,35/5= 2,67.
= 13,35/5= 2,67.
Находим границы
интервалов и считаем количество точек в каждом интервале:
|
№ интервала
|
Левая граница
|
Правая граница
|
Количество точек интервала
|
Частота
|
|
1-й интервал
|
0,68
|
3,35
|
5
|
0,1
|
|
2-й интервал
|
3,35
|
6,02
|
12
|
0,24
|
|
3-й интервал
|
6,02
|
8,69
|
14
|
0,28
|
|
4-й интервал
|
8,69
|
11,36
|
15
|
0,3
|
|
5-й интервал
|
11,36
|
14,03
|
4
|
0,08
|
3. Осуществим проверку гипотезы о
среднем значении 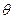 нормально
распределенной генеральной совокупности при известной дисперсии.
нормально
распределенной генеральной совокупности при известной дисперсии.
Гипотеза: 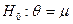 . Для
проверки такой гипотезы воспользуемся
критерием, статистика которого имеет вид:
. Для
проверки такой гипотезы воспользуемся
критерием, статистика которого имеет вид: 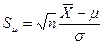 .
.
Пусть 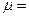 7, известная дисперсия
7, известная дисперсия 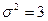 . Тогда
. Тогда 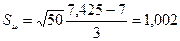 .
.
Критическое
значение статистики 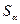 при уровне значимости
при уровне значимости 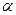 = 0.05 равно 1.645. Так как вычисленное по выборке
значение статистики не превышает критического, то проверяемая гипотеза о
согласии не отвергается.
= 0.05 равно 1.645. Так как вычисленное по выборке
значение статистики не превышает критического, то проверяемая гипотеза о
согласии не отвергается.
4.
Осуществим проверку гипотезы о среднем значении 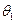 нормально
распределенной генеральной совокупности при неизвестной дисперсии.
нормально
распределенной генеральной совокупности при неизвестной дисперсии.
Гипотеза: 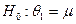 . Для
проверки такой гипотезы воспользуемся
критерием, статистика которого имеет вид:
. Для
проверки такой гипотезы воспользуемся
критерием, статистика которого имеет вид: 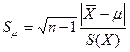 .
.
Пусть 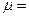 7. Тогда
7. Тогда 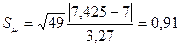 .
.
Критическое значение статистики 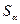 при уровне значимости
при уровне значимости 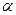 = 0.05 равно 1.67. Так как вычисленное по выборке
значение статистики не превышает критического, то проверяемая гипотеза о
согласии не отвергается.
= 0.05 равно 1.67. Так как вычисленное по выборке
значение статистики не превышает критического, то проверяемая гипотеза о
согласии не отвергается.
5.
Осуществим проверку гипотезы о дисперсии нормально распределенной генеральной
совокупности.
Гипотеза: 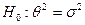 . Для
проверки такой гипотезы воспользуемся
критерием, статистика которого имеет вид:
. Для
проверки такой гипотезы воспользуемся
критерием, статистика которого имеет вид: 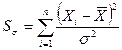 .
.
Составляем таблицу значений 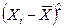 =
=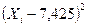
|
0,570
|
6,028
|
4,265
|
0,065
|
45,498
|
4,996
|
0,087
|
32,659
|
1,863
|
2,002
|
|
12,357
|
0,024
|
28,567
|
5,979
|
40,130
|
5,312
|
0,950
|
15,095
|
9,890
|
1,835
|
|
9,518
|
3,782
|
34,050
|
14,401
|
43,623
|
14,937
|
3,079
|
31,643
|
0,001
|
2,839
|
|
2,236
|
3,939
|
1,358
|
1,452
|
71,999
|
14,325
|
13,287
|
16,122
|
12,923
|
2,942
|
|
0,366
|
0,002
|
2,060
|
17,183
|
3,515
|
1,652
|
0,784
|
12,923
|
0,366
|
0,000
|
Тогда 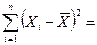 555,474.
555,474.
Пусть 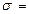 3. Тогда
3. Тогда 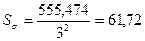 .
.
Критическое
значение статистики 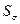 при уровне значимости
при уровне значимости 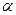 = 0.05 равно 67,5. Так как вычисленное по выборке
значение статистики не превышает критическое, то проверяемая гипотеза о
согласии не отвергается.
= 0.05 равно 67,5. Так как вычисленное по выборке
значение статистики не превышает критическое, то проверяемая гипотеза о
согласии не отвергается.
6. Осуществим проверку гипотезы о
согласии с нормальным распределением с использованием критерия 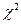 Пирсона.
Пирсона.
Гипотеза: 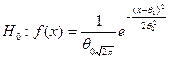 , где полагаем
, где полагаем 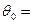 3,
3, 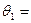 7.
7.
Для
вычисления значения статистики 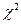 Пирсона по формуле
Пирсона по формуле
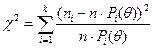
воспользуемся
результатом, полученным в п.2 при разбиении области определения
случайной величины на 5
интервалов группирования.
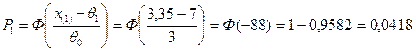 ,
,
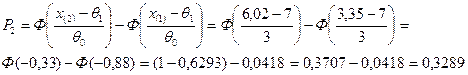 ,
,
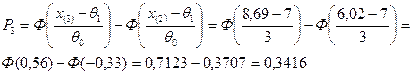 ,
,
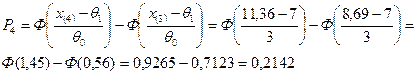
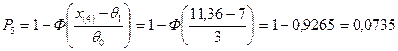 .
.
Получаем
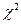 =7,556.
=7,556.
Для
уровня значимости 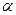 = 0.05 и
k
=5
критическое значение статистики
= 0.05 и
k
=5
критическое значение статистики 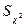 равно 9,4877.
равно 9,4877.
Сравниваем полученное значение 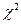 с
критическим значением статистики.. Так как вычисленное по выборке значение
статистики не превышает критического, то проверяемая гипотеза о согласии не
отвергается.
с
критическим значением статистики.. Так как вычисленное по выборке значение
статистики не превышает критического, то проверяемая гипотеза о согласии не
отвергается.
7. По выборке из первых 10 наблюдений
|
6,67
|
4,97
|
|
3,91
|
7,27
|
|
4,34
|
9,37
|
|
5,93
|
9,41
|
|
8,03
|
7,47
|
осуществим
проверку гипотезы о согласии с нормальным распределением с параметром сдвига
15, параметром масштаба 0,8 с использованием непараметрических критериев
Колмогорова, Смирнова, 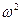 ,
, 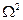 , Мизеса.
, Мизеса.
Гипотеза: 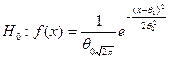 , где
, где 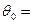 3,
3, 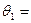 7.
7.
а)
Критерий Колмогорова
Вычисляем
значение статистики Колмогорова по формуле: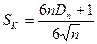 , где
, где 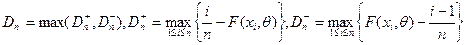 .
.
Составляем
расчетную таблицу:
|
i
|
xi
|
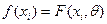
|
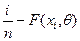
|
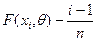
|
|
1
|
6,67
|
0,134
|
-0,034
|
0,134
|
|
2
|
3,91
|
0,226
|
-0,026
|
0,126
|
|
3
|
4,34
|
0,197
|
0,103
|
-0,003
|
|
4
|
5,93
|
0,142
|
0,258
|
-0,158
|
|
5
|
8,03
|
0,141
|
0,359
|
-0,259
|
|
6
|
4,97
|
0,167
|
0,433
|
-0,333
|
|
7
|
7,27
|
0,134
|
0,566
|
-0,466
|
|
8
|
9,37
|
0,182
|
0,618
|
-0,518
|
|
9
|
9,41
|
0,184
|
0,716
|
-0,616
|
|
10
|
7,47
|
0,135
|
0,865
|
-0,765
|
|
max
|
0,865
|
0,134
|
Получаем:
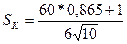 = 2,788.
= 2,788.
Для
уровня значимости 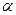 = 0.05 критическое значение статистики
= 0.05 критическое значение статистики 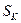 равно 1,3581.
равно 1,3581.
Так
как вычисленное по выборке значение статистики
превышает критическое, то проверяемая гипотеза о согласии отвергается.
б)
Критерий Смирнова
Вычисляем значение статистики Смирнова по
формуле 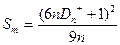
Получаем:
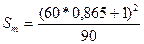 = 31,1.
= 31,1.
Для
уровня значимости 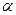 = 0.05 критическое значение статистики
= 0.05 критическое значение статистики 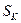 равно 5,9915.
равно 5,9915.
Так
как вычисленное по выборке значение статистики
превышает критическое, то проверяемая гипотеза о согласии отвергается.
в)
Критерий 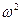 Мизеса.
Мизеса.
Вычисляем
значение статистики 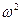 Мизеса
по формуле:
Мизеса
по формуле:
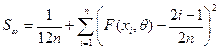
Составляем
расчетную таблицу:
|
i
|
xi
|
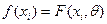
|
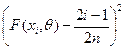
|
|
1
|
6,67
|
0,134
|
0,007
|
|
2
|
3,91
|
0,226
|
0,006
|
|
3
|
4,34
|
0,197
|
0,003
|
|
4
|
5,93
|
0,142
|
0,043
|
|
5
|
8,03
|
0,141
|
0,095
|
|
6
|
4,97
|
0,167
|
0,147
|
|
7
|
7,27
|
0,134
|
0,267
|
|
8
|
9,37
|
0,182
|
0,323
|
|
9
|
9,41
|
0,184
|
0,444
|
|
10
|
7,47
|
0,135
|
0,665
|
|
сумма
|
1,999
|
Получаем:
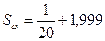 = 2,049.
= 2,049.
Для
уровня значимости 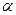 = 0.05 критическое значение статистики
= 0.05 критическое значение статистики 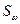 равно 0,4615.
равно 0,4615.
Так
как вычисленное по выборке значение статистики
превышает критическое, то проверяемая гипотеза о согласии отвергается.
г) Критерий 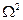 Мизеса
Мизеса
Вычисляем
значение статистики 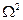 Мизеса
по формуле:
Мизеса
по формуле:
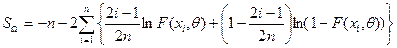
Составляем
расчетную таблицу:
|
i
|
xi
|
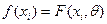
|
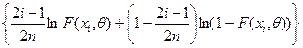
|
|
1
|
6,67
|
0,1
|
-0,33042
|
|
2
|
3,91
|
0,2
|
-0,5024
|
|
3
|
4,34
|
0,3
|
-0,6409
|
|
4
|
5,93
|
0,4
|
-0,87319
|
|
5
|
8,03
|
0,5
|
-1,05522
|
|
6
|
4,97
|
0,6
|
-1,14622
|
|
7
|
7,27
|
0,7
|
-1,45228
|
|
8
|
9,37
|
0,8
|
-1,40431
|
|
9
|
9,41
|
0,9
|
-1,54546
|
|
10
|
7,47
|
1
|
-2,00503
|
|
сумма
|
-10,9554
|
Получаем:
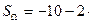 (-10,9554)= 11,91. Для уровня
значимости
(-10,9554)= 11,91. Для уровня
значимости 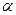 = 0.05 критическое значение статистики
= 0.05 критическое значение статистики 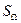 равно 2,4924.
равно 2,4924.
Так
как вычисленное по выборке значение статистики
превышает критическое, то проверяемая гипотеза о согласии отвергается.
Как видим, при задании уровня
значимости
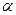 = 0.05 нет
оснований для
= 0.05 нет
оснований для
принятияия проверяемой
гипотезы по всем критериям согласия.