ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

Филиал в г. Уфе

Лабораторная работа

по дисциплине «ЭММ и ПМ»

Вариант 3

                                                               Выполнила:

.

                                                                                                     Проверил

                                                                 Уфа, 2007 г.

Лабораторная работа №1

Вариант №3

Задача линейного программирования

Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии –  60 изделий, второй линии – 75 изделий. На радиоприемник первой модели расходуется 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одного радиоприемника первой и второй моделей равны 30 и 20 ден. ед. соответственно. Определите оптимальные суточные объемы производства первой и второй моделей, чтобы прибыль была максимальной.  

   Экономико-математическая модель

Обозначим через Х1,Х2 суточный объем производства (количество моделей радиоприемников).

Целевая функция – этой математическая запись критерия оптимальности, то есть, выражение, которое необходимо максимизировать

                             f(х) = 30Х1 + 20Х2

Ограничения по продукции:

10Х1 + 8Х2 <= 800

Х1 <= 60

Х2 <= 75

Решение: 

1.                Создать форму для ввода условий задачи. Запустим Excel, выбрав Microsoft  Excel из подменю Программы главного меню Windows. Открывается чистый лист Excel.Создадим текстовую форму – таблицу для ввода условий задачи (рис 1)

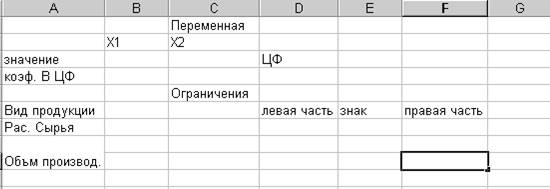
                                                   Рис.1

2. Укажим адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки). Обозначим через Х1, Х2 количество моделей радиоприемников. В нашей задаче оптимальные значения компонентов вектора Х = (Х1, Х2) будут помещены  в ячейках В3:С3, оптимальное значение целевой функции – в ячейки F3.

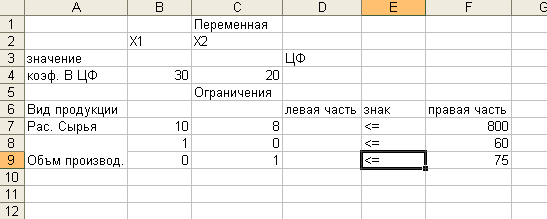
Рис.2

3.  Введем исходные данные задачи в созданную форму – таблицу, представленную на рис.2.

 4. Введем  зависимость для целевой функции:

-         курсор в ячейку  F4;

-         курсор на кнопку «Мастер функций», расположенную на панели инструментов;

-          на экране появляется диалоговое окно Мастер функций шаг 1 из 2;

-         курсор в окно «Категория» на категорию Математические;

-         курсор в окно Функции на СУММПРОИЗВ;

-         на экране появляется диалоговое окно СУММПРОИЗВ;

-         в строку «Массив 1» ввести В$3 : С$3;

-         в строку «Массив 2» ввести В4 : С4 ;

-         Кнопка «ОК». На экране: в ячейку F4 введена функция.

Рис.3

5. Введем  зависимость для ограничений:

-         курсор в ячейку D4;

-         на панели инструментов кнопка Копировать в буфер D7;

-         Курсор в ячейку D7;

-         на панели инструментов кнопка Вставить из буфераD8;

-         Курсор в ячейку D8;

-         на панели инструментов кнопка Вставить из буфера;

-         курсор в ячейку D9;

-         на панели инструментов кнопка Вставить из буфера.

    В строке Меню указатель мыши на имя Сервис. В развернутом меню команда Поиск решения. Появляется диалоговое окно Поиск решения (рис.4)

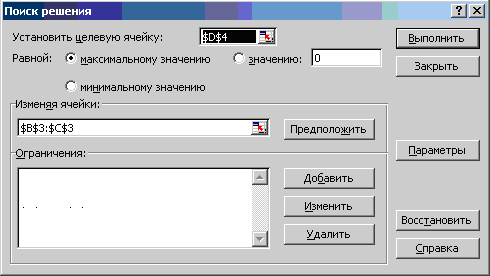
Рис.4

6. Назначить целевую функцию (установить целевую ячейку):

-         курсор в строку Установить целевую ячейку;

-         введем адрес ячейки $ D$ 4;

-         введите направление целевой функции в зависимости от условия вашей задачи – (Максимальному значению);

-         курсор в строку Изменяя ячейки;

-         введите адреса искомых переменных В$3 : C$3.

7. Введем ограничения:

-         указатель мышки на кнопку Добавить. Появляется диалоговое окно Добавление ограничения (рис.5);

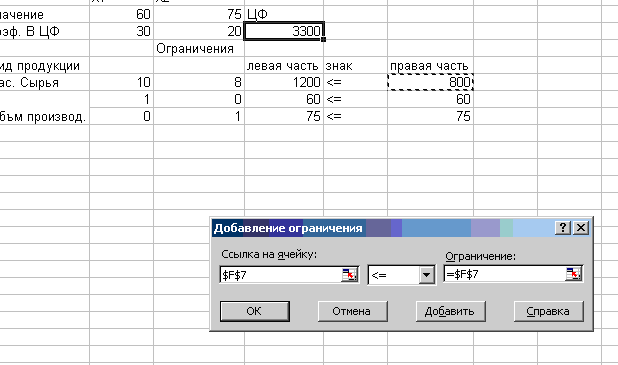
-         в строке Ссылка на ячейку введите адрес $ D$ 7;

-         введите знак ограничения <=;

-         в строке Ограничение введите адрес $ F $ 7;

-         указатель мыши на кнопку Добавить . На экране вновь диалоговое окно Добавление ограничения (рис.5);

-         введем  остальные ограничения задачи, по вышеописанному алгоритму;

-         после введения последнего ограничения кнопка ОК.

На экране появится диалоговое окно Поиск решения с введенными условиями (рис.6).

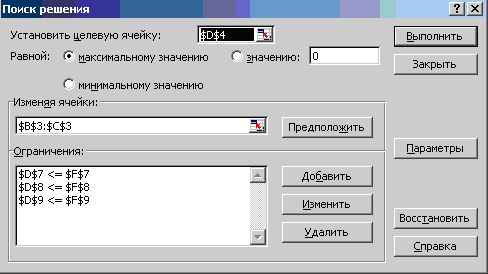
Рис.6

8. Введем параметры для решения задач линейного программирования:

-         в диалоговом окне указатель мыши на кнопку Параметры. На экране появляется диалоговое окно Параметры поиска решения.

-         установим флажки в окнах Линейная модель ( это обеспечит применение симплекс-метода) и Неотрицательные значения;

-         указатель мыши на кнопку ОК. На экране диалоговое окно Поиск решения;

-         указатель мыши на кнопку Выполнить.

Через непродолжительное время появится диалоговое окно Результаты

поиска решения и исходная таблица с заполненными ячейками В3 : C3 для значений Хi и ячейка D4 с максимальным значением целевой функции (рис.7)

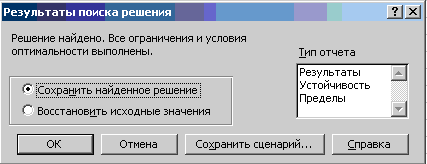
Рис.7

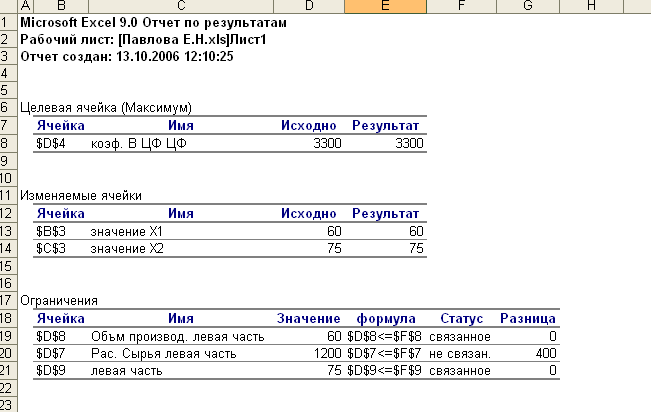
Создание отчета по результатам поиска решения.

EXCEL позволяет представить результатам поиска решения в форме отчета.

Вариант №3

Задача №2