Задание
Фирма рассматривает два варианта осуществления инвестиций,
различающихся вероятностями получения дохода. Вероятности получения дохода по
вариантам инвестиций представлены в таблице:
|
Варианты инвестиций
|
Размер
чистой прибыли в у.е.
|
|
-3
|
-2
|
-1
|
0
|
1
|
2
|
3
|
4
|
|
«А»
|
0
|
0
|
01
|
02
|
03
|
02
|
02
|
0
|
|
«Б»
|
0,1
|
0,1
|
0,1
|
0,1
|
0,1
|
0,1
|
0,2
|
0,2
|
Определить размер ожидаемой прибыли по инвестиционным
альтернативам. Оценить степень риска по
размеру стандартного отклонения и коэффициента вариации.
Решение.
Для значений размера чистой прибыли введем обозначение xi, для вероятностей введем обозначение pi.
Коэффициент вариации используют для сравнения рассеивания двух и более признаков,
имеющих различные единицы измерения. Коэффициент вариации представляет собой
относительную меру рассеивания, выраженную в процентах. Он вычисляется по
формуле:
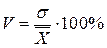 ,
,
где V – коэффициент вариации, s стандартное отклонение, 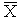 - средняя
величина (математическое ожидание чистой прибыли).
- средняя
величина (математическое ожидание чистой прибыли).
Средняя величина 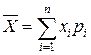 , где п – объем
выборки.
, где п – объем
выборки.
Стандартное
отклонение 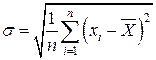 .
.
Для
каждого из вариантов вычисления организуем в вспомогательных таблицах.
Для
варианта «А»:
|
xi
|
pi
|
xi×pi
|
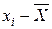
|
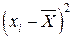
|
|
-3
|
0
|
0
|
-4.2
|
17.64
|
|
-2
|
0
|
0
|
-3.2
|
10.24
|
|
-1
|
0.1
|
-0.1
|
-2.2
|
4.84
|
|
0
|
0.2
|
0
|
-1.2
|
1.44
|
|
1
|
0.3
|
0.3
|
-0.2
|
0.04
|
|
2
|
0.2
|
0.4
|
0.8
|
0.64
|
|
3
|
0.2
|
0.6
|
1.8
|
3.24
|
|
4
|
0
|
0
|
2.8
|
7.84
|
|
Сумма
|
1
|
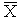 =1.2 =1.2
|
|
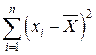 = 45.92 = 45.92
|
Средняя
величина (математическое ожидание) чистой прибыли 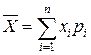 =1.2 у.е.
=1.2 у.е.
Стандартное
отклонение 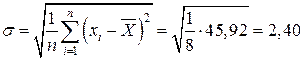 у.е..
у.е..
Коэффициент
вариации 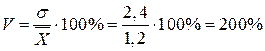 .
.
Для
варианта «Б»:
|
xi
|
pi
|
xi×pi
|
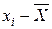
|
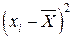
|
|
-3
|
0.1
|
-0.3
|
-4.1
|
16.81
|
|
-2
|
0.1
|
-0.2
|
-3.1
|
9.61
|
|
-1
|
0.1
|
-0.1
|
-2.1
|
4.41
|
|
0
|
0.1
|
0
|
-1.1
|
1.21
|
|
1
|
0.1
|
0.1
|
-0.1
|
0.01
|
|
2
|
0.1
|
0.2
|
0.9
|
0.81
|
|
3
|
0.2
|
0.6
|
1.9
|
3.61
|
|
4
|
0.2
|
0.8
|
2.9
|
8.41
|
|
Сумма
|
1
|
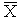 =1.1 =1.1
|
|
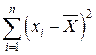 = 44.88 = 44.88
|
Средняя
величина (математическое ожидание) чистой прибыли 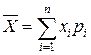 =1.1 у.е.
=1.1 у.е.
Стандартное
отклонение 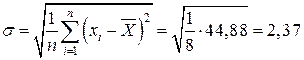 у.е..
у.е..
Коэффициент
вариации 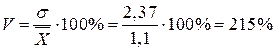 .
.
В
результате необходимо сделать тот вывод, что первый вариант инвестиций
предпочтительнее, т.к. ниже степень риска (стандартное отклонение, конечно,
больше у варианта «А», зато коэффициент вариации значительно ниже), а ожидаемый
доход в случае выбора варианта «А» выше.