Всероссийский заочный
финансово-экономический институт
Контрольная работа
по дисциплине «Эконометрика»
10 вариант
Выполнила:
Специальность: Финансы и кредит
Отделение: Заочное
Курс:3
№
зачетной книжки:
Руководитель:
Калуга 2008
Задача 1
1. Найти
параметры уравнения линейной регрессии, дать экономическую интерпретацию
коэффициента регрессии.
Уравнение
линейной регрессии: 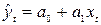 .
.
Система
нормальных уравнений:
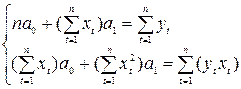
Таблица 1 Расчет параметров уравнения модели 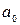 и
и 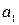
|
t
|
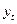
|
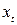
|
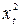
|
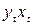
|
|
1
|
43
|
26
|
676
|
1118
|
|
2
|
28
|
18
|
324
|
504
|
|
3
|
51
|
33
|
1089
|
1683
|
|
4
|
62
|
42
|
1764
|
2604
|
|
5
|
63
|
41
|
1681
|
2583
|
|
6
|
67
|
44
|
1936
|
2948
|
|
7
|
26
|
15
|
225
|
390
|
|
8
|
43
|
27
|
729
|
1161
|
|
9
|
61
|
41
|
1681
|
2501
|
|
10
|
33
|
19
|
361
|
627
|
|
Сумма
|
477
|
306
|
10466
|
16119
|
|
Среднее значение
|
47,7
|
30,6
|
1046,6
|
1611,9
|
Подставим рассчитанные суммы в систему:
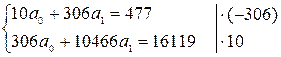
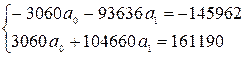
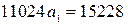
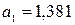
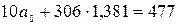
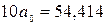
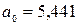
Линейная модель: 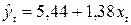 .
.
При увеличении объема
капиталовложений Х на 1 млн. руб., объем выпуска продукции Y возрастет на 1,38 млн. руб.
2. Вычислить
остатки; найти остаточную сумму квадратов; оценить дисперсию остатков;
построить график остатков.
Таблица 2 Расчет
остаточной суммы квадратов
|
t
|
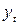
|
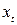
|
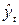
|
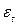
|
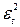
|
|
А
|
1
|
2
|
3
|
4
|
5
|
|
1
|
43
|
26
|
41,32
|
1,68
|
2,8224
|
|
2
|
28
|
18
|
30,28
|
-2,28
|
5,1984
|
|
3
|
51
|
33
|
50,98
|
0,02
|
0,0004
|
|
4
|
62
|
42
|
63,4
|
-1,40
|
1,9600
|
|
5
|
63
|
41
|
62,02
|
0,98
|
0,9604
|
|
6
|
67
|
44
|
66,16
|
0,84
|
0,7056
|
|
7
|
26
|
15
|
26,14
|
-0,14
|
0,0196
|
|
8
|
43
|
27
|
42,7
|
0,30
|
0,0900
|
|
9
|
61
|
41
|
62,02
|
-1,02
|
1,0404
|
|
10
|
33
|
19
|
31,66
|
1,34
|
1,7956
|
|
Сумма
|
477
|
306
|
476,68
|
0,32
|
14,5928
|
Остатки вычислены в графе 4.
Сумма квадратов остатков: 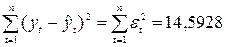 .
.
Дисперсия остатков:
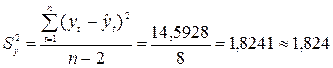 .
.
Рисунок 1
График остатков
3. Проверить
предпосылки МНК.
Таблица 3 Проверка
выполнения четырех свойств
|
t
|
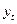
|
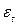
|
т
|
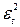
|
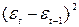
|
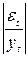
|
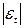
|
|
1
|
43
|
1,68
|
-
|
2,8224
|
-
|
0,0391
|
1,68
|
|
2
|
28
|
-2,28
|
1
|
5,1984
|
15,6816
|
0,0814
|
2,28
|
|
3
|
51
|
0,02
|
1
|
0,0004
|
5,2900
|
0,0004
|
0,02
|
|
4
|
62
|
-1,40
|
1
|
1,9600
|
2,0164
|
0,0226
|
1,40
|
|
5
|
63
|
0,98
|
1
|
0,9604
|
5,6644
|
0,0156
|
0,98
|
|
6
|
67
|
0,84
|
0
|
0,7056
|
0,0196
|
0,0125
|
0,84
|
|
7
|
26
|
-0,14
|
1
|
0,0196
|
0,9604
|
0,0054
|
0,14
|
|
8
|
43
|
0,30
|
1
|
0,0900
|
0,1936
|
0,0070
|
0,30
|
|
9
|
61
|
-1,02
|
1
|
1,0404
|
1,7424
|
0,0167
|
1,02
|
|
10
|
33
|
1,34
|
-
|
1,7956
|
5,5696
|
0,0406
|
1,34
|
|
Сумма
|
477
|
0,32
|
7
|
14,5928
|
37,1380
|
0,2413
|
10,00
|
1) Критерий поворотных точек:
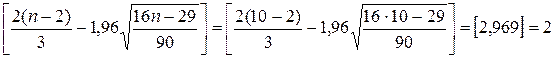 .
.
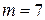 .
.
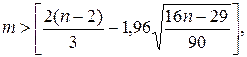
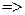 свойство
выполняется.
свойство
выполняется.
2) Проверка
независимости значений уровней случайной компоненты (критерий Дарбина-Уотсона):
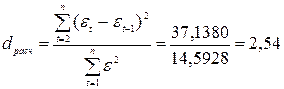 .
.
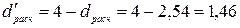 .
.
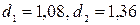 .
.
Т.к. 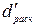 больше верхнего
табличного
больше верхнего
табличного 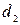
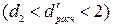 , свойство выполняется, автокорреляция отсутствует.
, свойство выполняется, автокорреляция отсутствует.
3) 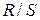 -критерий:
-критерий:
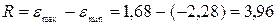 .
.
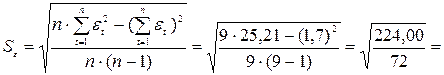
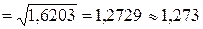 .
.
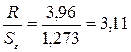 .
.
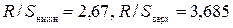 .
.
Т.к. значение 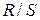 попадает в интервал
между нижней и верхней границами
попадает в интервал
между нижней и верхней границами 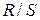 ,
, 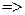 свойство
выполняется.
свойство
выполняется.
4) Проверка
равенства математического ожидания случайной компоненты нулю  :
:
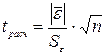 .
.
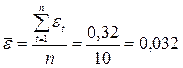 .
.
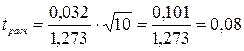 .
.
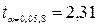 .
.
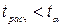 , свойство выполняется.
, свойство выполняется.
Уравнение модели 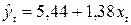 является адекватным,
т.к. все свойства выполняются.
является адекватным,
т.к. все свойства выполняются.
4. Вычислить
коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера (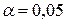 ), найти среднюю относительную ошибку аппроксимации.
), найти среднюю относительную ошибку аппроксимации.
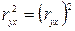 .
.
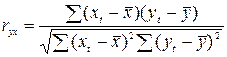
Таблица 4 Расчет коэффициента корреляции
|
t
|
yt
|
хt
|
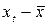
|
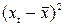
|
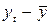
|
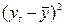
|
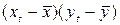
|
|
1
|
43
|
26
|
-4,6
|
21,16
|
-4,7
|
22,09
|
21,62
|
|
2
|
28
|
18
|
-12,6
|
158,76
|
-19,7
|
388,09
|
248,22
|
|
3
|
51
|
33
|
2,4
|
5,76
|
3,3
|
10,89
|
7,92
|
|
4
|
62
|
42
|
11,4
|
129,96
|
14,3
|
204,49
|
163,02
|
|
5
|
63
|
41
|
10,4
|
108,16
|
15,3
|
234,09
|
159,12
|
|
6
|
67
|
44
|
13,4
|
179,56
|
19,3
|
372,49
|
258,62
|
|
7
|
26
|
15
|
-15,6
|
243,36
|
-21,7
|
470,89
|
338,52
|
|
8
|
43
|
27
|
-3,6
|
12,96
|
-4,7
|
22,09
|
16,92
|
|
9
|
61
|
41
|
10,4
|
108,16
|
13,3
|
176,89
|
138,32
|
|
10
|
33
|
19
|
-11,6
|
134,56
|
-14,7
|
216,09
|
170,52
|
|
Сумма
|
477
|
306
|
0,0
|
1102,40
|
0,0
|
2118,10
|
1522,80
|
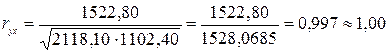 .
.
Связь между объемом выпуска продукции Х и объемом
капиталовложений Y
очень тесная и прямая. Значение коэффициента корреляции, равное единице,
свидетельствует о наличии функциональной связи между показателями.
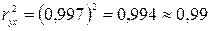 .
.
99% вариации объема выпуска продукции Y объясняется объемом капиталовложений
Х.
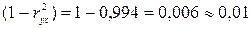 .
.
1% вариации объема выпуска продукции Y обусловлено факторами, не включенными
в модель.
F-критерий Фишера:
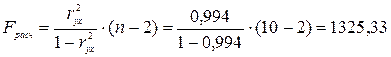 .
.
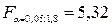 .
.
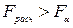 ,
, 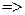 уравнение
регрессии значимо.
уравнение
регрессии значимо.
Средняя относительная ошибка аппроксимации:
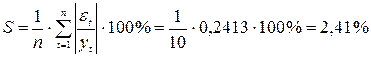 .
.
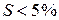 ,
, 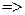 модель точная.
модель точная.
Средний модуль остатков:
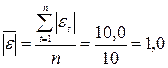 .
.
Стандартная ошибка отклонений:
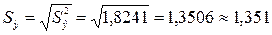 .
.
5. Осуществить
проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (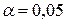 ). Сделать вывод о качестве модели.
). Сделать вывод о качестве модели.
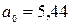 :
:
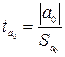 ;
; 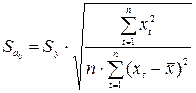 .
.
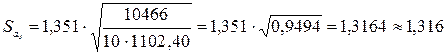 .
.
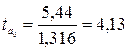 .
.
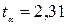 .
.
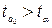 ,
, 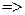
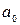 - значим.
- значим.
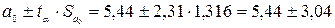 .
.
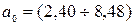 .
.
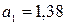 :
:
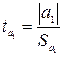 .
.
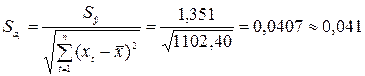 .
.
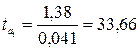 .
.
 ,
, 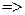
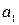 - значим.
- значим.
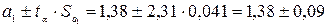 .
.
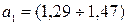 .
.
По всем показателям модель адекватная и точная, значит в
целом качественная.
6. Осуществить
прогнозирование среднего значения показателя Y при уровне значимости 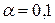 , если прогнозное значение фактора Х составит 80% от его
максимального значения.
, если прогнозное значение фактора Х составит 80% от его
максимального значения.
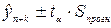
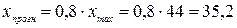 .
.
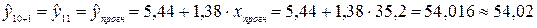 .
.
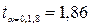 .
.
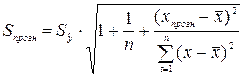 .
.
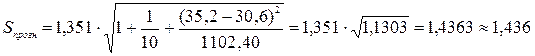 .
.
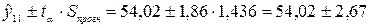 .
.
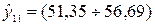 .
.
7. Представить графически:
фактические и модельные значения Y, точки прогноза.
Рисунок 2 График линейной модели
Рисунок 3
Прогноз по линейной модели
8. Составить
уравнения нелинейной регрессии:
1)
гиперболической;
2)
степенной;
3)
показательной.
Привести графики построенных уравнений регрессии.
1) Гиперболическая
регрессия: 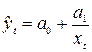 .
.
Система нормальных уравнений:
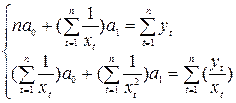
Составим расчетную таблицу.
Таблица 5 Расчет
параметров гиперболической регрессии
|
t
|
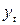
|
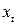
|
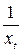
|
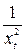
|
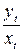
|
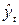
|
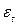
|
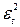
|
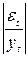
|
|
1
|
43
|
26
|
0,0385
|
0,0015
|
1,6538
|
46,9014
|
-3,9014
|
15,2209
|
0,0907
|
|
2
|
28
|
18
|
0,0556
|
0,0031
|
1,5556
|
31,0607
|
-3,0607
|
9,3679
|
0,1093
|
|
3
|
51
|
33
|
0,0303
|
0,0009
|
1,5455
|
54,4618
|
-3,4618
|
11,9841
|
0,0679
|
|
4
|
62
|
42
|
0,0238
|
0,0006
|
1,4762
|
60,4792
|
1,5208
|
2,3128
|
0,0245
|
|
5
|
63
|
41
|
0,0244
|
0,0006
|
1,5366
|
59,9410
|
3,0590
|
9,3575
|
0,0486
|
|
6
|
67
|
44
|
0,0227
|
0,0005
|
1,5227
|
61,4821
|
5,5179
|
30,4472
|
0,0824
|
|
7
|
26
|
15
|
0,0667
|
0,0044
|
1,7333
|
20,7643
|
5,2357
|
27,4126
|
0,2014
|
|
8
|
43
|
27
|
0,0370
|
0,0014
|
1,5926
|
48,2215
|
-5,2215
|
27,2641
|
0,1214
|
|
9
|
61
|
41
|
0,0244
|
0,0006
|
1,4878
|
59,9410
|
1,0590
|
1,1215
|
0,0174
|
|
10
|
33
|
19
|
0,0526
|
0,0028
|
1,7368
|
33,7703
|
-0,7703
|
0,5934
|
0,0233
|
Сумма
|
477
|
306
|
0,3760
|
0,0164
|
15,8409
|
477,0233
|
-0,0233
|
135,0820
|
0,7869
|
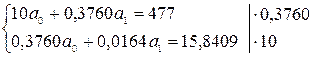
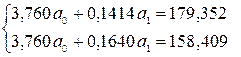
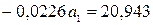
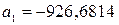
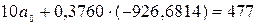
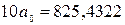
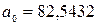
Гиперболическая
регрессия: 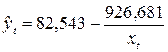
Асимптоты: 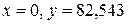 .
.
Рисунок 4 График гиперболической
модели
2) Степенная регрессия: 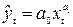 .
.
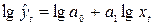
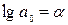
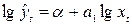
Система
нормальных уравнений:
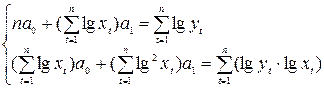
Таблица 6 Расчет параметров степенной модели
|
t
|
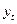
|
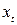
|
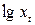
|
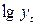
|
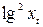
|
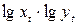
|
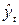
|
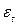
|
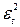
|
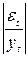
|
|
1
|
43
|
26
|
1,4150
|
1,6335
|
2,0022
|
2,3114
|
41,6493
|
1,3507
|
1,8244
|
0,0314
|
|
2
|
28
|
18
|
1,2553
|
1,4472
|
1,5758
|
1,8167
|
30,1461
|
-2,1461
|
4,6057
|
0,0766
|
|
3
|
51
|
33
|
1,5185
|
1,7076
|
2,3058
|
2,5930
|
51,3594
|
-0,3594
|
0,1292
|
0,0070
|
|
4
|
62
|
42
|
1,6232
|
1,7924
|
2,6348
|
2,9094
|
63,4867
|
-1,4867
|
2,2103
|
0,0240
|
|
5
|
63
|
41
|
1,6128
|
1,7993
|
2,6011
|
2,9019
|
62,1561
|
0,8439
|
0,7122
|
0,0134
|
|
6
|
67
|
44
|
1,6435
|
1,8261
|
2,7011
|
3,0012
|
66,1365
|
0,8635
|
0,7456
|
0,0129
|
|
7
|
26
|
15
|
1,1761
|
1,4150
|
1,3832
|
1,6642
|
25,6821
|
0,3179
|
0,1011
|
0,0122
|
|
8
|
43
|
27
|
1,4314
|
1,6335
|
2,0489
|
2,3382
|
43,0542
|
-0,0542
|
0,0029
|
0,0013
|
|
9
|
61
|
41
|
1,6128
|
1,7853
|
2,6011
|
2,8793
|
62,1561
|
-1,1561
|
1,3366
|
0,0190
|
|
10
|
33
|
19
|
1,2788
|
1,5185
|
1,6353
|
1,9419
|
31,6134
|
1,3866
|
1,9227
|
0,0420
|
|
Сумма
|
477
|
306
|
14,5674
|
16,5584
|
21,4894
|
24,3572
|
477,4399
|
-0,4399
|
13,5907
|
0,2398
|
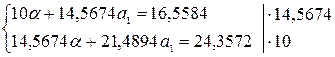
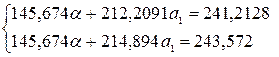
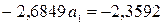
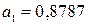
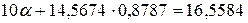
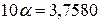
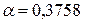
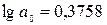
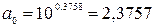
Степенная
регрессия: 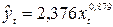 .
.
Рисунок 5 График по степенной
модели
3) Показательная регрессия: 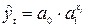 .
.
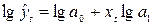
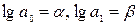
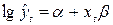
Система
нормальных уравнений:
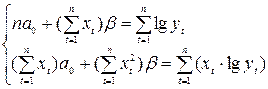
Расчеты
приведены в таблице 7.
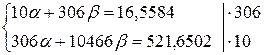


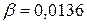
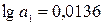
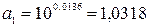
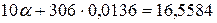
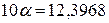
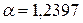
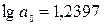
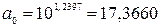
Показательная
модель: 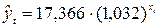
Таблица 7 Расчет параметров показательной
регрессии
|
t
|
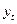
|
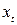
|
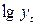
|
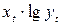
|
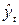
|
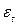
|
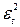
|
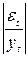
|
|
1
|
43
|
26
|
1,6335
|
42,4710
|
39,3887
|
3,6113
|
13,0415
|
0,0840
|
|
2
|
28
|
18
|
1,4472
|
26,0496
|
30,6150
|
-2,615
|
6,8382
|
0,0934
|
|
3
|
51
|
33
|
1,7076
|
56,3508
|
49,1055
|
1,8945
|
3,5891
|
0,0371
|
|
4
|
62
|
42
|
1,7924
|
75,2808
|
65,1999
|
-3,1999
|
10,2394
|
0,0516
|
|
5
|
63
|
41
|
1,7993
|
73,7713
|
63,1782
|
-0,1782
|
0,0318
|
0,0028
|
|
6
|
67
|
44
|
1,8261
|
80,3484
|
69,4395
|
-2,4395
|
5,9512
|
0,0364
|
|
7
|
26
|
15
|
1,4150
|
21,2250
|
27,8545
|
-1,8545
|
3,4392
|
0,0713
|
|
8
|
43
|
27
|
1,6335
|
44,1045
|
40,6492
|
2,3508
|
5,5263
|
0,0547
|
|
9
|
61
|
41
|
1,7853
|
73,1973
|
63,1782
|
-2,1782
|
4,7446
|
0,0357
|
|
10
|
33
|
19
|
1,5185
|
28,8515
|
31,5947
|
1,4053
|
1,9749
|
0,0426
|
|
Сумма
|
477
|
306
|
16,5584
|
521,6502
|
480,2034
|
-3,2034
|
55,3760
|
0,5096
|
Рисунок 6 График по показательной модели
9. Для
указанных моделей найти коэффициенты детерминации и средние относительные
ошибки аппроксимации. Сравнить модели по этим характеристикам.
1) Гиперболическая модель:
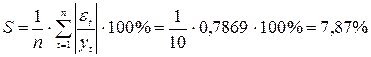 .
.
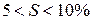 ,
, 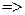 модель пригодна для
анализа.
модель пригодна для
анализа.
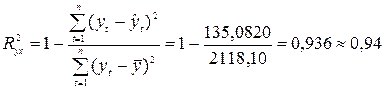 .
.
94%
вариации объема выпуска продукции Y
объясняется объемом капиталовложений Х.
2) Степенная модель:
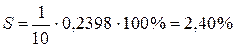 .
.
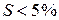 ,
, 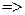 модель точная.
модель точная.
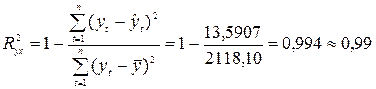 .
.
99%
вариации объема выпуска продукции Y
объясняется объемом капиталовложений Х.
3) Показательная модель:
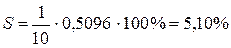 .
.
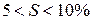 ,
, 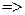 модель пригодна для
анализа.
модель пригодна для
анализа.
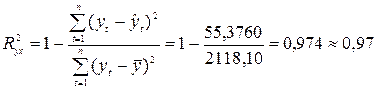 .
.
97%
вариации объема выпуска продукции Y
объясняется объемом капиталовложений Х.
Таблица 8 Сводная таблица результатов
Модель
|
Параметр
|
|
Коэффициент
детерминации, 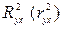
|
Средняя
относительная ошибка аппроксимации в %, S
|
|
Линейная
|
0,994
|
2,41
|
|
Гиперболическая
|
0,936
|
7,87
|
|
Степенная
|
0,994
|
2,40
|
|
Показательная
|
0,974
|
5,10
|
Лучшая модель – степенная.
Задача 2
Задача 2а и
2б. Даны две СФМ, которые заданы в виде матриц коэффициентов модели.
Необходимо записать системы одновременных уравнений и проверить обе системы на
идентифицируемость.
Таблица 9
Исходные данные
|
Номер уравнения
|
Задача 2а
|
Задача 2б
|
|
переменные
|
переменные
|
|
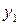
|
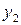
|
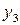
|
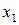
|
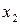
|
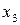
|
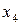
|
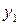
|
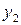
|
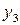
|
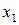
|
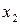
|
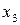
|
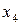
|
|
1
|
-1
|
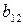
|
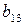
|
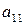
|
0
|
0
|

|
-1
|
0
|
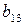
|
0
|
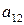
|
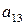
|

|
|
2
|
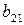
|
-1
|
0
|
0
|
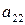
|
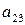
|
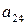
|
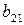
|
-1
|
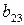
|
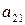
|
0
|
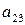
|
0
|
|
3
|
0
|
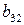
|
-1
|
0
|
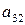
|
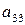
|
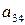
|
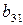
|
0
|
-1
|
0
|
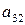
|
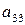
|
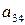
|
Задача 2а
Система
одновременных уравнений:
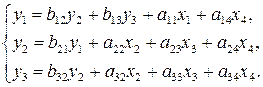
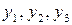 - эндогенные
переменные,
- эндогенные
переменные,
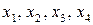 - экзогенные
переменные.
- экзогенные
переменные.
Проверим
каждое уравнение на идентифицируемость:
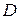 - число отсутствующих
экзогенных переменных в уравнении;
- число отсутствующих
экзогенных переменных в уравнении;
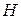 - число эндогенных
переменных в уравнении.
- число эндогенных
переменных в уравнении.
Первое
уравнение:
Необходимое условие: 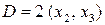 ,
, 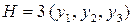 .
.
Выполняется
необходимое равенство: 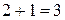 , следовательно, уравнение идентифицировано.
, следовательно, уравнение идентифицировано.
Достаточное условие:
|
Уравнение
|
Отсутствующие
переменные
|
|
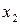
|
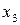
|
|
Второе
|
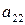
|
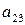
|
|
Третье
|
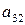
|
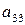
|
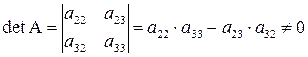 .
.
Ранг
матрицы:
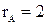 .
.
Достаточное
условие выполняется. Первое уравнение
идентифицировано.
Второе
уравнение:
Необходимое условие: 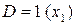 ,
, 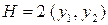 .
.
Выполняется
необходимое равенство: 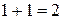 , следовательно, уравнение идентифицировано.
, следовательно, уравнение идентифицировано.
Достаточное условие:
|
Уравнение
|
Отсутствующие
переменные
|
|
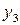
|
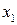
|
|
Первое
|
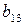
|
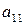
|
|
Третье
|
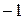
|
0
|
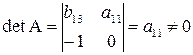 ;
;
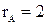 .
.
Достаточное
условие выполняется. Второе уравнение
идентифицировано.
Третье
уравнение:
Необходимое условие: 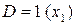 ,
, 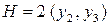 .
.
Выполняется
необходимое равенство: 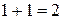 , следовательно, уравнение идентифицировано.
, следовательно, уравнение идентифицировано.
Достаточное условие:
|
Уравнение
|
Отсутствующие
переменные
|
|
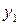
|
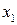
|
|
Первое
|
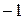
|
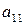
|
|
Второе
|
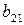
|
0
|
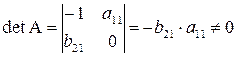 ;
;
 .
.
Достаточное
условие выполняется. Третье уравнение
идентифицировано.
СФМ
является идентифицируемой, т.к. все уравнения в системе идентифицируемы.
Задача 2б
Система
одновременных уравнений:
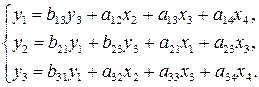
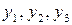 - эндогенные
переменные,
- эндогенные
переменные,
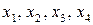 - экзогенные
переменные.
- экзогенные
переменные.
Проверим
каждое уравнение на идентифицируемость:
Первое
уравнение:
Необходимое условие: 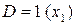 ,
, 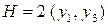 .
.
Выполняется
необходимое равенство: 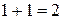 , следовательно, уравнение идентифицировано.
, следовательно, уравнение идентифицировано.
Достаточное условие:
|
Уравнение
|
Отсутствующие
переменные
|
|
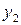
|
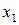
|
|
Второе
|
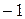
|
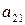
|
|
Третье
|
0
|
0
|
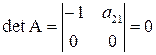 ;
;
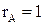 .
.
Достаточное
условие не выполняется. Первое уравнение
не является идентифицированным.
Второе
уравнение:
Необходимое условие: 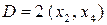 ,
, 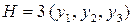 .
.
Выполняется
необходимое равенство: 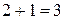 , следовательно, уравнение идентифицировано.
, следовательно, уравнение идентифицировано.
Достаточное условие:
|
Уравнение
|
Отсутствующие
переменные
|
|
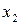
|
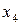
|
|
Первое
|
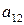
|

|
|
Третье
|
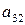
|
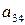
|
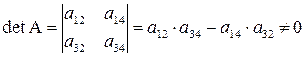 ;
;
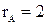 .
.
Достаточное
условие выполняется. Второе уравнение
идентифицировано.
Третье
уравнение:
Необходимое условие: 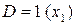 ,
, 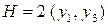 .
.
Выполняется
необходимое равенство: 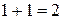 , следовательно, уравнение идентифицировано.
, следовательно, уравнение идентифицировано.
Достаточное условие:
|
Уравнение
|
Отсутствующие
переменные
|
|
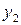
|
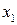
|
|
Первое
|
0
|
0
|
|
Второе
|
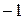
|
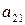
|
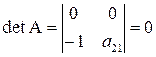 ;
;
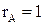 .
.
Достаточное
условие не выполняется. Третье уравнение
не является идентифицированным.
СФМ
не является идентифицируемой, т.к. не все уравнения идентифицируемы.
Задача 2в. Используя
косвенный метод наименьших квадратов, построить структурную форму модели вида
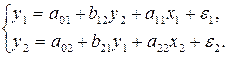
Таблица 10 Исходные
данные
|
t
|
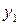
|
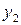
|
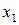
|
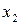
|
|
1
|
98,9
|
68,2
|
6
|
8
|
|
2
|
57,9
|
46,0
|
1
|
7
|
|
3
|
96,3
|
69,6
|
5
|
9
|
|
4
|
140,5
|
104,7
|
4
|
20
|
|
5
|
118,5
|
82,1
|
6
|
12
|
|
6
|
63,9
|
48,8
|
3
|
5
|
1. Составим
ПФМ:
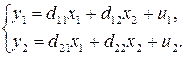
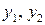 - эндогенные
переменные,
- эндогенные
переменные,
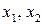 - экзогенные
переменные.
- экзогенные
переменные.
Для
упрощения расчетов найдем отклонения переменных от своих средних:
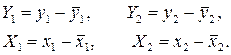
Таблица 11 Расчет
параметров ПФМ
|
t
|
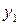
|
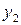
|
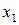
|
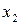
|
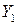
|
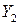
|
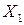
|
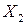
|
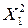
|
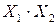
|
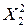
|
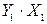
|
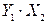
|
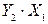
|
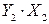
|
|
1
|
98,9
|
68,2
|
6
|
8
|
2,9
|
-1,7
|
1,833
|
-2,167
|
3,360
|
-3,972
|
4,696
|
5,316
|
-6,284
|
-3,116
|
3,684
|
|
2
|
57,9
|
46,0
|
1
|
7
|
-38,1
|
-23,9
|
-3,167
|
-3,167
|
10,030
|
10,030
|
10,030
|
120,663
|
120,663
|
75,691
|
75,691
|
|
3
|
96,3
|
69,6
|
5
|
9
|
0,3
|
-0,3
|
0,833
|
-1,167
|
0,694
|
-0,972
|
1,362
|
0,250
|
-0,350
|
-0,250
|
0,350
|
|
4
|
140,5
|
104,7
|
4
|
20
|
44,5
|
34,8
|
-0,167
|
9,833
|
0,028
|
-1,642
|
96,688
|
-7,431
|
437,569
|
-5,812
|
342,188
|
|
5
|
118,5
|
82,1
|
6
|
12
|
22,5
|
12,2
|
1,833
|
1,833
|
3,360
|
3,360
|
3,360
|
41,243
|
41,243
|
22,363
|
22,363
|
|
6
|
63,9
|
48,8
|
3
|
5
|
-32,1
|
-21,1
|
-1,167
|
-5,167
|
1,362
|
6,030
|
26,698
|
37,461
|
165,861
|
24,624
|
109,024
|
|
Сумма
|
576,0
|
419,4
|
25
|
61
|
0,0
|
0,0
|
-0,002
|
-0,002
|
18,834
|
12,834
|
142,834
|
197,502
|
758,702
|
113,500
|
553,300
|
Средние значения:
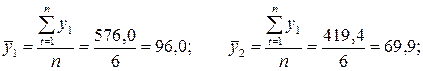
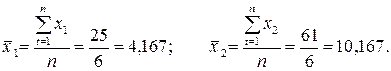
Первое уравнение: 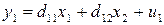 .
.
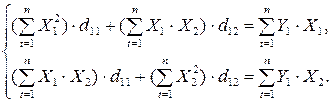
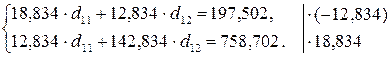
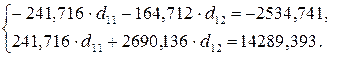

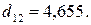
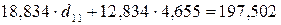
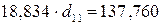
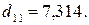
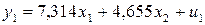 .
.
Второе уравнение: 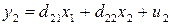 .
.
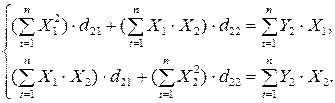
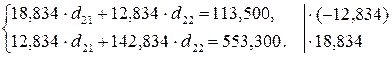
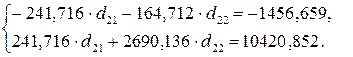
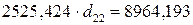
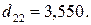
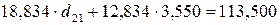
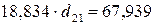

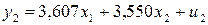 .
.
ПФМ: 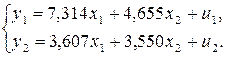
2. Путем алгебраических преобразований, перейдем от ПФМ
к СФМ:
Первое уравнение: 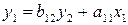 .
.
Выразим из
второго уравнения ПФМ 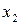 :
:
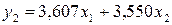
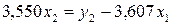
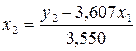 .
.
Подставим в
первое уравнение ПФМ:
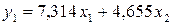
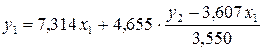
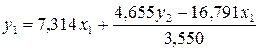
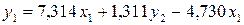
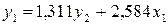 .
.
Отсюда, 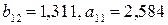 .
.
Второе уравнение: 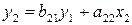 .
.
Выразим из
первого уравнения ПФМ 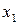 :
:
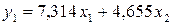
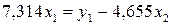
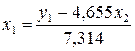 .
.
Подставим в
первое уравнение ПФМ:

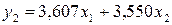
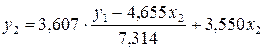
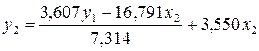
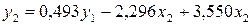
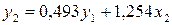
Отсюда, 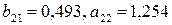 .
.
Найдем
свободные члены:
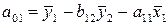 .
.
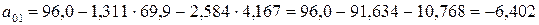 .
.
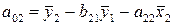 .
.
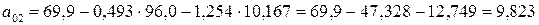 .
.
СФМ: