1. Найти среднее арифметическое, медиану, моду, среднее геометрическое, размах, среднее квадратическое отклонение, дисперсию, коэффициент вариации.

2. Построить гистограмму, предварительно разбив выборку на 5 интервалов.

3. Осуществить проверку гипотезы о среднем значении нормально распределенной генеральной совокупности при известной дисперсии.

4. Осуществить проверку гипотезы о среднем значении нормально распределенной генеральной совокупности при неизвестной дисперсии.

5. Осуществить проверку гипотезы о дисперсии нормально распределенной генеральной совокупности.

6. Осуществить проверку гипотезы о согласии с нормальным распределением с

параметром сдвига 15, параметром масштаба 0.8 с использованием критерия χ² Пирсона.

7. По выборке из первых 10 наблюдений осуществить проверку гипотезы о согласии с нормальным распределением с параметром сдвига 15, параметром масштаба 0.8 с

использованием непараметрических критериев Колмогорова, Смирнова, ω², Ω² Мизеса.

Решение

1. Найти среднее арифметическое, медиану, моду, среднее геометрическое, размах, среднее квадратическое отклонение, дисперсию, коэффициент вариации.

Среднее арифметическое.

Хср = ∑Хi/n

Где хi – число

n – количество чисел

Медиана

Ме = х_ме*i_мe*1/2∑f+1-S_me-1/f_me

Где хме – начало медианного интервала, ime – величина медианного интервала, Sme-1 – сумма накопленных частот в домедианном интервале.

Мода

Мо = х_мо+i_мо*f_mo-f_mo-1/( f_mo-f_mo-1)+( f_mo-f_mo+1)

Где хмо- нижняя граница модального интервала, imo – величина модального интервала. -f_mo-1,f_mo,f_mo+1 – частоты соответственно модального, домодального и послемодального интервалов.

Если множество данных не содержит одинаковых данных, то функция МОДА возвращает значение ошибки #Н/Д

Среднее геометрическое

СРГЕОМ = ⁿ√х₁*х₂*…*х₃

Размах

Размах = х_макс-х_мин

Среднее квадратическое отклонение

σ = 1/n∑х-хср

Дисперсия

σ²

Коэффициент вариации.

σ/х_ср *100

2. Построить гистограмму, предварительно разбив выборку на 5 интервалов.

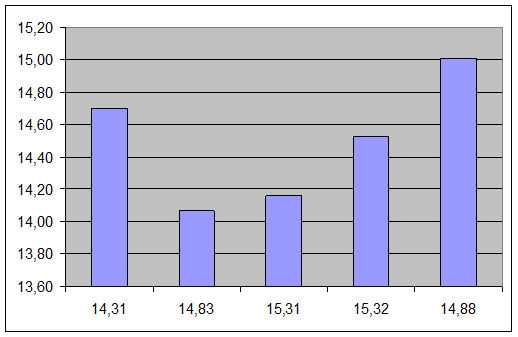
Гистограмма 1 интервала

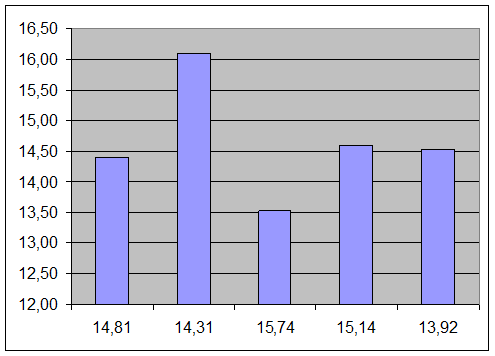
Гистограмма 2 интервала

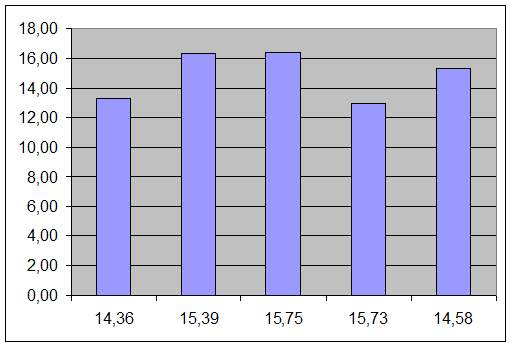
Гистограмма 3 интервала

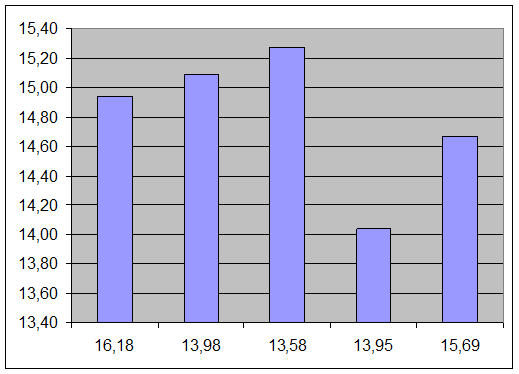
Гистограмма 4 интервала

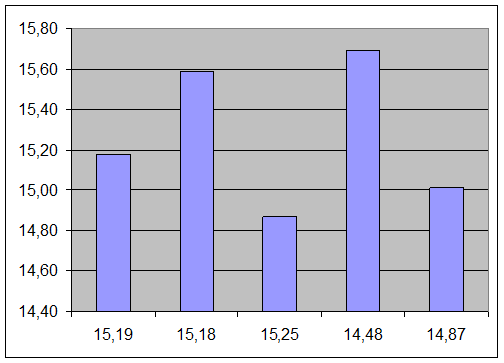
Гистограмма 5 интервала

3. Проверка гипотезы о среднем значении нормально распределенной генеральной совокупности при известной дисперсии

Пусть для нормально распределенной случайной величины ξ с известной дисперсией σ² и неизвестным средним θ необходимо проверить гипотезу: Н₀: θ = μ. Для проверки такой гипотезы можно воспользоваться критерием, статистика которого имеет вид:

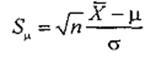
где n - объем выборки, Х- выборочное среднее (среднее арифметическое). Данная статистика при верности нулевой гипотезы подчиняется стандартному нормальному распределению: G(Sμ│H₀) = Ф(Sμ ).

Если вычисленное по выборке значение статистики не превышает критического, тогда проверяемая гипотеза о согласии не отвергается.

4. Проверка гипотезы о среднем значении нормально распределенной генеральной совокупности при неизвестной дисперсии

Пусть для нормально распределенной случайной величины ξ , с неизвестным средним θ₁, и неизвестной дисперсией θ₂² необходимо проверить гипотезу: Н₀: θ₁ = μ. Для проверки такой гипотезы можно воспользоваться критерием, статистика которого имеет вид:

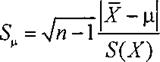
где n- объем выборки, X - выборочное среднее (среднее арифметическое), S(X) -среднее квадратическое отклонение. Данная статистика при верности нулевой гипотезы подчиняется t- распределению Стьюдента с n-1 степенями свободы.

Если вычисленное по выборке значение статистики не превышает критического, тогда проверяемая гипотеза о согласии не отвергается.

5. Проверка гипотезы о дисперсии нормально распределенной генеральной совокупности

Пусть для нормально распределенной случайной величины ξ, с известным математическим ожиданием μ. неизвестной дисперсией θ² необходимо проверить гипотезу: H₀: θ² = σ². Для проверки такой гипотезы можно воспользоваться критерием, статистика которого имеет вид:

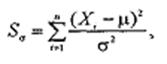
где n - объем выборки, Х - выборочное среднее (среднее арифметическое). Данная статистика при верности нулевой гипотезы подчиняется распределению хиквадрат с числом степеней свободы, равным п : G(S_σ │ H₀) = χ²(n).

Если вычисленное по выборке значение статистики не превышает критического, тогда проверяемая гипотеза о согласии не отвергается.

6. Осуществить проверку гипотезы о нормальном распределении генеральной совокупности с использованием критерия χ2 •

Проверяемая гипотеза имеет вид

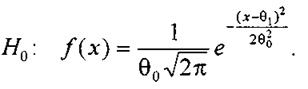
В качестве значений параметров θ_l и θ₀ следует выбрать среднее арифметическое и среднее квадратическое отклонение соответственно (см. п.1).

Для проверки данной гипотезы зададимся уровнем значимости а = 0.05

Для вычисления значения статистики χ² Пирсона по формуле

χ² = ∑(n_i-n*(P_i(θ))²/n* P_i(θ)

необходимо воспользоваться результатом, полученным в п.2 при разбиении области определения случайной величины на k = 5 интервалов группирования. Значения вероятностей попадания в интервалы группирования рассчитываются следующим образом (рассмотрим случай k = 5):

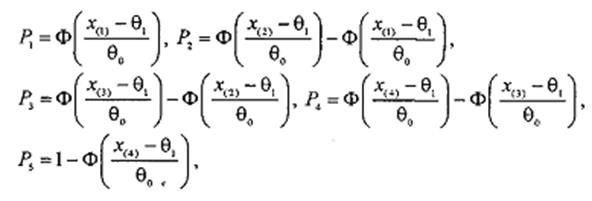
где x₍₁₎,. x₍₂₎,.х₍₃₎,.х_{4) - граничные точки (см. п.2), Ф(t) - стандартное нормальное распределение (см. таблицу 1).

Вычислив значение статистики х² Пирсона по формуле (1), необходимо сравнить полученное значение с критическим значением статистики. Для уровня значимости а = 0.05 и k = 5 критическое значение статистики S, равно 9,4877. Если вычисленное по выборке значение статистики не превышает критического, тогда проверяемая гипотеза о согласии не отвергается.

7. Осуществить проверку гипотезы о нормальном распределении генеральной совокупности с использованием непараметрических критериев Колмогорова, Смирнова, ω2, Ω2 Мизеса.

Проверяется простая гипотеза о принадлежности выборки нормаль­ному закону. Упорядоченная выборка объемом 100 наблюдений имеет вид: 1

Проверяемая гипотеза имеет вид

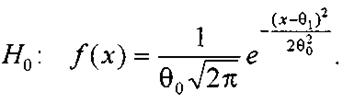
при значении параметра θ₀ = 0,5; θ₁ = 1. ;

Для проверки данной гипотезы зададимся уровнем значимости а = 0.05

A) Критерий Колмогорова

Вычисляем значение статистики Колмогорова по формуле :

S_K = 6*n*Dn+1/6√n

S_K =0,7410. Критическое значение статистики S_K при уровне значимости а = 0.05 равно, 1,3581. Поскольку полученное по выборке значение статистики не превышает критического, гипотеза о согласии с нормальным распределением с параметрами 0₀ = 0,5; Oj = 1 не отвергается при уровне значимости а = 0.05.

Б) Критерий Смирнова

Вычисляем значение статистики Смирнова по формуле

Sm = (6*n*Dn+1)²/9n

S_m =2,1964. Критическое значение статистики S_m при уровне значимости а = 0.05 равно 5,9915. Поскольку полученное по выборке значение статистики не превышает критического, гипотеза о согласии с нормальным распределением с параметрами 0₀ =0,5; В_} = 1 не отвергается при уровне значимости а = 0.05.

B) Критерий ω² Мизеса

Вычисляем значение статистики ω² Мизеса по формуле

Sω = nω²_n = 1/12n+∑(F(x_i,θ)-2i-1*2n)2

Sω =0,1148. Критическое значение статистики Sω при уровне значимости а = 0.05 равно 0,4614. Поскольку полученное по выборке значение статистики не превышает критического, гипотеза о согласии с нормальным распределением с параметрами 0₀ =0,5; Oj = 1 не отвергается при уровне значимости а = 0.05.

Г) Критерий Ω² Мизеса

Вычисляем значение статистики Ω² Мизеса по формуле

S_Ω = nΩ²_n = -n-2∑(2i-1/2n*ln(Fx_i,θ)+(1-2i-1/2n)ln(1 - Fx_i,θ))

S_Ω = 0,7577. Критическое значение статистики S_n при уровне значимости а = 0.05 равно 2,4924. Поскольку полученное по выборке значение статистики не превышает критического, гипотеза о согласии с нормальным распределением с параметрами 0₀ =0,5; Q_l = 1 не отвергается при уровне значимости а = 0.05.

Как видим, при задании уровня значимости нет оснований для отклонения проверяемой гипотезы по всем критериям согласия.

Список литературы

1.     Национальное счетоводство: Учебник / Под ред. Б. И. Башкатова. - 2-е издание. перераб. и доп. - М.: Финансы и статистика, 2002.

2.     Национальные счета в переходный период. - М.: Госкомстат России, 1994. – с. 63

3.     Экономическая статистика: Учебник. 2-е изд.. доп. / Под ред. Иванова Ю. Н. — М.: ИНФРА-М, 2002.

4.     Макроэкономическая статистика: Учеб. пособие / Салин В. Н., Медведев В Г. к др. -М. : Дело. 2001.

5.     Башкатов Б.И. Социально-экономическая статистика – М.: ЮНИТИ-ДАНА 2002. – 703 с.

6.     Боярский А.Я., Громыко Г.Л. “Общая теория статистики” М.: изд. Московские университеты, 1985 г. – 372 с.

7.     Васильева Э.К. “Социально-демографический портрет студента” М.: Мысль, 1986 г. – 96 с.

8.     Кильдишев и др. “Статистика населения с основами демографии” М.: Финансы и Статистика, 1990 г. – 312 с.