МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ ГОУ ВПО
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА СТАТИСТИКИ
Контрольная
работа по статистике
Вариант №12
Проверила: Божко Т.Н.
Выполнила:
ст. III
курса, Финансы и кредит, Банковское дело, второе высшее.
Воронеж
2008 г.
Задание 1
Имеются следующие выборочные данные
(выборка 25%-ная механическая), о доходах и расходов бюджетов субъектов РФ за
полугодие, млн. руб.
|
Доходы
|
расходы
|
|
4,2
|
4,9
|
|
3,8
|
4,7
|
|
6,4
|
7
|
|
4,4
|
5
|
|
4,7
|
4,2
|
|
2
|
1,9
|
|
4
|
4,7
|
|
3,7
|
4,3
|
|
7,1
|
6,8
|
|
4,2
|
4,6
|
|
2,6
|
3,1
|
|
4,5
|
4,8
|
|
5,5
|
7,1
|
|
5
|
5,5
|
|
1,5
|
1,8
|
|
1,6
|
1,7
|
|
3,4
|
3,6
|
|
4
|
4,5
|
|
3,5
|
3,6
|
|
2,3
|
2
|
|
3,5
|
3,9
|
|
4,4
|
5,8
|
|
4,8
|
4,4
|
|
7,5
|
8,7
|
|
4,6
|
4,6
|
|
3,1
|
3,3
|
|
4
|
4,6
|
|
5,2
|
6
|
|
5,3
|
5,8
|
|
5,2
|
5,1
|
Признак
– доходы бюджета.
Число
групп – пять.
Решение
1)
Для
построения группировки субъектов по уровню доходов с выделением 5 групп найдем
величину равного интервала:
Величина
равного интервала определяется по формуле:
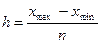 ,
,
где
xmax
и xmin –
максимальное и минимальное значение признака,
n – число
групп.
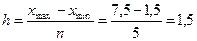
где
xmax=7,5, xmin=1,5 - максимальное
и минимальное значение.
n=5 – группы предприятий.
Путем
прибавления величины интервала к минимальному значению признака в группе
получим следующие группы субъектов РФ по уровню доходов (табл. 2.1).
Таблица
2.1
|
Ряд распределения
|
|
№ группы
|
Группы
субъектов
|
Число субъектов
|
Удельный вес
|
|
|
x
|
f
|
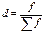
|
|
1
|
1,5-2,7
|
5
|
0,2
|
|
2
|
2,7-3,9
|
6
|
0,2
|
|
3
|
3,9-5,1
|
12
|
0,4
|
|
4
|
5,1-6,3
|
4
|
0,1
|
|
5
|
6,3-7,5
|
3
|
0,1
|
|
Всего
|
30
|
1
|
2) Для расчета характеристик интервального ряда построим вспомогательную
таблицу 2.2.
Таблица 2.2
|
№
|
Xi-Xi-1
|
f
|
Середина интервала
X
|
Xf
|
(x-x)2f
|
|
1
|
1,5-2,7
|
5
|
2,1
|
10,5
|
23,328
|
|
2
|
2,7-3,9
|
6
|
3,3
|
19,8
|
5,5296
|
|
3
|
3,9-5,1
|
12
|
4,5
|
54
|
0,6912
|
|
4
|
5,1-6,3
|
4
|
5,7
|
22,8
|
8,2944
|
|
5
|
6,3-7,5
|
3
|
6,9
|
20,7
|
20,9088
|
|
Итого
|
30
|
|
127,8
|
58,752
|
Средний доход бюджетов субъектов
(средняя арифметическая взвешенная) определяется по формуле:
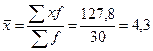 (млн. руб.)
(млн. руб.)
Среднее
квадратическое взвешенное отклонение по формуле:

В среднем, отклонение от среднего
бюджета составляет 1,4 млн. руб.
Коэффициент вариации определяется по формуле:
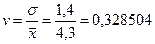 или 32,85%
или 32,85%
В среднем, отклонение от
среднего бюджета составляет 32,85%. Так как коэффициент вариации менее 33%,
следовательно, совокупность однородна.
Моду
определяем по формуле:
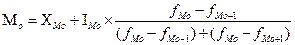 = =
= =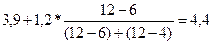 (млн. руб.)
(млн. руб.)
Мода равна 4,4 млн. руб.
Медиану определяем по формуле:
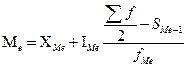 =
= 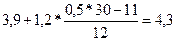 (млн. руб.)
(млн. руб.)
Из
расчета видно, что половина бюджетов до 4,3 млн. руб., а половина – больше
этого значения.
Задание 2
Установите наличие и
характер связи между признаками – доходы
и расходы, образовав пять групп с равными интервалами по обоим
признакам, методом аналитической группировки.
Решение
1)
Для построения группировки субъектов по доходам с выделением 5 групп
воспользуемся расчетами, полученными из первого задания.
Используя
полученные числа, получим следующие группы субъектов федерации (табл. 2.3).
Таблица 2.3
|
№ группы
|
Группировка
|
Доходы
|
Расходы
|
|
1
|
1,5-2,7
|
1,5
|
1,8
|
|
1,6
|
1,7
|
|
2
|
1,9
|
|
2,3
|
2
|
|
2,6
|
3,1
|
|
Итого
|
10,0
|
10,5
|
|
2
|
2,7-3,9
|
3,1
|
3,3
|
|
3,4
|
3,6
|
|
3,5
|
3,6
|
|
3,5
|
3,9
|
|
3,7
|
4,3
|
|
3,8
|
4,7
|
|
Итого
|
21,0
|
23,4
|
|
3
|
3,9-5,1
|
4
|
4,7
|
|
4
|
4,5
|
|
4
|
4,6
|
|
4,2
|
4,9
|
|
4,2
|
4,6
|
|
4,4
|
5
|
|
4,4
|
5,8
|
|
4,5
|
4,8
|
|
4,6
|
4,6
|
|
4,7
|
4,2
|
|
4,8
|
4,4
|
|
5
|
5,5
|
|
Итого
|
52,8
|
57,6
|
|
4
|
5,1-6,3
|
5,2
|
6
|
|
5,2
|
5,1
|
|
5,3
|
5,8
|
|
5,5
|
7,1
|
|
Итого
|
21,2
|
24,0
|
|
5
|
6,3-7,5
|
6,4
|
7
|
|
7,1
|
6,8
|
|
7,5
|
8,7
|
|
Итого
|
21,0
|
22,5
|
Для установления наличия и характера связи по данным
рабочей таблицы 2.3 построим итоговую аналитическую таблицу 2.4.
Таблица 2.4
|
№
группы
|
Группировка
субъектов
|
Число
субъектов
|
Доходы
|
Расходы
|
|
Всего
|
В
среднем
|
Всего
|
В
среднем
|
|
1
|
1,5-2,7
|
5
|
10,0
|
2,0
|
10,5
|
2,1
|
|
2
|
2,7-3,9
|
6
|
21,0
|
3,5
|
23,4
|
3,9
|
|
3
|
3,9-5,1
|
12
|
52,8
|
4,4
|
57,6
|
4,8
|
|
4
|
5,1-6,3
|
4
|
21,2
|
5,3
|
24,0
|
6
|
|
5
|
6,3-7,5
|
3
|
21,0
|
7,0
|
22,5
|
7,5
|
Данные таблицы 2.4
показывают, что с ростом доходов растут
расходы. Следовательно, между исследуемыми признаками существует прямая корреляционная
зависимость.
2) С помощью закона
сложения дисперсий можно оценить удельный вес факторов, лежащих в основе
группировки, во всей совокупности факторов, воздействующих на результативный
признак. Для этого применяется коэффициент детерминации, который рассчитывается
как отношение факторной дисперсии к общей дисперсии результативного признака:
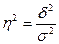
Рассчитаем групповые дисперсии по
формуле:
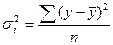
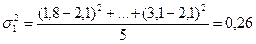
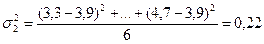
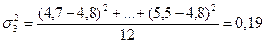
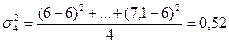
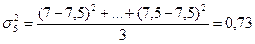
Рассчитаем среднюю из внутригрупповых
дисперсий по формуле:
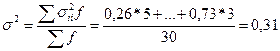
Рассчитаем
межгрупповую дисперсию по формуле:
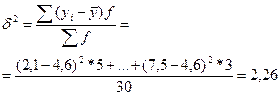
Рассчитаем общую дисперсию:
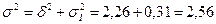
Рассчитаем
коэффициент детерминации:

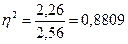
Данный коэффициент означает, что на 88,09%
вариация расходов обусловлено различиями в доходах и на 11,91% - влиянием
прочих факторов.
Эмпирическое корреляционное отношение
определяется по формуле:
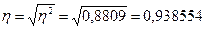
Так как полученное значение очень близко к
единице, следовательно, связь между расходами и доходами бюджетов тесная.
Задание 3
По результатам выполнения
1 с вероятностью 0,683 определите:
1. Ошибку выборки среднего дохода бюджета и границы, в которых
он будет находиться в генеральной
совокупности.
2. Ошибку выборки доли
регионов со средним доходом бюджета 5,1 млн. руб. и более и границы, в
которых будет находиться генеральная доля.
Решение
1) Определим
ошибку выборки среднего уровня:
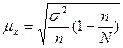
где dг - дисперсия выборки

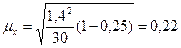
Предельная ошибка среднего уровня затрат определяется по формуле:
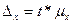
где t – коэффициент доверия (по таблице функции Лапласа находит такое значение аргумента,
для которого Ф(1)=0,683, следовательно t=1).
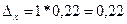
С вероятностью 0,683
можно утверждать, что средний доход в генеральной совокупности находится в
пределах 4,3±0,22 млн. руб. или от 4,08 млн. руб. до 4,52 млн. руб.
2) Проанализировав
исходные данные, видим, что в выборке количество субъектов с доходами 5,1 млн.
руб. и более равняется 7, поэтому долю найдем по формуле:
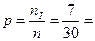 0,23 или 23%.
0,23 или 23%.
Определим ошибку выборки
доли:
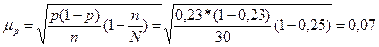
Предельная ошибка доли:
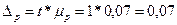 или 7%
или 7%
С вероятностью 0,683
можно утверждать, что доля субъектов с доходами 5,1 млн. руб. и более в
генеральной совокупности находится в пределах 23±7% или от 16% до 30%.
Задание 4
Налоговые поступления в региональный бюджет характеризуется
следующими данными, млрд. руб.:
Таблица 2.5
|
Месяц
|
Налоговые поступления
|
|
1-й
|
2-й
|
3-й
|
|
Январь
|
0,62
|
0,72
|
0,74
|
|
Февраль
|
0,65
|
0,75
|
0,77
|
|
Март
|
0,70
|
0,76
|
0,78
|
|
Апрель
|
0,72
|
0,77
|
0,82
|
|
Май
|
0,74
|
0,8
|
0,84
|
|
Июнь
|
0,76
|
0,82
|
0,85
|
|
Июль
|
0,71
|
0,78
|
0,8
|
|
Август
|
0,70
|
0,75
|
0,78
|
|
Сентябрь
|
0,82
|
0,88
|
0,9
|
|
Октябрь
|
0,85
|
0,89
|
0,96
|
|
Ноябрь
|
0,88
|
0,94
|
0,99
|
|
Декабрь
|
0,9
|
0,98
|
1,05
|
Для анализа сезонности налоговых поступлений в бюджет региона:
1. рассчитайте индексы сезонности методом простой средней.
2. постройте график
сезонности волны.
3. осуществите прогноз поступления налогов в бюджет региона, используя
индексы сезонности и исходя из того, что общий объем налоговых поступлений в
следующем (4-ом) году составит 11,4 млрд. руб.
Решение
1) Определение
индексы сезонности находим по формуле:
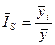 ∙100,
∙100,
где 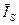 – индекс сезонности;
– индекс сезонности;
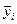 - средняя
величина уровня (за три года);
- средняя
величина уровня (за три года);
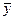 - среднемесячный уровень для всего ряда.
- среднемесячный уровень для всего ряда.
Для
расчета индекса сезонности построим дополнительную таблицу 2.6.
Таблица 2.6
|
Месяц
|
1
год
|
2
год
|
3
год
|
Среднемесячная
|
Индекс
сезонности
|
|
Январь
|
0,62
|
0,72
|
0,74
|
0,693333
|
85,57
|
|
Февраль
|
0,65
|
0,75
|
0,77
|
0,723333
|
89,27
|
|
Март
|
0,7
|
0,76
|
0,78
|
0,746667
|
92,15
|
|
Апрель
|
0,72
|
0,77
|
0,82
|
0,77
|
95,03
|
|
Май
|
0,74
|
0,8
|
0,84
|
0,793333
|
97,91
|
|
Июнь
|
0,76
|
0,82
|
0,85
|
0,81
|
99,97
|
|
Июль
|
0,71
|
0,78
|
0,8
|
0,763333
|
94,21
|
|
Август
|
0,7
|
0,75
|
0,78
|
0,743333
|
91,74
|
|
Сентябрь
|
0,82
|
0,88
|
0,9
|
0,866667
|
106,96
|
|
Октябрь
|
0,85
|
0,89
|
0,96
|
0,9
|
111,07
|
|
Ноябрь
|
0,88
|
0,94
|
0,99
|
0,936667
|
115,60
|
|
Декабрь
|
0,9
|
0,98
|
1,05
|
0,976667
|
120,53
|
|
Итого
|
9,05
|
9,84
|
10,28
|
|
|
|
В среднем
|
0,754167
|
0,82
|
0,856667
|
0,810278
|
|
Расчет индекса проводится
в следующем порядке:
а). Подсчитаем
среднемесячные налоговые поступления как
простое арифметическое среднее за три года. Например, yянварь = (0,62+0,72+0,74)/3=0,693333 и т.д.
б). После расчета
среднемесячных налоговых поступлений по
месяцам найдем среднемесячные поступления за три года как простое арифметическое
среднее.
yi = (yянварь + yфевраль + ….+ yноябрь +yдекабрь)/12 = (0,693333+ …+0,976667)/12 = 0,810278
в). Индекс сезонности
рассчитываем по формуле:
Is январь = 0,693333/0,810278*100 = 85,57%
Is февраль = 0,723333/0,810278*100=89,27% и т.д.
Результаты расчетов
индекса сезонности представлены в графе «Индекс сезонности» дополнительной
таблицы.
2). Построим график
сезонной волны.
Для
наглядного представления сезонной волны индексы сезонности изображают в виде
графика. Построение графика основывается на результатах предыдущего пункта с
использованием MS Excel XP. По оси Х откладываем месяца года, а по оси Y – величины индекса сезонности.
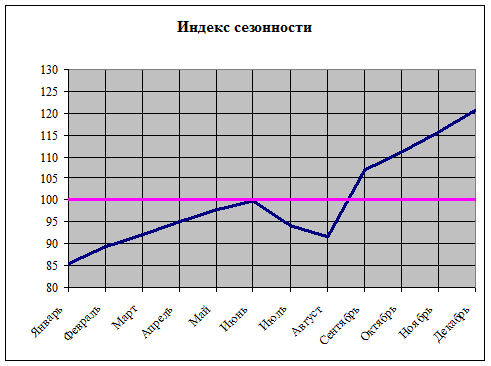
Рис. 1 Ряд
Индекс сезонности
3.
Исчислим прогноз поступления налогов в бюджет региона,
используя индексы сезонности и исходя из того, что общий объем налоговых поступлений
в следующем (4-ом) году составит 11,4 млрд. руб. Запланированные поступления
на 4-ый год составляет 11,4 млрд. руб. , в среднем в месяц – 0,95 млрд. руб.
(11,4/12 = 0,95), но с учетом индекса сезонности рассчитаем прогнозные поступления.
Yянварь = 0,95 * 85,57% = 0,81
Yфевраль = 0,95* 89,27% = 0,85 и т.д.
Результаты
объема налоговых поступлений по месяцам представлены в выходной таблице 2.7.
Таблица 2.7
Объемы поступлений на 4-ый год
(прогноз)
|
Месяц
|
Индекс, %
|
Поступления налогов в 4-ом году,
млрд. руб.
|
|
Январь
|
85,57
|
0,81
|
|
Февраль
|
89,27
|
0,85
|
|
Март
|
92,15
|
0,88
|
|
Апрель
|
95,03
|
0,90
|
|
Май
|
97,91
|
0,93
|
|
Июнь
|
99,97
|
0,95
|
|
Июль
|
94,21
|
0,89
|
|
Август
|
91,74
|
0,87
|
|
Сентябрь
|
106,96
|
1,02
|
|
Октябрь
|
111,07
|
1,06
|
|
Ноябрь
|
115,60
|
1,10
|
|
Декабрь
|
120,53
|
1,15
|