Задача 1.

За 2001 год выявлено всего 9587 человек, совершивших кражи, в том числе: в возрасте 14-15 лет – 268 чел; 16-17 лет – 1717 чел; 18-24 года – 3854 чел; 25-29 лет – 2381 чел; 30-49 лет – 1203 чел; 50 лет и старше – 164 чел.

Постройте график вариационного ряда возрастного распределения лиц, совершивших преступления, охарактеризуйте возрастную структуру, вычислите средний возраст лиц, совершивших преступления.

Решение. В каждой возрастной группе выберем средний возраст и припишем ему число совершённых краж по данной группе. Когда говорят о возрасте, то имеют в виду число полных лет. Так что в первой группе 14-15 лет учитывается возраст от 14 до 16 лет (не доходя до 16) и средний возраст будет 15 лет. В третьей группе середина придётся на 21, 5 лет (с математической точки зрения).

В последней возрастной группе средний возраст пусть будет 70 лет, этим самым мы учтём возраст от 50 лет до 70 лет. Получается вариационный ряд.

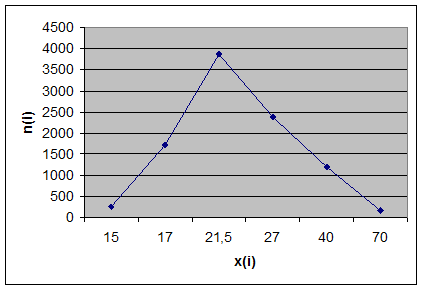
График вариационного ряда указывает на особую восприимчивость к воровству 2, 3 и 4 возрастных групп. Средний возраст таких преступников выпадает, скорее всего, на 3 возрастную группу. Проведём точные математические вычисления.

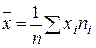= 1 / 9587∙ (15 ∙ 268 + 17 ∙ 1 717 + 21,5 ∙ 3854 + 27 ∙ 2381 + 40 ∙ 1203 + 70 ∙ 164) = 24,65

Полных лет получается для среднего возраста 24.

Задача 2.

По следующим данным о зарегистрированных случаях изнасилований определите среднее, модальное и медианное число обвиняемых по одному уголовному делу:

Решение.  

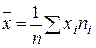= 1 / 773 ∙ ( 1 ∙ 458 + 2 ∙ 134 + 3 ∙ 126 + 4 ∙ 40 + 5 ∙ 15) = 1,7

Модальное число Мо = 1, для него самое большое число уголовных дел.

Медианное число Ме = 3, оно ровно по середине для числа обвиняемых n = 1, 2, 3, 4, 5.

Задача 3.

Выясните, какой из представленных показателей отличается большей вариативностью значений в рассматриваемый период:

Решение. Для каждого вида преступлений вычисляем размах вариации

R = x_max – x_min ,

среднелинейное отклонение

,

дисперсию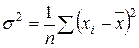

и среднеквадратическое отклонение σ.

При этом нам понадобятся средние величины

, .

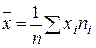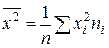Тогда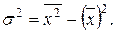

Сначала рассматриваем первый показатель

Х_max = 2945; Х_min = 2398.

R = 547.

? = 1 / 6 ∙ (2650 + 2814 + 2945 + 2398 +2719 + 2790) = 2719

Теперь L = 1 / 6 ∙ (69 + 95 + 226 + 321 + 71) = 130,3

Далее,

Более точный результат будет, если будем работать с меньшими числами.

В нашем случае проще вычислить σ²   по формуле:

   = 1 / 6 ∙ ( 69² + 95² + 226² + 0² + 71²) = 1 / 6 ∙ (4761 + 9025 +51076 + 103041 + 5041) = 28824; σ = 170.

Теперь рассматриваем второй показатель

X_max = 1211; X_min = 987; R = 224.

? = 1 / 6 ∙ (1018 + 987 + 1016 + 1123 +1190 +1211) = 1091

L = 1 / 6 ∙ (73 + 104 + 75 + 32 + 99 + 120) = 83,8

? = 1 / 6 ∙ (5329 + 10816 +5625 + 1024 +9801 + 14400) = 7832,5; σ = 88,5.

Полученные данные сведём в одну таблицу.

По всем показателям большей вариативностью значений в период с 1996 года по 2001 год обладает число зарегистрированных преступлений в состоянии алкогольного опьянения.

Задача 4.

Охарактеризуйте динамику числа зарегистрированных умышленных убийств стране за период 1995-2001 годы, рассчитав базисные, цепные и средние показатели: абсолютного прироста, темпа роста, темпа прироста, цепные показатели абсолютного значения 1% прироста. Определите ожидаемое число умышленных убийств в 2002 году на основе уравнения тренда, построенного по линейной функции методом аналитического выравнивания. Постройте график фактической динамики зарегистрированного числа убийств и полученной линии тренда.

Решение. Базисная форма расчёта показателей. Вычисления простые и сразу можно заполнять таблицу.

Теперь рассматривается цепная форма расчёта показателей.

Теперь переходим к аналитическому выравниванию ряда динамики по формуле y(t) = a₁ t + a₀.

 Сначала надо договориться относительно времени t. Расчётные формулы принимают простой вид, если

Это получится, если взять

T = 1998 – T.

   = 2932,

  = - 8760 – 6044 – 3077 + 2885 + 5960 + 8070 = - 966;

y (t) = 2932 -34,5t

  = 2794 – ожидаемое число умышленных убийств на 2002 год.

Задача 5.

Для изучения общественного мнения о работе правоохранительных органов в порядке собственно-случайного повторного отбора было опрошено 230 человек, что составляет 1% от общей численности городского населения. Средний возраст одного опрошенного составил 34,8 года.

Определите уровень предельной ошибки среднего возраста по выборочному наблюдению, если известно следующее повозрастное распределение жителей города в целом:

Решение.

N = Σ n_i = 230 – объём выборки.

  = 38,1 – средний возраст по выборке.

   = 145,1.

   = 1 / 230 ∙ (5² ∙ 16 + 15² ∙ 25 + 25² ∙ 39 + 35² ∙ 45 + 45² ∙ 49 + 55² ∙ 28 + 65² ∙ 15 + 75² ∙ 8 + 85² ∙ 4 + 95² ∙ 1) = 1807,6;

   = 1662,5; σ = 40,8.

  = 40,8 / 15,2 = 2,69

    = 5,38 ≈ 5,4

   = 34,8 (по условию)

У нас получается

   = 38,1 + 5,4 = 43,5;

   = 38,1 – 5,4 = 32,7.

Теория вероятностей утверждает, что с вероятностью  95,4% должно быть:

32,7 <   < 43,5.

Поскольку   = 34,8, то у нас это получилось.

С вероятностью 68,3% ?  должно попасть в интервал (35,4; 40,8).

Вот это у нас не получается. Но и вероятность р = 0,683 далека от единицы.