Задача 1.
Оптимальный план размещения
рекламы.
Фирма
планирует рекламную кампанию нового продукта. Отведенный на эти цели бюджет
составляет 120 000 руб. Предполагается, что тираж рекламных объявлений должен
составить не менее 800 млн экземпляров; объявления будут размещены в шести
изданиях. Каждое издание имеет свой тираж (см.таблицу). Фирма подсчитала
стоимость размещения рекламы в одном выпуске издания.
|
№ издания
|
Стоимость
размещения рекламы в одном выпуске издания, руб.
|
Тираж одного
выпуска, млн экз.
|
|
1
|
1474,2
|
9,9
|
|
2
|
1244,1
|
8,4
|
|
3
|
1131
|
8,2
|
|
4
|
700,7
|
5,1
|
|
5
|
530
|
3,7
|
|
6
|
524,4
|
3,6
|
Необходимо распространить рекламу с минимальными издержками при
следующих ограничениях:
1) в каждом издании реклама
должна пройти в шести или более выпусках;
2) на любое издание может быть
истрачено не более одной трети отпущенной суммы;
3) общая стоимость рекламы в
третьем и четвёртом изданиях не должна превышать 75 000 руб.
Решение:
Экономико – математическая
модель задачи:
Введём следующие
обозначения:
i – номер издания ( i=1,…п; п=6)
хi - количество выпусков в издании i
Т – тираж рекламных объявлений ( Т=800 млн экз)
К – бюджет (К=120 000 руб)
сi – стоимость рекламы в
издании i
ti – тираж выпуска в издании I
Экономико-математическая модель задачи будет иметь вид:
f(X)
= 
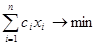
Ограничения:
; 
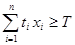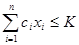; cixi
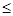1/3К; x i
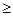6 i=1,…,п (п=6)
Подставляя исходные данные,
имеем:
1474,2х1+1244,1х2+1131х3+700,7х4+530х5+524,4х6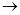
min
Ограничения:
9,9х1+8,4х2+8,2х3+5,1х4+3,7х5+3,6х6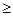 800 (млн экз)
1474,2х1+1244,1х2+1131х3+700,7х4+530х5+524,4х6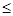120 000 (руб)
1131х3+700,7х4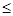75 000 (руб)
1474,2х1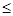40 000
1244,1х2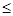40 000
1131х3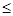40 000
700,7х4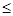40 000
530х5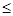40 000
524,4х6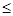40 000 хi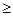6; i=1…п (п=6)
Решение задачи с помощью надстройки Поиск решения
в среде Excel:
В нашей задаче оптимальные
значения вектора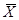 
=(х1,х2,х3,х4,х5,х6)
будут помещены в ячейках А2:F2,
оптимальное значение целевой функции – в ячейке G3. Также введём исходные данные задачи
(рис.1)
|
X1
|
X2
|
X3
|
X4
|
X5
|
X6
|
|
6
|
|
|
|
|
|
|
|
|
|
1474,2
|
1244,1
|
1131
|
700,7
|
530
|
524,4
|
|
|
|
9,9
|
8,4
|
8,2
|
5,1
|
3,7
|
3,6
|
|
800
|
|
1474,2
|
1244,1
|
1131
|
700,7
|
530
|
524,4
|
|
120000
|
|
|
1131
|
700,7
|
|
|
|
75000
|
|
1474,2
|
|
|
|
|
|
|
40000
|
|
1244,1
|
|
|
|
|
|
40000
|
|
|
1131
|
|
|
|
|
40000
|
|
|
|
700,7
|
|
|
|
40000
|
|
|
|
|
530
|
|
|
40000
|
|
|
|
|
|
524,4
|
|
40000
|
Рис.1. Введены
исходные данные.
Затем вводим зависимость для целевой функции, используя кнопку Мастер
функций, расположенной
на панели инструментов. В окне Категория выбираем категорию Математические, в окне Функции выбираем строку СУММПРОИЗВ. В строку Массив 1 вводим А2:F2, в
строку Массив 2 вводим
А3:F3. Массив 1 будет использоваться при вводе зависимостей для
ограничений, поэтому на этот массив делаем абсолютную ссылку ($A$2:$F$2).
Ноль в ячейке G3 показывает, что в эту ячейку введена функция. С
помощью кнопки Копировать и Вставить на панели инструментов,
вводим зависимости для всех ограничений. (рис.2)
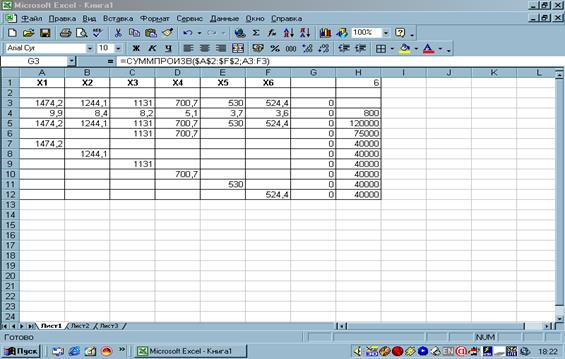
Рис.2. Введены
зависимости для всех ограничений.
После этого нужно запустить команду Поиск решения (в строке Меню,
Сервис). Устанавливаем
целевую ячейку, вводим адрес ячейки $G$3. Вводим тип целевой
функции, в данном случае целевая функция равна Минимальному значению. В строке Изменяя
ячейки вводим адреса
искомых переменных A$2:F$2. Затем вводим ограничения
с помощью кнопки Добавить. После введения всех ограничений нажимаем кнопку ОК. С помощью кнопки Параметры
устанавливаем флажки в
окнах Линейная модель (это обеспечит применение симплекс-метода) и Неотрицательные
значения. Нажимаем ОК.
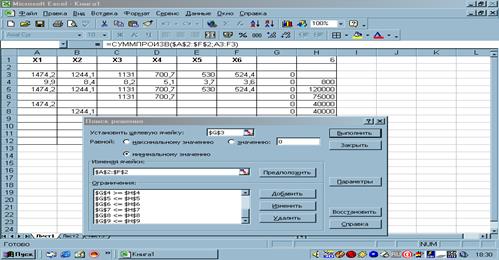
Рис.3. Введены
все условия задачи.
После этого в диалоговом окне Поиск решения нажимаем кнопку Выполнить.
Через непродолжительное время появятся результаты Поиска
решения и исходная
таблица с заполненными ячейками A3:F3 для значений хi и ячейка G3 с минимальным значением
целевой функции.
|
X1
|
X2
|
X3
|
X4
|
X5
|
X6
|
|
6
|
|
6
|
6
|
30,94607
|
57,08577
|
33,43374
|
6
|
|
|
|
1474,2
|
1244,1
|
1131
|
700,7
|
530
|
524,4
|
112176,1
|
|
|
9,9
|
8,4
|
8,2
|
5,1
|
3,7
|
3,6
|
800
|
800
|
|
1474,2
|
1244,1
|
1131
|
700,7
|
530
|
524,4
|
112176,1
|
120000
|
|
|
1131
|
700,7
|
|
|
75000
|
75000
|
|
1474,2
|
|
|
|
|
|
8845,2
|
40000
|
|
1244,1
|
|
|
|
|
7464,6
|
40000
|
|
|
1131
|
|
|
|
35000
|
40000
|
|
|
|
700,7
|
|
|
40000
|
40000
|
|
|
|
|
530
|
|
17719,88
|
40000
|
|
|
|
|
|
524,4
|
3146,4
|
40000
|
Рис.4. Решение
получено.
В результате решения задачи был получен ответ: фирме необходимо
разместить рекламные объявления в первом издании – в шести выпусках, во втором
– в шести выпусках, в третьем – в тридцати одном выпуске, в четвёртом – в
пятидесяти семи выпусках, в пятом – в тридцати трёх выпусках и в шестом – в
шести выпусках.
Задача 2.
Транспортная задача.
Менеджер
транспортного отдела составляет план перевозок продукции фирмы в стандартных
контейнерах на следующий месяц. Цены перевозок одного контейнера, величины
заказов и запасы на складах даны в таблицах.
|
Склады
|
Клиенты
|
Ресурсы
|
|
К1
|
К2
|
К3
|
К4
|
К5
|
К6
|
К7
|
К8
|
К9
|
К10
|
|
С1
|
3
|
17
|
7
|
17
|
9
|
14
|
9
|
14
|
8
|
14
|
4
|
|
С2
|
3
|
6
|
6
|
8
|
17
|
12
|
16
|
5
|
5
|
13
|
11
|
|
С3
|
9
|
5
|
6
|
16
|
8
|
10
|
11
|
8
|
8
|
18
|
17
|
|
С4
|
12
|
16
|
6
|
16
|
14
|
3
|
5
|
14
|
11
|
17
|
20
|
|
Заказ
|
2
|
2
|
5
|
4
|
5
|
4
|
4
|
1
|
2
|
3
|
|
Имеется
10 заказов от 10 потребителей. Заказы в сумме меньше запаса на складах С1,…,
С4. Найдите план перевозок, минимизирующий транспортные издержки.
Решение:
Экономико –
математическая модель задачи:
Продукция сосредоточена у т поставщиков Аi в количестве аi (i=1…, т) контейнеров,
необходимо доставить п потребителям Вj в количестве bj (j=1…,п) контейнеров. Известна стоимость сij перевозки одного контейнера от
поставщика i к потребителю j.
Обозначим через хij количество контейнеров, запланированных к перевозке от
поставщика i к потребителю j. Так как от поставщика i к потребителю j запланировано перевезти xij контейнеров, то стоимость перевозки составит cijxij. Стоимость
всего плана выразится двойной суммой Z=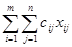
Систему ограничений получаем из
следующих условий задачи:
1) все контейнеры должны быть
перевезены, т.е.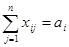 
, i=1,…,т
2) все потребности должны быть
удовлетворены, т.е.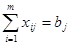 
, j=1,…, п
В нашей задаче суммарные запасы превышают суммарные потребности (задача
является открытой).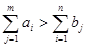 
. Линейная функция остаётся такой же, изменяется только вид
системы ограничений.
Z=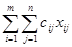
При
ограничениях:
,
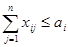i=1,…,т
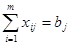, j=1,…,п. xij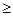0;
Открытая модель
решается приведением к закрытой модели, путём ввода фиктивного потребителя Вn+1, потребность которого
описывается формулой bn+1=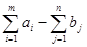
Стоимость перевозки единицы груза до фиктивного потребителя и стоимость
перевозки груза от фиктивного поставщика полагаются равными нулю, так как груз
в обоих случаях не перевозится.
Таким образом, математическая модель задачи имеет следующий вид:
Найти минимальное значение линейной
функции Z=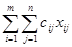
При ограничениях: ,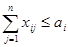
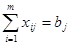, j=1,…,п. xij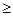0;
Решение транспортной задачи с помощью средства Excel Поиск решения:
Сначала создаём формы для решения задачи. Этот шаг предполагает
создание матрицы перевозок. Для этого необходимо выполнить
резервирование изменяемых ячеек, поэтому в блок ячеек В3:К6 вводятся «1» - так
резервируется место, где после решения задачи будет находиться распределение
поставок, обеспечивающих минимальные затраты на перевозку груза.
Затем вводим исходные данные. В конкретном примере осуществляется ввод
мощностей четырёх поставщиков (ячейки А10:А13), потребности клиентов (В9:К9), а
также затраты по доставке контейнеров от конкретного поставщика потребителю
(блок В10:К13).
|
1
|
|
|
|
|
|
|
|
|
|
|
|
Матрица
перевозок (изменяемые ячейки)
|
|
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
Исходные данные
|
|
|
2
|
2
|
5
|
4
|
5
|
4
|
4
|
1
|
2
|
3
|
|
4
|
3
|
17
|
7
|
17
|
9
|
14
|
9
|
14
|
8
|
14
|
|
11
|
3
|
6
|
6
|
8
|
17
|
12
|
16
|
5
|
5
|
13
|
|
17
|
9
|
5
|
6
|
16
|
8
|
10
|
11
|
8
|
8
|
18
|
|
20
|
12
|
16
|
6
|
16
|
14
|
3
|
5
|
14
|
11
|
17
|
Рис.5. Создание формы
для ввода условий задачи.
Ввод исходных данных и граничных условий.
Вводим условия реализации мощностей поставщиков, для этого, помещая
курсор в ячейку А3, выбираем знак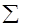 
, выделяем необходимые для суммирования ячейки В3:К3 и
нажимаем Enter для
подтверждения формулы. Аналогичные действия выполняем для ячеек А4, А5, А6.
Вводим условия удовлетворения запросов потребителей. Помещаем курсор в
ячейку В7, выбираем знак 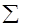, при этом автоматически выделяется весь столбец В3:В6,
нажимаем Enter для подтверждения
суммирования показателей выделенного столбца. Эту же последовательность
действий выполняем для ячеек С7:К7. Таким образом, введены ограничения для всех
поставщиков и потребителей.
Для вычисления значения целевой функции, соответствующей минимальным
суммарным затратам на доставку груза, необходимо зарезервировать ячейку. Для
этого необходимо поместить курсор в ячейку В15 (после решения задачи в данной
ячейке будет находиться значение целевой функции), запустить Мастер функций, в окне Категория
выбрать
Математические в окне Функция при помощи спинера выбрать
СУММПРОИЗВ нажать кнопку ОК, в окне СУММПРОИЗВ указать адреса
массивов, элементы которых обрабатываются этой функцией. В задаче целевая
функция представляет собой произведение затрат на доставку груза (расположенных
в блоке ячеек В10+К13) и объёмов поставок для каждого потребителя (содержимое
ячеек В3+К6)
В поле ячейки В15 появится некоторое числовое значение, равное
произведению единичных поставок на удельные коэффициенты затрат по доставке
грузов (в данной задаче - это число 416) (рис.6)
|
Матрица
перевозок (изменяемые ячейки)
|
|
10
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
10
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
10
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
10
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
4
|
4
|
4
|
4
|
4
|
4
|
4
|
4
|
4
|
4
|
|
Исходные данные
|
|
|
2
|
2
|
5
|
4
|
5
|
4
|
4
|
1
|
2
|
3
|
|
4
|
3
|
17
|
7
|
17
|
9
|
14
|
9
|
14
|
8
|
14
|
|
11
|
3
|
6
|
6
|
8
|
17
|
12
|
16
|
5
|
5
|
13
|
|
17
|
9
|
5
|
6
|
16
|
8
|
10
|
11
|
8
|
8
|
18
|
|
20
|
12
|
16
|
6
|
16
|
14
|
3
|
5
|
14
|
11
|
17
|
|
|
|
|
|
|
|
|
|
|
|
|
min
|
416
|
|
|
|
|
|
|
|
|
|
Рис.6. Введены
зависимости из математической модели.
Для ввода зависимостей из математической модели необходимо
выполнить следующие действия. Выбрать Сервис,
Поиск решения. Поместить курсор в Установить
целевую (ячейку), ввести адрес $B$15 (тем самым
мы резервируем ячейку, куда после решения задачи помещается значение целевой
функции). Установить направление изменения целевой функции, равное Минимальному значению. Ввести адреса изменяемых ячеек В3+К6.
Для этого необходимо выбрать Изменяя ячейки ввести адреса $B$3:$K$6.
В матрицу перевозок, содержащую исходные данные по задаче, необходимо
ввести условие реализации мощностей всех поставщиков. Для этого необходимо
выбрать Добавить ограничения, в поле Ссылка на ячейку ввести адреса $A$3:$A$6, в среднем поле установить
зна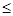к «», так как задача является открытой. В поле ограничения
установить адреса $A$10:$A$13, для подтверждения введенного условия нажать кнопку ОК.
Далее вводится ограничение, которое реализует условие удовлетворения
мощностей всех потребителей. Для этого необходимо выбрать Добавить ограничения, в поле Ссылка
на ячейку ввести адреса $B$7:$K$7. В поле знака выбрать при помощи спинера знак «=», в
поле Ограничение установить
адреса $B$9:$K$9, нажать кнопку ОК. После этого
надо вернуться в поле Поиск решения . После ввода
всех ограничений ввести ОК. На экране
появится окно Поиск решения с введенными
ограничениями.
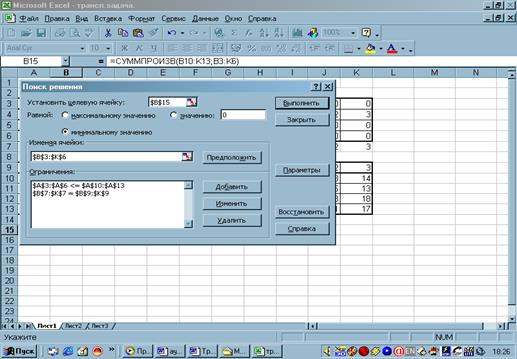
Рис.7. Ввод
зависимостей из математической модели.
С помощью окна Параметры можно вводить
условия для решения оптимизационных задач. В нашей задаче следует установить
флажок Неотрицательные значения и флажок Линейная модель, нажать кнопку ОК, после этого произойдёт переход в поле Поиск решения, нажать кнопку Выполнить.
На экране появится диалоговое окно Результаты
поиска решения. В результате нами был получен оптимальный план перевозок.
(рис.8)
|
|
|
|
|
|
|
|
|
|
|
|
Матрица
перевозок (изменяемые ячейки)
|
|
2
|
2
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
10
|
0
|
0
|
0
|
4
|
0
|
0
|
0
|
1
|
2
|
3
|
|
12
|
0
|
2
|
5
|
0
|
5
|
0
|
0
|
0
|
0
|
0
|
|
8
|
0
|
0
|
0
|
0
|
0
|
4
|
4
|
0
|
0
|
0
|
|
2
|
2
|
5
|
4
|
5
|
4
|
4
|
1
|
2
|
3
|
|
Исходные данные
|
|
|
2
|
2
|
5
|
4
|
5
|
4
|
4
|
1
|
2
|
3
|
|
4
|
3
|
17
|
7
|
17
|
9
|
14
|
9
|
14
|
8
|
14
|
|
11
|
3
|
6
|
6
|
8
|
17
|
12
|
16
|
5
|
5
|
13
|
|
17
|
9
|
5
|
6
|
16
|
8
|
10
|
11
|
8
|
8
|
18
|
|
20
|
12
|
16
|
6
|
16
|
14
|
3
|
5
|
14
|
11
|
17
|
|
|
|
|
|
|
|
|
|
|
|
|
min
|
204
|
|
|
|
|
|
|
|
|
|
Рис.8. Результаты
поиска решения.