ВАРИАНТ 1

ВАРИАНТ 1

Задача 1

УСЛОВИЕ ЗАДАЧИ

Сформируйте массив случайных чисел и произведите 30 – ную простую случайную бесповторную выборку.

По выборочным данным:

1) Постройте интервальный ряд распределения, образовав пять групп с равными интервалами.

2) Исчислите средний объем выпуска товаров и услуг, приходящийся на одно предприятие, а также долю предприятий с объемом выпуска товаров и услуг более 40 млн. рублей.

3) С вероятностью 0,954 определите доверительные интервалы, в которых можно ожидать генеральные параметры:

а) средний размер выпуска товаров и услуг одного предприятия

б) долю малых предприятий с объемом выпуска товаров и услуг более 40 млн. рублей.

в) общий объем выпуска товаров и услуг малыми предприятиями региона

г) число предприятий с объемом выпуска товаров и услуг более 40 млн. рублей.

РЕШЕНИЕ

1) Результаты простой случайной бесповторной выборки: 40;7;5;3;22;19;26;10;45;32;8;20;12;11;9;1;5;29;24;10;6;41;35;29;36

Величина интервала:

i = (х_мах-х_мин)/n = (45-1) / 5 = 8

Интервальный ряд распределения имеет вид, представленный в таблице 1.

Таблица 1

Интервальный ряд распределения

Границы интервала	Число попаданий в интервал, n	Средне значение внутри интервала, х	х*n
1--9	8	4,5	36
10--18	4	14,5	58
19--27	5	23,5	117,5
28--36	5	32,5	162,5
37--45	3	41,5	124,5
ИТОГО	25		498,5

2) средний объем выпуска товаров и услуг, приходящийся на одно предприятие:

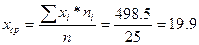
Количество предприятий с объемом выпуска более 40 млн. рублей – 3 штуки. Доля таких предприятий: 3/25 = 0,12 или 12 %.

3) При вероятности 0,954 и объеме выборки 25, найдем значение q в зависимости от верояности и объема выборки:

q = 0.32

Найдем доверительные интервалы:

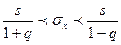
По среднему размеру выпуска найдем значение выборочной дисперсии:

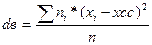
Таблица 2

ni	xi	(xi-x ср)	(xi-x ср)²	ni * (xi-x ср)²
8	4,5	-15,4	237,16	1897,28
4	14,5	-5,4	29,16	116,64
5	23,5	3,6	12,96	64,8
5	32,5	12,6	158,76	793,8
3	41,5	21,6	466,56	1399,68
ИТОГО				4272,2

dв = 4272,2/25 = 170,89

Выборочная дисперсия:

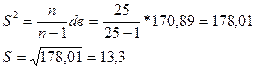
Тогда, доверительные интервалы равны:

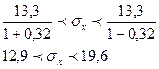
Таким образом, заданное средне значение попадает в доверительный интервал с нижней границей 12,9 и верхней границей – 19,6

Задача 2

УСЛОВИЕ ЗАДАЧИ

На основе 5 – процентной пропорциональной расслоенной (типической ) выборки со случайным отбором единиц в слое получены сведения о вкладах населения района области.

Результаты выборочного наблюдения обобщены в таблице 3.

Таблица 3

Типы населения	Число вкладов, тыс. ед.	Средний размер вклада, тыс. руб.	Коэффициент вариации, %
Городское	30	7	15
Сельское	20	5	21

Определите:

1) тесноту связи между типом населения и средним размером вклада, исчислив эмпирическое корреляционное отношение;

2) с вероятностью 0,954 доверительные интервалы, в которых можно ожидать:

а) средний размер вклада населения района области

б) общую сумму вкладов населения района

3) как изменится точность средней и предельной ошибок выборки, если предположить, что приведенные данные получены в результате простой случайной бесповторной выборки

РЕШЕНИЕ

1) Выборочный эмпирический корреляционный момент:

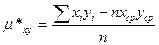
Пусть х - средний размер вклада, тыс. руб.

у - число вкладов, тыс. ед.

хср = (7+5)/ 2 = 6

у ср = (30+20)/2 = 25

Таблица 4

xi	yi	xi*yi	x*x	y*y
7	30	210	49	900
5	20	100	25	400
ИТОГО		310	74	1300

Тогда,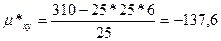

Выборочный корреляционный коэффициент:

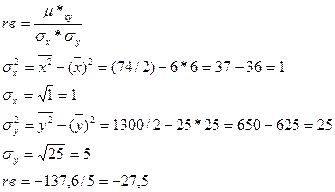
Таким образом, коэффициент корреляции показывает, что связь между типом населения и средним размером вклада нетесная

2) При вероятности 0,954 и объеме выборки 2 значение q равно 0,92

Найдем доверительные интервалы:

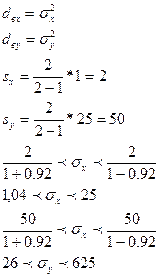
3) Если предположить, что приведенные данные получены в результате случайной бесповторной выборки, то точность ошибок увеличится.

Задание 3

По субъекту Российской Федерации имеются следующие данные

Таблица 5

Исходные данные

Показатель	2002 год	2002 год в % к 2000 году
Экспорт, млн. долл., всего	2708,5
в том числе
в страны вне СНГ	2306,3	120,3
в страны СНГ	402,2	80,3
Импорт, млн. долл.- всего	1077,4
в том числе
из стран вне СНГ	529,4	103,3
из стран СНГ	548	102,6

Определите:

1) недостающие элементы таблицы

2) географическую структуру экспорта и импорта в 2002 и 2002 годах

РЕШЕНИЕ

1) Составим пропорцию:

2306,3-120,3 %

х – 100 %

Отсюда, х = 2306,3*100/120,3 = 1917,1 (млн. долл.) – экспорт вне СНГ в 2000 году

Вторая пропорция:

402,2-80,3 %

х – 100 %

Отсюда, х = 402,2*100/80,3 = 500,9 (млн. долл.) - экспорт в СНГ в 2000 году

ПО импорту:

529,4-103,3 %

х – 100%

Отсюда, х = 529,4*100/103,3 = 512,5 (млн. долл.) – импорт в 2002 году с страны СНГ

Вторая пропорция:

548-102,6 %

х – 100 %

х = 534,1 (млн. долл.) – в 2000 году импорт из стран СНГ

Общий экспорт в 200 0 году : 500,9+1917,1 = 2418 млн. долл.

Общий импорт в 2000 году: 534,1+512,5 = 1046,61 (млн. долл.)

2002 год в % к 2000 году:

по экспорту: 2708,5*100/2418 = 112 (%)

по импорту: 1077,4*100/1046,6 = 102,9 (%)

Таблица 6

Показатель	2000 год	2002 год	Темп изменения, %
млн. дол.	структура, %	млн. долл.	структура, %
Экспорт, млн. долл., всего	2418	100	2708,5	100	112,01
в том числе
в страны вне СНГ	1917,1	79,28	2306,3	85,15	120,30
в страны СНГ	500,9	20,72	402,2	14,85	80,30
Импорт, млн. долл.- всего	1046,61	100,00	1077,4	100,00	102,94
в том числе
из стран вне СНГ	512,5	48,97	529,4	49,14	103,30
из стран СНГ	534,1	51,03	548	50,86	102,60

2) Географическая структура экспорта и импорта представлена на рисунках 1-4.

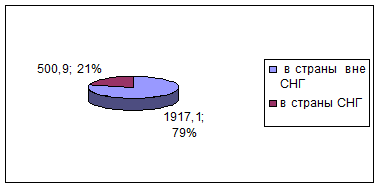
Рис. 1. Географическая структура экспорта в 2002 году

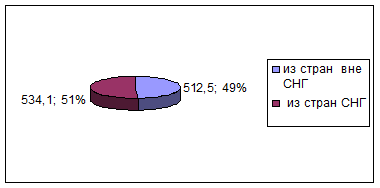
Рис. 2. Географическая структура импорта в 2002 году

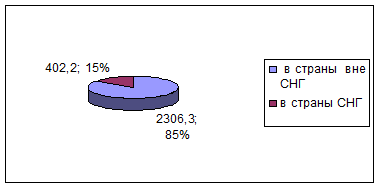
Рис. 3. Географическая структура экспорта в 2002 году

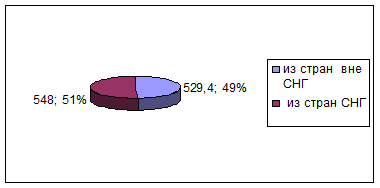
Рис. 4. Географическая структура импорта в 2002 году

Задача 4

УСЛОВИЕ ЗАДАЧИ

Имеются данные об экспорте филе рыбного

Таблица 6

Показатель	Базисный период	Отчетный период
количество, т	Стоимость. Тыс. долл.	количество, т	Стоимость. Тыс. долл.
Экспорт- всего	497	1483	491	1567
в том числе в страны
А	18	77	53	265
Б	262	907	410	1186
В	178	419	8	30
Г	-	-	20	86
Д	39	80	-	-

Определите:

1) По группе сопоставимых стран импортеров:

1.1. для оценки структурных изменений, произошедших в географическом распределении товаропотока, интегральный коэффициент структурных сдвигов К. Гатева

1.2. динамику средней цены 1 т поставленного на экспорт филе рыбного

1.3. в какой мере эта динамик обусловлена: изменением цены 1 т филе рыбного в каждую из стран, изменением квот на экспорт филе рыбного в страны

2) По всем странам импортерам:

2.1. Динамику средней цен 1 т поставленного на экспорт филе рыбного

РЕШЕНИЕ

1) ПО сопоставимым странам экспортерам

Таблица 7

Показатель	Базисный период	Отчетный период	Изменение цены 1 т, тыс. долл.
количество, т	стоимость, тыс. дол.	цена 1 т, тыс. долл.	количество, т	стоимость, тыс. дол.	цена 1 т, тыс. долл.
	у0		х0	у1		х1
А	18	77	4,28	53	265	5,00	0,72
Б	262	907	3,46	410	1186	2,89	-0,57
В	178	419	2,35	8	30	3,75	1,40

Средняя цена 1 т:

- базовый период: 10,09/3 =3,36 (тыс. долл.)

- отчетный период: 11,64/3 =3,88 (тыс. долл.)

Динамика средней цены:

3,88-3,36 = 0,52 (тыс. долл.)

Значит, цена в отчетном году выросла на 0,52 тыс. долл.

Динамика изменения средней цены 1 тонны филе рыбного обусловлена

1. изменением цены 1 т :

1,55/3 = 0,51

2. Изменением квот:

0,52-0,51 = 0,01

То есть в большей степени динамика изменения средней цены обусловлена изменением цены 1 т рыбного филе.

Определяем индекс структурных сдвигов.

Пусть х – цена за 1 тонну рыбного филе, тыс. долл.

у – объем экспорта, т.

Таблица 8

Вспомогательная таблица при определении индекса структурных сдвигов

	у0	х0	у1	х1	х1*у1	х0*у0
А	18	4,28	53	5,00	265	77
Б	262	3,46	410	2,89	1186	907
В	178	2,35	8	3,75	30	419
ИТОГО	458	10,09354	471	11,64268	1481	1403

Индекс структурных сдвигов:

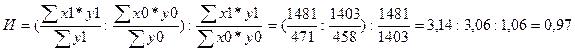
По всем странам

Таблица 9

Динамика цен по всем странам

Показатель	Базисный период	Отчетный период	Изменение цены 1 т, тыс. долл.
количество, т	стоимость, тыс. дол.	цена 1 т, тыс. долл.	количество, т	стоимость, тыс. дол.	цена 1 т, тыс. долл.
А	18	77	4,28	53	265	5,00	0,72
Б	262	907	3,46	410	1186	2,89	-0,57
В	178	419	2,35	8	30	3,75	1,40
Г	0	0	0,00	20	86	4,30	4,30
Д	39	80	2,05	0	0	0,00	-2,05
ИТОГО			12,14			15,94

Средняя цена :

- базовый период: 12,14/4 = 3,04 (тыс. долл.)

- отчетный период: 15,9/4 = 3,98 (тыс. дол.)

Динамика средней цены: 3,98-3,04 = 0,94 (тыс. дол.)

В целом по всем странам средняя цена выросла на 0,94 тыс. долл.

Задача 5

УСЛОВИЕ ЗАДАЧИ

Имеются следующие данные о продаже сельскохозяйственной продукции в январе отчетного года на городском рынке региона

Таблица 10

Виды продуктов	Продано	Средние цены
тонн	в % к январю базисного года	долл. за кг	в % к январю базисного года
А	3,3	87	5,32	106
Б	0,4	88	4,84	104
В	2,1	113	4,07	96

Определите:

1. Средний арифметический индекс физического объема оборота розничной торговли, общие индексы Ласпейраса и Г. Пааше, а также их аналоги в средней гармонической и арифметической форме, общий индекс оборотов розничной торговли

2. Общее изменение оборота розничной торговли всего и в том числе: за счет физического объема продажи товаров, цен на товары

РЕШЕНИЕ

1. Объем оборота определяется как произведение цен на количество проданных товаров

Таблица 11

Виды продукции	Базовый период	Отчетный период
цена	объем продаж, кг	объем продаж, долл.	цена	объем продаж, кг	объем продаж, долл.
	р0	q0	p0*q0	p1	Q1	p1*q1	p0*q1	p1*q0
А	5,02	3793,10	19037,09	5,32	3300,00	17556,00	16562,26	20179,31
Б	4,65	454,55	2115,38	4,84	400,00	1936,00	1861,54	2200,00
В	4,24	1858,41	7878,87	4,07	2100,00	8547,00	8903,13	7563,72
ИТОГО	13,91	6106,06	29031,34	14,23	5800,00	28039,00	27326,93	29943,03

Индекс физического оборота:

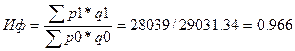
Индекс Ласпейраса:

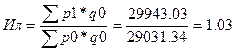
Индекс Пааше:

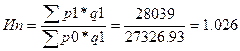
2. Общее изменение оборота розничной торговли:

28039-29031,34 = - 992,34 (долл.)

В целом оборот розничной торговли упал на 992,34 долл.

Определим влияние факторов:

1) изменение средней цены на товары:

Средняя цена на товары:

Базовый период: p0= 13,91/3 = 4,6

Отчетный период: p1 =14,23/3 = 4,7

V0 = q0*p0 = 6106,06*4,6 = 28087,9 (долл.)

V' = q0*p1 = 6106.06*4.7 = 28698.5 (долл.)

Влияние изменения средней цены:

28698,5-28087,9 = 610,6 (долл.)

2) изменение объема продаж в физической форме:

V’’= p1*q1=4.7*5800 = 27260 (долл.)

Влияние изменения объема продаж:

27260-28698,5 = -1438,5 (долл.)

Задача 6

УСЛОВИЕ ЗАДАЧИ

Численность населения города на конец года составила 700 тыс. чел. Известно, что в течение года в городе родилось 10, а умерло 12 тыс. чел., в том числе детей в возрасте до 1 ода – 200 человек. В анализируемом году выявлено положительное сальдо миграции, равное 12 тыс. чел.

Удельный вес женщин в возрасте 15-49 лет в общей среднегодовой численности населения города составил 30 %.

Определите:

1) численность населения города на начало года

2) среднегодовую численность населения города

3) общий и специальный коэффициенты рождаемости

4) общий коэффициент смертности

5) коэффициенты естественного прироста и миграции населения

6) коэффициенты жизненности, оборота и экономического воспроизводства населения

РЕШЕНИЕ

1) Численность населения на начало года:

700-10+12-12 = 690 (тыс. чел.)

2) Среднегодовая численность населения:

(700+690)/2 = 695 (тыс. чел.)

3) Коэффициент рождаемости:

10/700 = 0,014

4) Коэффициент смертности общий:

12/700 = 0,017

5) Коэффициент смертности детей

0,2/700 = 0,00029

6) Коэффициент естественного прироста:

(10+12)/700 = 0,03

7)Коэффициент миграции населения:

12/700 = 0,017

Задача 7

УСЛОВИЕ ЗАДАЧИ

По одной из организаций региона за отчетный период имеются данные:

1. Организация зарегистрирована и действует с 20 октября. Численность работников списочного состава в октябре составляла:

- 20 октября (понедельник) – 315 человек,

- 21 октября (вторник) – 305 человек

- 22 октября (среда) – 317 человек,

- 23 октября (четверг) – 320 человек,

- 24 октября (пятница) – 335 человек

- 25 и 26 октября – выходные дни

- 27 октября - 334 человека

- 28 октября – 330 человек

- 29 октября – 325 человек

- 30 октября – 310 человек

- 31 октября – 307 человек

Известно, что численность совместителей с 20 по 27 октября составила 70 человек, с 28 по 31 октября – 85 человек, а число работающих по договорам гражданско-правового характера зарегистрировано с 20 по 23 октября – 15 человек, а с 28 по 31 октября – 10 человек

В ноябре число явок на работу зарегистрировано 5859 человек – дней, число неявок по всем причинам – 3891 человеко – дней.

Среднесписочная численность ее работников за декабрь составила 320 человек.

Определите:

1. за октябрь: среднюю численность внешних совместителей, среднюю численность работников, выполнявших работу по договорам гражданско - правового характера

2. среднесписочную численность работников организации за год

РЕШЕНИЕ

1) средняя численность совместителей за октябрь: (70+75)/2 = 73 (человека)

2) средняя численность работников, работающих по договорам гражданско- правового характера: (15+10)/2 = 13 (человек)

3) среднесписочная численность работников за октябрь:

(315+305+317+320+335+334+330+325+310+307)/10 = 320 (человек)

3) среднесписочная численность в ноябре:

(5859-3891) /7 = 281 (чел.)

4) среднегодовая численность:

(320+281+320)/3 = 307 (человек)

Задача 8

УСЛОВИЕ ЗАДАЧИ

По субъекту Российской Федерации имеются следующие данные

Таблица 12

Исходные данные задачи

Млрд. руб.

Показатель	Значение
Основные фонды по полной восстановительной стоимости на начало года	300
Степень износа основных фондов на начало года, %	30
введено новых основных фондов за год	50
Выбыло основных фондов по полной стоимости	30
Остаточная стоимость выбывших основных фондов, %	45
Сумма начисленного износа за год	25
Затраты на капитальный ремонт за год	18

Определите:

1) полную восстановительную стоимость на конец года

2) восстановительную стоимость за вычетом износа на начало и конец года

3) Коэффициенты годности основных фондов на начло и конец года

4) коэффициенты износа основных фондов на конец года

5) коэффициенты обновления и выбытия основных фондов

РЕШЕНИЕ

1) Полная восстановительная стоимость на конец года:

300+50-30 = 320 (млрд. руб.)

2) Восстановительная стоимость за вычетом износа

На начало года: 300-300*0,3 = 210 (млрд. руб.)

На конец года: 210+50-16,5-25 = 328,5 (млрд. руб.)

3) Коэффициент годности:

На начало года: 210/300 =0,7

На конец года: 295/320=0,92

4) Коэффициент износа на конец года:

25*100/320 = 7,81 %

5) Коэффициент обновления:

50/300 = 0,17

6) Коэффициент выбытия:

30/300 = 0,1

Таблица 13

Баланс по полной восстановительной стоимости

Показатель	Значение, млрд. руб.
На начало года	300
Поступило	50
Выбыло	30
На конец года	320

Таблица 14

Баланс по восстановительной стоимости за вычетом износа

Показатель	Значение, млрд. руб.
На начало года	210
Поступило	50
Выбыло	16,5
На конец года	328,5

Задача 9

УСЛОВИЕ ЗАДАЧИ

За отчетный период имеются данные о распределении домохозяйств региона по размеру среднедушевых денежных доходов

Таблица 15

Среднедушевой денежный доход, руб.	Число домохозяйств, %	Численность населения, %
До 800	6,5	7,5
800-1200	29,3	23,4
1200-1600	21,6	21,7
1600-2000	11,4	13,5
2000-2400	9,1	8,4
2400-2800	8,3	7,3
2800-3200	7	6,7
3200-3600	3,1	2,5
3600 и более	3,7	9
ИТОГО	100	100

Определить:

1) среднедушевой месячный доход населения

2) модальные и медианные размеры среднедушевых месячных доходов населения региона

3) показатели дифференциации и концентрации доходов населения региона

4) численность населения региона, имеющего доход ниже прожиточного минимума, установленного в размере 1530 руб.

5) уровень бедности

6) Постройте кривую Лоренца

РЕШЕНИЕ

1) среднедушевой доход населения

Таблица 16

Интервальное значение	Срединное значение интервала (х)	Численность населения, % (у)	х*у
До 800	600	7,5	4500
800-1200	1000	23,4	23400
1200-1600	1400	21,7	30380
1600-2000	1800	13,5	24300
2000-2400	2200	8,4	18480
2400-2800	2600	7,3	18980
2800-3200	3000	6,7	20100
3200-3600	3400	2,5	8500
3600 и более	3800	9	34200
ИТОГО		100	182840

Среднедушевой доход:

182840 / 100 = 1828, 4 (руб.)

2) Модальное значение среднедушевого дохода:

Модальный интервал: 800-1200

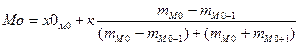
х0_М0 = 800 – нижняя граница модального интервала

m_M₀= 23,4 – частота модального интервала

m_M_0-1= 7,5 – частота предмодального интервала

m_M₀₊₁= 21,7 – величина послемодального интервала

к = 400 – величина модального интервала

Мо =800+400*(23,4-7,5)/(23,4-7,5)+(23,4-21,7) = 800+400*0,9=1161

Таким образом, наиболее часто встречающееся значение среднедушевого дохода равно 1161 руб.

Медианный интервал- 2000-2400

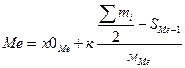
хо_Ме = 2000 – нижняя граница медианного интервала

к = 400 – величина медианного интервала

м_Ме= 8,4 – частота медианного интервала

S_ме-1= 66,1 – сумма накопленных частот до медианного интервала

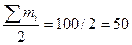
Тогда, медиана равна:

Ме= 2000+400*(50-66,1)/8,4 = 1233 (руб.)

Таким образом, медиана равна 1233 руб.

3) Коэффициент Херфиндаля-Хиршмана есть сумма квадратов долей, занимаемых на рынке всеми действующими на нем группами населения.

Таблица 17

Расчет индекса Херфиндаля-Хиршмана

Численность населения, % (у)	Квадрат численности
7,5	56,25
23,4	547,56
21,7	470,89
13,5	182,25
8,4	70,56
7,3	53,29
6,7	44,89
2,5	6,25
9	81
100	1512,94

Коэффициент концентрации доходов населения равен отношению численности населения с доходами выше прожиточного минимума к общей численности населения.

Таблица 18

Расчет децильного коэффициента

Интервальное значение	Численность населения, % (у)	Численность населения, тыс. чел
1600-2000	13,5	391,61
2000-2400	8,4	243,67
2400-2800	7,3	211,76
2800-3200	6,7	194,35
3200-3600	2,5	72,52
3600 и более	9	261,07
ИТОГО	100	1374,98

Децильный коэффициент равен:

1374,98*100/806,5*3,2 = 53 (%)

4) Численность населения региона, имеющего доход ниже прожиточного минимума, установленного в размере 1530 руб.

Таблица 19

Интервальное значение	Численность населения, % (у)	Численность населения, тыс. чел.
До 800	6,5	167,75
800-1200	29,3	756,17
1200-1600	21,6	557,45
ИТОГО		1481,38

Численность населения, имеющего доход ниже прожиточного минимума равна 1481,38 тыс. человек.

Уровень бедности определяем отношением численности населения, имеющего доход ниже прожиточного минимума к общему количество человек в регионе: 1481,38*100/806,5*3,2 = 57,4 (%)

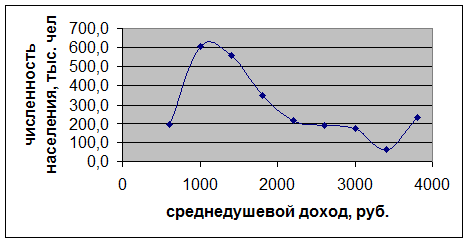
Рис. 5. Кривая Лоренца