Всероссийский Заочный Финансово-Экономический Институт
Кафедра экономико-математические
методы и модели
Аудиторная работа
по дисциплине "ЭММ и
ПМ"
Вариант №5
Студента:
Факультет: У/С
Группа: № 336
№ зачетной книжки: 02УБД9125
Преподаватель: Гармаш А.Н.
Москва-2005
Задача 1.5.
Выбор оптимальных проектов для финансирования.
Управляющему банка были
предоставлены 4 проекта, претендующие на получение кредита в банке. Доступная
наличность банка, потребности проектов и прибыль по ним приведены в таблице
(тыс.дол.).
|
Проект
|
Период 1
|
Период 2
|
Период 3
|
Период 4
|
Прибыль
|
|
А
|
8
|
8
|
10
|
10
|
21
|
|
В
|
7
|
9
|
9
|
11
|
18
|
|
С
|
5
|
7
|
9
|
11
|
16
|
|
D
|
9
|
8
|
7
|
6
|
17.5
|
|
Ресурс банка
|
22
|
25
|
38
|
30
|
|
При оценке этих предложений
следует принять во внимание потребность проектов в наличности и массу доступной
наличности для соответствующих периодов.
Какие проекты следует финансировать и
какое количество наличности необходимо в течении каждого периода, если цель
состоит в том, чтобы максимизировать прибыль?
Решение.
Построим ЭММ задачи, для этого введем необходимые
обозначения:
Пусть Х1,Х2,Х3,Х4-это объем прибыли по каждому проекту.
Х=( Х1,Х2,Х3,Х4) с учетом этих обозначений ЭММ задачи имеет
вид
max f ( Х1,Х2,Х3,Х4)= 21 Х1+18
Х2+16 Х3+17.5
Х4
При ограничениях:
8 Х1+7 Х2+5 Х3+9 Х4<=22
8 Х1+9 Х2+7 Х3+8 Х4<=25
10 Х1+9 Х2+9 Х3+7 Х4<=38
10 Х1+11 Х2+11 Х3+6 Х4<=30
Х1,Х2,Х3,Х4>=0
Ограничения по объемам запасов соответствующих ресурсов.
В этой модели целевая функция это математическая запись
критерия оптимальности «максимум прибыли от финансирования проекта»
Реализация модели этой задачи может быть осуществлено
средствами Excel с
использованием программы оптимизации («поиск решения»)
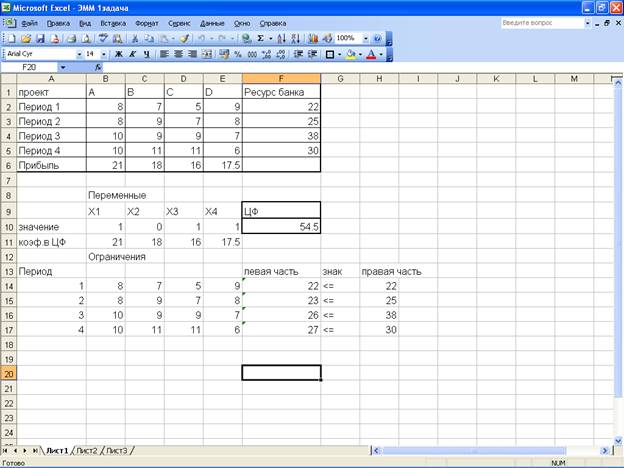
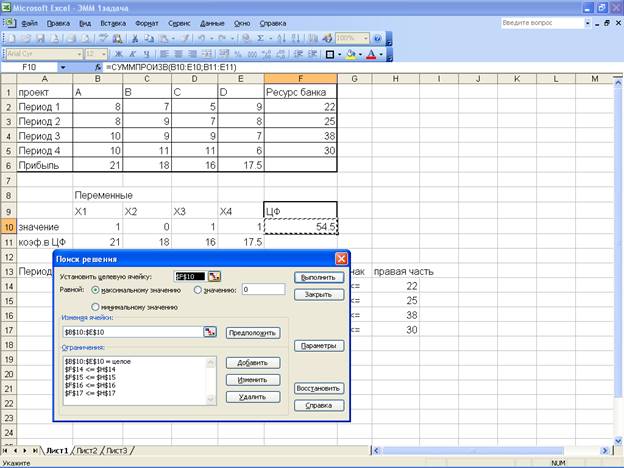
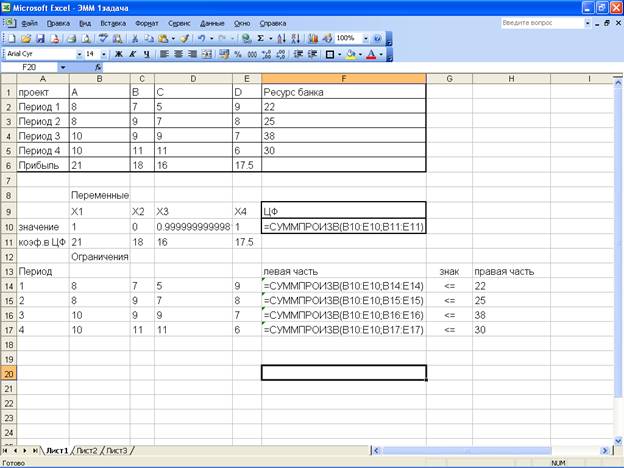
Вывод: в результате нами был получен оптимальный план
финансирования. Таким образом в данной ситуации для получения максимальной
прибыли равной 54,5 тыс.дол. целесообразно финансировать проекты А,С и D.
Для финансирования
данных проектов необходимо количество наличности в течении каждого периода:
В первом периоде
необходимо 22 тыс.дол.
Во втором периоде
необходимо 23 тыс.дол.
В третьем периоде
необходимо 26 тыс.дол.
В четвертом периоде
необходимо 27 тыс.дол.
Задача 2.5
Закрепление самолетов за воздушными линиями.
Три типа самолетов требуются
распределить между четырьмя авиалиниями. В приводимых ниже таблицах заданы
число самолетов каждого типа, месячный объем перевозок каждым самолетом на
каждой авиалинии и соответствующие эксплуатационные расходы.
Требуется
распределить самолеты по авиалиниям так, чтобы при минимальных суммарных
эксплуатационных расходах перевезти по каждой из четырех авиалиний
соответственно не менее 300, 200, 1000 и 500 ед. груза.
|
Тип самолета
|
Число самолетов
|
Месячный объем
перевозок одним самолетом по авиалиниям
|
|
|
|
I
|
II
|
III
|
IV
|
|
|
1
|
50
|
15
|
10
|
20
|
50
|
|
|
2
|
20
|
30
|
25
|
10
|
17
|
|
|
3
|
30
|
25
|
50
|
30
|
45
|
|
|
|
|
|
|
|
|
|
Тип самолета
|
Эксплуатационные
расходы
|
|
|
|
I
|
II
|
III
|
IV
|
|
|
|
1
|
15
|
20
|
25
|
40
|
|
|
|
2
|
70
|
28
|
15
|
45
|
|
|
|
3
|
40
|
70
|
40
|
65
|
|
|
Решение.
Построим ЭММ задачи, для этого введем необходимые
обозначения:
Пусть Хij(i=1,2,3;j=1,2,3,4)-месячный объем перевозок по
авиалиниям(от i-ого
самолета к j-той
авиалинии)
Таким образом мы рассматриваем матрицу перевозок вида (план
прикрепления самолетов к авиалиниям): получается матрица
|
Х(хij)3х4=
|
Х11
|
Х12
|
Х13
|
Х14
|
|
Х21
|
Х22
|
Х23
|
Х24
|
|
Х31
|
Х32
|
Х33
|
Х34
|
С учетом этих обозначений ЭММ рассматриваемой транспортной
задачи имеет вид
min(15
Х11+20 Х12+25
Х13+40 Х14+70
Х21+28 Х22+15
Х23+45 Х24+40
Х31+70 Х32+40
Х33+65 Х34)
при ограничениях:
Х11+ Х12+ Х13+ Х14=50
Х21+ Х22+ Х23+ Х24=20
Х31+ Х32+ Х33+ Х34=30
Ограничения означают объем перевозок вывозимые каждым
самолетом.
Х11+ Х21+ Х31=>300
Х12+ Х22+ Х32=>200
Х13+ Х23+ Х33=>1000
Х14+ Х24+ Х34=>500
Ограничения означают объем перевозок по каждой авиалинии
Хij>0(i=1,2,3;j=1,2,3,4)
В приведенной модели целевая функция это математическая
запись критерия оптимальности «минимум суммарных эксплуатационных расходов
перевозок по авиалиниям».
Реализация модели этой задачи может быть осуществлено
средствами Excel с
использованием программы оптимизации («поиск решения»)
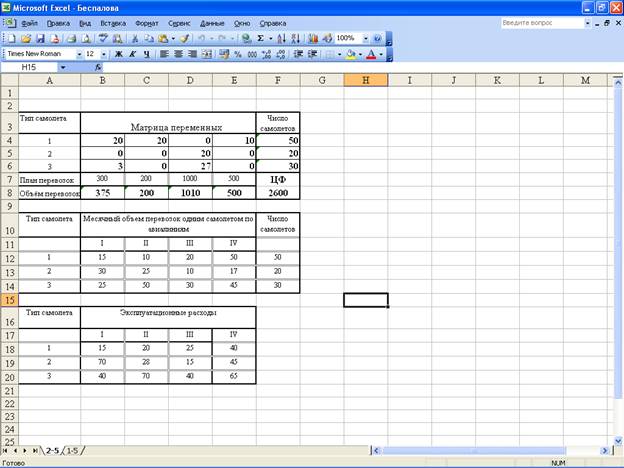
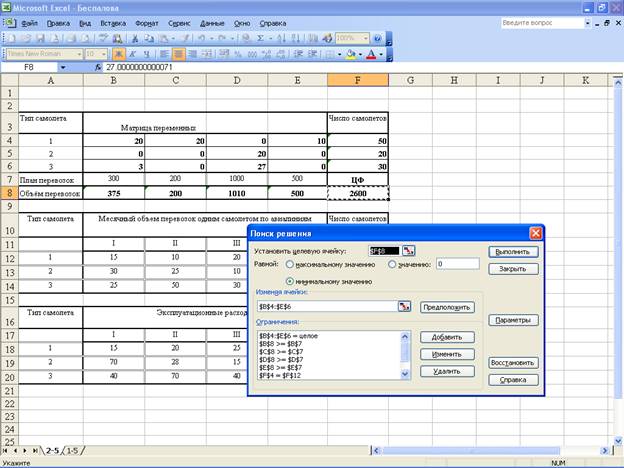
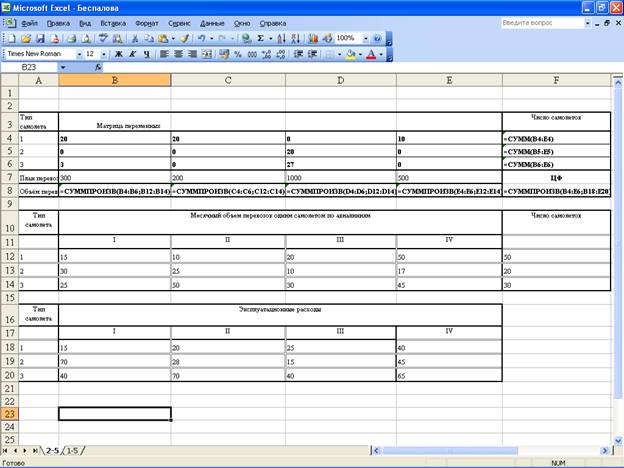
Вывод: в результате нами был получен оптимальный план
перевозок. План перевозок означает что при минимальных суммарных
эксплуатационных расходах равным 2600ед. груза, самолеты следует распределить
так:
Х11= 20 самолетов 1-го
типа следует отправить по первой авиалинии,
Х31= 3 самолета 3-го
типа следует отправить по первой авиалинии,
Х12= 20 самолетов 1-го
типа следует отправить по второй авиалинии,
Х23= 20 самолетов 2-го
типа следует отправить по третьей авиалинии,
Х33= 27 самолетов 3-го
типа следует отправить по третьей авиалинии,
Х14= 10 самолетов 1-го
типа следует отправить по четвертой авиалинии.