МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВСЕРОССИЙСКИЙ
ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА ЭКОНОМИКО-МАТЕМАТИЧЕСКИХ МЕТОДОВ И МОДЕЛЕЙ
К О Н Т Р О Л Ь Н А
Я Р А Б О Т А
по э к о н о м е т р и к е
Вариант 17
Выполнила:
студентка III
курса Оксана
специальность
Проверил:
должность доц. Уродовских В. Н.
__________________
подпись
Липецк 2006
Задача 1.
Предприятие легкой промышленности
региона характеризуется объемом выпуска продукции y (млн. руб.) и объемом
капиталовложений x (млн. руб.).
Требуется:
1)
Построить
уравнение линейной регрессии, дать экономическую интерпретацию его
коэффициентов.
2)
Вычислить
остатки, построить их график; найти остаточную сумму квадратов; оценить
дисперсию S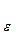 .
.
3)
Проверить
выполнение предпосылок МНК.
4)
Проверить
значимость параметров уравнения по t-критерию Стьюдента при 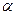 =0,05.
=0,05.
5)
Вычислить
коэффициент детерминации R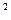 ,
проверить значимость уравнения по F-критерия, найти среднюю
относительную ошибку аппроксимации, оценить качество модели.
,
проверить значимость уравнения по F-критерия, найти среднюю
относительную ошибку аппроксимации, оценить качество модели.
6)
Выполнить
прогноз среднего значения показателя y при 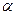 =0,10, если Х
=0,10, если Х составляет 80% от его
максимального значения.
составляет 80% от его
максимального значения.
7)
Представить
графически: фактические, модельные значения и точки прогноза.
8)
Составить
уравнения нелинейной регрессии:
- гиперболической;
- степенной;
- показательной.
9) Привести графики всех построенных уравнений
регрессии.
10) Для указанных моделей найти
коэффициенты детерминации и средние относительные ошибки аппроксимации.
Сравнить модели по этим характеристикам и сделать вывод.

РЕШЕНИЕ:
1.Построим уравнение линейной регрессии, дадим экономическую
интерпретацию его коэффициентов.
Уравнение линейной регрессии имеет
вид:
y = a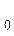 + a
+ a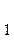
Для расчета построим вспомогательную
таблицу:
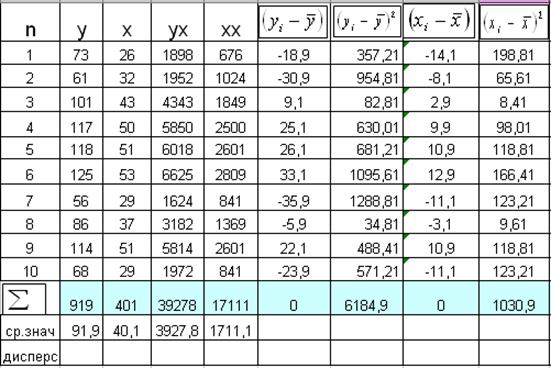
Найдем значения параметров модели:
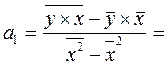

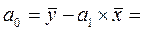 91,9-2,35
91,9-2,35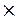 40,1 = 91,9 - 94,235 = -2,34
40,1 = 91,9 - 94,235 = -2,34
Уравнение линейной модели имеет вид:
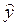 = -2,34 + 2,35х
= -2,34 + 2,35х
Рассчитаем линейный коэффициент парной
корреляции:
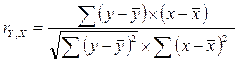
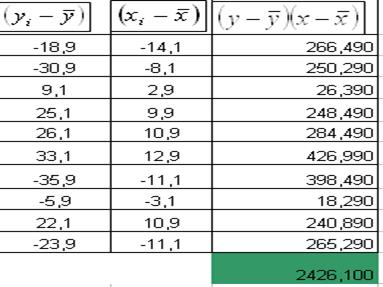
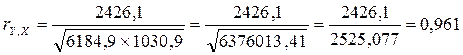
Вывод: Связь
между объемом капиталовложений Х и объемом выпуска продукции Y достаточно сильная и прямая. 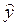 = -2,34 + 2,35х
= -2,34 + 2,35х
С увеличением объема капиталовложений
Х на 1 млн. руб. объем выпускаемой продукции Y увеличится в среднем на 2350 тыс.
руб., что свидетельствует о достаточно эффективной работе предприятия.
2.Вычислим остатки, построим их график; найдем остаточную сумму
квадратов; оценим дисперсию S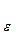 .
.
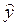 = -2,34 + 2,35х Подставляя в уравнение регрессии фактические значения х, определим расчетные значения
= -2,34 + 2,35х Подставляя в уравнение регрессии фактические значения х, определим расчетные значения  .
.
Построим вспомогательную таблицу:
Параметры модели определяем в Excel с помощью инструмента Регрессия (Сервис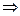 Анализ данных
Анализ данных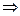 Регрессия)
Регрессия)
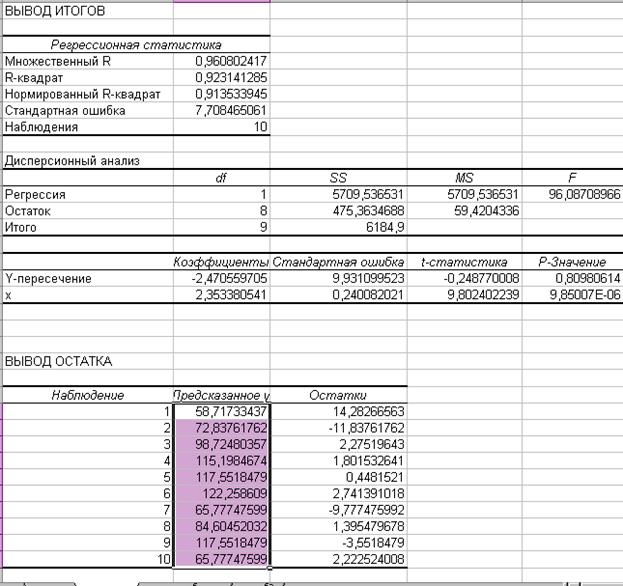
В таблице ВЫВОД ОСАТКА приведены вычисленные (предсказанные) по модели
значения зависимой переменной Y и значения остаточной компоненты Еi.
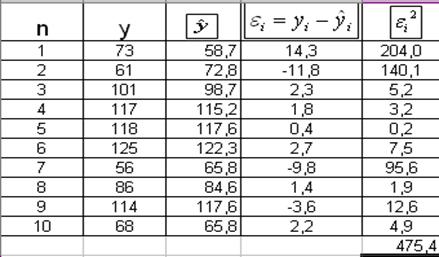
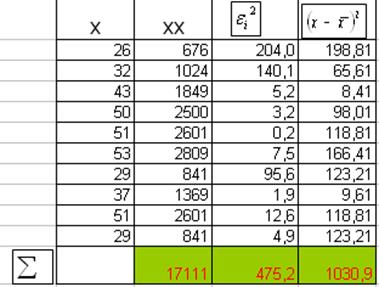
Для
парной регрессии дисперсия остатков:
Sε2 = 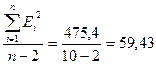
График остатков выглядит следующим
образом:
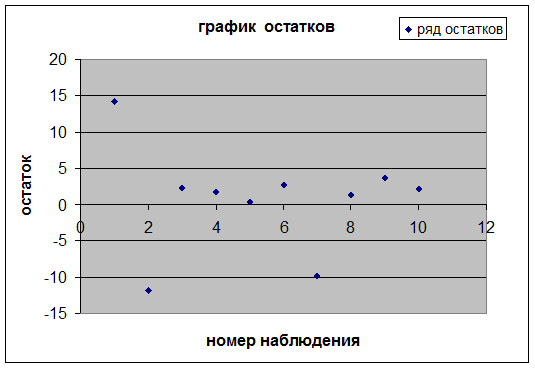
3.Проверим выполнение предпосылок МНК.
- Отсутствие
автокорреляции (остатки распределены
независимо друг от друга)
Отсутствие автокорреляции
(зависимость остатков 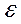 ) проверяется по d-критерию Дарбина - Уотсона:
) проверяется по d-критерию Дарбина - Уотсона:
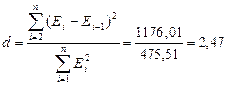
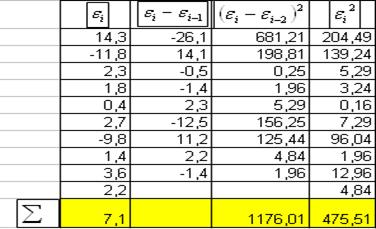
d1 =1,08
d2 =1,36
Т.к.d>2, то d – критерий пересчитывается по
формуле: 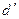 = 4-d
= 4-d
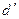 = 4-2,47 = 1,53
= 4-2,47 = 1,53
Т.к. d2 < 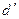 < 2, то ряд остатков не коррелирован.
< 2, то ряд остатков не коррелирован.
- Случайный характер остатков (проверяется по графику)
Из графика видно, что в расположении
точек нет направленности, следовательно 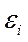 - случайные величины.
- случайные величины.
- Проверка равенства
математического ожидания нулю
Выполняется по t-критерию Стьюдента
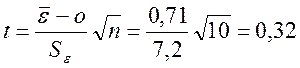
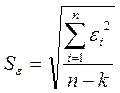
tтабл=2,26,следовательно рассчитанное значение
меньше его табличного, значит гипотеза о равенстве нулю математического
ожидания принимается.
- Обнаружение
гетероскедастичности
Выявляем при
помощи Теста Голдфельда-Квандта:
- Ранжируем наблюдения в порядке возрастания Х
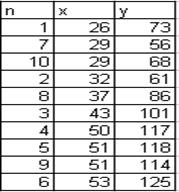
- Делим все наблюдения на две группы и для
каждой из них определяем уравнение регрессии:
1. Для первой группы
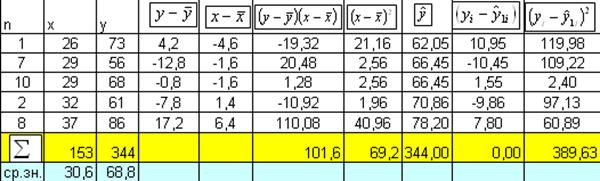
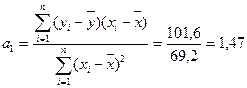
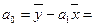 68,8-1,47*30,6 = 23,8
68,8-1,47*30,6 = 23,8
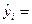 23,8 + 1,47x
23,8 + 1,47x
2. Для второй группы
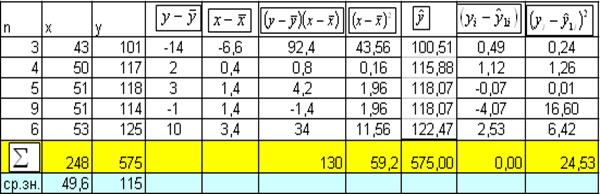
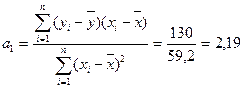
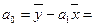 115-2,19*49,6 = 6,08
115-2,19*49,6 = 6,08
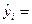 6,08 +2,19x
6,08 +2,19x
- Определим остаточную сумму квадратов для
первой регрессии:
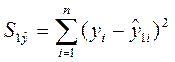 =389,63
=389,63
И
для второй:
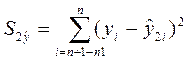 =24,53
=24,53
Вычислим отклонение 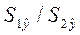 , в числителе должна быть большая сумма квадратов:
, в числителе должна быть большая сумма квадратов:
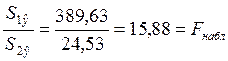
Полученное отклонение имеет F-распределение со степенями
свободы k1 = n1 - m и k2 = n – n1 - m (m – число оцениваемых параметров в
уравнении регрессии).
k1
= 3 k2
=10-5-2 = 3
Fнабл (α; k1;
k2) = 15,88
Fтабл (0,05; 3; 3) = 9,27
Fнабл > Fтабл, следовательно гетероскедастичность
имеет место.
4.Проверим значимость параметров
уравнения по t-критерию Стьюдента при 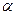 =0,05.
=0,05.
Выдвигается Н0 – гипотеза о незначимом отличии параметра уравнения регрессии от
нуля. Для проверки этой гипотезы используется t-статистика. Расчетные значения t-критерия определяются по формулам:
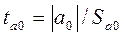
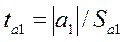
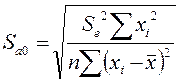
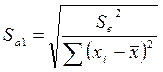
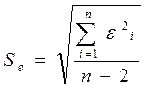
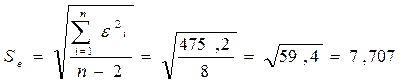
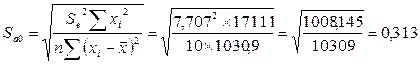
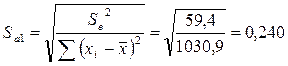
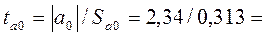 7,47
7,47
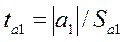 = 2,35 / 0,24
= 9,79
= 2,35 / 0,24
= 9,79
tтабл =2,3
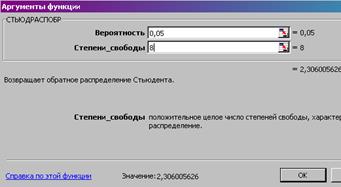
Т.к. tрасч>tтабл (7,47>2,3), то коэффициент а0
значим, tрасч<tтабл (9,79>2,3), то коэффициент а1
тоже значим.
5. Вычислим коэффициент детерминации R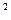 , проверим значимость уравнения по F-критерию, найдем
среднюю относительную ошибку аппроксимации, оценим качество модели.
, проверим значимость уравнения по F-критерию, найдем
среднюю относительную ошибку аппроксимации, оценим качество модели.
-  1-0,077=0,923
1-0,077=0,923
Данный коэффициент показывает долю
вариации результативного признака под воздействием изучаемых факторов.
Следовательно, около 92% вариации зависимой переменной учтено в модели и
обусловлено влиянием включенных факторов.
- Проверку значимости уравнения регрессии произведем на основе вычисления F-критерия Фишера:
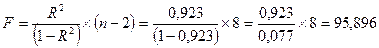
Табличное значение F-критерия при доверительной
вероятности 0,05 при v1=К=1 и v2=n-k-1=10-1-1=8 составляет
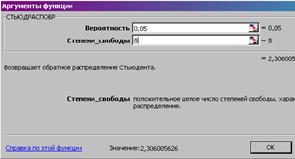
Fтабл = 2,3
Поскольку Fрас>Fтабл, уравнение регрессии следует
признать значимым.
- Найдем среднюю относительную ошибку
аппроксимации и оценим качество модели:
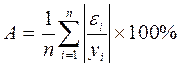
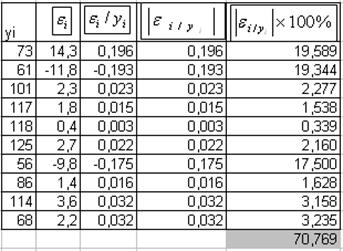
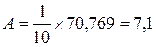
A практически равно 7, следовательно
модель имеет хорошее качество.
6. Выполним прогноз среднего
значения показателя y при 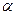 =0,10, если Х
=0,10, если Х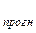 составляет 80% от его
максимального значения.
составляет 80% от его
максимального значения.
хпр = 0,8*хmax = 0,8*53 = 42,4
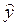 пр= -2,34 + 2,35*42,4 = 97,3
пр= -2,34 + 2,35*42,4 = 97,3
Стандартная ошибка:
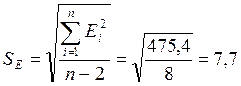
Коэффициент Стьюдента tα для m = 10-2 = 8 степеней свободы и уровня
значимости 0,1: tтабл = 1,8595
Тогда u(x=36.8; n=10; α=0.1) = 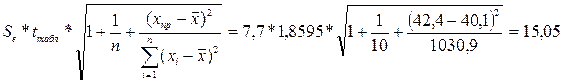
Верхняя граница: уmax = 97,3 + 15,05 = 112,35
Нижняя граница: ymin = 97,3 - 15,05 = 82,25
Диапазон верхней и нижней границ доверительного интервала
∆у:
∆у =112,35 /82,25 = 1,3
Вывод: выполненный прогноз объема выпуска
продукции оказался надежным (ρ = 1 - α = 1 - 0,1 = 0,9), но не
точным, т.к. диапазон верхней и нижней границ доверительного интервала ∆у
= 1,3
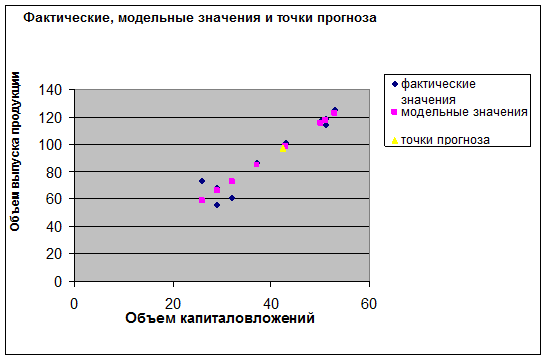
7.Представим графически: фактические, модельные значения и точки
прогноза.
8. Составим уравнения нелинейной
регрессии:
- гиперболической;
- степенной;
- показательной.
. Гиперболическая модель.
Уравнение гиперболической
модели: 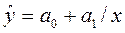
Для построения этой модели произведем
ее линеаризацию путем замены переменных: X = 1/x
Получим линейное уравнение регрессии:
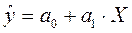
Далее рассчитаем параметры модели.
Для расчета параметров построим
вспомогательную таблицу:
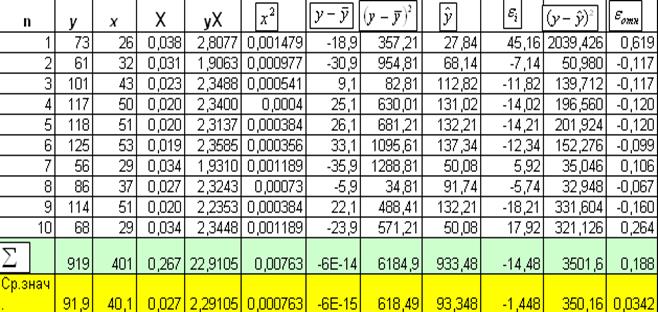
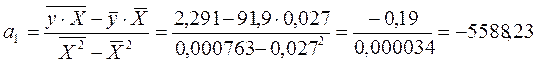
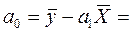 91,9 +5588,23*0,027=242,78
91,9 +5588,23*0,027=242,78
Запишем гиперболическую модель:
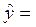 242,78 - 5588,23/x
242,78 - 5588,23/x
Рассчитаем индекс корреляции:
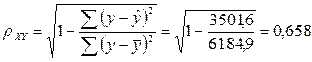
Связь между показателем y и фактором x можно считать не очень сильной.
Рассчитаем индекс детерминации: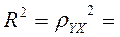 0,658*0,658=0,433
0,658*0,658=0,433
Вариация объема выпуска продукции у
на 43,3% объясняется вариацией фактора х - объема капиталовложений.
Рассчитаем F-критерий Фишера:
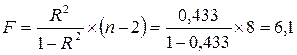
Поскольку F>Fтабл= 5,11 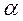 =0,05; к1=m=1, к2=n-m=9 , то уравнение регрессии с
вероятностью 0,95 в целом статистически
значимо.
=0,05; к1=m=1, к2=n-m=9 , то уравнение регрессии с
вероятностью 0,95 в целом статистически
значимо.
Рассчитаем среднюю относительную
ошибку аппроксимации:
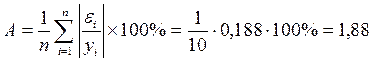
В среднем расчетные значения урасч
гиперболической функции отличаются от фактических значений на 1,88%.
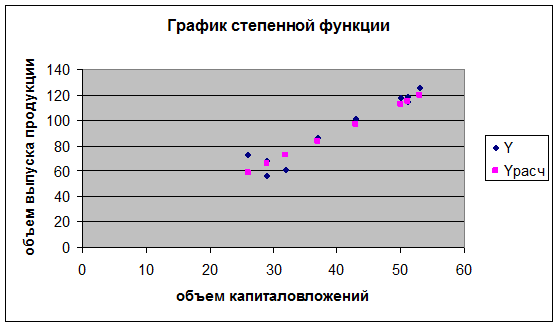
2. Степенная модель.
Степенная модель имеет вид:
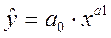
Произведем линеаризацию уравнения
путем логарифмирования его обеих частей:
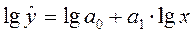
Обозначим: 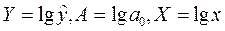
С учетом этого получим линейное
уравнение регрессии:
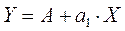
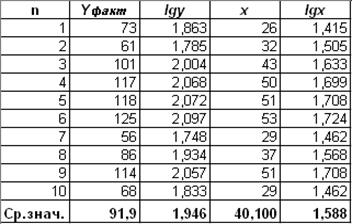
Для расчета параметров построим
вспомогательную таблицу:
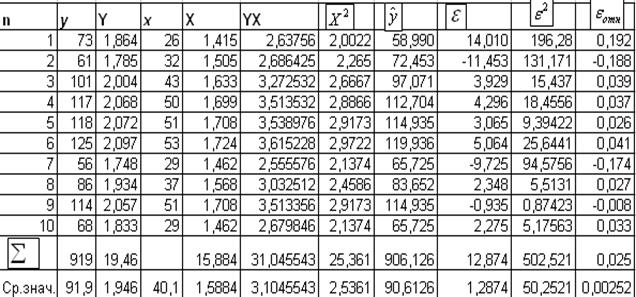
Найдем значения параметров модели:
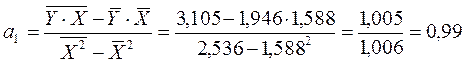
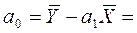 1,946-0,99*1,588=0,37
1,946-0,99*1,588=0,37
Уравнение регрессии будет иметь вид:
Y= 0,37+0,99X
Перейдем к исходным переменным x и y, выполнив потенцирование последнего
уравнения: 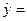
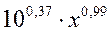
Тогда окончательно имеем уравнение
степенной модели:
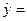
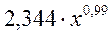
Определим индекс корреляции:
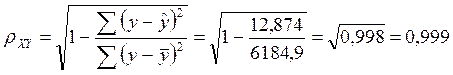
Связь между показателем y и фактором x можно считать очень сильной.
Рассчитаем индекс детерминации:
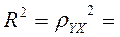 0,999*0,999=0,998
0,999*0,999=0,998
Вариация объема выпуска продукции у
на99,8% объясняется вариацией фактора х - объема капиталовложений.
Рассчитаем F-критерий Фишера:
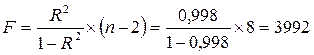
Поскольку F>Fтабл=5,11 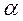 =0,05; к1=m=1, к2=n-m= 9 , то уравнение регрессии с
вероятностью 0,95 в целом статистически
значимо.
=0,05; к1=m=1, к2=n-m= 9 , то уравнение регрессии с
вероятностью 0,95 в целом статистически
значимо.
Рассчитаем среднюю относительную
ошибку аппроксимации:
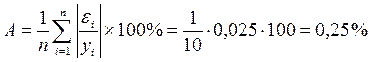
В среднем расчетные значения урасч
степенной функции отличаются от фактических значений на 0,25%.
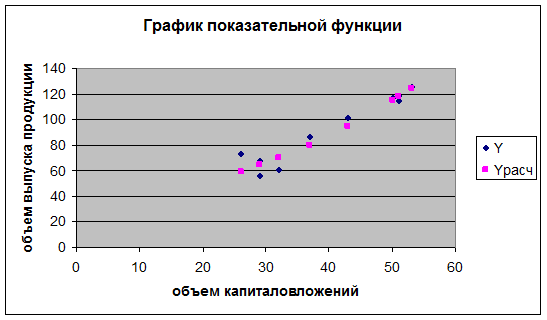
3. Показательная модель.
Уравнение показательной кривой: 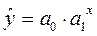
Для построения этой модели произведем
линеаризацию путем логарифмирования обеих частей уравнения: 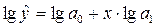
Обозначим 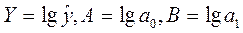
Получим линейное уравнение регрессии:
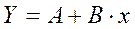
Далее рассчитаем параметры модели.
Для расчета параметров построим
вспомогательную таблицу:
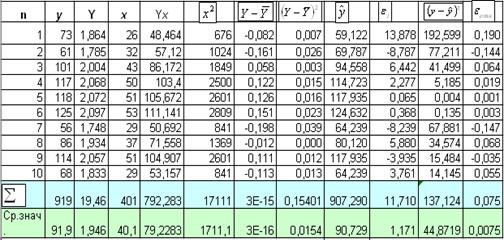
Найдем значения параметров модели:
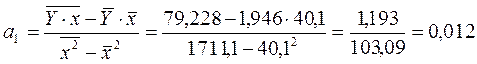
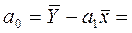 1,946-0,012*40,1=1,46
1,946-0,012*40,1=1,46
Уравнение регрессии будет иметь вид:
Y= 1,46 + 0,012x
Перейдем к исходным переменным x и y, выполнив потенцирование последнего
уравнения: 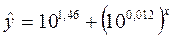
Тогда окончательно имеем уравнение
степенной модели:
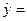 28,84*1,028
28,84*1,028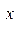
Определим индекс корреляции:
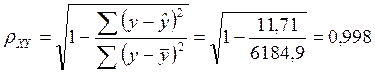
Связь между показателем y и фактором x можно считать очень сильной
Рассчитаем индекс детерминации:
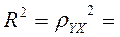 0,998*0,998=0,996
0,998*0,998=0,996
Вариация объема выпуска продукции у
на 99,6% объясняется вариацией фактора х - объема капиталовложений.
Рассчитаем F-критерий Фишера:
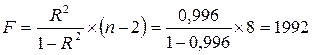
Поскольку F>Fтабл= 5,11 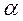 =0,05; к1=m=1, к2=n-m=9 , то уравнение регрессии с
вероятностью 0,95 в целом статистически
значимо.
=0,05; к1=m=1, к2=n-m=9 , то уравнение регрессии с
вероятностью 0,95 в целом статистически
значимо.
Рассчитаем среднюю относительную
ошибку аппроксимации:
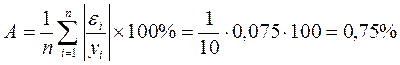
 В среднем расчетные значения урасч показательной функции
отличаются от фактических значений на 0,75%.
В среднем расчетные значения урасч показательной функции
отличаются от фактических значений на 0,75%.
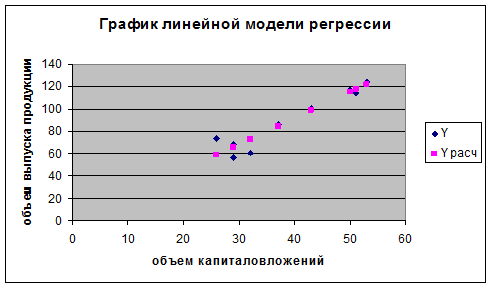
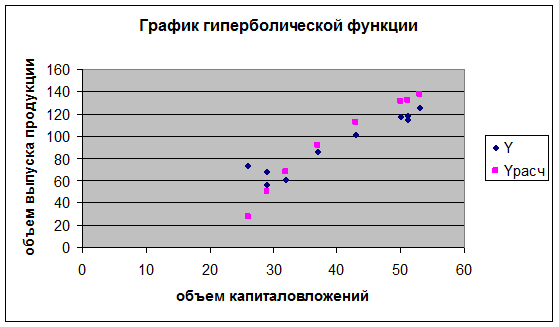
9.
Приведем графики всех построенных уравнений регрессии.
10. Для указанных моделей найдем
коэффициенты детерминации и средние относительные ошибки аппроксимации. Сравним
модели по этим характеристикам и сделаем
вывод.

Из сводной таблицы результатов
расчета видно, что наиболее лучшие характеристики имеет степенная модель,
поэтому ее выбираем для построения прогноза.
Задача 2
Задача 2а и 2б .
Имеются два варианта структурной формы модели заданные в виде
матриц коэффициентов модели. Необходимо для каждой матрицы записать системы
одновременных уравнений и проверить их на идентифицируемость.
2а

Составим системы
одновременных уравнений:
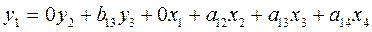
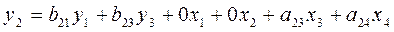
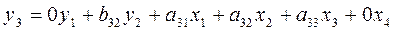
Проверим каждое уравнение на
выполнение необходимых и достаточных условий идентификации.
Первое уравнение: 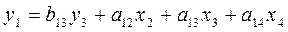
Определим эндогенные переменные: y1,
y3, т.е. Н
= 2,
Найдем отсутствующие экзогенные
переменные: x1, т.е. D = 1.
Проверяем условие идентификации 1+1 =
2 или D + 1 = Н – условие необходимости выполнено,
и уравнение можно считать идентифицируемым.
Далее проверяем достаточное условие.
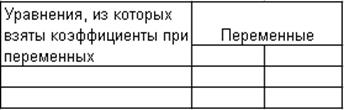
Определитель матрицы не равен нулю, следовательно, уравнение
можно считать идентифицируемым.
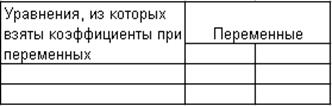
Второе уравнение: 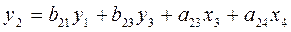
Определим эндогенные переменные: y1, y2, y3, т.е. Н = 3,
Найдем отсутствующие экзогенные
переменные: x1, x2 т.е. D = 2.
Проверяем условие идентификации 2+1 =
3 или D + 1 = Н – условие необходимости выполнено,
и уравнение можно считать идентифицируемым.
Далее проверяем достаточное условие.
Определитель матрицы не равен нулю,
следовательно, уравнение можно считать идентифицируемым.
Третье уравнение: 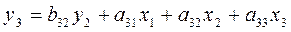
Определим эндогенные переменные:y2, y3, т.е. Н = 2,
Найдем отсутствующие экзогенные
переменные:x4 т.е. D = 1.
Проверяем условие идентификации 1+1 =
2 или D + 1 = Н – условие необходимости
выполнено и уравнение можно считать идентифицируемым.
Далее проверяем достаточное условие.
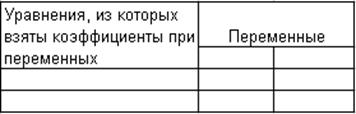
Определитель матрицы не равен нулю,
следовательно, уравнение можно считать идентифицируемым.
2б

Составим системы
одновременных уравнений:
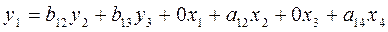
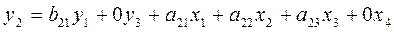
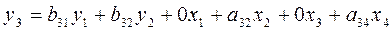
Проверим каждое уравнение на
выполнение необходимых и достаточных условий идентификации.
Первое уравнение 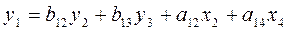
Определим эндогенные переменные: y1,y2, y3, т.е. Н = 3,
Найдем отсутствующие экзогенные
переменные:x1, x3 т.е. D = 2.
Проверяем условие идентификации 2+1 =
3 или D + 1 = Н – условие необходимости
выполнено и уравнение можно считать идентифицируемым.
Далее проверяем достаточное условие.

Поскольку вторая строка матрицы состоит из нулей, то ее
определитель равен нулю. Значит достаточное условие идентифицируемости не
выполнено и первое уравнение в СФМ нельзя
считать идентифицируемым.
Второе уравнение 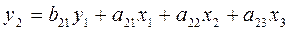
Определим эндогенные переменные: y1,y2 т.е. Н = 2,
Найдем отсутствующие экзогенные
переменные:x4 т.е. D = 1.
Проверяем условие идентификации 1+1 =
2 или D + 1 = Н – условие необходимости
выполнено и уравнение можно считать идентифицируемым.
Проверяем условие достаточности по
переменным y3 и x4.

Поскольку третье уравнение можно
записать в виде:
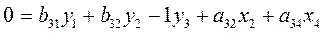 , тогда равенство
, тогда равенство 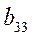 = -1 становится очевидным. Определитель для второй матрицы не
равен нулю а ранг матрицы равен ,
поэтому условие достаточности выполнено и это уравнение идентифицируемо.
= -1 становится очевидным. Определитель для второй матрицы не
равен нулю а ранг матрицы равен ,
поэтому условие достаточности выполнено и это уравнение идентифицируемо.
Третье уравнение: 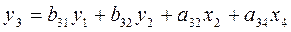
Определим эндогенные переменные: y1,y2, y3 т.е. Н = 3,
Найдем отсутствующие экзогенные
переменные:x1 ,x3
т.е. D = 2.
Проверяем условие идентификации 2+1 =
3 или D + 1 = Н – условие необходимости
выполнено и уравнение можно считать идентифицируемым.
Проверяем условие достаточности по
переменным, для чего строим матрицу для переменных x1 ,x3,
которые отсутствуют в третьем уравнении.

Определитель матрицы равен нулю
(первая строка представлена нулями), значит достаточное условие не выполнено, и
третье уравнение нельзя считать идентифицируемым.
Задача 2в
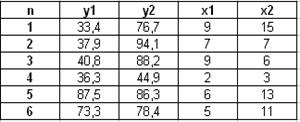
По данным таблицы для своего
варианта, используя косвенный метод наименьших квадратов (КМНК), построить
структурную форму модели вида:
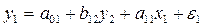
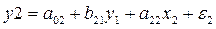
Структурная форма модели
преобразуется в приведенную. Для этого из 2-го уравнения выражаем у2 и
подставляем в первое уравнение, а из 1-го уравнения выражаем у1 и
подставляем во второе. После преобразований получаем:
у1 = δ11х1 + δ12х2
+ u1
у2 = δ21х1 + δ22х2
+ u2,
где u1 и u2 случайные ошибки ПФМ. Для 1-го
уравнения определим δ – коэффициенты с помощью традиционного МНК.
Σ у1x1 = δ11Σх12
+ δ12Σх1х2
Σ у1x2 = δ12Σх1х2
+ δ12Σх22
Расчетная таблица
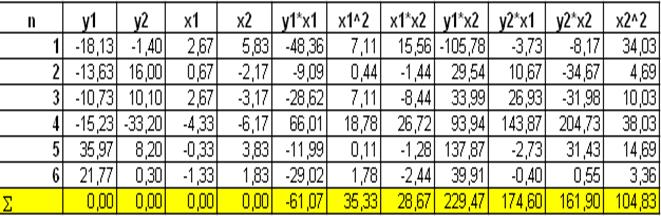
С учетом приведенных данных получаем:
-61,07 = 35,33 δ11 +
28,67 δ12;
229,47 = 28,67δ11 + 104,83 δ12
В результате решения получаем δ11 =
- 4,505 δ12 = 3,421
С учетом этого первое уравнение ПФМ
примет вид:
у1 = -4,505х1 +3,421х2 + u1
Для 2-го уравнения ПФМ с помощью МНК
определяем δ-коэффициенты:
Σ у2x1 = δ21Σх12
+ δ22Σх1х2
Σ у2x2 = δ21Σх1х2
+ δ22Σх22
Для дальнейших расчетов данные берем
из этой же таблицы. Подставляя значения сумм из таблицы, получим:
174,6 = 35,33 δ21
+28,67 δ22;
161,9 = 28,67 δ21 + 104,83 δ22 (для 2-го уравнения)
В результате решения получаем δ21
= 4,741 δ22 = 0,248
Второе уравнение ПФМ получаем в виде:
у2 = 4,741 х1 +0,248
х2 + u2
Выполним переход от приведенной формы
к структурной форме модели, для чего из последнего уравнения ПФМ найдем х2:
х2 = (у2 - 4,741
х1)/ 0,248
Подставим значение х2 в
первое уравнение ПФМ:
у1 = - 4,505х1
+3,421(у2 - 4,741 х1)/ 0,248 = 13,794у2 – 69,902х1
Таким образом,
b12
=13,794, a11 = - 69,902
Из первого уравнения ПФМ найдем х1:
х1 = (у1 +3,421х2)/ -4,505
Подставим выражение для х1
во второе уравнение ПФМ и найдем структурное уравнение:
у2 = 4,741 х1
+0,248 х2 + u2
у2 =4,741(у1
+3,421х2)/ -4,505 + 0,248 х2
= -1,052 у1 – 3,352 х2
Таким образом, b21 = -1,052 a22 = – 3,352
Свободные члены структурной формы
находим из уравнений:
а01 = у1,ср – b12y2,ср – a11x1,ср = 51,53 +13,794*78,1 + 69,902*6,33 =
1571,321
а02 = у2,ср – b21y1,ср – a22x2,ср = 78,1 + 1,052*51,53 + 3,352*9,17 = 163,047
Записываем СФМ в окончательном виде:
у1 = а01 + b12y2 + a11x1 + ε1 =1571,321–13,794 у2 - 69,902х1
+ ε1
у2 = а02 + b21y1 + a22x2 + ε2 = 163,047 - 1,052
у1 – 3,352х2 + ε2