Решение

Кривые спроса и предложения представлены на рис. 1

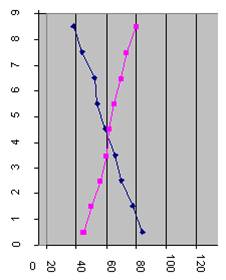
Рис.1 Кривые фактического и расчетного спроса и предложения

В этом случае расчетные значения спроса и (Qd) предложения (Qs) можно определить

(Qd) = а₀+а₁Р

(Qs) = b₀+b₁P

где а₀,а₁,b₀,b₁ – коэффициенты уравнений регрессии. Параметры а₀,а₁,b₀,b₁ определим, используя метод наименьших квадратов, согласно которому функция ошибка (сумма квадратов отклонений фактических значений ряда от теоретических) должна принимать минимальное значение. Для функции ошибок имеет следующий вид:

               N                   N

F(a₀,a₁) = ∑(Q_dn-Q_dn)² = ∑(Q_dn-(a₀+a₁P₀)² →min

              n=1                 n=1

Минимальное значение функции ошибок принимается в точке, где ее частные производные равны нулю, т.е.

dF(a₀a₁)/da₀ = 0

dF(a₀a₁)/da₁ = 0

Выполнив ряд преобразований из системы получим следующую систему

               N          N

a₀*N+a₁ = ∑Pn = ∑Q_dn

              n=1        n=1

     N           N       N

a₀*∑Pn+a₁ ∑P²n = ∑ P*Q_dn

     n=1        n=1   n=1

где N- количество наблюдений.

В нашем случае N=9, а вспомогательные суммы находим в таблице 2

Поставив необходимые значения в систему и решив е, получим а₀ = 414,4, а₁= 5,57. Таким образом, функция спроса имеет вид:

Qd = 414,4+5,57Р

Примечание полученное уравнение регрессии необходимо оценить с точки зрения его точности, надежности и значимости. Соответствующею теоретическую базу для этого можно найти в много численных источниках, посвященных корреляционно – регрессивному анализу данных,. Мы ограничимся напоминанием некоторых формул и вычеслением по ним значений для нашей задачи.

Остаточная дисперсия (σ²ост) коэффициент детерминации (R²) и значение критерия Фишера (F) вычисляются следующим образом

            N            

σ²ост = ∑(Q_dn-Q_dn)² /N-m-1

           n=1

R² = 1- σ²ост/ σ²Qd

      N                     N

F = ∑(Q_dn-Q_dn)² *m/∑(Q_dn-Q_dn)² (n-m-1)

     n=1                 n=1

где m- число независимых факторов, включенных в уравнение регрессии, Qd – средне значение объема спроса, σ²Qd – смещенная оценка дисперсии спроса.

В нашей задаче σ²ост = 1,47 R² = 0.469 F = 2930,99

Аналогичные вычисления проведем для определения функции предложения. Искомая функция имеет вид:

Qs = 935,5-4,08Р

Оценки этой функции следующие σ²ост = 0,60 R² = 0.468 F = 1983,648

3. Равновесную цену Ре и равновесный объем продаж Qе определим, зная что в точке равновесия совпадают цены спроса и предложения, а также объемы спроса и предложения т.е.

Ре = Рd-Ps

Qe = Qd-Qs

В нашей задаче при Qd-Qs из имеем

414,4+5,57Р=935,5-4,08Р. Отсюда равновесная цена Ре = 5,4

Равновесный объем спроса и предложения составит

414,4+5,57*5,4 = 71,5

Проверим по уравнению = 935,5-4,0*5,4 = 71,5

Таким образом, при установлении цены на уровне 5,4 у.д.е. объем спроса и предложения совпадут  и составят 71,5 тыс.шт. товар в месяц.

4. При установлении цены на уровне 5 уд.е. спрос составит

Qd = 414,4+5,57*5 = 69,3 тыс.шт. товара в месяц

Предложении при такой цене будет следующим:

Qs = 935,5-4,0*5 = 73,5 тыс.шт. товара в месяц. Таким образом, возникает профицит товара в 4,26 тыс.шт.

Установление цены выше равновесной, а именно на уровне 8 у.д.е., приведет к понижению объема предложения над спросом на 84,5 тыс.шт. (Qd =860, Qs = 615,5).

5. Наклон кривой спроса и предложения определяет возможность достижения точки равновесии. Так, «Паутина» сходится, если а₁>Ib₁I, расходится, если Ia₁I<Ib₁I, зацикливается, если Ia₁I=Ib₁I.

В нашем случае Ia₁I>Ib₁I возможно достижение точки равновесия.

Построим паутинообразную модель исходя из заданной цены. По условию, цена предшествующего периода была установлена на уровне 4 у.д.е., что определило предложение данного периода равным Qs = 935,5-4,0*4 = 77,5 тыс.шт. При таком предложении цена спроса устанавливается на уровне 21,3 у.д.е.

В свою очередь, цена Р=16,43 определит предложение последующего периода на уровне 81,2 тыс.шт. но потребитель такое количество товара согласен приобрести лишь при условии цены 6,9 у.д.е. Ориентируясь на цену 6,9 у.д.е., производитель в дальнейшем выпустит на рынок 57,9 тыс.шт. товара которые покупатель согласен приобрести по цене 5,4 у.д.е.  В конечном счете будет достигнута точка равновесия в п.3 задачи

Траектория изменения цен и количества предлагаемого и требуемого товара представлена на рис. 2

6. Эластичность спроса относительно цены находится по формуле.

Е_d = dQ_d/dP : Q_d/P

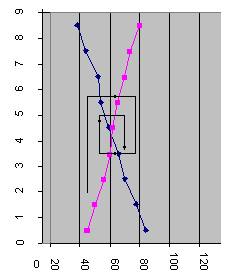
рис. 2 Паутинообразная модель.

В нашей задаче dQ_d/dP = а1 = 5,57. следовательно, в общем виде

Е_d = 5,57 : Q_d/P

Эластичность предложения по цене определяется по формуле

Е_s = dQ_s/dP : Q_s/P

В нашей задаче dQ_s/dP = а1 = -4, имеем эластичность предложения по цене равную Е_s = -4 : Q_s/P

Эластичность спроса и предложения показывает процентное изменение объема спроса или предложения меняется в зависимости от того, в какой точке «объемно-ценового» пространства мы находимся.

Спрос (предложение) эластичен при IЕ_dI > 1 (IЕ_sI >1) и неэластичен при IЕ_dI < 1 (IЕ_sI <1).

Значения эластичностей спроса и предложения по цене для разных уровней цены приведены в таблице 3.

Таблица 3

Эластичности спроса и предложения по цене. -4 : Q_s/P

Из таблицы 3 видно что спрос остается эластичным , т.е. растет быстрее, чем падает цена, до тех пор пол пока цена остается в приделах от остается

Эластичность предложения по цене меняется слабо и остается при любой из указанных цен меньше 1, т.е. предложение в рассматриваемом диапазоне цен растет медленнее, чем цены.

7. Перекрестная эластичность спроса рассчитывается по формуле.

Е_s = ∆Q_d*Q_s/∆PjPi

Где i, j – индексы товаров, ∆ Q_d – изменение объема спроса на I товар где ∆ P – изменение цены j – го товара,

Если Е > 0 то товары взаимозаменяемы, если Е <, то товары взаимодополняемы, если = 0 то товары независимы.

В нашей задаче

       60-80/80

Е = 10-12/12 = -0,25/-0,17 = 1,5

т.е. товары взаимозаменяемы, и снижение цены второго товара на 1% влечет за собой падение спроса на первый товар на 1,5 %.

Задача 2

В таблице 2 приведены данные по объему продаж продукции компании N за период с 1996 по 1999 г.

Таблица 4

Задание

1.     Нанести исходные данные на график

2.     выделить тренд с помощью трехточечных скользящих средних. Построить график.

3.     используя метод сложения (умножения), спрогнозировать объем продаж в каждом квартале 2000 г. Нанести на график полученные результаты.

Решение

1. Нанесем исходные данные на график (рис 3). Сходя из приведенных значении, можно сказать , что данные  объема продаж четко показывают

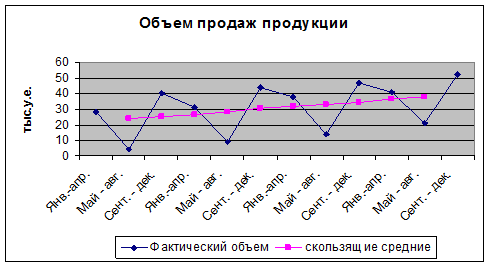
рис.3 Объем продаж

Заметим что объемы продаж имеют тенденцию к снижению в летний период и достигают пика в начале зимнего периода.

2. колебания между последовательными значениями можно  сгладить скользящими средним. Рассчитаем трехточечные скользящие средние, так как в показателях объема продаж присутствует ежегодная повторяемость выраженная тремя значениями. Для периода январь – апрель 1996 г. значение скользящей средней отсутствует. Для периода май – август 1996 г. значение скользящего среднего найдем как (28+4+40)/3 = 24. для периода сентябрь – декабрь значение скользящего среднего равно (4+40+31)/3 = 25. Остальные значения рассчитываются аналогично. Занесем полученые результаты в таблице

Нанесем на график трехточечные скользящие средние (рис.3). последние можно использовать при прогнозировании направленности тренда после 1999 г.

Таблица 5

Расчет значений трехточечных скользящих средних.

3. из графика (рис.3) видно, что каждый год показатели объема продаж выказывают достаточную стабильность. Колебания в обе стороны относительно линии тренда достаточно постоянны. Таким образом, в данном случае метод сложения наиболее приемлем для определения прогнозных значений объема продаж в каждом периоде 2000 г. выделим сезонную составляющую путем вычитания значений скользящих средних из фактических значений объема продаж. Полученные разности обычно называют отклонениями.

Для периода январь – апрель 1996 г. значение скользящей средней отсутствует, и поэтому первое значение отклонения рассчитывается для следующего периода. В период май-август 1996 г. фактический объем продаж составил - 4, а соответствующие значение скользящего среднего – 24. Далее рассчитывается отклонение = 4-24 = -20.

Аналогично в сентябре-декабре 1996 г. отклонение рассчитывается путем вычитание скользящего среднего из объема продаж, что дает 40-25 = 15. Точно так же рассчитаны и другие значения отклонений, приведены в таблице 6

Таблица 6

Расчет сезонных отклонений

Проведем анализ сезонных колебаний. За период январь - апрель мы имеем следующие значения отклонений 1997 г. - 4,33, 1998 г. – 6 1999 г. – 4,67.

Среднее этих значений позволяет получить простой оценочный показатель сезонных колебаний. Так, сезонное отклонение за январь – апрель рассчитывается следующим образом = (4,33+6+4,67)/3 = 5

Аналогично можно рассчитать сезонных колебаний в другие периоды

Май – август = -18,75

Сентябрь – Декабрь = 13,89

Фактические значения сезонных колебаний необходимо скорректировать с учетом небольшого заданного смещения.

В таблице приведены значение отклонений и средние отклонения в каждом из периодов. Итоговое среднее арифметическое трех средних показателей равняется 5, -18,79, и 13,89 равно 0,05. Итоговое средне должно равняться нулю. Следовательно, чтобы получить ноль, необходимо скорректировать среднее отклонение в каждом из периодов. Это можно сделать вычитая 0,05 из каждого среднего значения. Таким образом, в чистом виде оценочные значения сезонных колебаний выглядят так.

Январь - апрель = 5-0,05 = 4,95

Май – август = -18,75-0,05 = -18,8

Сентябрь – Декабрь = 13,89-0,05 = 13,84

Значение оценочных показателей сезонных отклонений приведены в таблице 7

Таблица 7

Расчет оценочных показателей.

Оценочные показатели тренда можно рассчитать с помощью уравнения регрессии. Уравнение регрессии имеет вид Y = a +b*X? где Y – значение трехточечных скользящих средних, Х – порядковый номер периода. Коэффициенты а и b найдем используя метод наименьших квадратов (МНК)

b = ∑X*Y-n*Xср*Yср/∑X2-X2ср, a = Yср – b*Xср.

Итак в нашей задачи уравнение регрессии имеет следующий вид Y = 29,9+(-0,14)*Х. Получим, следующие показатели тренда в каждом из периодов 2000 г.

Январь - апрель = 29,9+(-0,14)*13 = 28,09

Май – август = 29,9+(-0,14)*14 = 27,95

Сентябрь – Декабрь =29,9+(-0,14)*15 = 27,81

Нанесем оценочные значения тренда на график (рис.4).

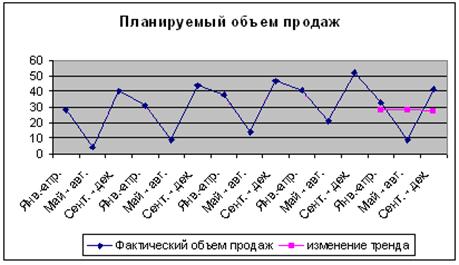
рис. 4 Оценочные значения тренда и прогнозные объемы продаж.

Прогнозные значения можно рассчитать путем сложения оценочных показателей тренда и скорректированных значений сезонных колебаний. Таким образом, мы имеем следующие прогнозные показатели на 2000 г.

Январь – апрель: = 28,09+4,95 =33,04

Май – август = 27,95+(-18,8) = 9,15

Сентябрь – Декабрь = 27,81+13,84 = 41,65

Нанесем полученные данные на график (рис.4)

Отсюда общий объем продаж на 2000 г. составит = 33,04+9,15+41,65 = 83,84 тыс.у.е.

Список литературы

1.     Баликов В.З. Общая экономическая теория. Учебное пособие. – М.: «Издательство ПРИОР», Новосибирск: ООО «Издательство ЮКЭА», 1999 – с. 528

2.     Иохин В.Я. Экономическая теория М.: Юристь, 2003. – 861 с.

3.     Камаева В.Д. Основы экономической теории. - М.: Изд. МГТУ, 1996.

4.     Кролевская Л.П. Банковское дело – 5-е изд., перераб. и доп. – М.: Финансы и статистика, 2003. – с.592 ил.

5.     Куликов П.М. Основы экономической теории: Учебное пособие – М.: Финансы и статистика, 2001 – 400 с.

6.     Николаев И.П. Экономическая теория – М.: «КноРус», 1998. – с.224

7.     Носова С.С. Экономическая теория. – М.: Изд-во. «Дашков и Ко», 2003. – 864с.